Гидравлика Экзамен. 1. Определение гидравлики. Основные понятия и определения. Сплошная среда. Гидравликой

• Название: 1. Определение гидравлики. Основные понятия и определения. Сплошная среда. Гидравликой
• Анкор: Гидравлика Экзамен.doc
• Дата: 26.04.2017
• Размер: 2.14 Mb.
• Имя файла: Гидравлика Экзамен.doc
• Тип: Документы; #5498
• страница: 1 из 4

1. Определение гидравлики. Основные понятия и определения. Сплошная среда.

Гидравликойназывается прикладная наука, занимающаяся изучением законов покоя и движения жидких тел и рассматривающая способы приложения этих законов к решению конкретных технических задач.

Основные понятия и определения гидравлики:

1. 
   Жидкость– физическое тело, обладающее большой подвижностью частиц, которая объясняется слабой связью между молекулами. Поэтому жидкости легко изменяют свою форму, т.е. легко деформируются, не дробясь на части, под действием сил самой незначительной величины или, другими словами, обладают текучестью при приложении к ним незначительных сил сдвига. Жидкость не имеет своей формы, но принимает форму сосуда, в котором она находится.
   

Все жидкости делятся на капельные и газообразные. Таким образом, под это определение попадают и газы, которые, в отличие от жидкостей в общепринятом смысле этого слова (или капельных жидкостей), называются «упругими» жидкостями.

Капельная жидкость имеет объем, и если объем меньше объема сосуда, то жидкость занимает часть объема сосуда и образует свободную поверхность. В отличие от капельных жидкостей газы, как упругие жидкости, не имеют своих определенных формы и объема. Они всегда занимают весь объем сосуда, в котором находятся.

Жидкости отличаются от твердых тел тем, что они обладают такими свойствами, как адгезия, удельный вес, поверхностное натяжение и упругость насыщенного пара.

2)Идеальная жидкость –жидкость, которая не сжимается под действием давления, не изменяет плотности при изменении температуры и не обладает вязкостью.

3) Сплошная среда – жидкость без пустот, разрывов и трещин, диаметр частиц больше длины свободного пробега молекул . Модель сплошной среды позволяет применять для анализа такой мощный математический аппарат, как дифференциальное и интегральное исчисление.

2. Основные физические свойства жидкостей.

1) Плотность ρ- это масса единицы объема жидкости (кг/м³): ρ = m / V.

2) Удельный вес  - называется вес единицы объема этой жидкости (Н/м³):  = G / W

G - вес жидкого тела, [H]; W - объем, [м³].

Между плотностью и удельным весом существует связь:  = ρ∙g

3) Коэффициент объемного сжатия  _w (Па^-1) - это относительное изменение объема жидкости при изменении давления на единицу: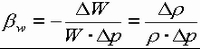



где W - изменение объема W;  - изменение плотности  , соответствующие изменению давления на величину p.

4) Модулем упругости жидкостейE_ж - величина, обратная коэффициенту объемного сжатия (Па): Е_ж=1/ _w ;
5) Коэффициент температурного расширения  _t (⁰С)^-1, выражает относительное изменение объема жидкости при изменении температуры на один градус:  _{t =} W/(W∙t);


6) Вязкость - свойство жидкости оказывать сопротивление перемещению одной части жидкости относительно другой. Вязкость проявляется только при движении жидкости и сказывается на распределении скоростей по живому сечению потока.

В практике для характеристики вязкости жидкости чаще применяют коэффициент динамической вязкости µ, и коэффициент кинематической вязкости  (м²/с). Коэффициентом кинематической вязкости  (м²/с) называется отношение коэффициента динамической вязкости к плотности жидкости:  =µ / ρ. Динамическая вязкость определяется по формуле Пуазейля: µ = (π∙P∙T∙r⁴)/(8∙l∙V).
Вязкость жидкости зависит от рода жидкости, от температуры и от давления.
3. Силы, действующие в жидкости. Гидростатическое давление - определение.

Силы, действующие на жидкость можно разделить на две группы: внутренние и внешние.
Внутренние силы - силы взаимодействия между частицами жидкости.
Внешние силы - силы приложенные к частицам рассматриваемого объёма со стороны других тел. Внешние силы, в свою очередь, делятся на массовые и поверхностные.
Поверхностные силы- приложены к отдельным частицам, находящимся на поверхности раздела. Пропорциональны площади поверхности, на которую действуют. Передаются от частицы к частице без изменения. Например, атмосферное давление, действующее на свободную поверхность, а также силы трения.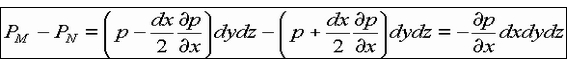


Массовые силы - эти силы действуют на все частицы, рассматриваемого объема, величина сил пропорциональна массе этих частиц. Передаются от частицы к частице, суммируясь.



Гидростатическое давление - это сжимающее напряжение, которое возникает в жидкости находящейся в состоянии относительного покоя.

4. Давление абсолютное, избыточное и вакуумметрическое.

Давление Р_A = Р_B + ρgh называют Абсолютным давлением.

Избыточным давлением называют разницу между абсолютным и атмосферным давлениями:

Р_изб = Р_абс - Р_атм = Р_o + ρgh - Р_атм

Если давление в жидкости меньше атмосферного, то Вакуумметрическим давлением называют величину:

Р_вак = Р_атм - Р_абс
5. Свойства гидростатического давления.

Первое свойство: Гидростатическое давление направлено по внутренней нормали к поверхности, на которую оно действует.
Второе свойство: Гидростатическое давление в точке действует одинаково по всем направлениям и может быть выражено соотношением

Px=Py=Pz=Pn

(2.2)

Третье свойство: Гидростатическое давление в точке зависит от ее координат в пространстве и может быть записано следующим образом:

P=f (x, y, z)

6. Эпюры гидростатического давления.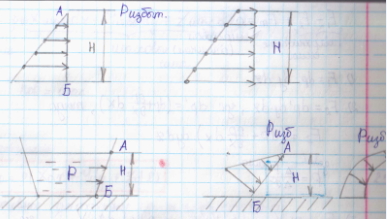




7. Дифференциальные уравнения равновесия жидкости (уравнения Эйлера).
Выделим в жидкости элементарный параллелепипед с ребрами dx, dy, dz, параллельными соответствующим осям координат (рис ниже). Масса жидкости в параллелепипеде равна ρdxdyd. Отбросим жидкость, окружающую параллелепипед, и заменим действие отброшенной жидкости силами. Это будут сжимающие поверхностные силы давления. Кроме поверхностных сил на жидкость действуют массовые силы fdW. Плотность распределения массовых сил f, ее проекции на координатные оси fх, fy, fz.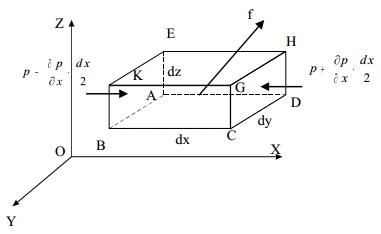



Пусть давление в центре объема равно p. Тогда для давления в центре граней ABKE и DCGH можно соответственно записать: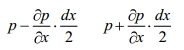



По второму закону Ньютона составим уравнение равновесия параллелепипеда вдоль оси OX: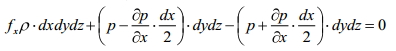



раскрывая скобки и сокращая, получаем: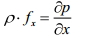



Записывая аналогичные уравнения для осей OY и OZ, получим: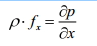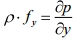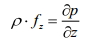



Данные уравнения называются уравнениями равновесия Эйлера.
В ЛЕКЦИЯХ ВОТ ТАКОЕ УРАВНЕНИЕ: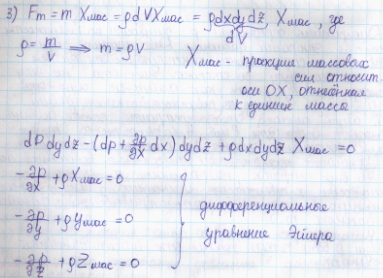


8. Основное дифференциальное уравнение гидростатики.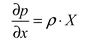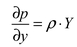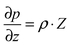


Умножив каждое из уравнений (выше) соответственно на dx, dуи dz и произведя сложение правых и левых частей уравнений, получим: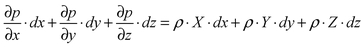



Так как гидростатическое давление p зависит только от трех независимых переменных координат x, y и z, левая часть этого равенства представляет собой полный дифференциал функции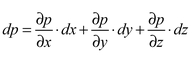



Делая подстановку, находим окончательно: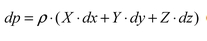



Данное уравнение называется основным дифференциальным уравнением гидростатики, так как его использование позволяет решать основные задачи гидростатики.

9. Основное уравнение гидростатики (закон Паскаля).

Основным уравнением гидростатики (Закон Паскаля) называется уравнение:



— гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,

— плотность жидкости,

— ускорение свободного падения,

— высота точки над плоскостью сравнения (геометрический напор),

— гидростатический напор.

Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.

10 Геометрическое и энергетическое понятия основного уравнения гидростатики.


11. Поверхности равного давления

Поверхность, во всех точках которой значения гидростатического давления равны между собой, называют поверхностью равного давления или поверхностью уровня. На положение уровня свободной поверхности влияют силы тяжести и инерции.

Найдем величину равного давления Р по трем частным производным. При Р=const и р ≠ 0 значение полного дифференциала dP=0 и, следовательно, уравнение поверхности жидкости равного давления имеет вид: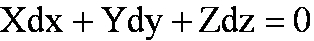



Это уравнение называется уравнением поверхности жидкости равного или постоянного давления. Рассмотрим наиболее часто встречающийся случай.

Когда на покоящуюся жидкость действует одна внешняя сила, сила тяжести, тогда , ,(направление ускорения свободного падения не совпадает с положительным направлением оси Z). В этом случае исходное уравнение имеет вид:


т. е. получаем поверхности равного давления, представляющие собой семейство горизонтальных плоскостей. Каждому значению Z соответствует плоскость, точки которой имеют определенное постоянное значение давления. Свободная поверхность жидкости (для ограниченного объема), в данном случае—одна из плоскостей равного давления. Имеем в виду, что свободная поверхность — это поверхность на границе жидкой и газообразной сред. На свободную поверхность будет приложено постоянное давление равное атмосферному.
12. Относительный покой жидкости

Под относительным покоем понимается такое состояние, при котором в движущейся жидкости отдельные частицы не смещаются одна относительно другой. При этом жидкость перемещается как твердое тело. Само движение жидкости в этом случае можно назвать переносным движением. Для этого состояния характерно постоянство формы объема жидкости. Очевидно, что рассматриваемая масса жидкости будет неподвижна в координатной системе, связанной с движущимся резервуаром.

На жидкость, находящуюся в относительном покое, действуют массовые силы (силы тяжести и силы инерции переносного движения), а из поверхностных — силы давления.

1. Относительный покой при прямолинейном движении на наклонной плоскости

Рассмотрим движение резервуара с жидкостью с постоянным ускорением a по наклонной плоскости, образующей угол a с горизонтальной плоскостью (рис. 3.1).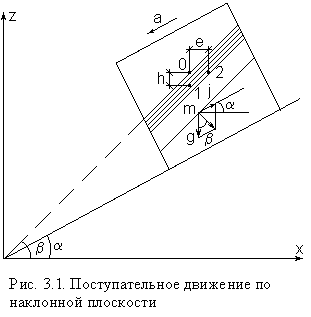



Жидкость в движущемся резервуаре находится под действием силы давления, силы тяжести и силы инерции переносного движения. Ускорение силы инерции j = a и направлено в сторону, обратную ускорению резервуара a. Результирующий вектор массивных сил определяется диагональю параллелограмма, построенного на ускорениях сил тяжести g и инерции j.

Элемент поверхности равного давления перпендикулярен к диагонали параллелограмма и образует с горизонтом угол b , тангенс, которого равен

Таким образом, поверхности равного давления, образуют семейство параллельных плоскостей с углом наклона к горизонту b .

Необходимо учесть, что если резервуар движется равномерно , то и следовательно и . В этом случае поверхности равного давления представляют семейство горизонтальных плоскостей.

Если резервуар перемещается под действием силы тяжести (сила трения резервуара о плоскость равна 0), то , , , а поверхности равного давления образуют семейство плоскостей, параллельных плоскости скатывания.

Если резервуар перемещается с ускорением, но вертикально (), то , а поверхности равного давления образуют семейство горизонтальных плоскостей.

Найдем закон распределения давления в вертикальной плоскости . Учитывая, что система координат перемещается вместе с резервуаром, , а для выбранной плоскости и , уравнение (2.6) примет вид:

. В этом случае Тогда

После интегрирования имеем: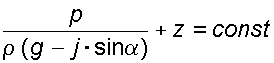

Для двух точек 0 и 1 с координатами и имеем:

или .

По аналогии получаем распределение давления в горизонтальной плоскости:

, если , то имеем ,

а свободная поверхность имеет угол наклона к горизонту

.

При свободном падении резервуара и , то есть во всем объеме давление одинаково.