1. Определение линейных электрических цепей
Электрической цепью называют совокупность соединенных друг с другом источников электрической энергии и нагрузок, по которым может протекать электрический ток. 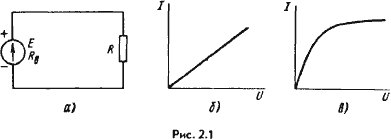
Постоянным током называют ток, неизменный во времени. По-стоянный ток представляет собой направленное упорядоченное движение частиц, несущих электрические заряды.
Изображение электрической цепи с помощью условных знаков называют электрической схемой (рис. 2.1, а). Зависимость тока, протекающего по сопротивлению, от напряжения на этом сопротивлении называют вольт-амперной характеристикой (ВАХ). По оси абсцисс на графике обычно откладывают напряжение, а по оси ординат — ток.
Сопротивления, ВАХ которых являются прямыми линиями (рис. 2.1, б), называют линейными, электрические цепи только с линейными сопротивлениями — линейными электрическими цепями. Сопротивления, ВАХ которых не являются прямыми линиями (рис. 2.1, в), т. е. они нелинейны, называют нелинейными, а электрические цепи с нелинейными сопротивлениями — нелинейными электрическими цепями.
2. Источник ЭДС и источник тока.
Источник ЭДС
Им считается идеальный источник, представляющий собой двухполюсник, на зажимах которого электродвижущая сила (и напряжение) всегда поддерживается постоянным значением. На него не влияет нагрузка сети, а внутреннее сопротивление у источника равно нулю.
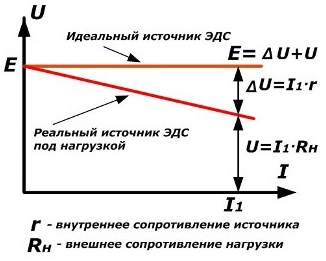 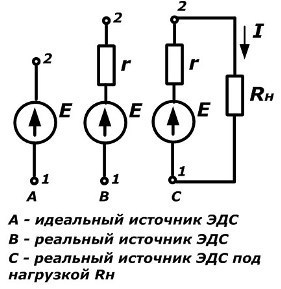
Схемы обозначения и вольт-амперные характеристики источников ЭДС
Теоретически на выводах у идеального источника напряжение не зависит от величины тока нагрузки и является постоянной величиной. У реального источника при увеличении тока нагрузки значение напряжения на зажимах всегда уменьшается.
На графике видно, что ЭДС Е состоит из суммы падений напряжения на внутреннем сопротивлении источника и нагрузке.
В действительности источниками напряжения работают различные химические и гальванические элементы, аккумуляторные батареи, электрические сети. Их разделяют на источники:
постоянного и переменного напряжения;
управляемые напряжением или током.
Источники тока
Ими называют двухполюсники, создающий ток, который является строго постоянной величиной и никак не зависит от значения сопротивления на подключенной нагрузке, а 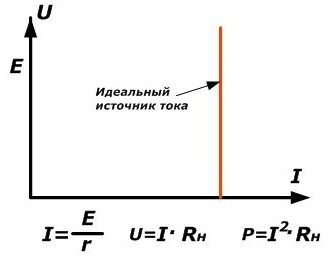 внутреннее сопротивление его приближается к бесконечности. Это тоже теоретическое допущение, которое на практике не может быть достигнуто. внутреннее сопротивление его приближается к бесконечности. Это тоже теоретическое допущение, которое на практике не может быть достигнуто.
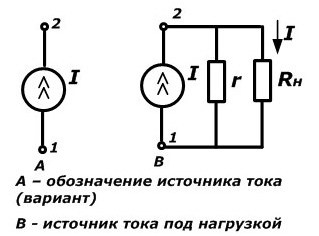
Схемы обозначения и вольт-амперная характеристика источника тока
Для идеального источника тока напряжение на его клеммах и мощность зависят только от сопротивления подключенной внешней схемы. При этом с увеличением сопротивления они возрастают.
Реальный источник тока отличается от идеального значением внутреннего сопротивления.
3.Неразветвленные и разветвленные электрические цепи. Последовательное и параллельное соединения резистивных элементов.
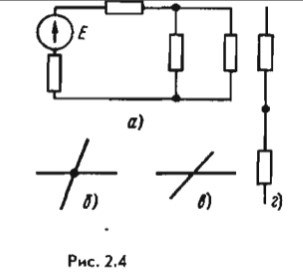
Электрические цепи подразделяют на неразветвленные и разветвленные. На рис. 2.1, а представлена схема простейшей неразветвленной цепи. Во всех элементах ее течет один и тот же ток. Простейшая разветвленная цепь изображена на рис. 2.4, а; в ней имеются три ветви и два узла. В каждой ветви течет свой ток. Ветвь можно определить как участок цепи, образованный последовательно соединенными элементами (через которые течет одинаковый ток) и заключенный между двумя узлами. В свою очередь, узел — это точка цепи, в которой сходятся не менее трех ветвей. Если в месте пересечения двух линий на электрической схеме поставлена точка (рис. 2.4, б), то в этом месте есть электрическое соединение двух линий, в противном случае (рис. 2.4, В) его нет
Последовательное соединение резисторов. При таком соединении по всем элементам последовательной цепи проходит один и тот же ток I. Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR1 + IR2 + IR3 = I(R1 + R2 + R3) = IRэк; Rэк = R1 + R2 + R3.
Напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов:U=U1+U2+U3.
Параллельное соединение резисторов. При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома: I1=U/R1; I2=U/R2; I3=U/R3.
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I1+I2+I3 или
I = U / R1 + U / R2 + U / R3 = U (1/R1 + 1/R2 + 1/R3) = U / Rэк. Эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой: 1/Rэк = 1/R1 + 1/R2 + 1/R3
Эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов: Gэк = G1+ G2 +G3
4. Закон Ома для участка цепи, не содержащего ЭДС. Закон Ома для участка цепи, содержащего ЭДС.
Закон (правило) Ома участка цепи, не содержащего источника ЭДС, устанавливает связь между током и напряжением на этом участке. Применительно к рис. 2.5
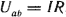 или или 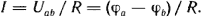
Закон (правило) Ома для участка цепи, содержащего источник ЭДС, позволяет найти ток этого участка по известной разности потенциалов (φа - φс)на концах участка цепи и имеющейся на этом участке ЭДС E.
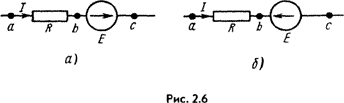
Так, по уравнению (1.2) для схемы рис. 2.6, а
I = (φa - φc + E) / R = (Uac + E) / R;
по уравнению (2.2а) для схемы рис. 2.6, б
I = (φa - φc - E) / R = (Uac - E) / R.
В общем случае
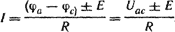 (2.3а) (2.3а)
Уравнение (2.3а) математически выражает закон Ома для участка цепи, содержащего источник ЭДС; знак плюс перед Е соответствует рис. 2.6, а, знак минус - рис. 2.6, б. В частном случае при Е = 0 уравнение (2.3а) переходит в уравнение (2.3).
5. Законы Кирхгофа.
Первый закон Кирхгофа
Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.
Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.
Второй закон Кирхгофа.
Формулировка: 1) алгебраическая сумма падений напряжения в любом замкнутом контуре равна алгебраической сумме ЭДС вдоль того же контура: 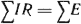 Если направление совпадает с направлением обхода контура «+», иначе «-». Если направление совпадает с направлением обхода контура «+», иначе «-».
2) алгебраическая сумма напряжений (не падений напряжения!) вдоль любого замкнутого контура равна нулю.: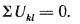
6.Потенциальная диаграмма последовательной электрической цепи.
Под потенциальной диаграммой понимают график распределения потенциала вдоль какого-либо участка цепи или замкнутого контура. По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо произвольной точки, по оси ординат - потенциалы. Каждой точке участка цепи или замкнутого контура соответствует своя точка на потенциальной диаграмме.
7. Электрическая энергия и мощность. Режимы работы элементов электрической цепи.
Электрическая энергия — это способность электромагнитного поля производить работу, преобразовываясь в другие виды энергии.
Электрическая мощность — это работа по перемещению электрических зарядов в единицу времени.
Различают активную, реактивную и полную мощности.
Режимы работы электрической цепи:
Режим холостого хода (т.1) – это режим, при котором сопротивление приемника стремится к бесконечности (RПР = ∞) - на практике это соответствует разрыву электрической цепи, следовательно, ток холостого хода равен нулю (IХ =0).
Номинальный режим (т.2) источника характеризуется тем, что напряжение, ток и мощность его соответствуют тем значениям, на которые он рассчитан заводами- изготовителями.
С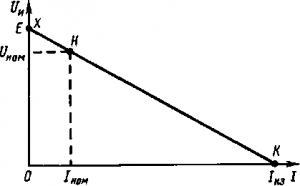 огласованный режим (т.3) - это режим, при котором источник отдает в приемник (во внешнюю цепь) максимальную мощность РMAX. Для достижения данного режима работы источника необходимо подобрать величину сопротивления приемника RПР равным внутреннему сопротивлению источника RВН, то есть RПР = RВН. огласованный режим (т.3) - это режим, при котором источник отдает в приемник (во внешнюю цепь) максимальную мощность РMAX. Для достижения данного режима работы источника необходимо подобрать величину сопротивления приемника RПР равным внутреннему сопротивлению источника RВН, то есть RПР = RВН.
Режим короткого замыкания (т.4) характеризуется тем, что сопротивление приемника становится равным нулю RПР = 0.
8.Метод контурных токов
При расчете методом контурных токов полагают, что в каждом независимом контуре схемы течет свой контурный ток. Уравнения составляют относительно контурных токов, после чего через них определяют токи ветвей.
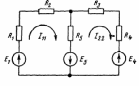 Положим, что в левом контуре по часовой стрелке течет контурный ток I11 а в правой (также по часовой стрелке) — контурный ток I22. Положим, что в левом контуре по часовой стрелке течет контурный ток I11 а в правой (также по часовой стрелке) — контурный ток I22.
Д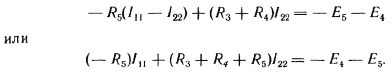 ля второго контура ля второго контура
В уравнении (б) множитель при токе I11, являющийся суммой сопротивлений первого контура, обозначим через R11, множитель при токе I22 (сопротивление смежной ветви, взятое со знаком минус) — через R12.
Перепишем эти уравнения следующим образом:
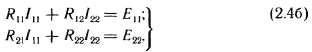

Если в схеме больше двух контуров, например три, то система уравнений выглядит следующим образом:
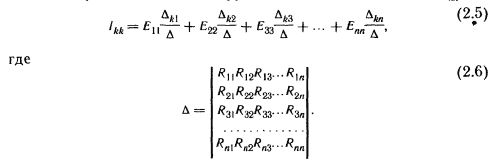 Если в электрической цепи имеется п независимых контуров, то число уравнений тоже равно n. Если в электрической цепи имеется п независимых контуров, то число уравнений тоже равно n.
Общее решение системы n уравнений оносительно тока IKK:
9.Метод узловых потенциалов. Метод двух узлов
Метод узловых потенциалов. Ток в любой ветви схемы можно найти по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов. Допустим, что в схеме n узлов. Так как любая(одна) точка схемы может быть заземлена без изменения токораспределения в ней, один из узлов схемы можно мысленно заземлить, т. е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n - 1. Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по первому закону Кирхгофа.
Метод двух узлов. Часто встречаются схемы, содержащие всего два узла. Наиболее рациональным методом расчета токов в них является метод двух узлов. Под методом двух узлов понимают метод расчета электрических цепей, в котором за искомое (с его помощью определяют затем токи ветвей) принимают напряжение между двумя узлами схемы. напряжение между двумя узлами: 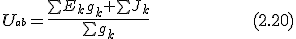 После определения напряжения UаЬ находят ток в любой (n-й) ветви по формуле После определения напряжения UаЬ находят ток в любой (n-й) ветви по формуле 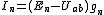
1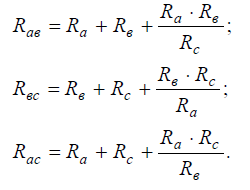 0. Преобразование звезды в треугольник и треугольника в звезду. 0. Преобразование звезды в треугольник и треугольника в звезду.
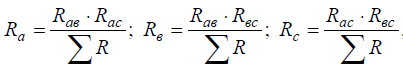 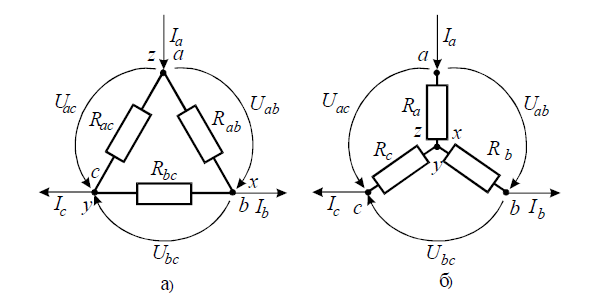

Для упрощения анализа и расчета некоторых электрических цепей, содержащих соединения резисторов треугольником, целесообразно заменить эти резисторы эквивалентными резисторами Ra, Rb ,Rc соединенными звездой.
11. Источники электрической энергии синусоидального тока.
Промышленными источникамисинусоидального тока являются электромеханические генераторы, в которых механическая энергия паровых и гидравлических турбин преобразуется в электрическую.
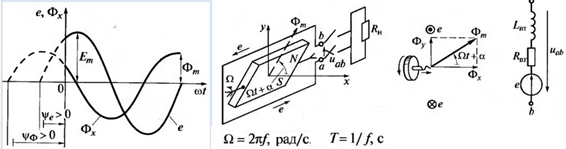
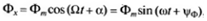 
где Фm – максимальное значение (амплитуда) магнитного потока, пронизывающего виток; a - начальный (т.е. в момент t=0принятый за начало отсчета времени) угол пространственного расположения постоянного магнита относительно оси х; jФ - начальная фаза магнитного потока
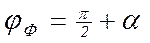 начальная фаза магнитного потока, ; начальная фаза магнитного потока, ;
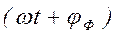 - фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной величины в момент времени t = 0. - фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной величины в момент времени t = 0.
Синусоидальные величины принято изображать графически в виде зависимости 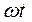 . Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат, т.е. от: . Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат, т.е. от:
Е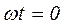 сли начальная фаза >0, то начало синусоидальной величины сдвинуто влево, если <0, то – вправо от начала координат. сли начальная фаза >0, то начало синусоидальной величины сдвинуто влево, если <0, то – вправо от начала координат.
12.Синусоидальный ток и основные величины, характеризующие его
Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону: 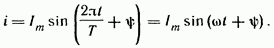 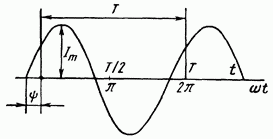
Максимальное значение функции называют амплитудой. Период Т — это время, за которое совершается одно полное колебание. Частота равна числу колебаний в 1 с: 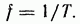 Угловая частота Угловая частота 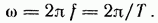 Аргумент синуса, т. е. называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени. Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой. Синусоидальные токи и ЭДС сравнительно низких частот получают с помощью синхронных генераторов. Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов. Аргумент синуса, т. е. называют фазой. Фаза характеризует состояние колебания (числовое значение) в данный момент времени. Любая синусоидально изменяющаяся функция определяется тремя величинами: амплитудой, угловой частотой и начальной фазой. Синусоидальные токи и ЭДС сравнительно низких частот получают с помощью синхронных генераторов. Синусоидальные токи и ЭДС высоких частот получают с помощью ламповых или полупроводниковых генераторов.
13. Максимальное, среднее и действующее значение синусоидальной величины.
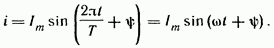 Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону: Синусоидальный ток представляет собой ток, изменяющийся во времени по синусоидальному закону:
Максимальное значение функции называют амплитудой.
Под средним значением синусоидально изменяющейся величины понимают ее среднее значение за половину периода:

Действующее значение тока:
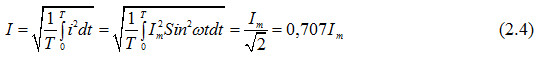
Аналогично U=Um/√2; E=Em/√2.
Под действующим значением синусоидального тока понимают такой ток, который за время, равное периоду, выделяет такое же количество тепла, что и эквивалентный ему постоянный ток.
14. Изображение синусоидально изменяющихся величин векторами на комплексной плоскости.
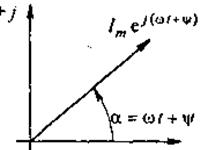
Синусоидально изменяющийся ток :
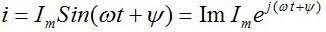
С целью единообразия принято на комплексной плоскости изображать векторы синусоидально изменяющихся величин для момента времени ωt=0. При этом вектор:
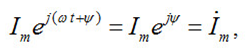
где Ím– комплексная амплитуда, величина, модуль которой равен Im; ψ– угол, под которым вектор Ím проведен к оси +1 на комплексной плоскости, равный начальной фазе.
15.Электрическая цепь переменного тока с последовательным соединением элементов. Комплексное сопротивление.

1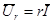 6. Закон Ома в комплексной форме для резистивного, индуктивного и емкостного элементов. 6. Закон Ома в комплексной форме для резистивного, индуктивного и емкостного элементов.
Закон Ома в комплексной форме для резистивного элемента:
Закон Ома в комплексной форме для индуктивного элемента:
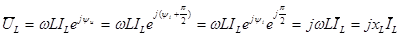
Входящая в полученное выражение величина 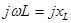 называется комплексным сопротивлением индуктивного элемента, а обратная ей величина называется комплексным сопротивлением индуктивного элемента, а обратная ей величина 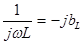 - комплексной проводимостью индуктивного элемента. - комплексной проводимостью индуктивного элемента.
Закон Ома в комплексной форме для емкостного элемента:
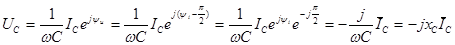
Величина 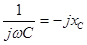 , входящая в выражение (2.30), называется комплексным сопротивлением емкостного элемента, а обратная ей величина , входящая в выражение (2.30), называется комплексным сопротивлением емкостного элемента, а обратная ей величина 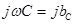 - комплексной проводимостью емкостного элемента. - комплексной проводимостью емкостного элемента.
17. Первый и второй законы Кирхгофа в комплексной форме.
П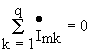 ервый закон Кирхгофа в комплексной форме : Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е. ервый закон Кирхгофа в комплексной форме : Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.
В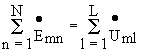 торой закон Кирхгофа в комплексной форме- в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом торой закон Кирхгофа в комплексной форме- в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом
18.Резонанс напряжений
Резонанс в схеме последовательного соединения R, L, С (рис. 3.26, а) называют резонансом напряжений
Р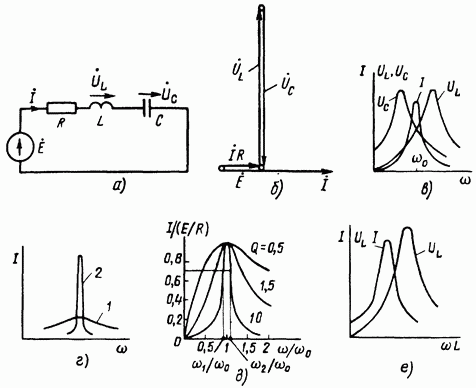 ис. 3.26 ис. 3.26
При резонансе ток в цепи должен совпадать по фазе с ЭДС Е. Это возможно, если входное сопротивление схемы будет чисто активным. Условие наступления резонанса в схеме (рис. 3.26, а) 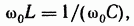
Напряжение на индуктивном элементе при резонансе равно напряжению на емкостном: 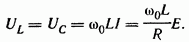 Отношение Отношение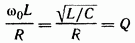 называют добротностью резонансного контура. Добротность показывает, во сколько раз напряжение на индуктивном (емкостном) элементе превышает напряжение на входе схемы в резонансном режиме. называют добротностью резонансного контура. Добротность показывает, во сколько раз напряжение на индуктивном (емкостном) элементе превышает напряжение на входе схемы в резонансном режиме.
19. Резонанс токов.
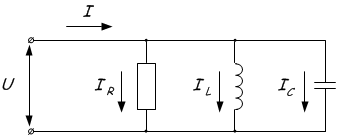 Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором. Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
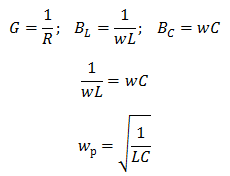 Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны. Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
|
 Скачать 0.93 Mb.
Скачать 0.93 Mb.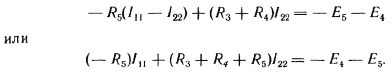 ля второго контура
ля второго контура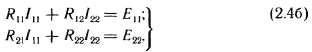
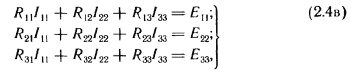
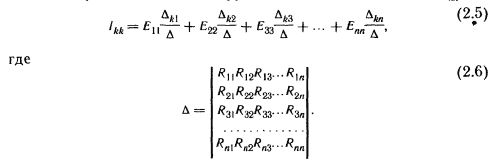 Если в электрической цепи имеется п независимых контуров, то число уравнений тоже равно n.
Если в электрической цепи имеется п независимых контуров, то число уравнений тоже равно n.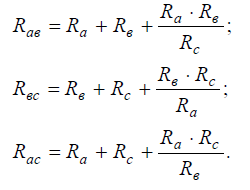 0. Преобразование звезды в треугольник и треугольника в звезду.
0. Преобразование звезды в треугольник и треугольника в звезду.



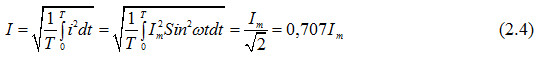

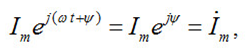

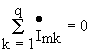 ервый закон Кирхгофа в комплексной форме : Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.
ервый закон Кирхгофа в комплексной форме : Сумма комплексных амплитуд токов ветвей, сходящихся в узле равна нулю, т.е.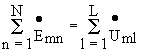 торой закон Кирхгофа в комплексной форме- в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом
торой закон Кирхгофа в комплексной форме- в установившемся синусоидальном режиме сумма комплексных амплитуд ЭДС источников напряжений в контуре равна сумме комплексных амплитуд падений напряжений на элементах контура. Если контур содержит N источников напряжений и L пассивных элементов, то математически это положение формулируется следующим образом ис. 3.26
ис. 3.26 Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.
Резонанс токов возникает в цепи с параллельно соединёнными катушкой резистором и конденсатором.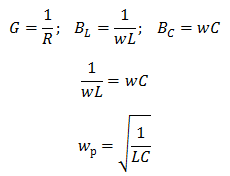 Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.
Условием возникновения резонанса токов является равенство частоты источника резонансной частоте w=wр, следовательно проводимости BL=BC. То есть при резонансе токов, ёмкостная и индуктивная проводимости равны.







 огласованный режим (т.3) - это режим, при котором источник отдает в приемник (во внешнюю цепь) максимальную мощность РMAX. Для достижения данного режима работы источника необходимо подобрать величину сопротивления приемника RПР равным внутреннему сопротивлению источника RВН, то есть RПР = RВН.
огласованный режим (т.3) - это режим, при котором источник отдает в приемник (во внешнюю цепь) максимальную мощность РMAX. Для достижения данного режима работы источника необходимо подобрать величину сопротивления приемника RПР равным внутреннему сопротивлению источника RВН, то есть RПР = RВН. Положим, что в левом контуре по часовой стрелке течет контурный ток I11 а в правой (также по часовой стрелке) — контурный ток I22.
Положим, что в левом контуре по часовой стрелке течет контурный ток I11 а в правой (также по часовой стрелке) — контурный ток I22.