Практика по разработке НГ месторождений. 1. определение показателей разработки залежей при упругом режиме 4
 Скачать 2.71 Mb. Скачать 2.71 Mb.
|
|
Определить изменение контурного давления в течение первых 5.5 лет разработки месторождения, построить график 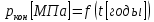 . .РЕШЕНИЕ Изменение давления для упругого режима в неограниченной законтурной области  при радиальной фильтрации воды описывается дифференциальным уравнением в частных производных: при радиальной фильтрации воды описывается дифференциальным уравнением в частных производных: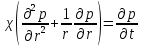 (1.9) (1.9)где 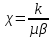 - пьезопроводность пласта. - пьезопроводность пласта.Известно частное решение уравнения (2.1), описывающее изменение давления в зависимости от мгновенного изменения объема жидкости в пласте: 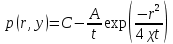 (1.10) (1.10)где С и А – константы интегрирования. С помощью интеграла Дюамеля можно показать, что при переменном во времени отборе воды 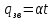 для для 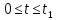 - решение имеет вид: - решение имеет вид: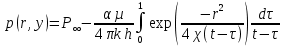 (1.11) (1.11)Для каждого следующего периода 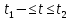 и и 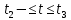 в (1.13) будут появляться соответствующие интегралы, и окончательное решение примет вид [2]: в (1.13) будут появляться соответствующие интегралы, и окончательное решение примет вид [2]: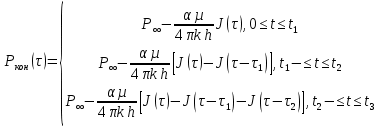 (1.12) (1.12)Здесь 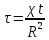 – текущее безразмерное время; – текущее безразмерное время;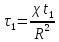 – безразмерное время окончания периода раскуривания месторождения; – безразмерное время окончания периода раскуривания месторождения;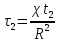 – безразмерное время окончания периода стабилизации отбора жидкости; – безразмерное время окончания периода стабилизации отбора жидкости;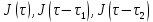 - значения интеграла Дюамеля для времени - значения интеграла Дюамеля для времени 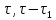 , , 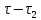 соответственно. соответственно.Для произвольного 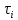 интеграл Дюамеля приближенно вычисляется по формуле: интеграл Дюамеля приближенно вычисляется по формуле: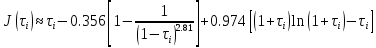 (1.13) (1.13)Пример расчета представлен в таблице 1.3. Определение изменения давления в пласте при упругом режиме В неограниченном продуктивном пласте, насыщенном за контуром нефтеносности водой, обладающей вязкостью примерно равной вязкости нефти пущены в эксплуатацию в различное время 4 добывающие скважины (рис. 1.2). ЗАДАНИЕ 1 Определить как изменится давление в точке А (находящейся на линии расположения скважин 1, 2 на одинаковом расстоянии от них) по сравнению с начальным пластовым давлением спустя время 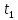 после пуска первой скважины. Исходные данные для расчета приведены в табл. 1.4. после пуска первой скважины. Исходные данные для расчета приведены в табл. 1.4.Таблица 1.3
Образец таблицы для проведения расчётов Таблица расчетных данных
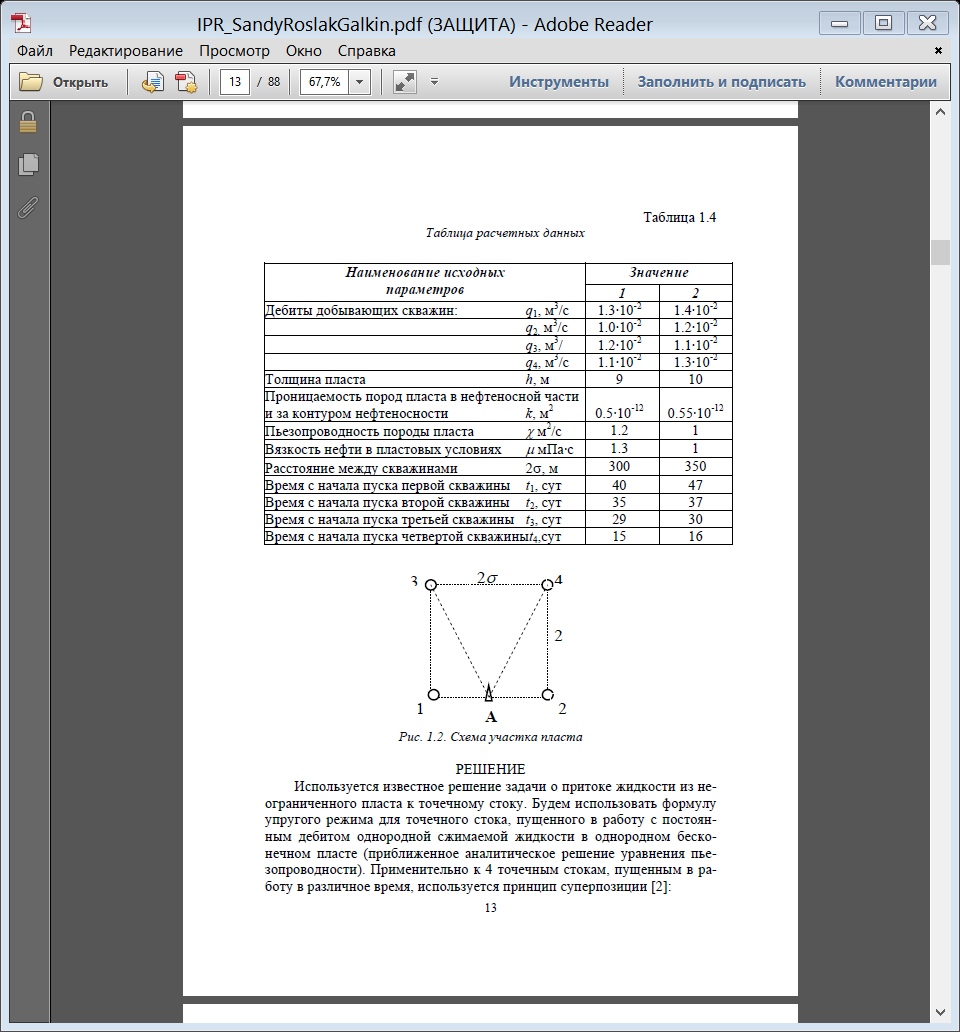 Рис. 1.2. Схема участка пласта РЕШЕНИЕ Используется известное решение задачи о притоке жидкости из неограниченного пласта к точечному стоку. Будем использовать формулу упругого режима для точечного стока, пущенного в работу с постоянным дебитом однородной сжимаемой жидкости в однородном бесконечном пласте (приближенное аналитическое решение уравнения пьезопроводности). Применительно к 4 точечным стокам, пущенным в работу в различное время, используется принцип суперпозиции [2]: 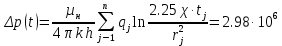 Па (1.4) Па (1.4)Где 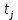 – время с начала пуска скважины номер j; – время с начала пуска скважины номер j;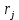 – расстояние от рассматриваемой точки А (в которой определяется изменение давления – расстояние от рассматриваемой точки А (в которой определяется изменение давления ) до скважины номер j; ) до скважины номер j;Рекомендуется использовать размерности физических величин в единой международной системе единиц СИ. ЗАДАНИЕ 2 Для условий предыдущей задачи определить как изменится давление в точке В (рис. 1.3) по сравнению с начальным пластовым давлением спустя время t1 после пуска первой скважины при следующих исходных данных: 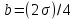 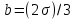 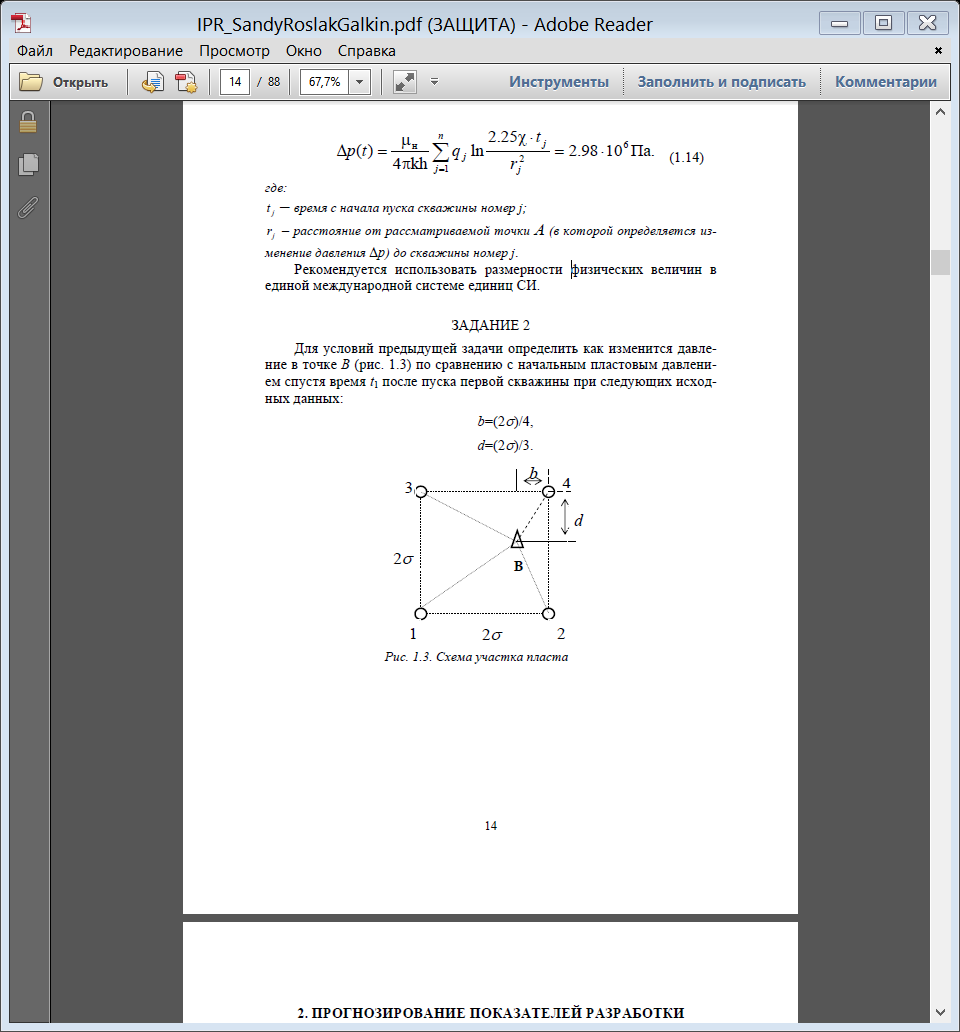 Рис. 1.3. Схема участка пласта | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

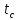
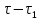
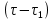
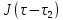
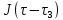 )
)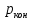 [Па]
[Па] , м3/с
, м3/с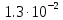
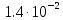
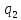 , м3/с
, м3/с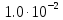
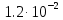
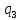 , м3/с
, м3/с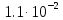
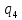 , м3/с
, м3/с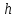 , м
, м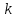 , м2
, м2