Практика по разработке НГ месторождений. 1. определение показателей разработки залежей при упругом режиме 4

• Название: 1. определение показателей разработки залежей при упругом режиме 4
• Дата: 27.10.2022
• Размер: 2.71 Mb.
• Имя файла: Практика по разработке НГ месторождений.docx
• Тип: Закон; #757370
• страница: 6 из 11

Таблица исходных параметров

Продуктивный пласт неоднородный. Его можно представить моделью слоистого пласта, состоящего из тонких гидродинамический изолированных пропластков, абсолютная проницаемость которых меняется в соответствии с законом гамма распределения при значении α=2. Плотность гамма распределения при α=2 имеет вид [1,2]: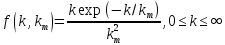

(3.30)

Для нахождения гамма распределения потребуется интеграл: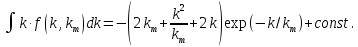

(3.31)

Вытеснение нефти водой из отдельных пропластков происходит по модели поршневого вытеснения, причем во всех пропластках:

• остаточная нефтенасыщенность S_ност постоянна:

• относительная проницаемость k_н для нефти впереди фронта вытеснения постоянна и одинакова для всех пропластков;

• относительная проницаемость k_в для воды позади фронта вытеснения постоянна и одинакова для всех пропластков.

Разработка осуществляется при постоянном перепаде давления Δр между линиями нагнетания и отбора.

Определить для рассматриваемого элемента однорядной системы разработки изменение во времени следующих параметров: q_н(t) - дебита нефти. q_в(t)- дебита воды, B(t) - обводнённой продукции скважин.

РЕШЕНИЕ

Особенность решения данной задачи заключается в том, что в качестве независимого аргумента задается не время, а абсолютная проницаемость полностью обводившегося пропластка k*. По значению к. находится время обводнения пропластка t* и далее остальные параметры.

По условию задачи: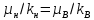



поэтому, упрощенные выражения для дебита нефти и дебита воды для элемента системы разработки будут иметь вид: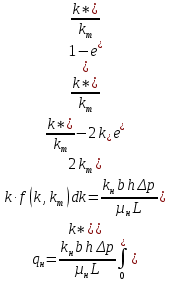

(3.32)

Или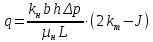

, (3.33)

Где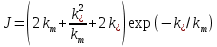

(3.34)

Соответственно для воды: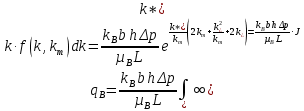

(3.35)

Или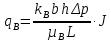

(3.36)

Порядок расчета следующий:

1) Задаемся проницаемостью ободнившегося пропластка (например, в диапазоне от k*=50k_m до k*=k_m/2) и определяем время его обводнения t* по формуле: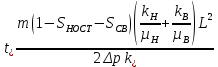

[c] (3.37)

2) По формулам (3.33) н (3.36) вычисляется дебит нефти q_H(t*) и дебит воды в момент времени t*. Расчеты повторяем аналогичным образом для других значении k* (в пределах указанного диапазона). Из (3.36) следует, что чем больше проницаемость обводнявшегося пропластка, тем меньше время его обводнения. Поэтому удобнее задавать k* в порядке убывания, тогда время будет возрастать. Расчеты удобно проводить в таблице 3.9:

Таблица 3.9

Таблица для проведения расчетов

k*/km	k*	t.ceк	t, годы	J	qн	q(м3/сут)	qв	q,(м3/cyт)	В
50
40
30
20
10
5
2
1
0.5

4) Строим зависимости следующего вида (рис. 3.10. рис. 3.11):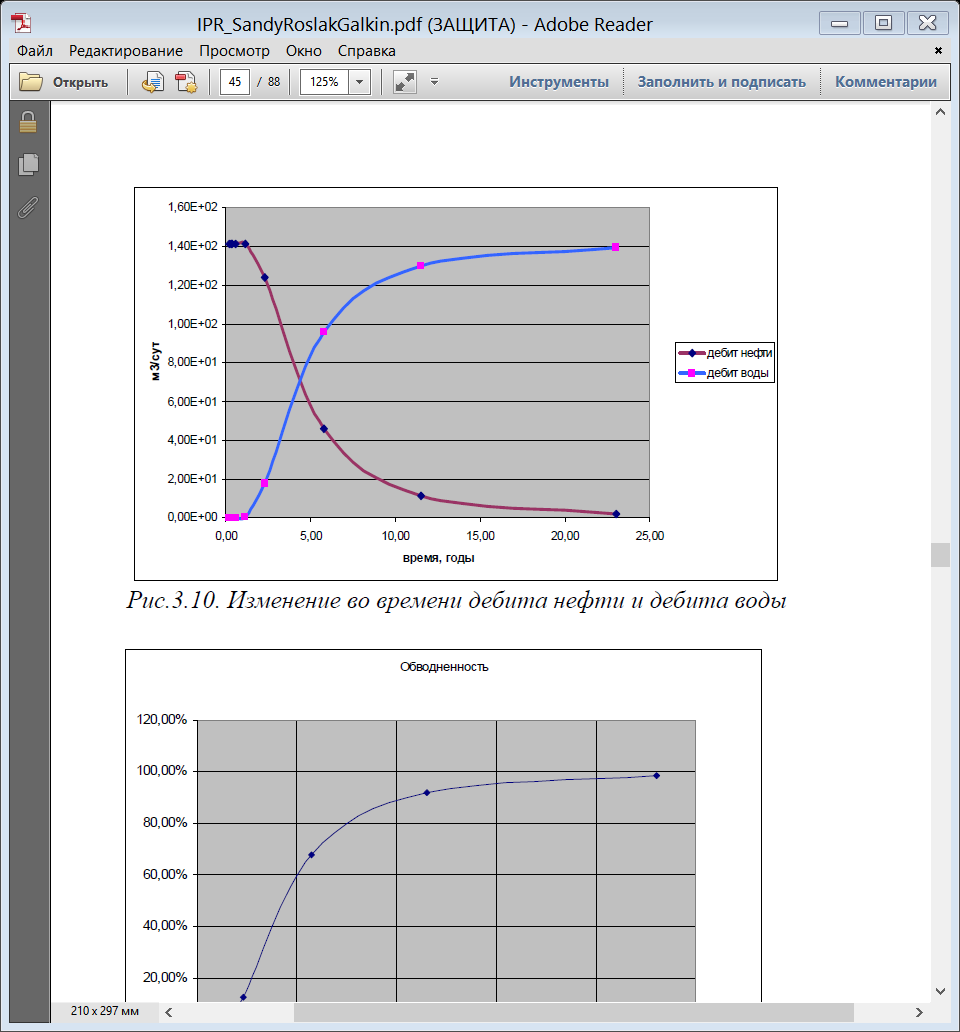



Рис.3.10. Изменение во времени дебита нефти и дебита воды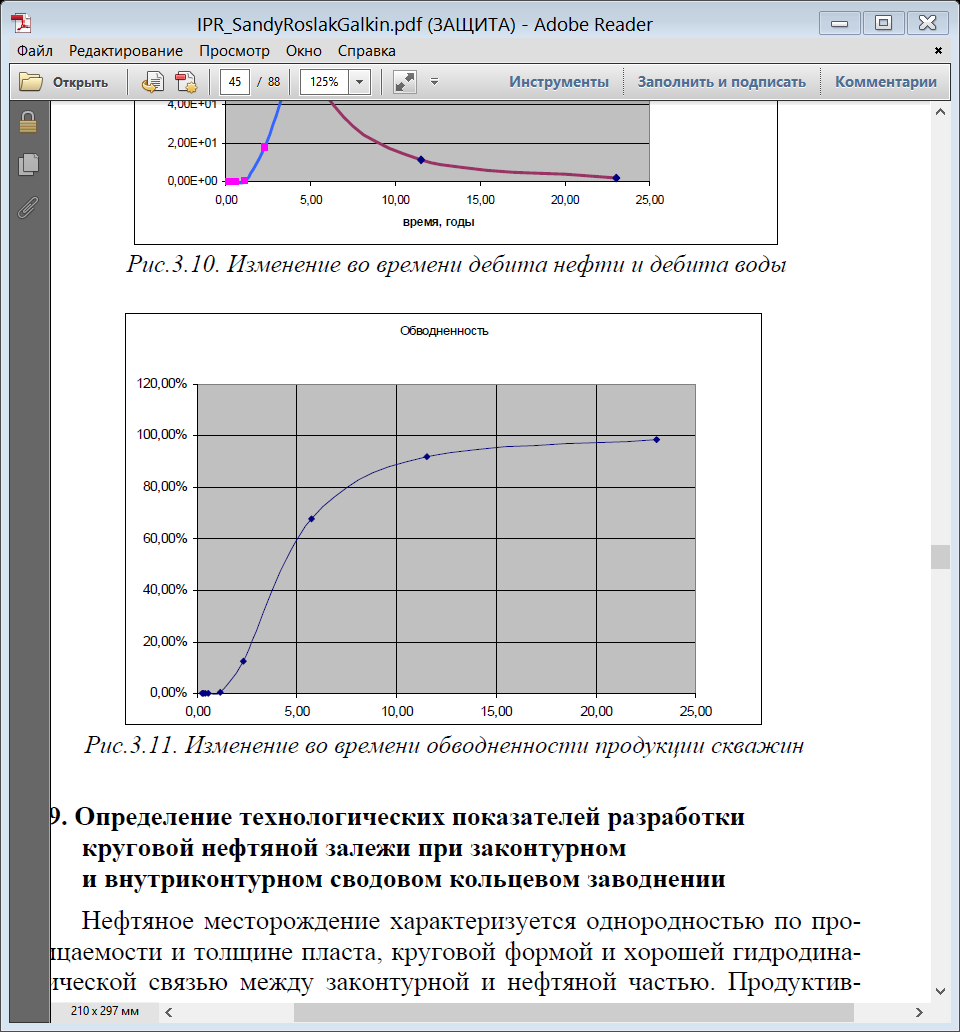



Рис.3.11. Изменение во времени обводненности продукции скважин

9. 
   Определение технологических показателен разработки круговой нефтяной залежи при законтурном н внутриконтурном сводовом кольцевом заводнении
   

Нефтяное месторождение характеризуется однородностью по проницаемости н толщине пласта, круговой формой и хорошей гидродинамической связью между законтурной и нефтяной частью. Продуктивный пласт выклинивается непосредственно за контуром месторождения. При его разработке применяется сводовое кольцевое заводнение в комплексе с законтурным [3]. Схема месторождения, состоящего из одного законтурного ряда и одного кольцевого ряда нагнетательных скважин, и нескольких рядов добывающих скважин (расположенных параллельно кольцевому ряду н внешнему контуру нефтеносности) показана на рнс. 3.12.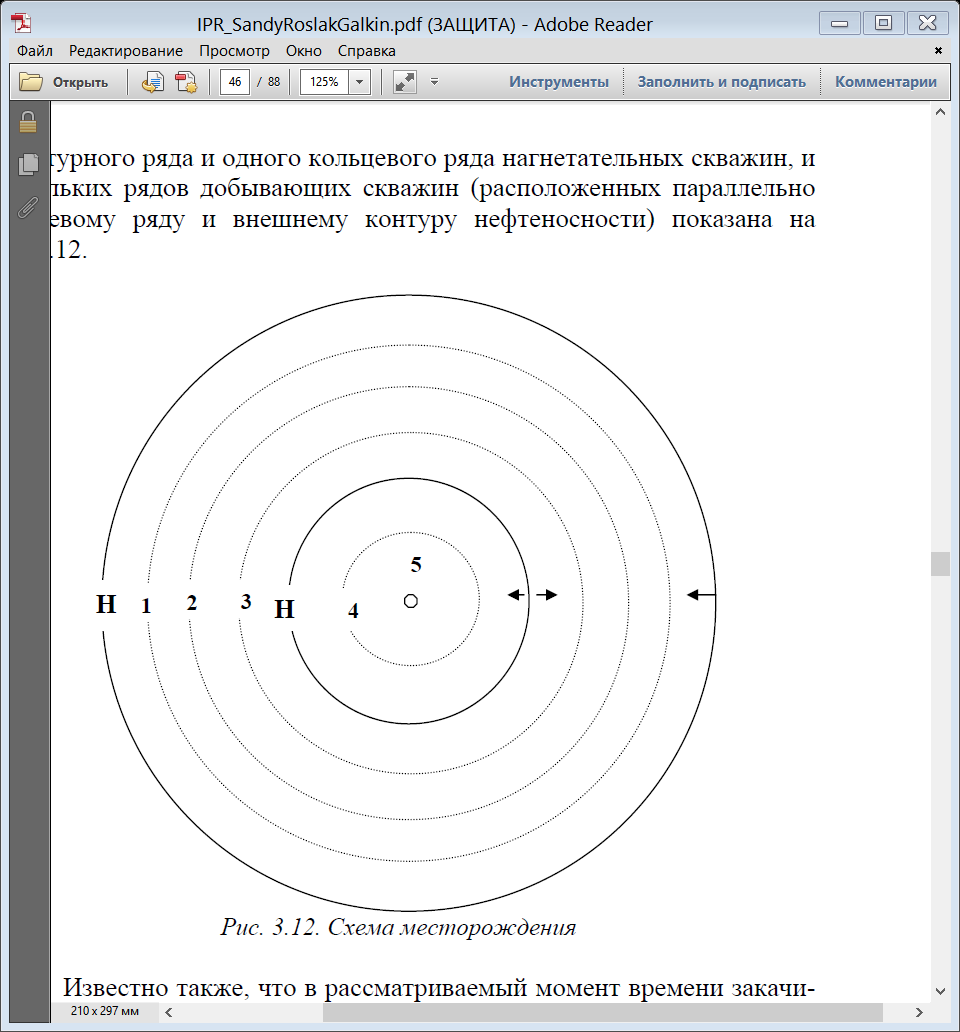



Рис. 3.12. Схема месторождения

Известно также, что в рассматриваемый момент времени закачиваемая вода проникла на расстояние от нагнетательных скважин .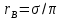

Определить расходы воды, закачиваемой в каждую из нагнетательных скважин законтурного и внутриконтурного ряда, дебиты скважин каждого добывающего ряда.

Исходные данные приведены в табл. 3.10.

Таблица 3.10

Таблица исходных данных для расчета расхода воды и дебитов скважин

Наименование исходных параметров		значение
Радиус внешнего ряда нагнетательных скважин	RНЗ, м	3200
Радиус первого эксплуатационного ряда	R1, м	2800
Радиус второго эксплуатационного ряда	R2, м	2300
Радиус третьего эксплуатационного ряда	R3, м	1800
Радиус кольцевого нагнетательного ряда	RНК, м	1250
Радиус четвертого эксплуатационного ряда	R4, м	700
Расстояние между скважинами в рядах	2𝜎, м	420
Радиус скважины	rc, м	0.1
Толщина пласта	h, м	15
Проницаемость пор пласта для нефти	kН, м2	0.5∙10-12
Проницаемость пор пласта для воды	kВ, м2	0.3∙10-12
Вязкость нефти в пластовых условиях	µН, мПа∙с	2
Вязкость воды в пластовых условиях	µВ, мПа∙с	1
Давление на забоях нагнетательных скважин законтурного
ряда	рНЗ, МПа	19
Давление на забоях нагнетательных скважин кольцевого
ряда нагнетательных скважин	рНК, МПа	18
Давление на забоях добывающих скважин	рЗАБ, МПа	15

РЕШЕНИЕ

Представляем фильтрационную схему пласта для фильтрации воды и нефти эквивалентной ей электрической схемой (рис 3.13):



Рис. 3.13. Схема месторождения. 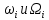, — внешние и внутренние фильтрационные сопротивления

Для расчета расходов воды и дебитов нефти составляем систему уравнений интерференции фильтрационных сопротивлений (используем закон фильтрации Дарси однородной несжимаемой жидкости в пористой среде) путем обхода схемы от p_нз до p₂ , от p_НК до p₂ ,отp_НК доp₅.

Будем иметь в виду, что общий расход воды, закачиваемый в кольцевой ряд нагнетательных скважин (НК) равен q_НК. Однако, будем считать. что влево от этого ряда, в сторону ряда добывающих скважин 3 поступает часть расхода δ₃∙q_нк, а другая часть δ₄∙q_нк – уходит вправо.

Также будем иметь в виду, что часть δ₂₁∙q₂ общего дебита нефти стягивающего ряда 2 обеспечена притоком нефти слева, а другая его часть δ₂₃∙q₂ – притоком справа. Полная система уравнений состоит из трех независимых подсистем и включает в себя следующие уравнения.

3. 
   Уравнения, описывающие фильтрацию воды и нефти на участке пласта от забоев нагнетательных скважин законтурного ряда до забоев добывающих скважин стягивающего ряда:
   

(3.38)

Где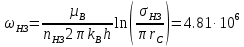

Па∙с/м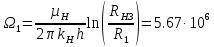³

Па∙с/м³

(3.39)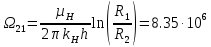

Па∙с/м³

внутреннее и внешнее фильтрационные сопротивления при фильтрации воды и нефти,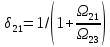

, (3.40)

доля дебита 2-го (стягивающего) ряда добывающих скважин, обеспеченная притоком нефти со стороны 1-го ряда (слева).

3. 
   Уравнения, описывающие фильтрацию воды и нефти на участке пласта от забоев нагнетательных скважин кольцевого ряда до забоев добывающих скважин стягивающего ряда: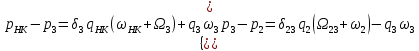
   

(3.41)

где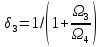

,

доля расхода воды нагнетательного кольцевого ряда, поступающая сторону 3-го ряда добывающих скважин (влево);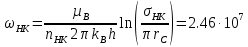

Па∙с/м³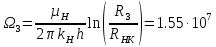

Па∙с/м³

(3.42)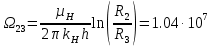

Па∙с/м³

внутренние и внешние фильтрационные сопротивления при фильтрации воды и нефти.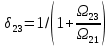

,

доля дебита 2-го (стягивающего) ряда добывающих скважин, обеспеченная притоком нефти со стороны 3-го ряда (справа).

3. 
   Уравнения, описывающие фильтрацию воды и нефти на участке пласта от забоев нагнетательных скважин кольцевого ряда до забоя центральной скважины: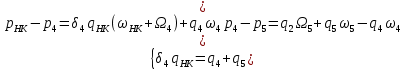
   

(3.43)

Где: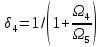

,

доля расхода воды нагнетательного кольцевого ряда, поступающего в сторону 4-го ряда добывающих скважин (вправо);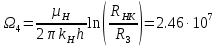

Па∙с/м³

(3.44)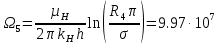

Па∙с/м³

внутренние и внешние фильтрационные сопротивления при фильтрации воды и нефти.

Кроме того, внутренние эквивалентные фильтрационные сопротивления при плоскорадиальной фильтрации нефти к добывающим скважинам /-го ряда определяются выражением: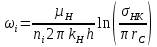

, i=1,…,5 (3.45)

истемы уравнений (3.37, 3.40. 3.42) разрешается относительно неизвестных q₅, q₄, q_НК, q₃, q₂, q₁, q_НЗ,

10.