кинематика. Кинематика плоского движения. Вариант 7. 1. Определение угловой скорости в плоском движении тела
 Скачать 0.96 Mb.
|
|
1. Определение угловой скорости в плоском движении тела. Угловую скорость плоской фигуры при плоском движении можно вычислить, согласно определению, как  Также ее можно определить так:  Величину можно вычислить путем предварительного нахождения скорости какой-либо точки плоской фигуры от вращения фигуры вокруг другой ее точки, принятой за полюс:  , знак угловой скорости определяют по направлению относительной скорости.2. Движение плоской фигуры в её плоскости. Независимость угловых скорости и ускорения тела от выбора полюса. Для доказательства независимости векторов угловой скорости и углового ускорения от выбора полюса, примем за полюса последовательно две различные точки  и  Обозначим  и векторы угловых скоростей вращения тела вокруг мгновенных осей, проходящих через эти полюса (Рис. 6.5). Пользуясь формулой (6.3), выразим скорость произвольной точки М через скорости полюсов  и  Выразим теперь скорость второго полюса  из-за скорости  первого полюса Тут  - радиус-вектор полюса  относительно полюса  Приравнивая правые части равенств (6.6) и, учитывая (6.7), получим 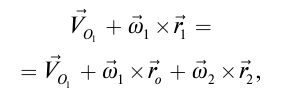 или 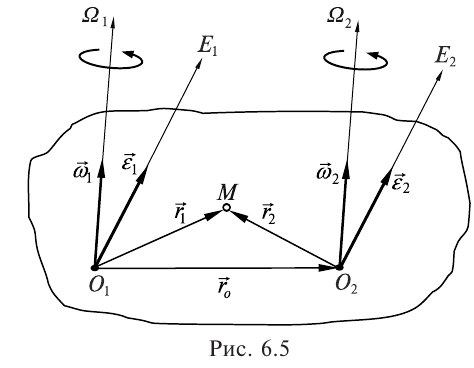  Поскольку  то получим Это равенство справедливо для любого значения  то есть для произвольной точки М, а потому Итак, вектор угловой скорости твердого тела не зависит от выбора полюса. Дифференцируя по времени равенство (6.8), получим 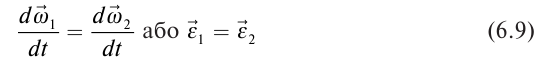 то есть, вектор углового ускорения твердого тела тоже не зависит от выбора полюса. 3. Диск катится без скольжения по неподвижной плоскости, в точке А к диску шарнирно прикреплен стержень АВ. В данном положении механизма определить ускорение ползуна В. Дано: υС = 2 м/с = const r = 0,2 м АB = 0,8 м 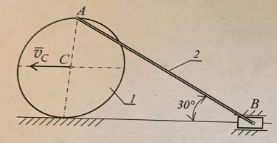 Решение 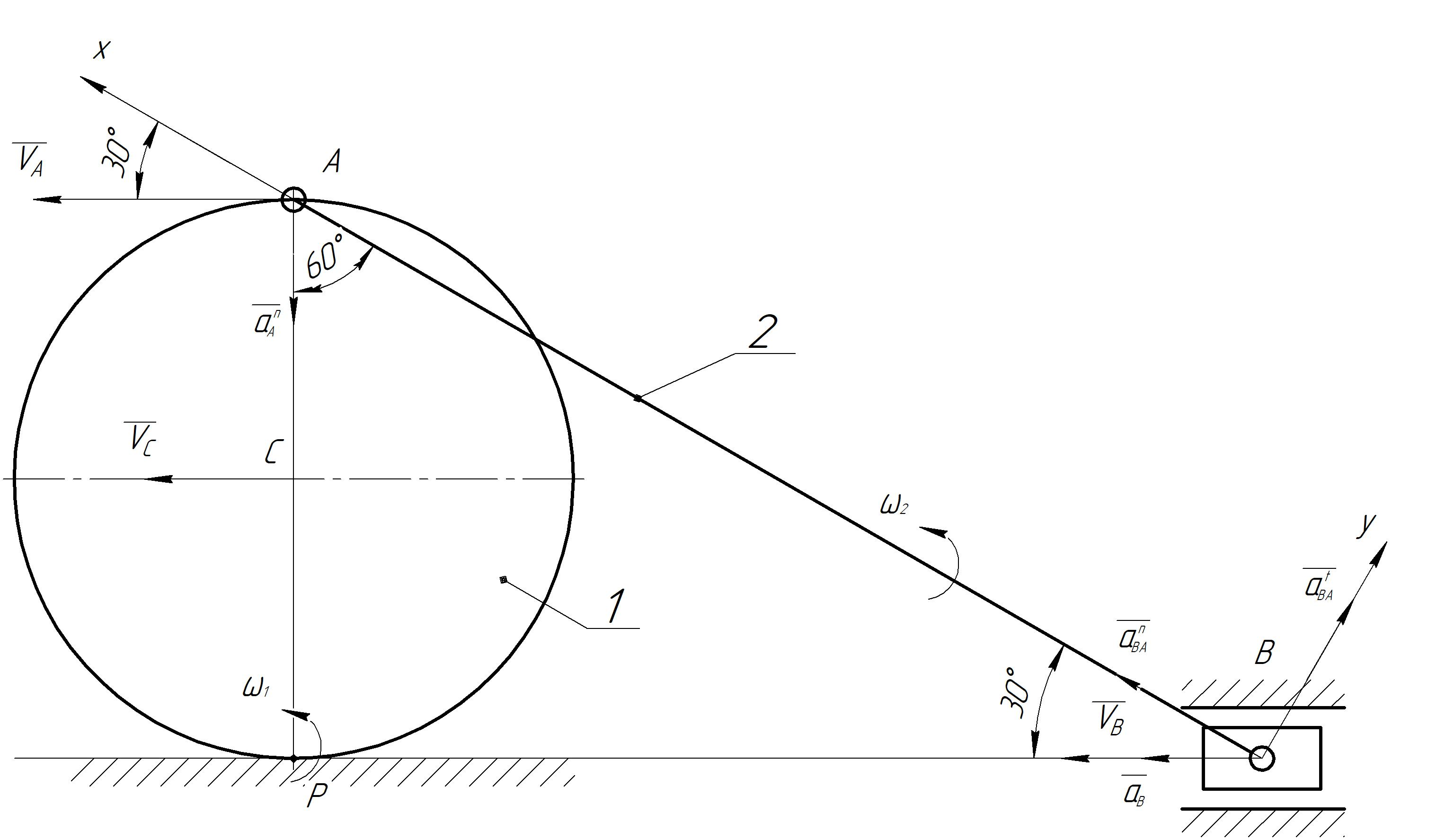 МЦС диска находится в точке Р (точка касания с плоскостью). Проведем отрезок из точки А в точку Р, а от него перпендикуляр и получим вектор скорости точки А. Чтобы найти υА определим угловую скорость диска 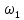 . 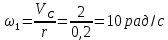Определяем υА. 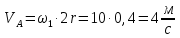 Направление υB || плоскости. Проецируем векторы скоростей точек А и В на прямую АВ и получаем 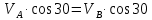 Отсюда 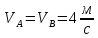 Это значит, что МЦС находится в бесконечности, а угловая скорость звена 2 равна нулю. Ускорение точки А. 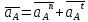 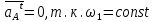 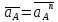 Ускорение точки В. 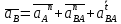 Нормальные ускорения равны: 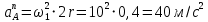 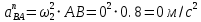 Спроецируем ускорения на ось X и определим ускорение точки В: 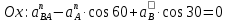 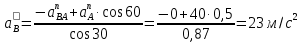 Ответ: 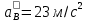 4. В кривошипно-ползунном механизме кривошип 1 вращается с постоянной угловой скоростью 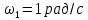 . В заданном положении механизма определить ускорение ползуна 3 и угловое ускорение шатуна 2.Дано: 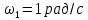ОА = 0,2 м АВ = 0,4 м 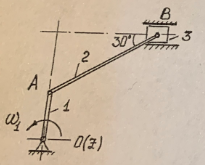 Решение 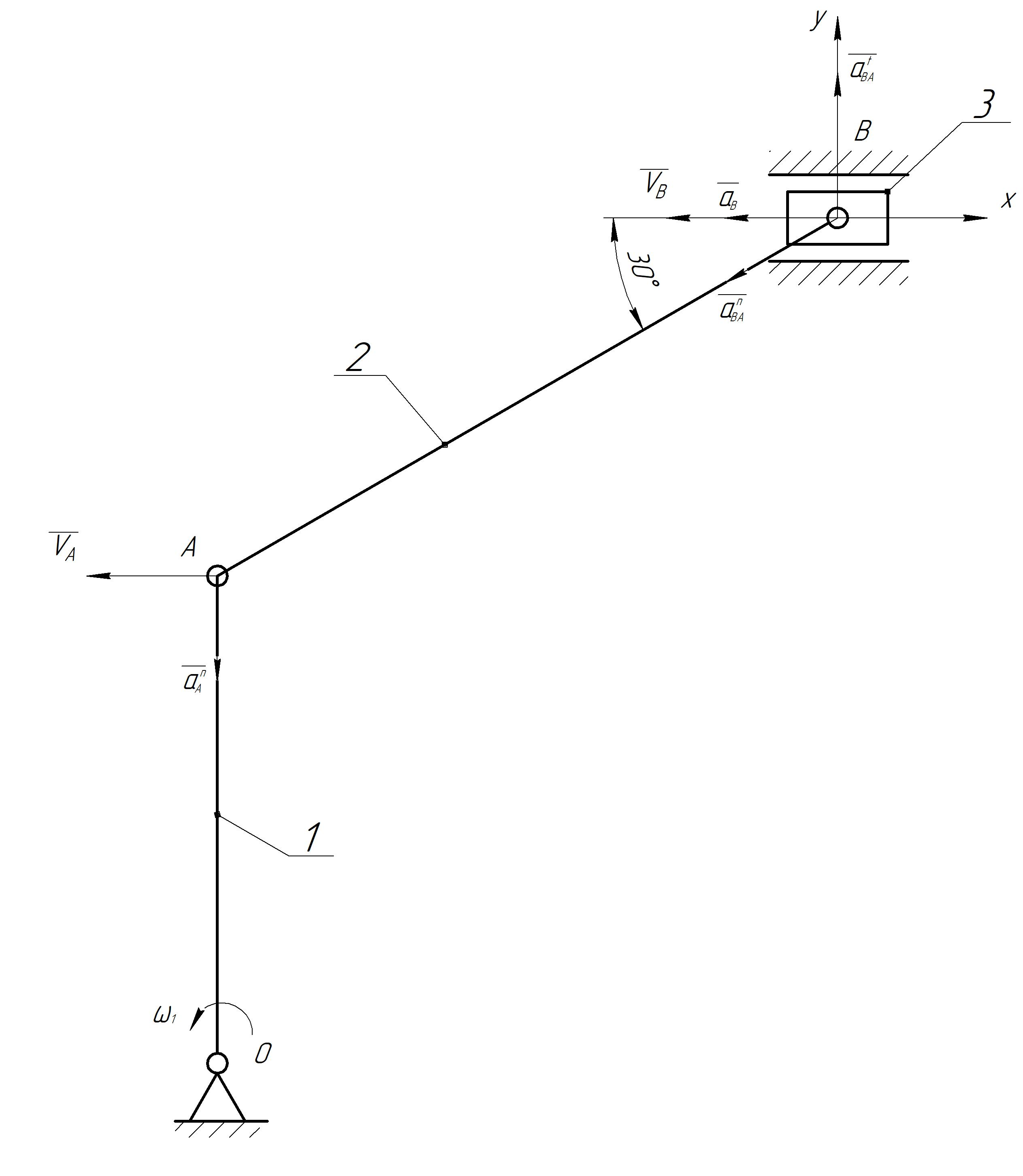 Определим скорость точки А. 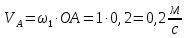 Она направлена перпендикулярно кривошипу 1 в сторону углового ускорения. Проведем вектор скорости точки В (вдоль направляющей). Т.к. вектора скорости точки А и В параллельны, то 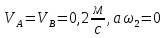 .Ускорение точки А. 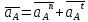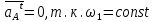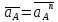Ускорение точки В. 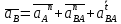Нормальные ускорения равны: 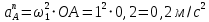 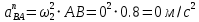 Спроецируем ускорения на оси X и Y и определим ускорение точки В: 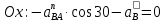 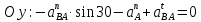 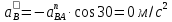 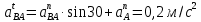 Угловое ускорение шатуна 2: 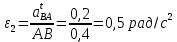 Ответ: 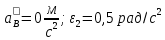 |