Кристал. 1. Определите понятия однородность, анизотропия, симметрия
 Скачать 184.1 Kb. Скачать 184.1 Kb.
|
|
Домашнее задание №2 Вариант №8 1. Определите понятия «однородность», «анизотропия», «симметрия». Ответ: Однородность - тело, каждой точке которого соответствует бесчисленное множество расположенных на конечных расстояниях друг от друга эквивалентных точек не только в физическом, но и в геометрическом смысле. Анизотропия – ориентационная зависимость свойства: зависимость от направления n, вдоль которого это свойство проявляется. Симметрия - инвариантность структуры объекта по отношению к некоторым преобразованиям в пространстве переменных, описывающих рассматриваемый объект. Термин «симметрия» происходит от греческого слова symmetria – соразмерность. 2. Докажите, что у параллелограмма точка пересечения диагоналей является центром симметрии. Ответ:  Рис.1. Параллелограм ABCD. Диагонали параллелограммам (рис.1) в точке пересечения делятся пополам, а значит, при симметрии относительно центра О вершины параллелограмма отобразятся на противоположной вершине этого же параллелограмма. При симметрии отрезок отображается на отрезок, поэтому и стороны параллелограммам отобразятся на противоположные стороны, а значит параллелограмм отобразится сам на себя, т.е. О-центр симметрии. Что и требовалось доказать. 3. Перечислите этапы построения стереографической проекции Ответ: Примем некоторую точку О за центр проекций (рис.2) 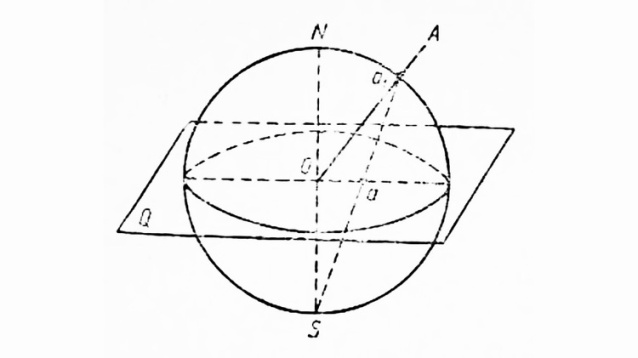 Рис.2 Построение шара прекции. Произвольным радиусом опишем вокруг О шар, называющейся шаром проекций. Через ту же точку О проведём горизонтальную плоскость Q, являющуюся плоскостью проекций. В результате пересечения сферической поверхности с Q имеем большой круг (линии пересечения поверхности шара с плоскостями, проходящими через его центр), отвечающий экватору шара проекций и представляющий круг проекций. Вертикальный диаметр шара NS, перпендикулярный к Q, называется осью проекций. Такая ось пересекает шар проекций в двух точках – N и S.Одна из этих точек (южный полюс шара проекций – S) является точкой зрения. Если требуется изобразить стереографическую проекцию какого-либо направления или плоскости, переносим их параллельно самим себе так, чтобы они прошли через центр О.Рассмотрим получение стереографической проекции некоторого направления ОА (рис.25). Для этого продолжим данное направление до пересечения с поверхностью шара проекций. Пусть точка а1 представляет собой результат пересечения ОА с шаровой поверхностью. Соединим точку а1с точкой зрения S лучом зрения S а1. Точка а- точка пересечения S а1 с плоскостью Q –является стереографической проекцией направления ОА. Таким образом, стереографические проекции направлений изображаются точками. Найдём стереографическую проекцию плоскости R. Предварительно перенесём R параллельно самой себе в центр проекций, продолжим её до пересечения с поверхностью шара проекций (рис.3).  Рис. 3 Стереографическая проекция плоскости R В результате пересечения получим на шаре дугу большого круга а1в1d1… Все точки этой окружности соединяем лучами зренияSа1Sв1Sd1c точкой зрения S. Указанные лучи образуют проектирующий конус с вершиной S. Результат пересечения проектирующего конуса с плоскостью проекций Q соответствует стереографической проекции заданной плоскости. Известна теорема, согласно которой стереографическая проекция круга является также кругом. Таким образом, дуга большого круга а1в1d1… даёт на стереографической проекции дугу окружностиа в d. В общем случае, стереографические проекции плоскостей изображаются круговыми дугами. Перейдём к проектированию кристаллов методом стереографических проекций. Пусть задан некоторый кристаллический многогранник. Примем какую-либо точку О внутри него, например центр тяжести, за центр проекций (рис.4). Из этой точки произвольным радиусом опишем сферическую поверхность – шар проекций. Через центр проведём горизонтальную плоскость проекций Q и условимся весь чертёж изображать на ней. Опустим из центра О на все грани кристалла перпендикуляры и продолжим их до пересечения с поверхностью сферы. В результате пересечений на сферической поверхности возникнет ряд точек. Например, на рис. 4, а нормаль к грани А даёт на шаровой поверхности точку а1.  Рис. 4 Проектирование кристалла методом стереографических проекций (а); изображение проекций граней А, В, С и D на плоскости Q (б) Все найденные точки следует перенести на горизонтальную плоскость проекций Q . С этой целью южный полюс шара S принимаем за точку зрения и соединяем с ней лучами зрения точки, расположенные на сфере. В результате пересечения лучей зрения с плоскостью чертежа получим новые точки, отвечающие стереографическим проекциям нормалей к граням. Таким образом, грани на данной проекции изображаются точками (точка а – стереографическая проекция нормали к грани А (рис.4). Нормали, пересекающие шар проекций в нижней полусфере, проектируются вне этого круга (например, нормаль ОВ на рис.4). Неудобство последнего построения заставляет переносить для таких нормалей точку зрения S в северный полюс сферы N. В этом случае и проекции нижних граней окажутся внутри круга проекций. Чтобы отличить друг от друга проекции нормалей к верхним и нижним граням, первые обозначаются кружками, а вторые – крестиками. Необходимо запомнить: 1. горизонтальные грани проектируются в центре круга проекций (например, грань С, рис.4); 2. вертикальные грани проектируются на самом круге проекций (например, грань D); 3. косые грани проектируются внутри круга проекций (например, грани А и В). Чем круче наклон грани (т.е.чем меньше угол между гранью и осью проекций), тем ближе проектирующая её точка располагается к кругу проекций. И, чем положе грань(чем больше указанный угол), тем ближе соответственная точка к центру круга. 4. Почему в кристаллах гексагональной сингонии вводится дополнительный индекс для обозначения символа грани? Ответ: Четвертый индекс i в символах граней гексагональных кристаллов оказывается удобен, поскольку после его изъятия получим трехиндексовые гексагональные символы, по которым достаточно сложно определить принадлежность граней к одной простой форме. 5. Укажите интервалы изменения сферических координат в сферической проекции кристалла. Ответ: ρ - полярное расстояние, рассчитываемое по любому направлению от нуля («северный» полюс) до 180 градусов; ϕ - долгота, отсчитываемая по экватору от меридиана, принятого за нулевой меридиан, от нуля до 360 градусов. 6. Найдите плотность кристалла неона (при 20 К), если известно, что его решётка – гранецентрированная, кубической сингонии. Постоянная этой решётки при температуре 20 К равна 0,452 нм. Молярная масса неона равна 20 г/моль. Ответ:  |
