Раздел 7 ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
7/1 Функция нескольких переменных
I ЭЛЕМЕНТЫ ТОПОЛОГИИ В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
Топология – раздел математики, изучающий топологические свойства фигур, т. е. свойства, не изменяющиеся при любых деформациях, производимых без разрывов и склеиваний, точнее, при взаимно однозначных и непрерывных отображениях. Топологическое пространство представляет собой множество произвольных элементов, называемых точками, и характеризуемых отношением «бесконечной близости».
ОПР. 1 Множество всевозможных упорядоченных совокупностей n действительных чисел называется n – мерным координатным пространством 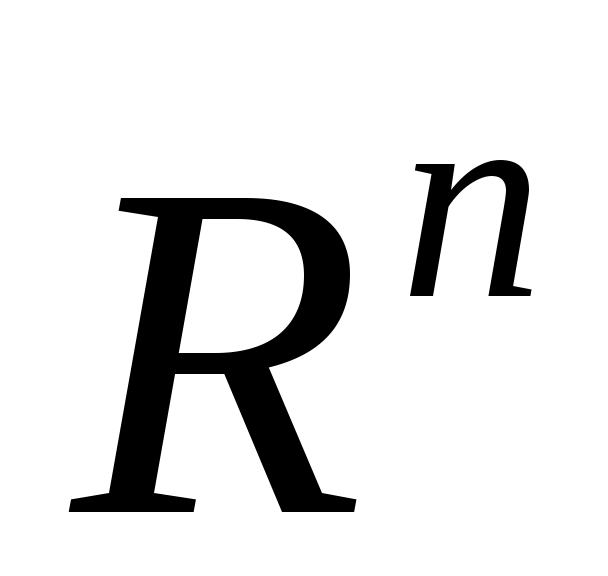 . Каждая такая упорядоченная совокупность, обозначаемая . Каждая такая упорядоченная совокупность, обозначаемая 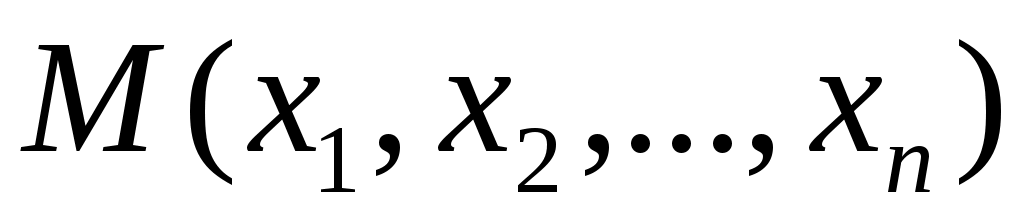 , называется точкой этого пространства, а числа , называется точкой этого пространства, а числа 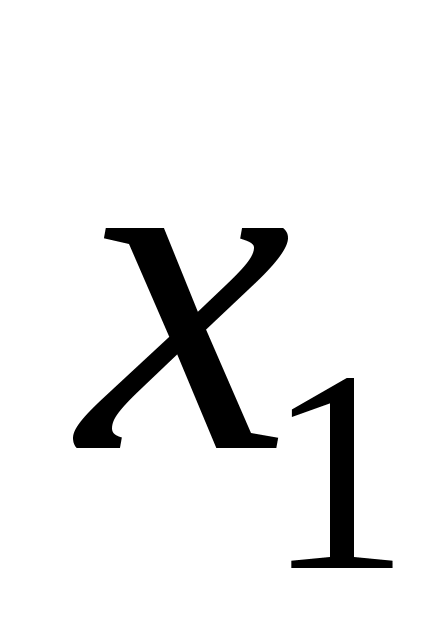 , , 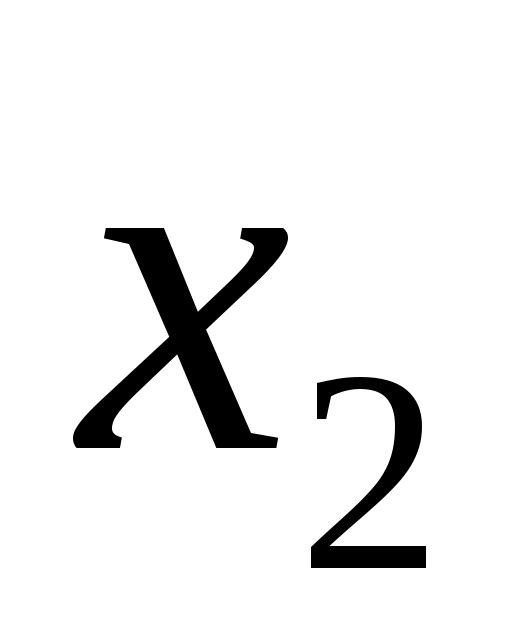 , …, , …, 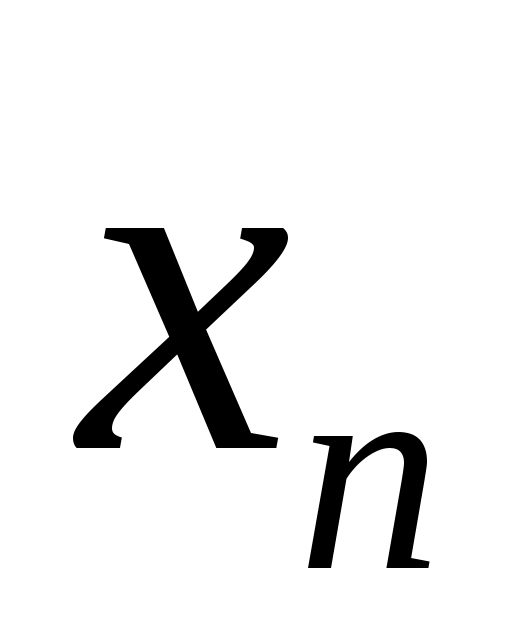 – координатами точки М. – координатами точки М.
Координатное пространство будет n – мерным евклидовым пространством (чаще всего обозначаемым 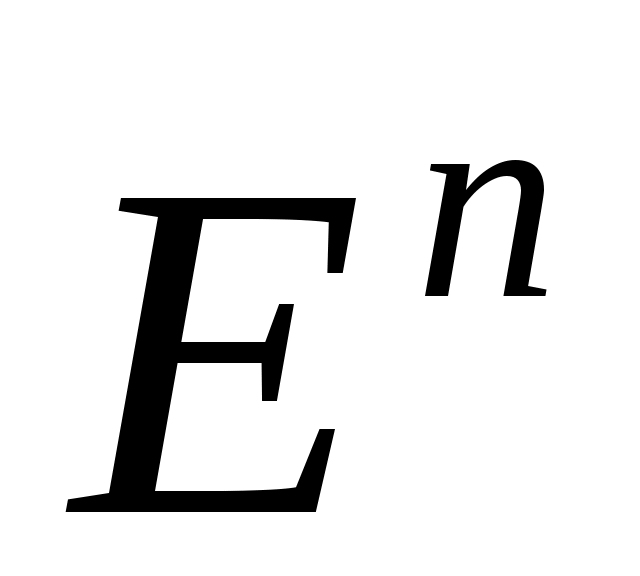 ), если расстояние между двумя его произвольными точками ), если расстояние между двумя его произвольными точками 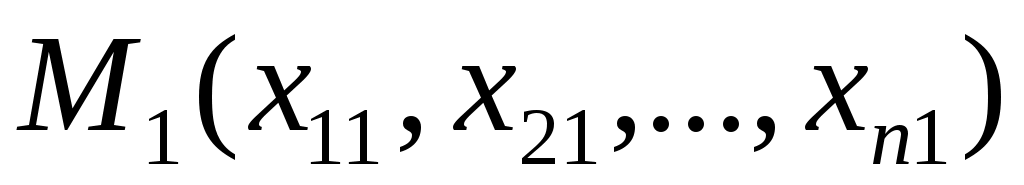 и и 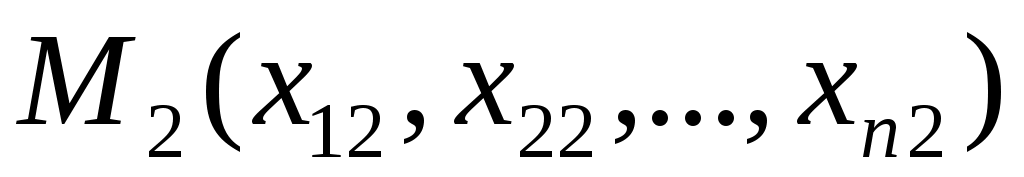 определить по формуле определить по формуле
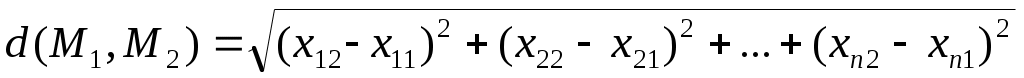 . 1 . 1
Замечание.
Очевидно, что геометрическими образами евклидовых пространств 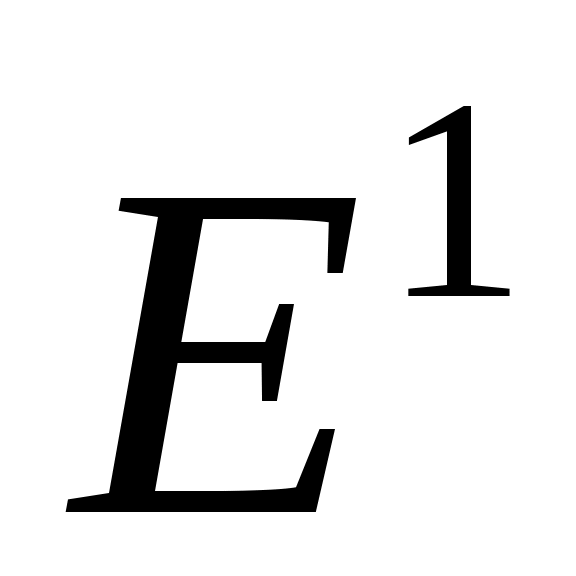 , , 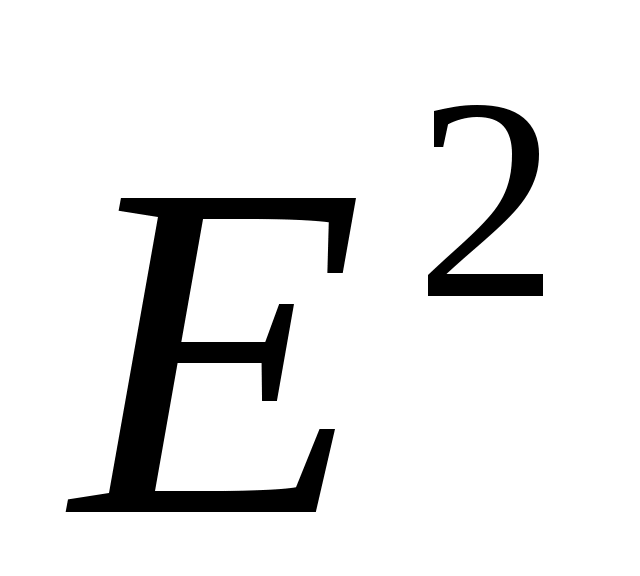 , , 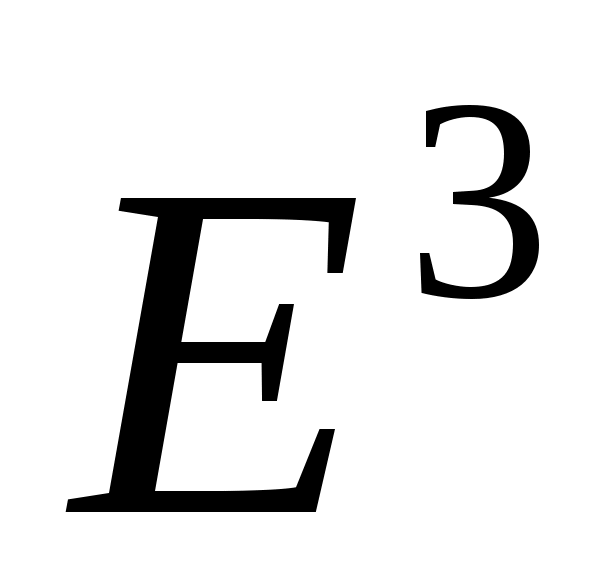 могут служить соответственно координатная прямая, плоскость и трехмерное пространство, в которых введены прямоугольные системы координат, а расстояние в каждом из этих пространств вычисляется, согласно, формуле 1: могут служить соответственно координатная прямая, плоскость и трехмерное пространство, в которых введены прямоугольные системы координат, а расстояние в каждом из этих пространств вычисляется, согласно, формуле 1:
если 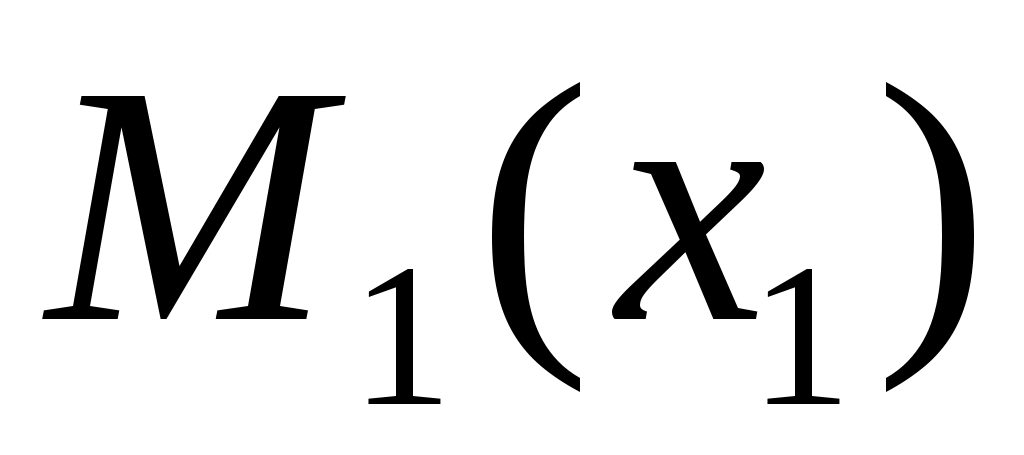 , , 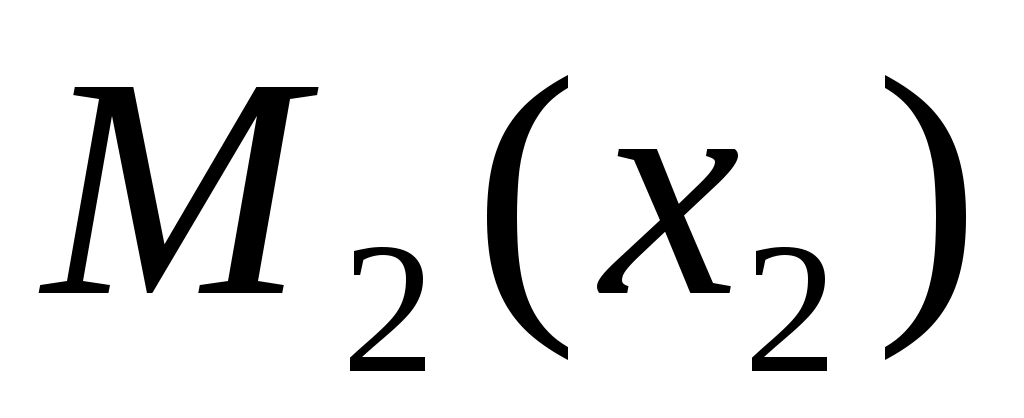 – точки – точки 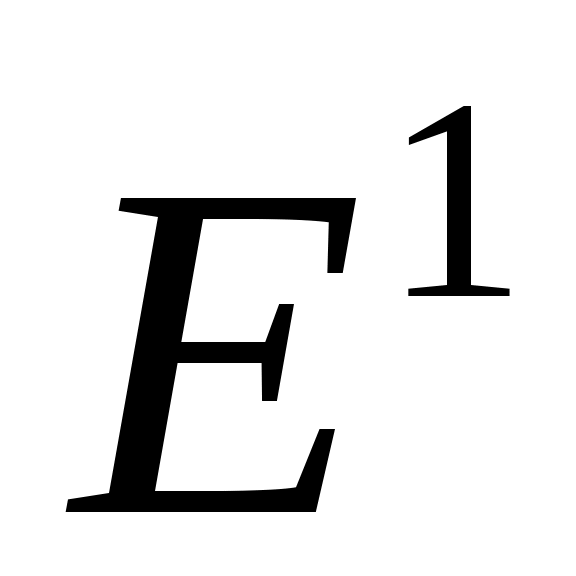 , то , то 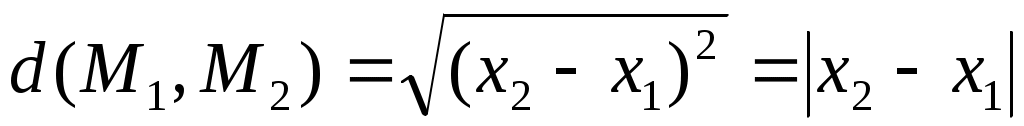 ; ;
если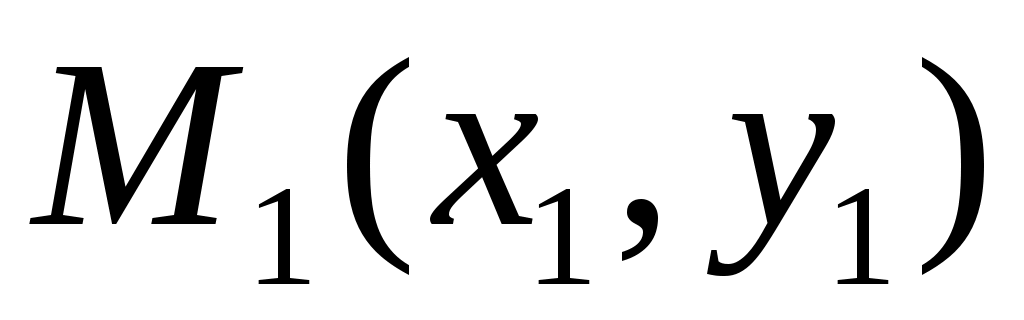 , , 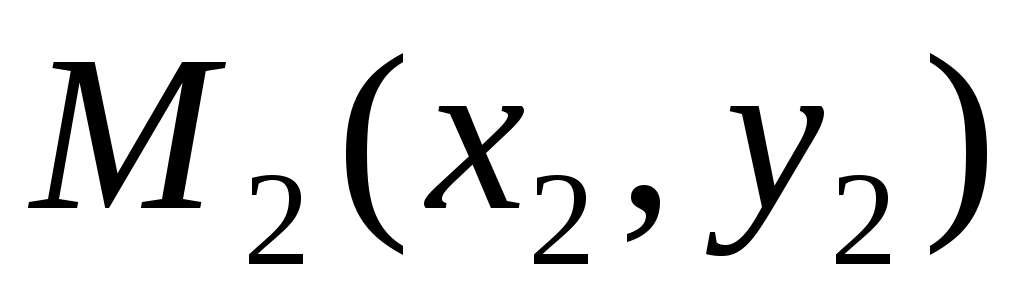 – точки – точки 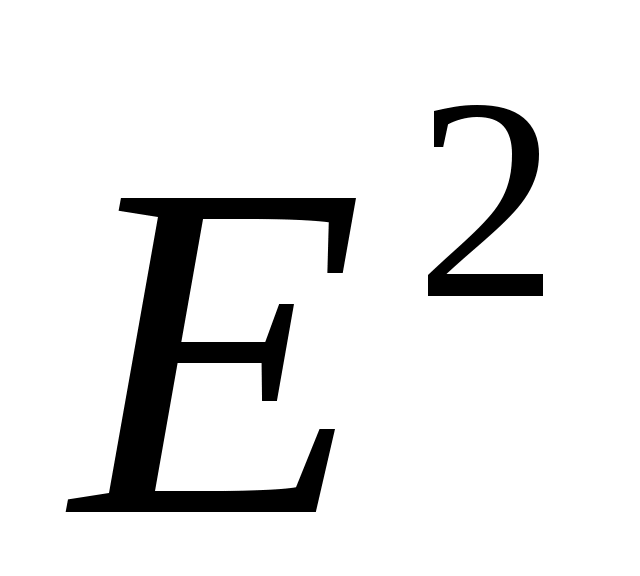 , то , то
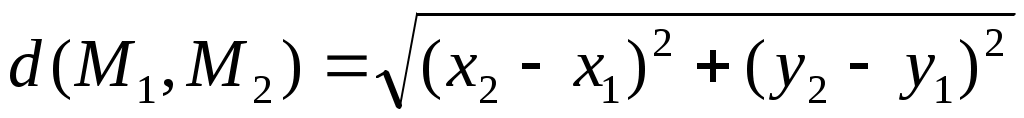 ; ;
если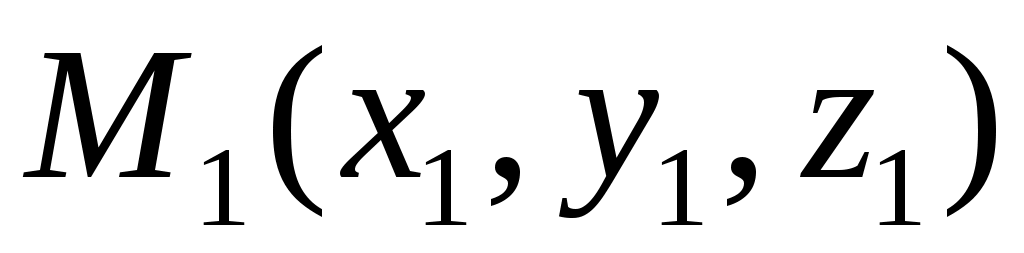 , ,  – точки – точки 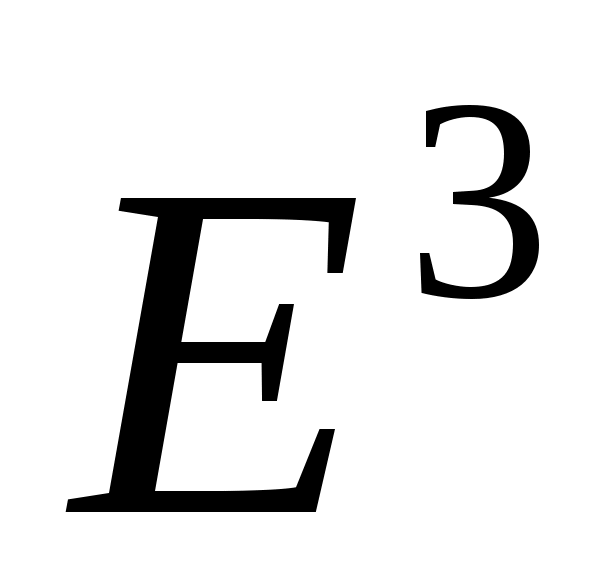 , то , то
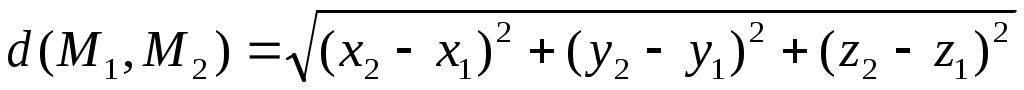 ; ;
таким образом, получены известные формулы из аналитической геометрии.
Рассмотрим классификацию множеств, состоящих их точек n – мерного евклидова пространства 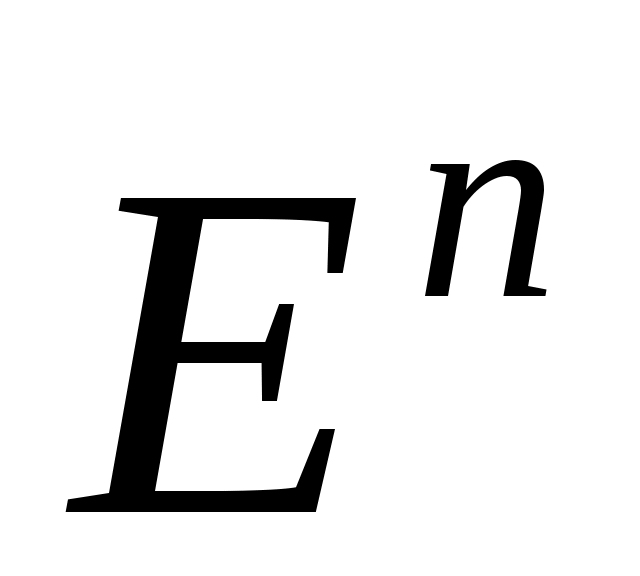 . Пусть даны точки . Пусть даны точки 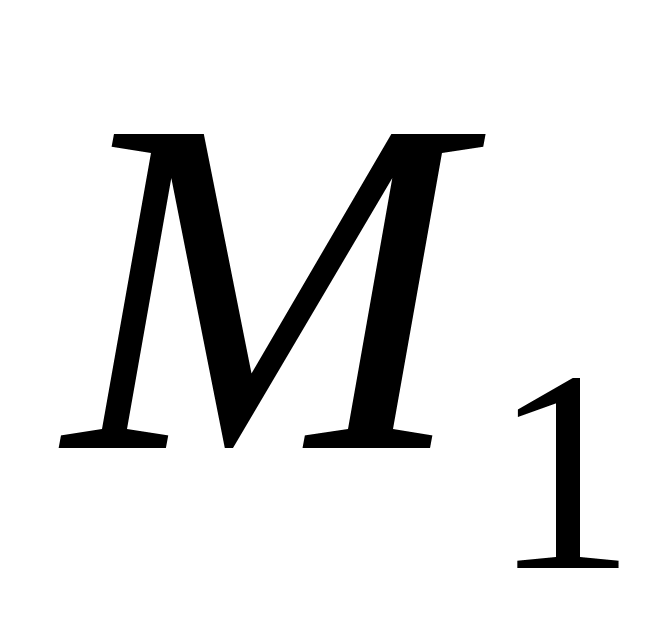 и и 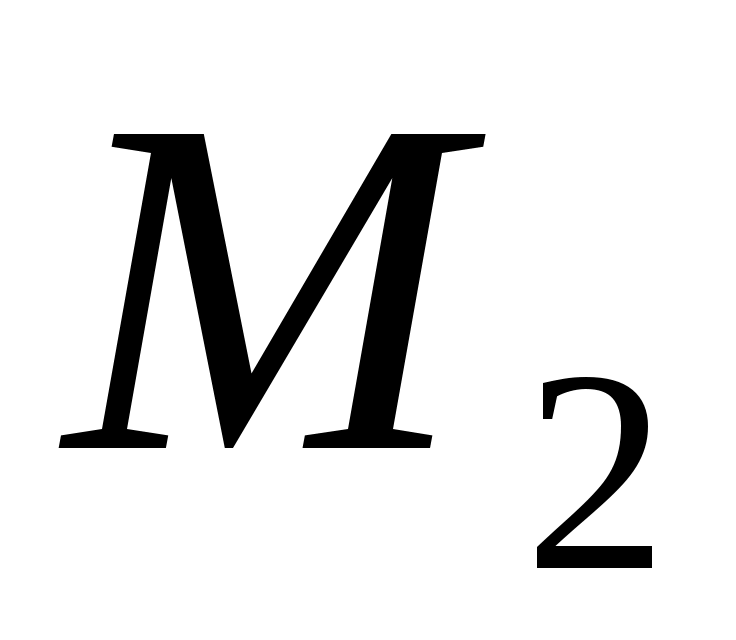 . .
ОПР. 2 Множество всех точек 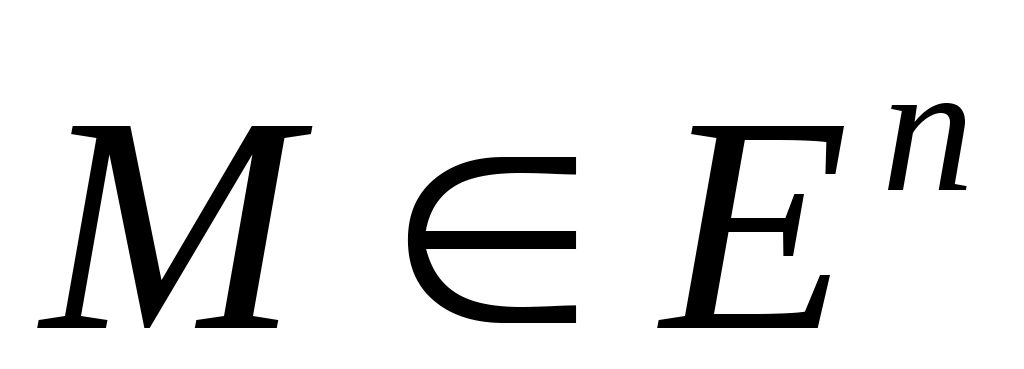 , удовлетворяющих условию , удовлетворяющих условию
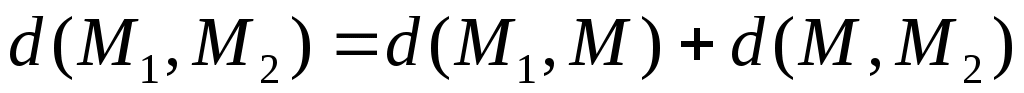 , 2 , 2
называется n – мерным отрезком с границами 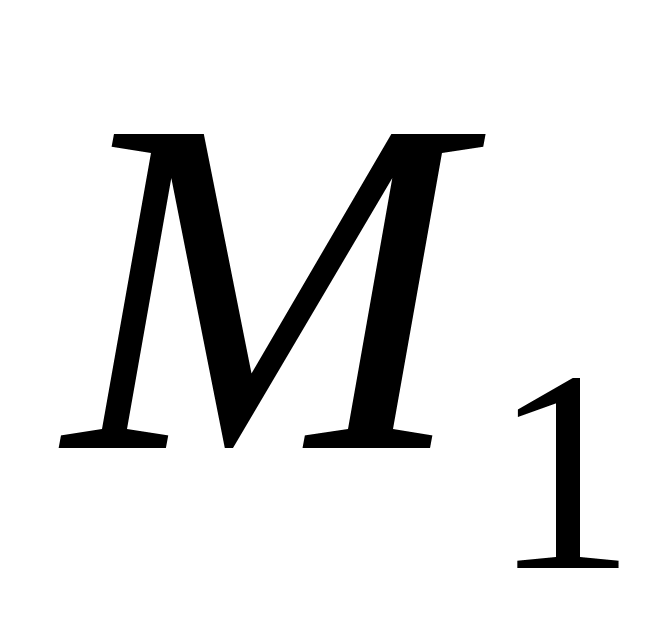 и и 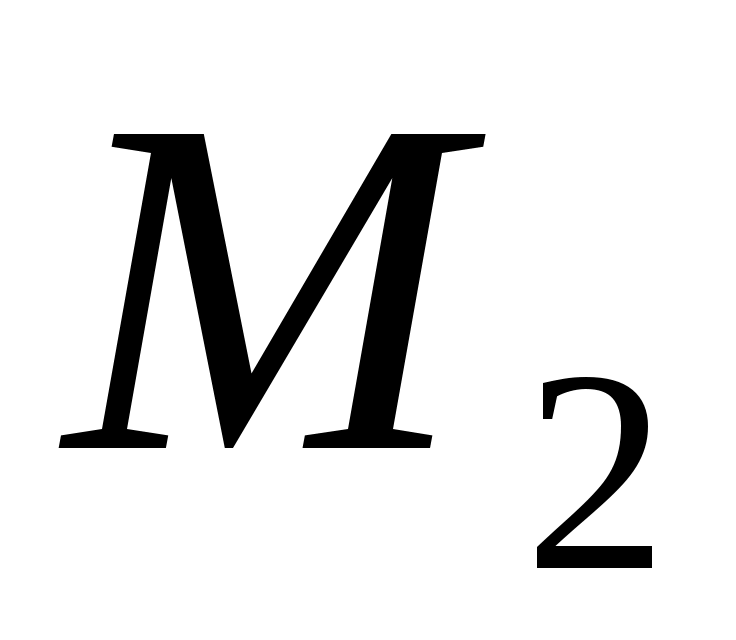 , обозначаемым , обозначаемым 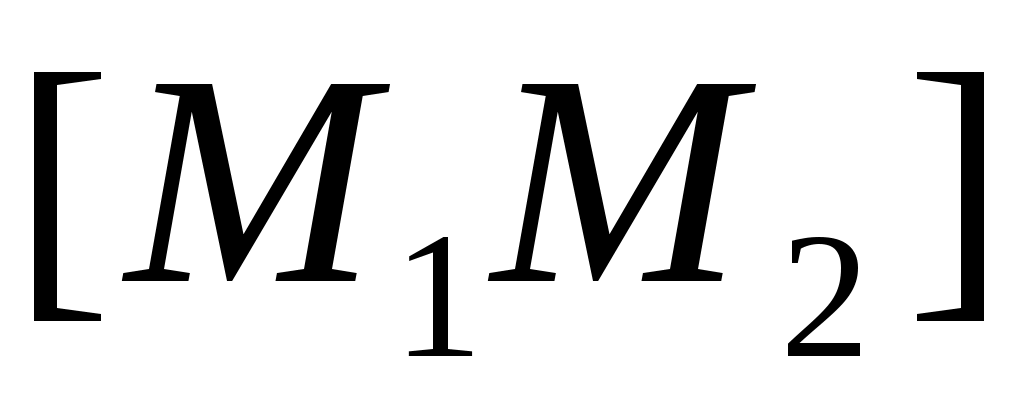 . .
Объединение отрезков 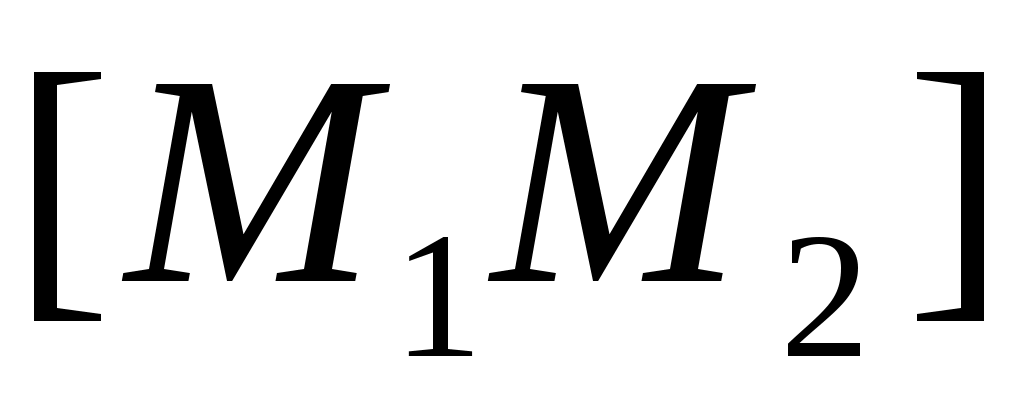 , , 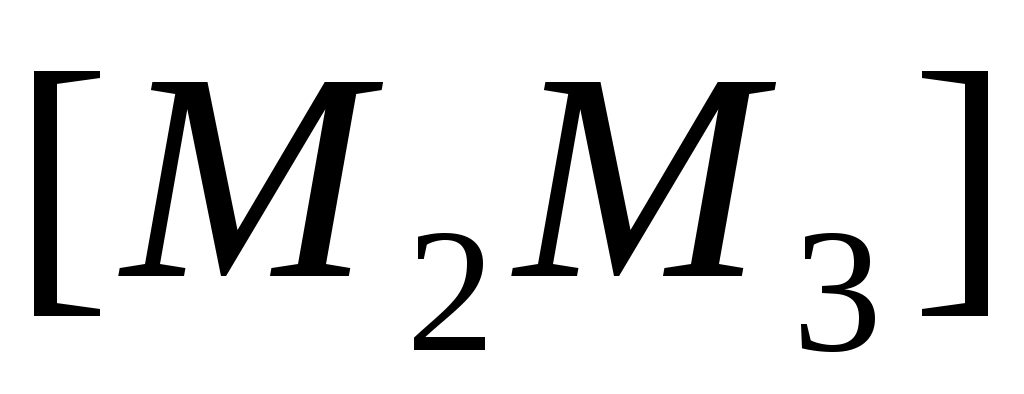 , …, , …, 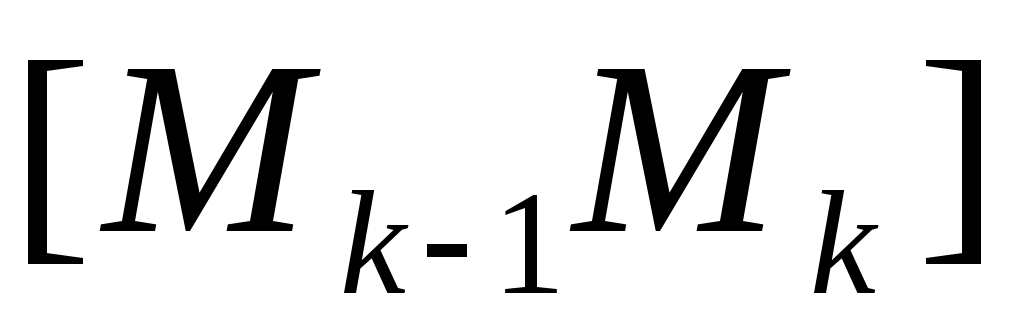 называется ломаной с вершинами называется ломаной с вершинами 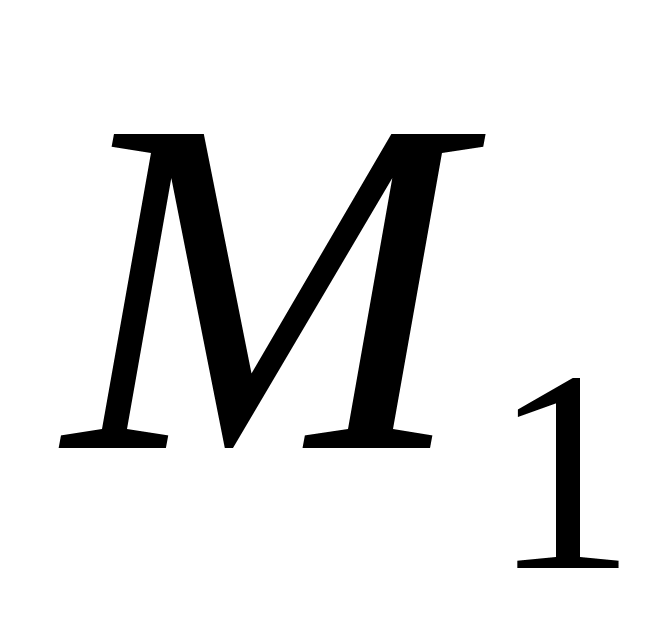 , , 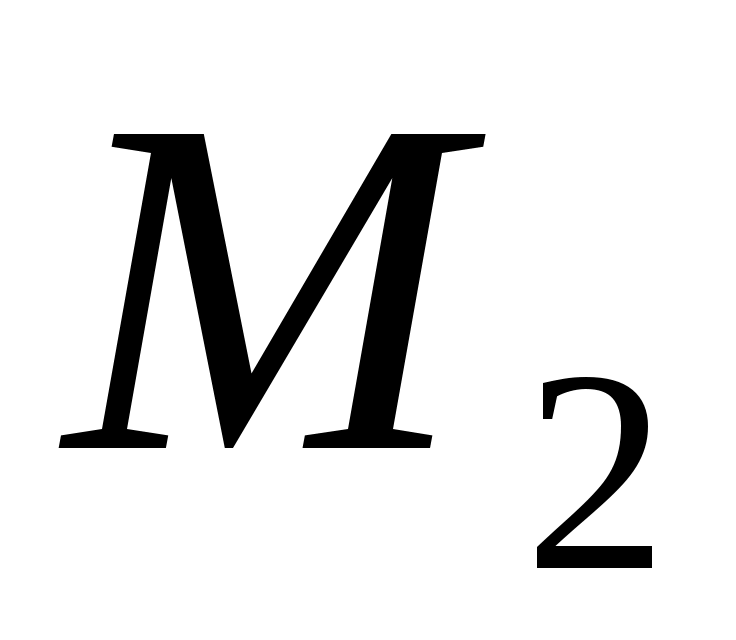 , …, , …, 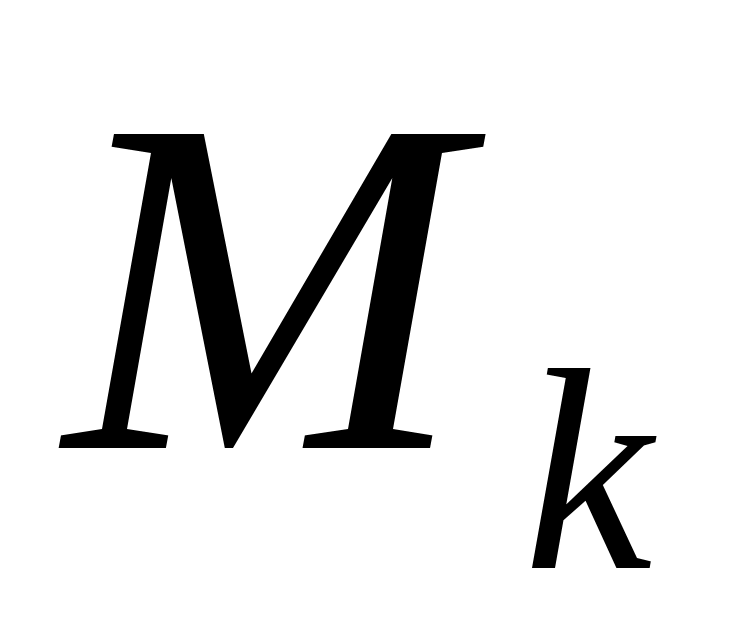 . .
ОПР. 3 Множество точек 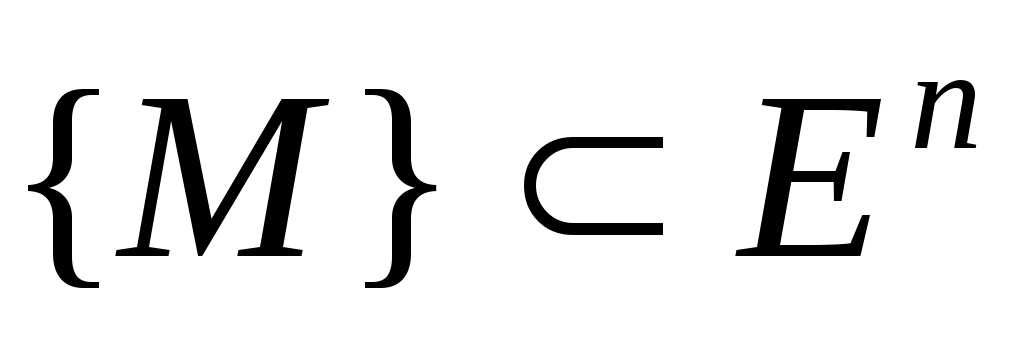 называется связным, если две любые его точки можно соединить ломаной, которая целиком содержится в данном множестве. называется связным, если две любые его точки можно соединить ломаной, которая целиком содержится в данном множестве.
ОПР. 4 Пусть дана точка 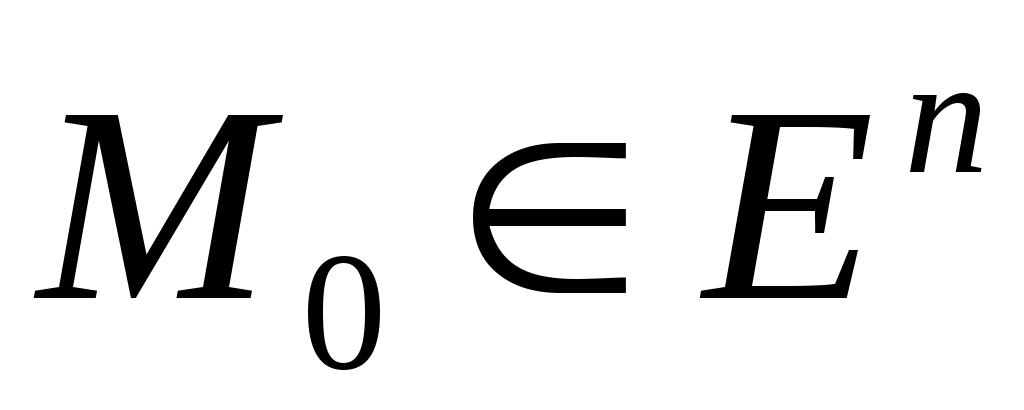 и положительное число и положительное число 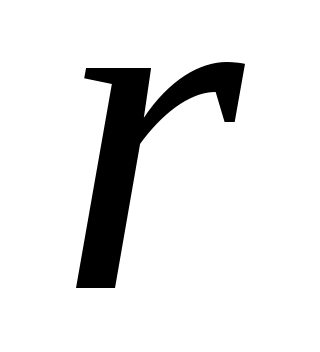 . Множество всех точек . Множество всех точек 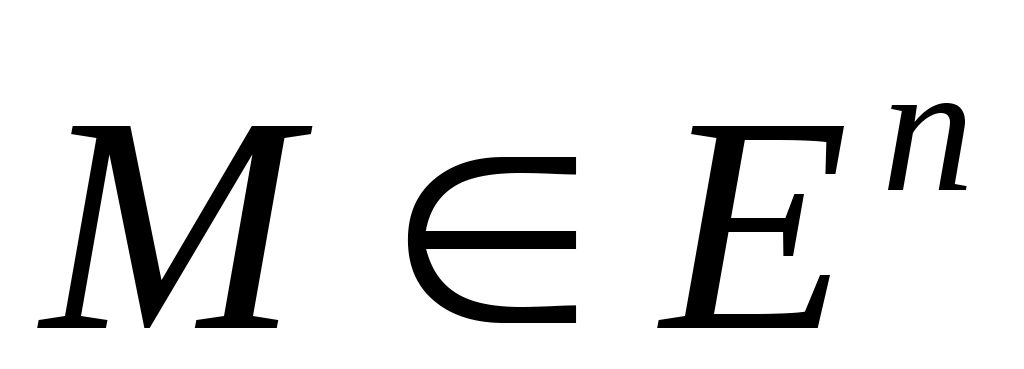 , удовлетворяющих условию , удовлетворяющих условию
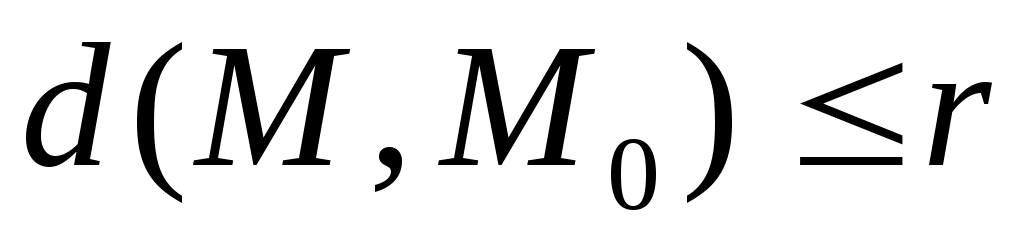 , 3 , 3
называется n – мерным шаром с центром в точке 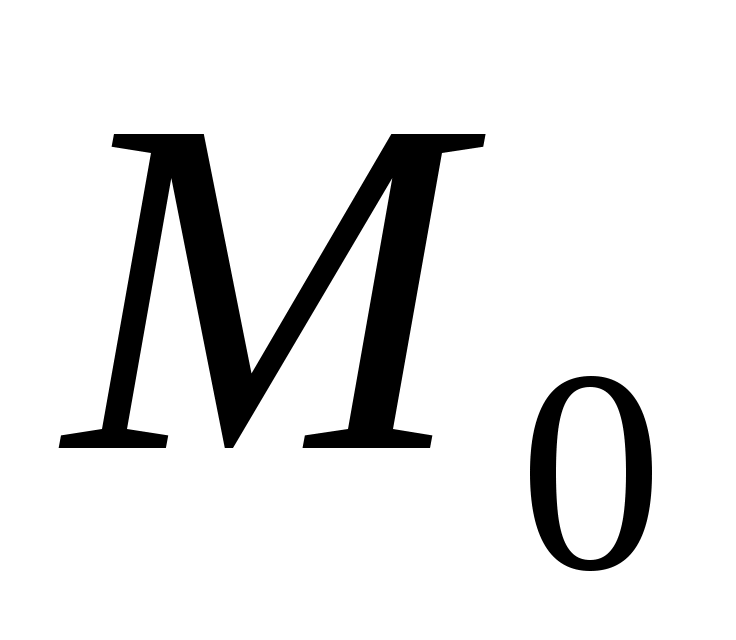 и радиусом и радиусом 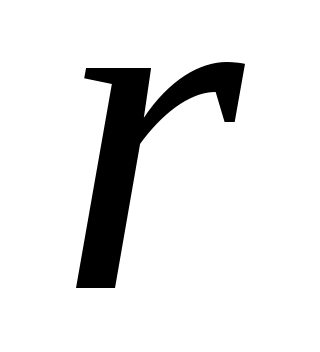 ; n – мерная сфера определяется условием ; n – мерная сфера определяется условием
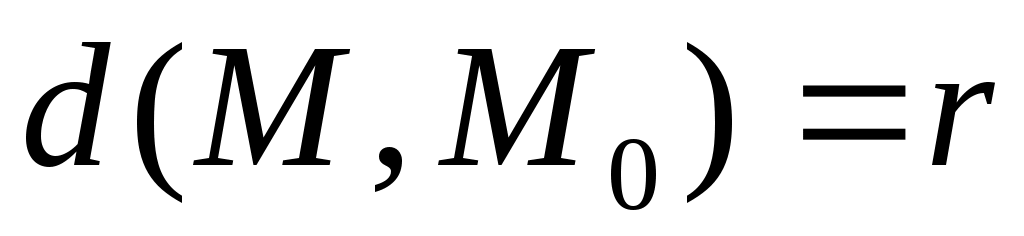 . 4 . 4
ОПР. 5 Множество точек 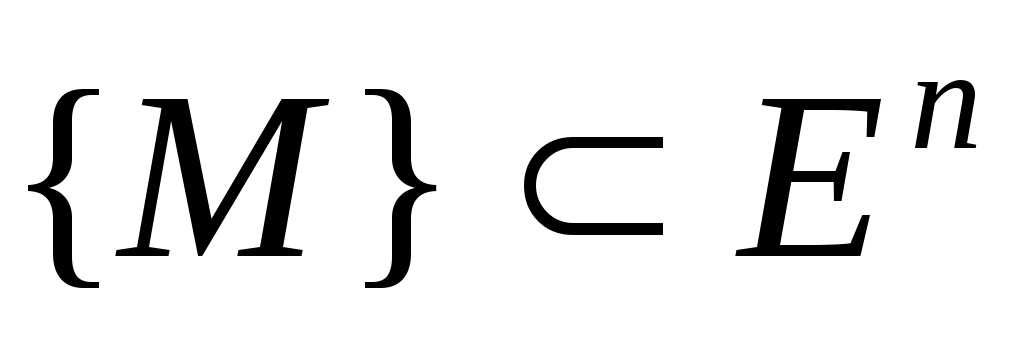 называется ограниченным, если существует такой n– мерный шар, который содержит в себе это множество. называется ограниченным, если существует такой n– мерный шар, который содержит в себе это множество.
Пример. Описать множества, представляющие собой шар и сферу в евклидовых пространствах 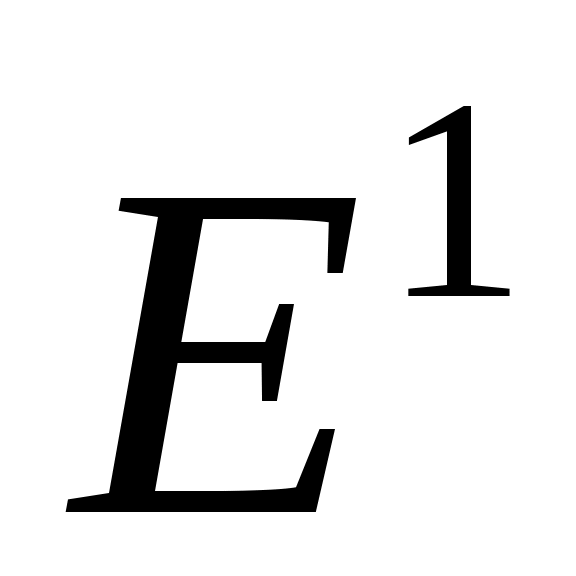 , , 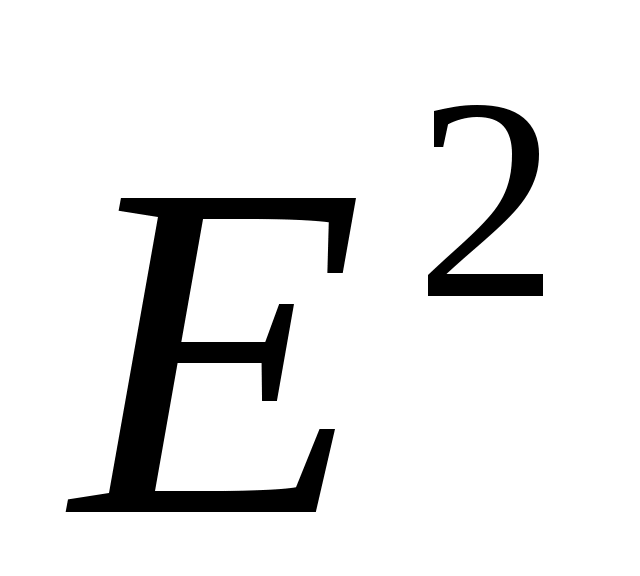 . .
1) Шаром в пространстве 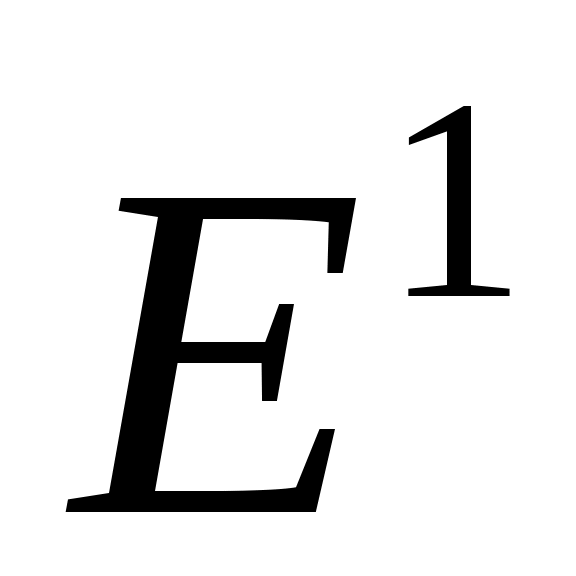 с центром в точке с центром в точке 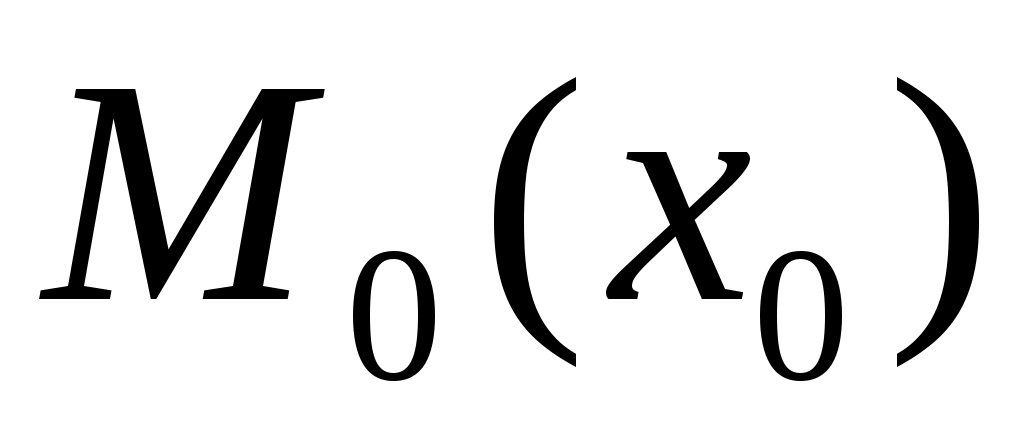 (одномерным шаром) является отрезок (одномерным шаром) является отрезок 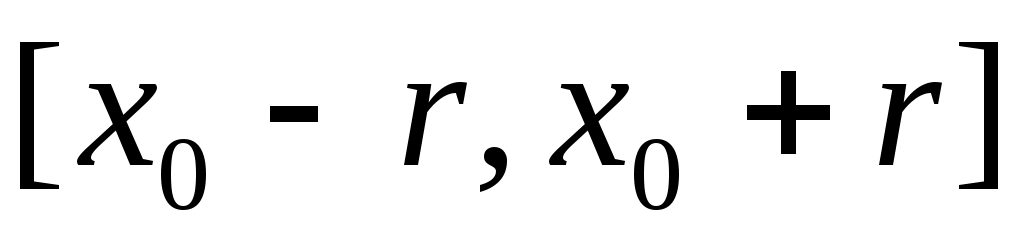 , а сферой (одномерной сферой) – пара точек, расположенных на координатной прямой симметрично относительно , а сферой (одномерной сферой) – пара точек, расположенных на координатной прямой симметрично относительно 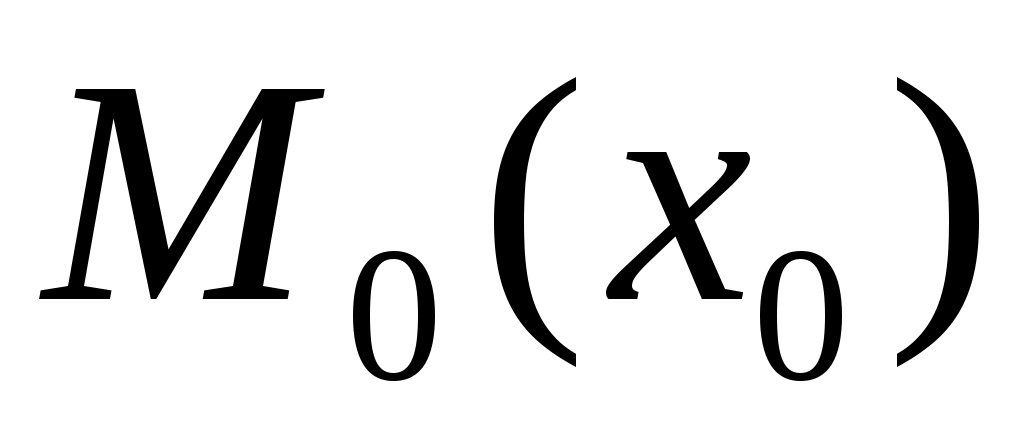 на расстоянии на расстоянии 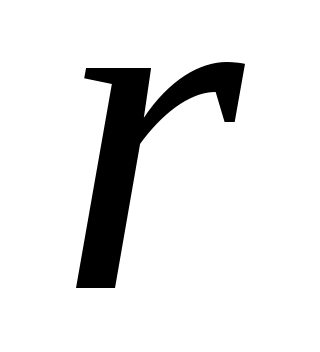 : : 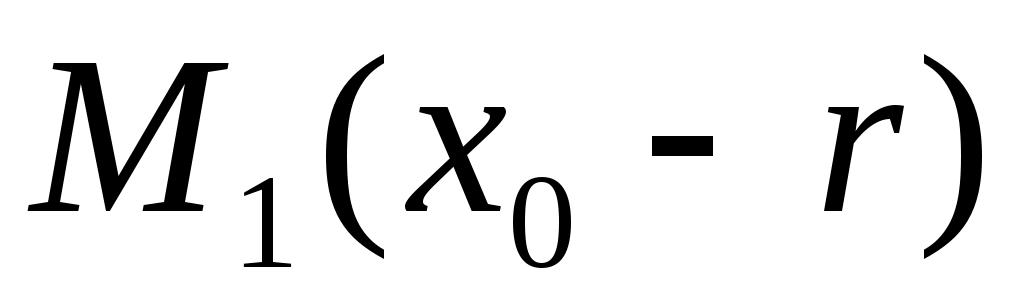 , , 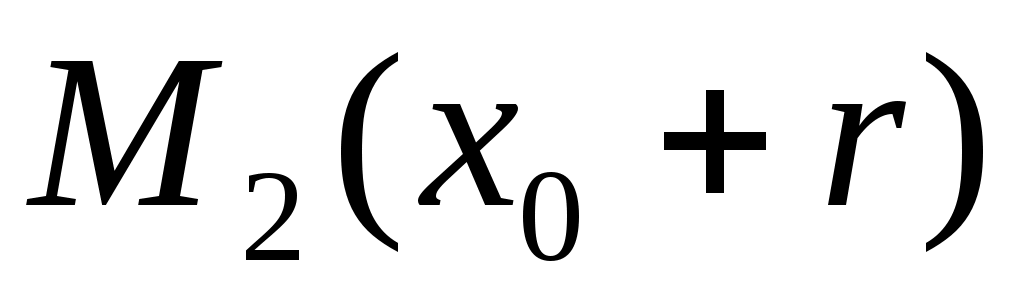 . .
2) Шаром и сферой в пространстве 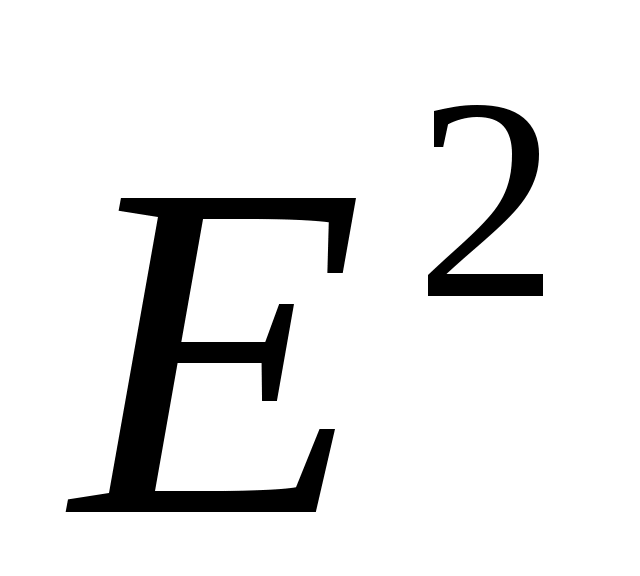 с центром в точке с центром в точке 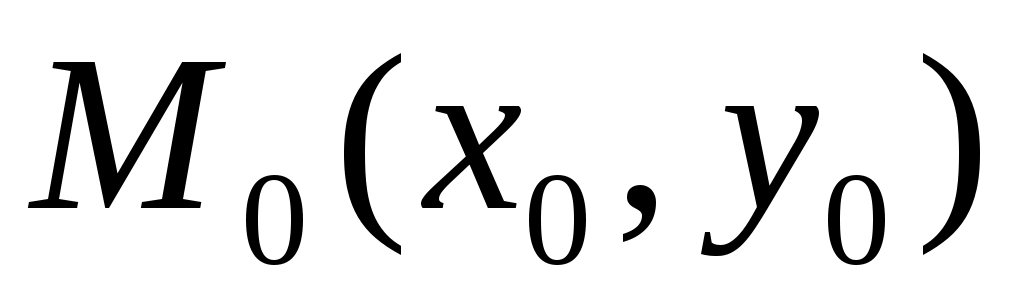 (двумерными шаром и сферой) будут соответственно круг и окружность с центром (двумерными шаром и сферой) будут соответственно круг и окружность с центром 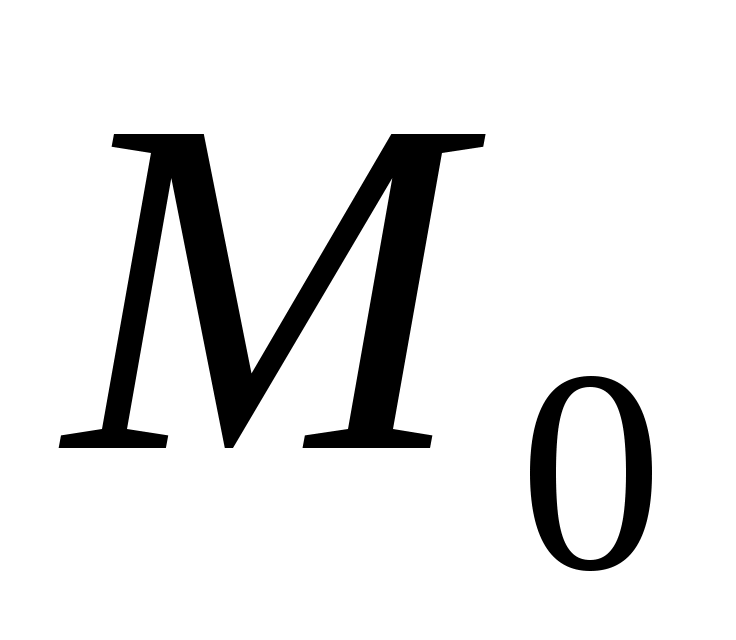 и радиусом и радиусом 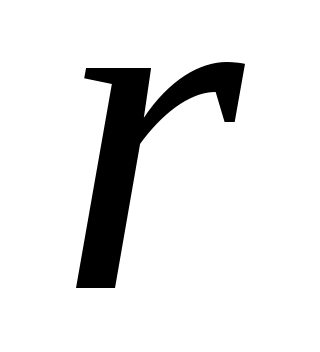 , расположенные в координатной плоскости , расположенные в координатной плоскости 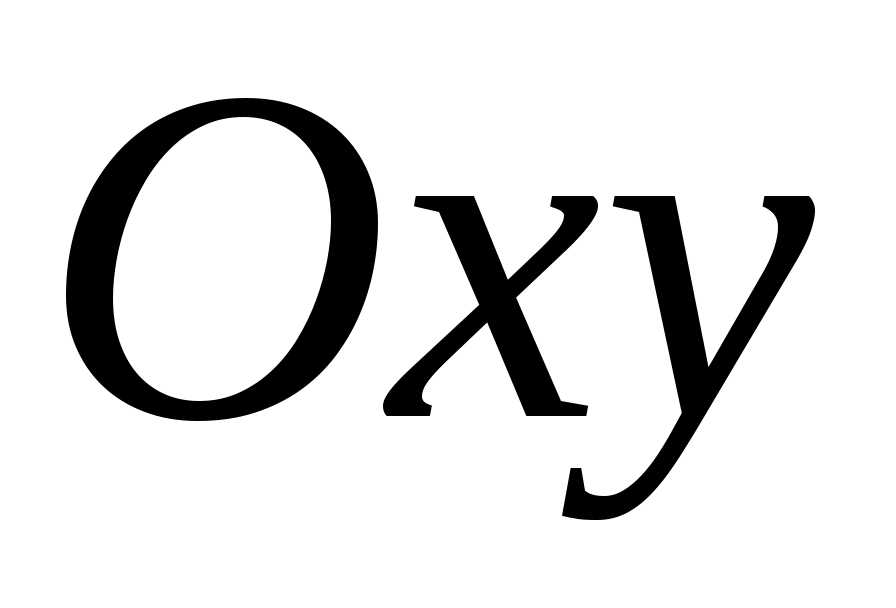 . .
ОПР. 6 Пусть дана точка 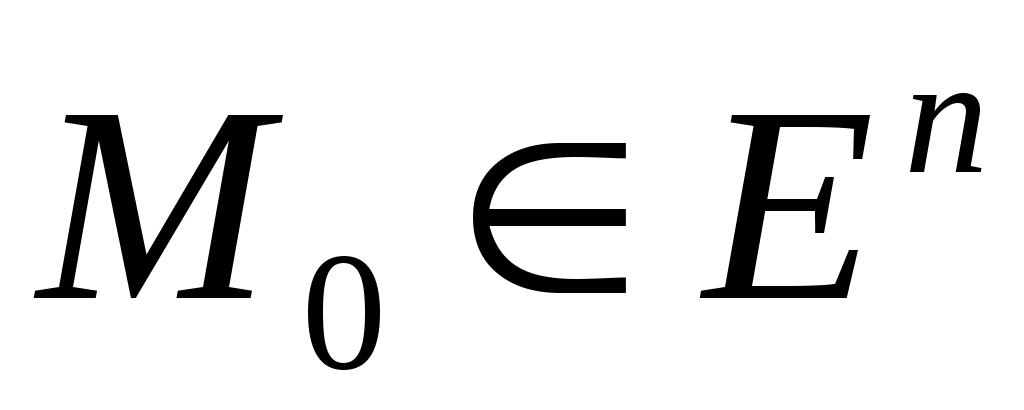 и положительное число и положительное число 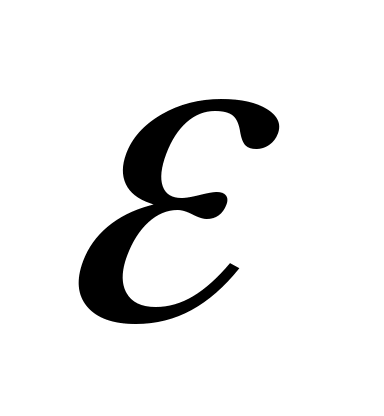 . Множество всех точек . Множество всех точек 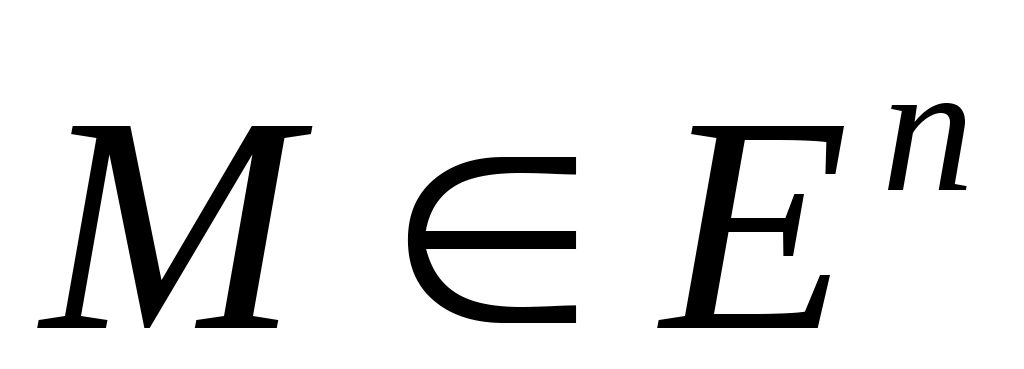 , удовлетворяющих условию , удовлетворяющих условию
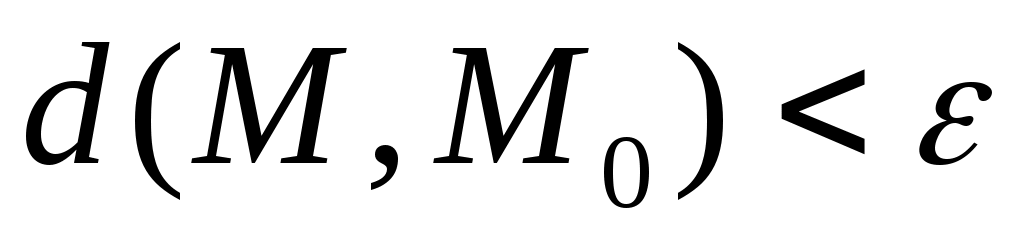 , 5 , 5
называется 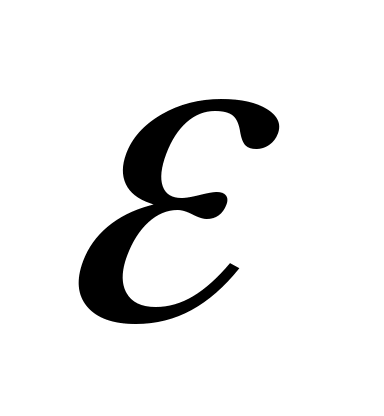 – окрестностью точки – окрестностью точки 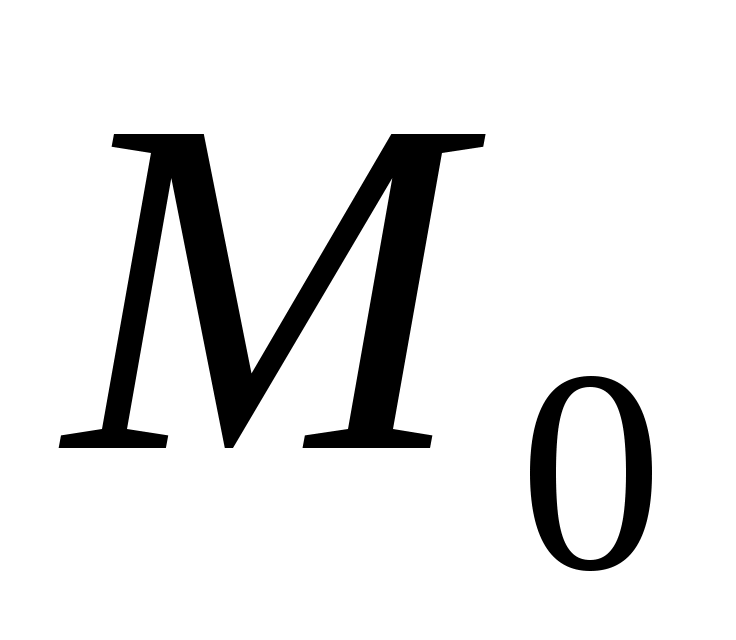 . .
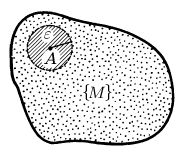
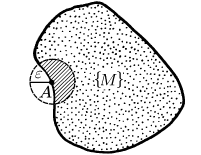
ОПР. 7 Точка 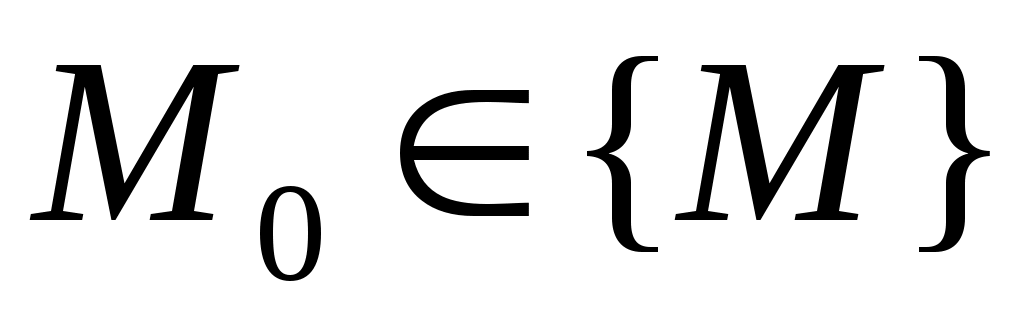 называется внутренней точкой множества называется внутренней точкой множества 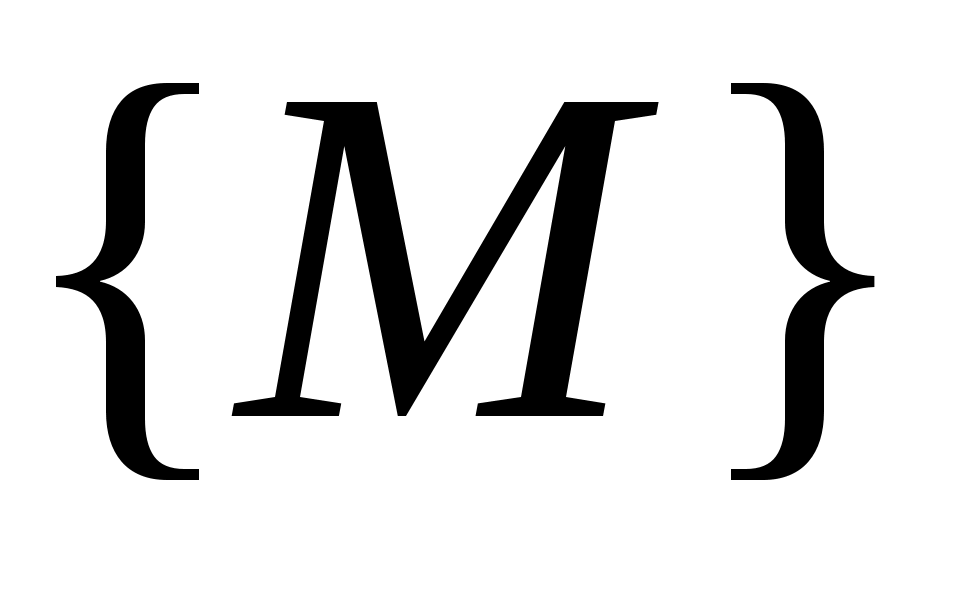 , если существует , если существует 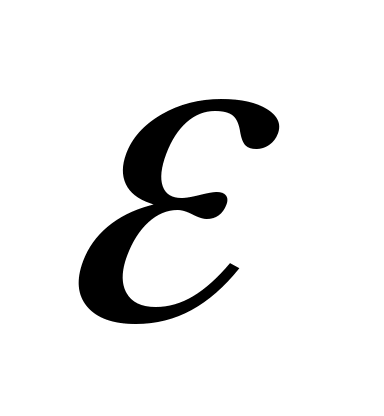 – окрестность точки – окрестность точки 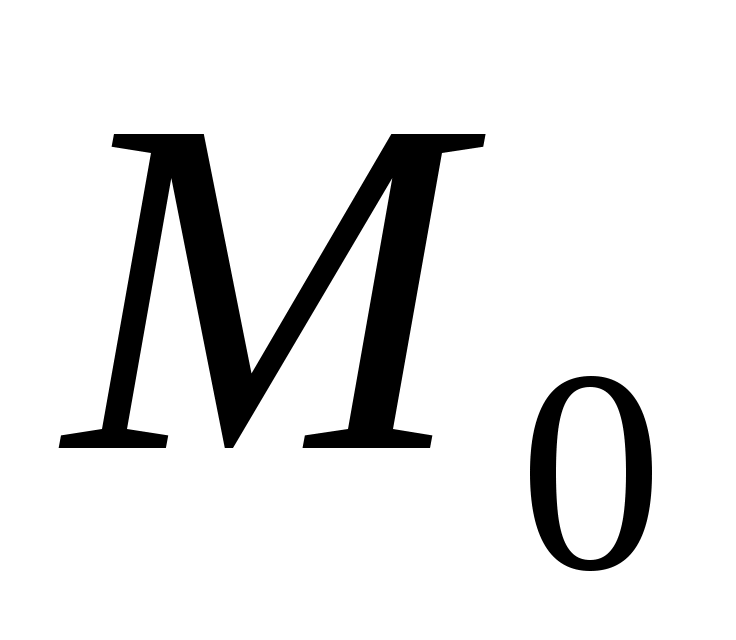 , целиком содержащаяся в данном множестве , целиком содержащаяся в данном множестве 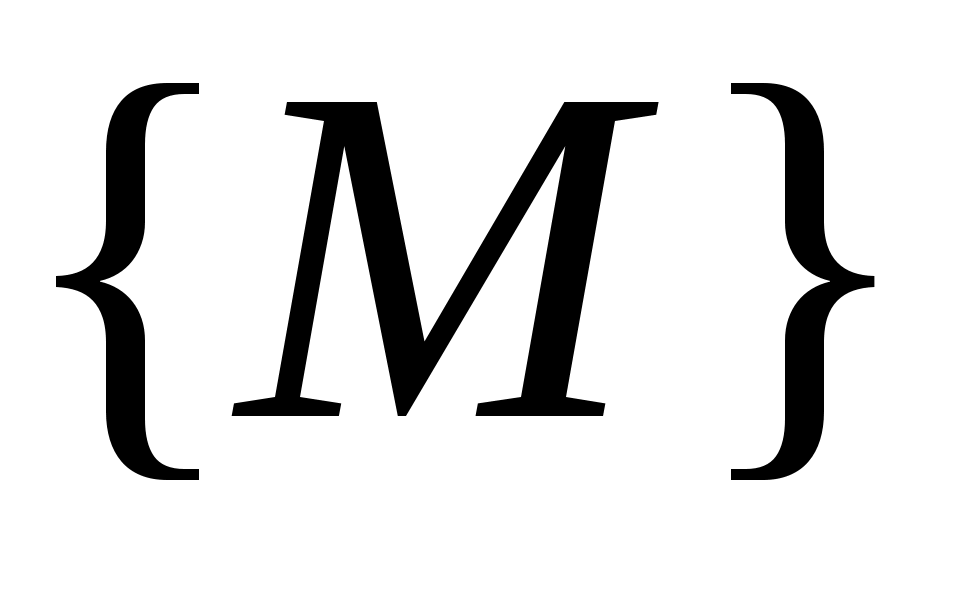 (рис. 1). (рис. 1).
ОПР. 8 Множество называется открытым, если все его точки являются внутренними.
Пример. Указать примеры открытых множеств в евклидовых пространствах 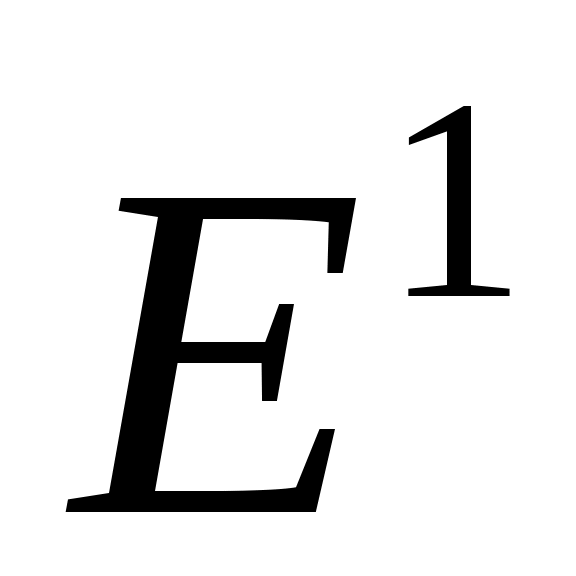 , , 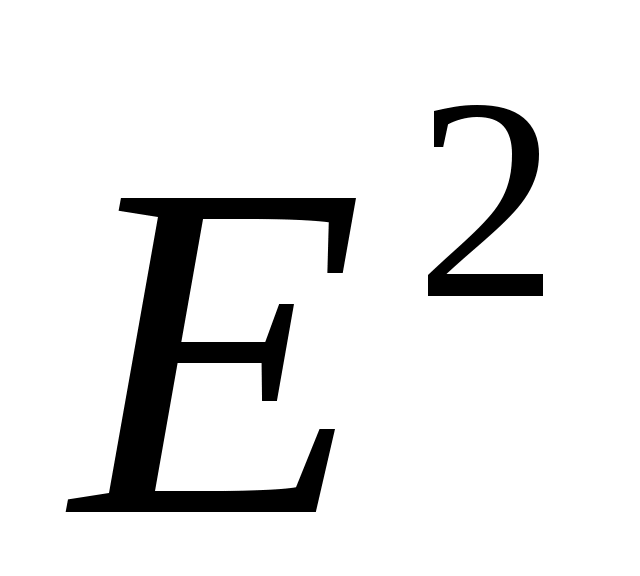 , , 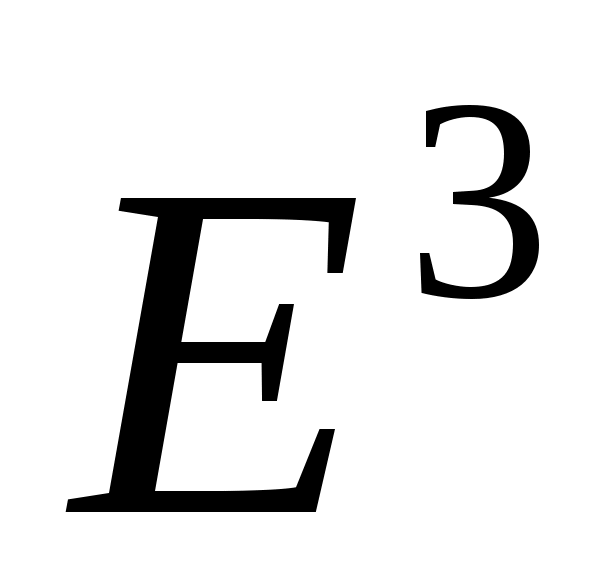 . .
РЕШЕНИЕ:
1) Открытыми множествами в пространстве 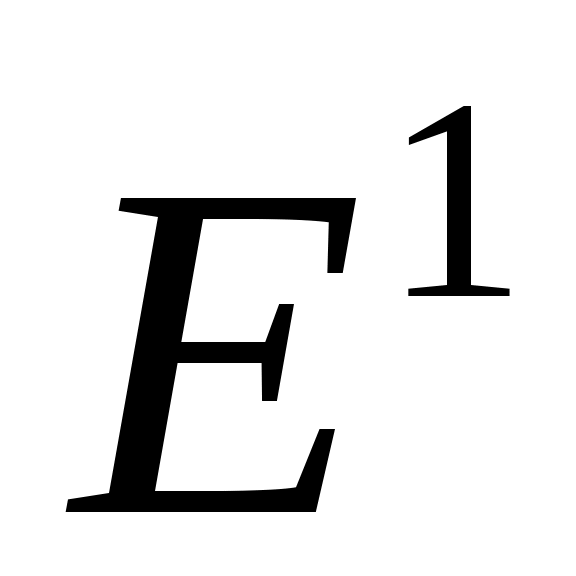 являются: интервал являются: интервал 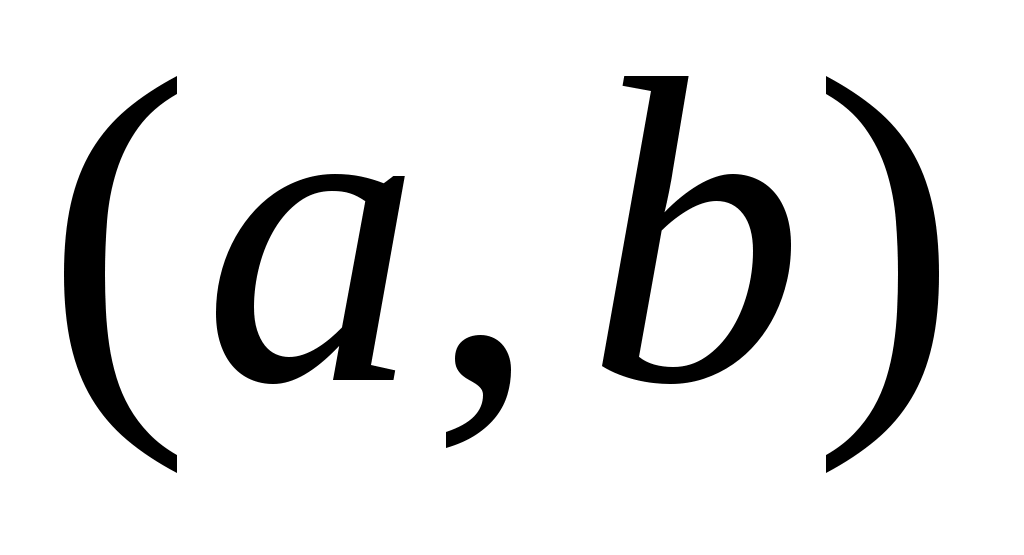 , луч , луч 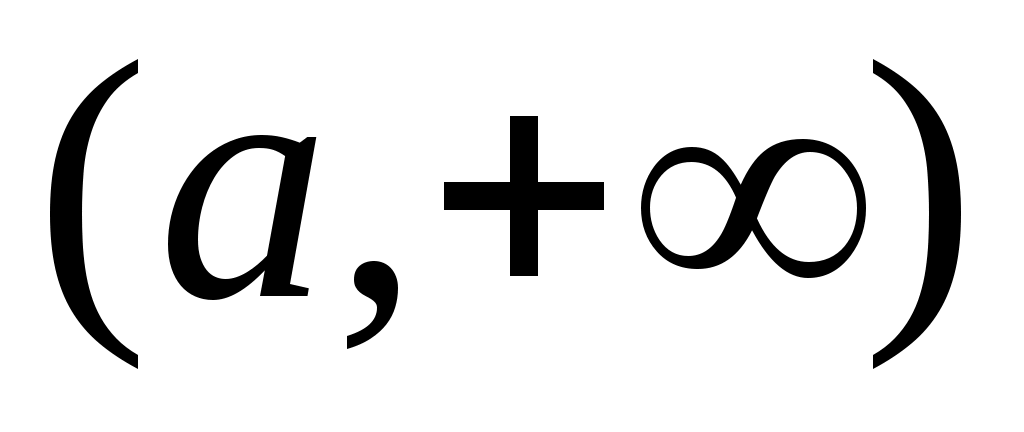 , вся числовая прямая , вся числовая прямая 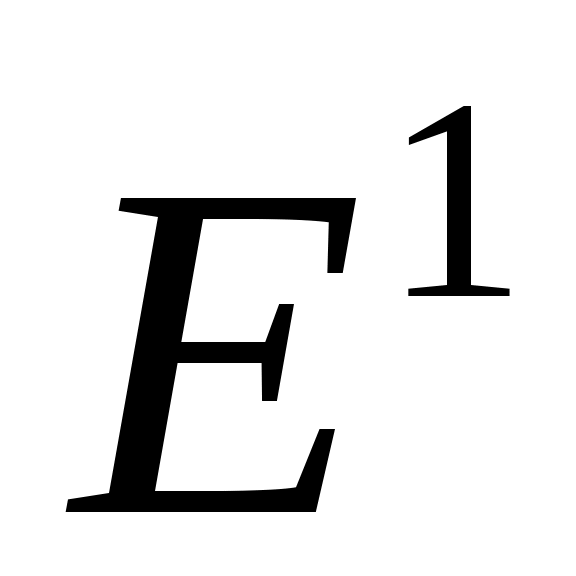 . .
2) В пространстве 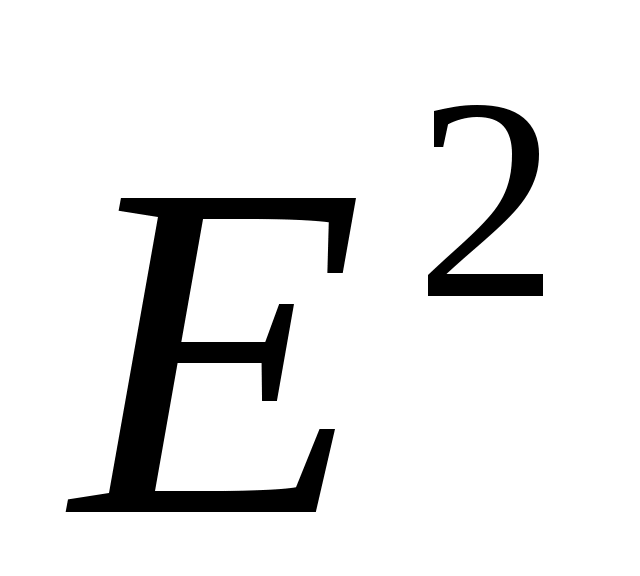 открытыми множествами будут круг без граничной окружности (открытый круг) и вся координатная плоскость открытыми множествами будут круг без граничной окружности (открытый круг) и вся координатная плоскость 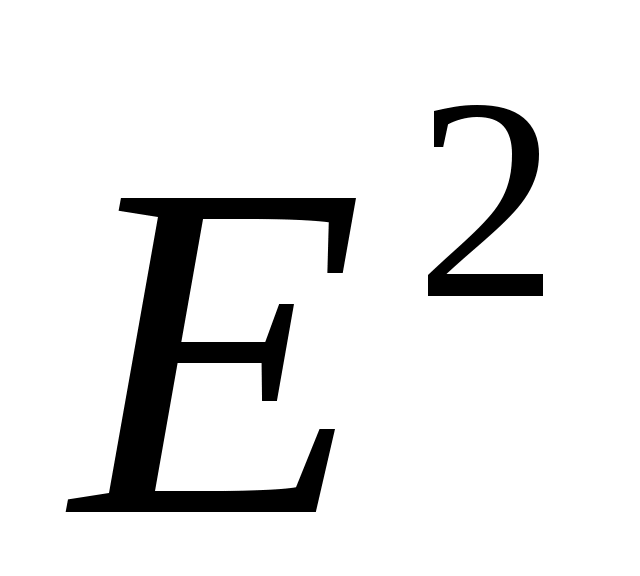 . .
3) В пространстве 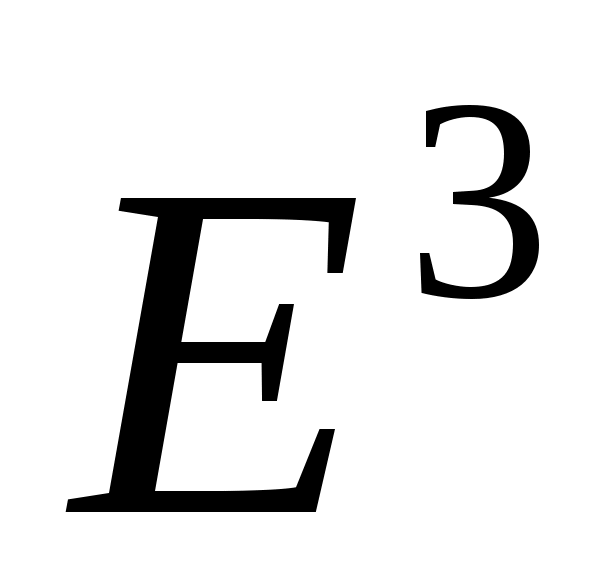 – шар без сферы (открытый шар) и все трехмерное пространство – шар без сферы (открытый шар) и все трехмерное пространство 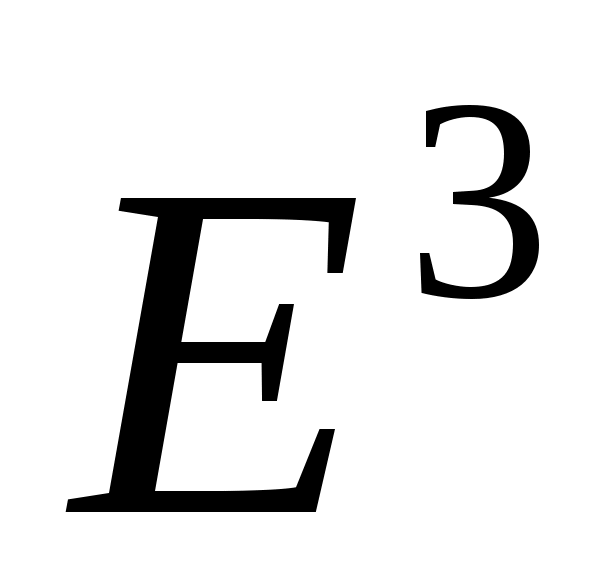 . .
ОПР. 7 Точка 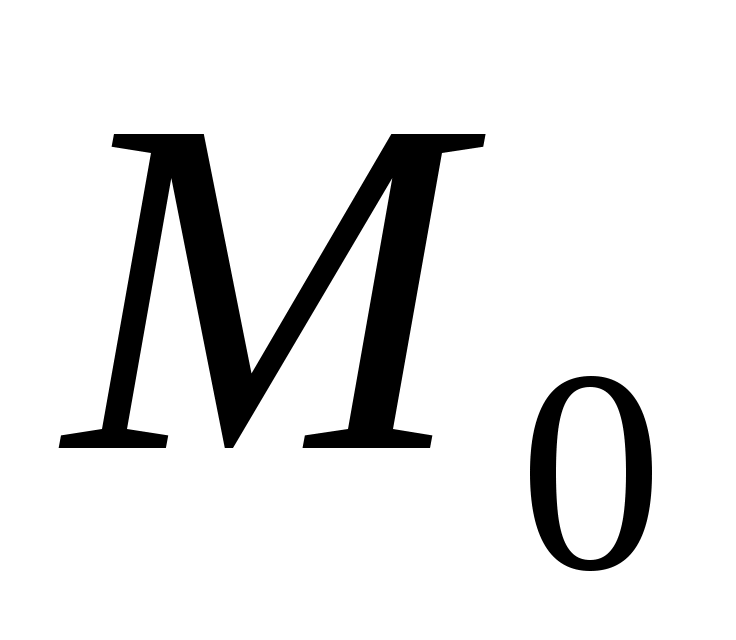 называется граничной точкой множества называется граничной точкой множества 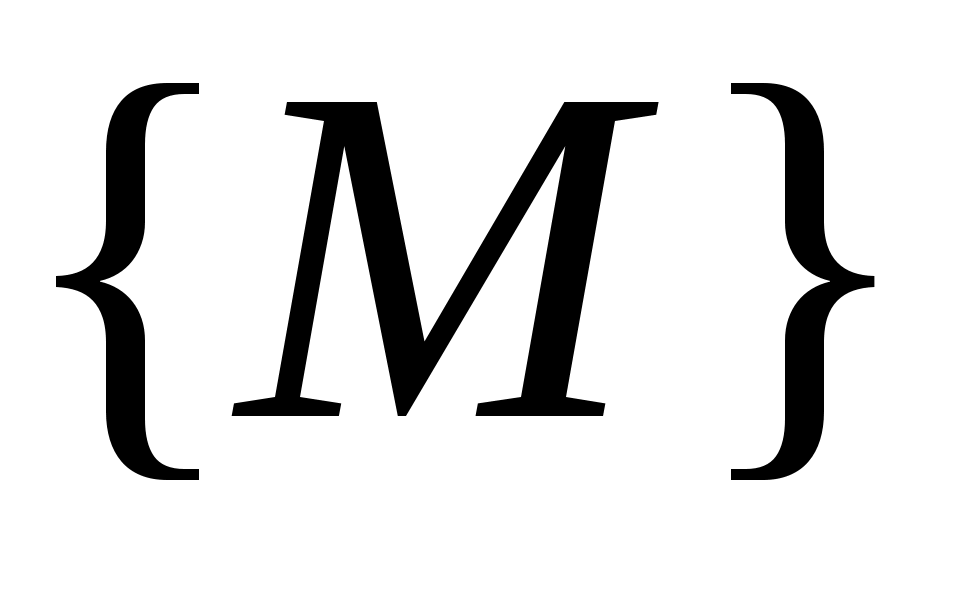 , если в любой , если в любой 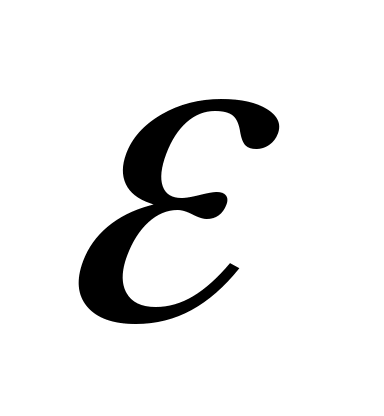 – окрестности точки – окрестности точки 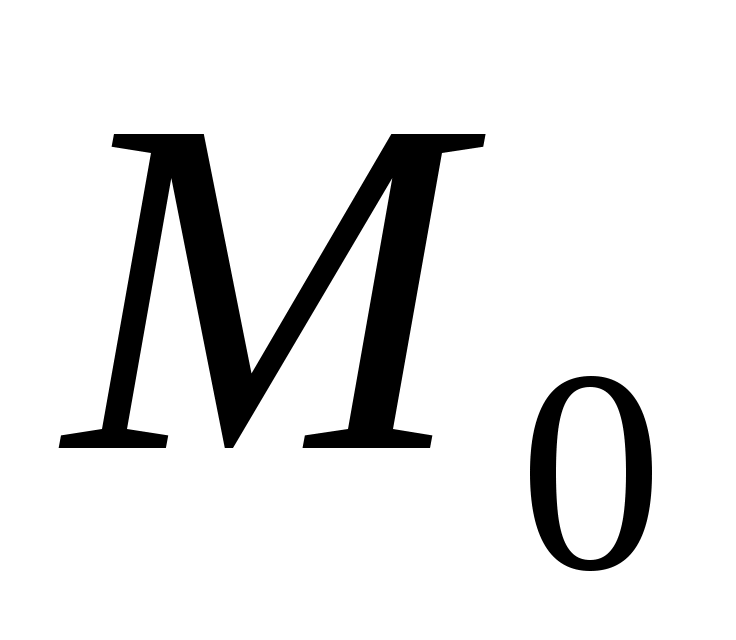 имеются как точки, принадлежащие множеству имеются как точки, принадлежащие множеству 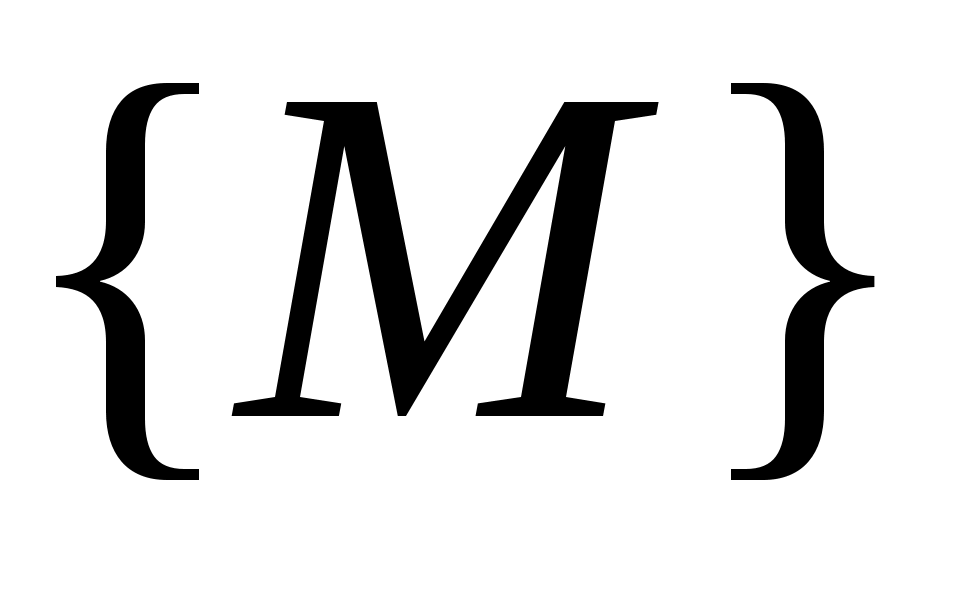 , так и точки, ему не принадлежащие (рис. 2). , так и точки, ему не принадлежащие (рис. 2).
|
|
Рис. 1
|
Рис. 2
|
Множество всех граничных точек множества 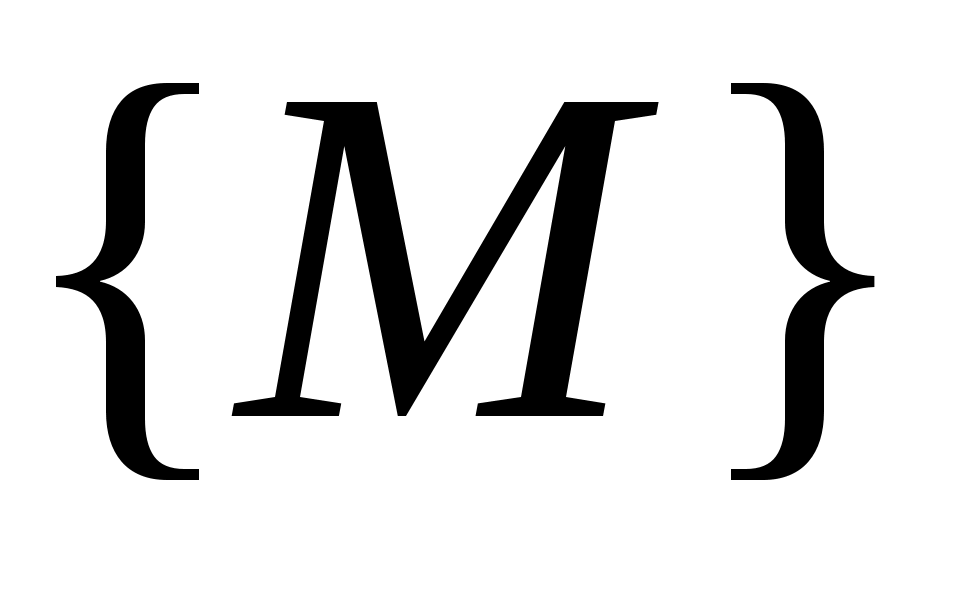 называется его границей. называется его границей.
Множество называется замкнутым, если оно содержит в себе свою границу.
Пример. Указать примеры замкнутых множеств в евклидовых пространствах 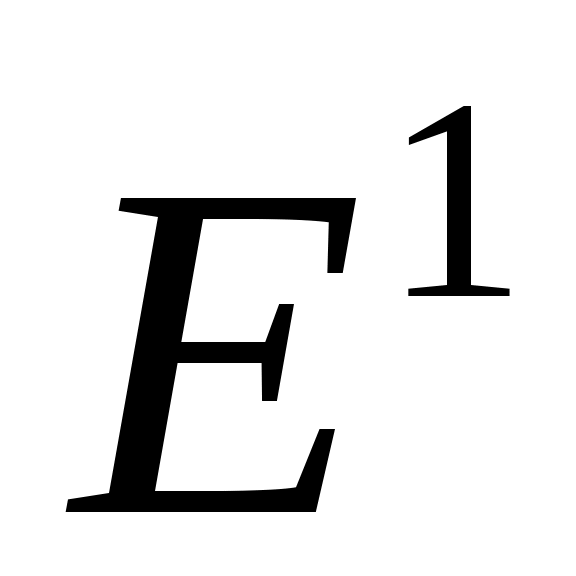 , , 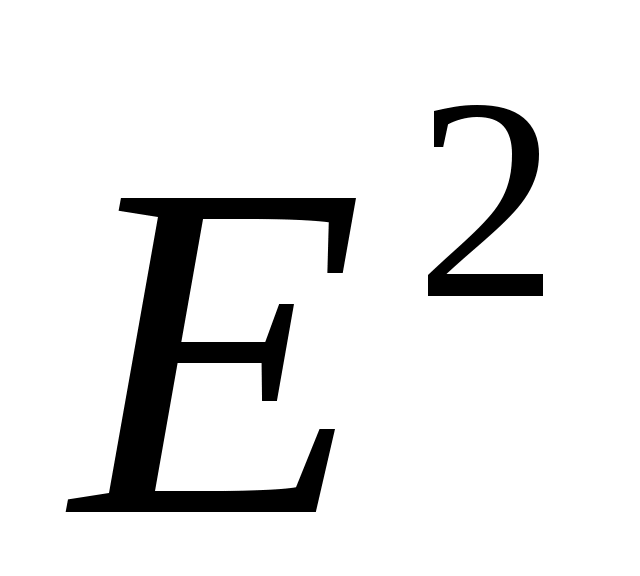 , , 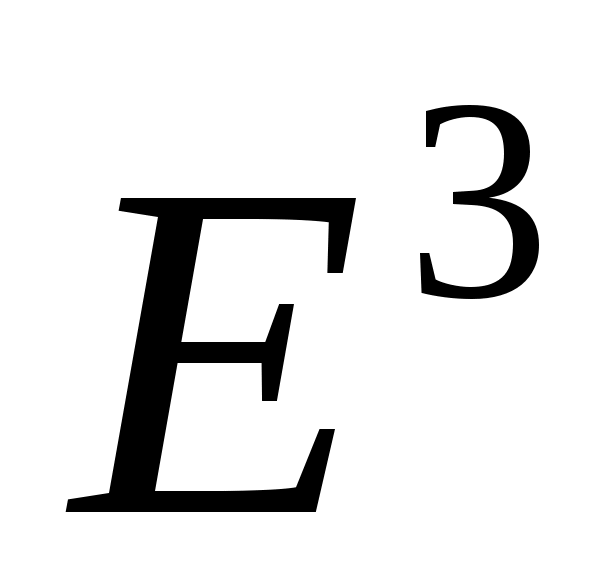 . .
РЕШЕНИЕ:
1) Замкнутыми множествами в пространстве 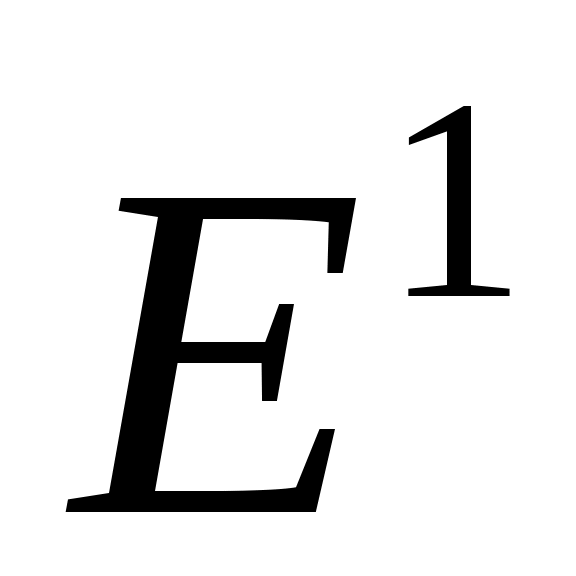 являются, например, отрезок являются, например, отрезок 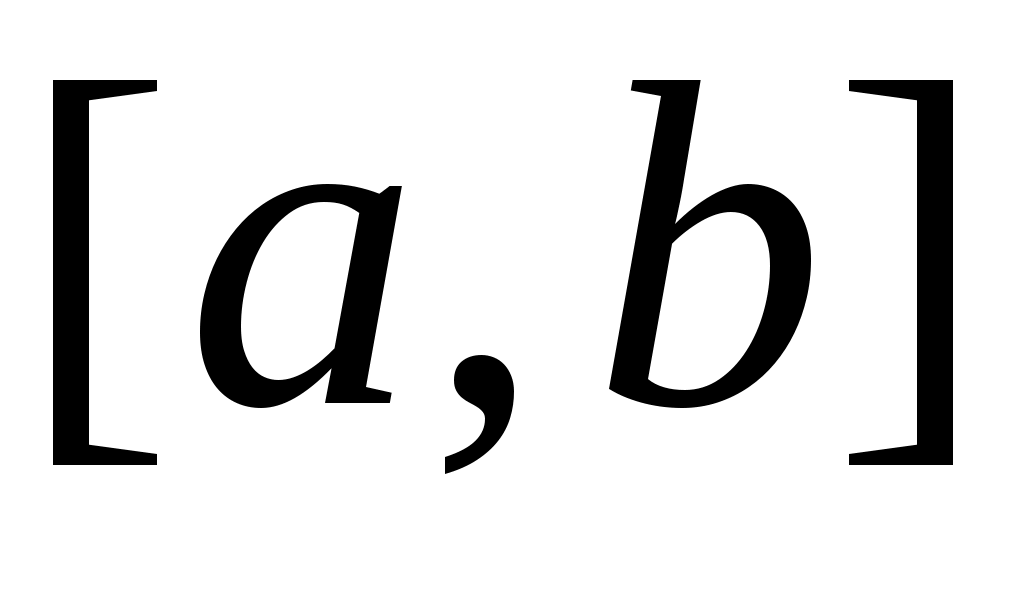 , луч , луч 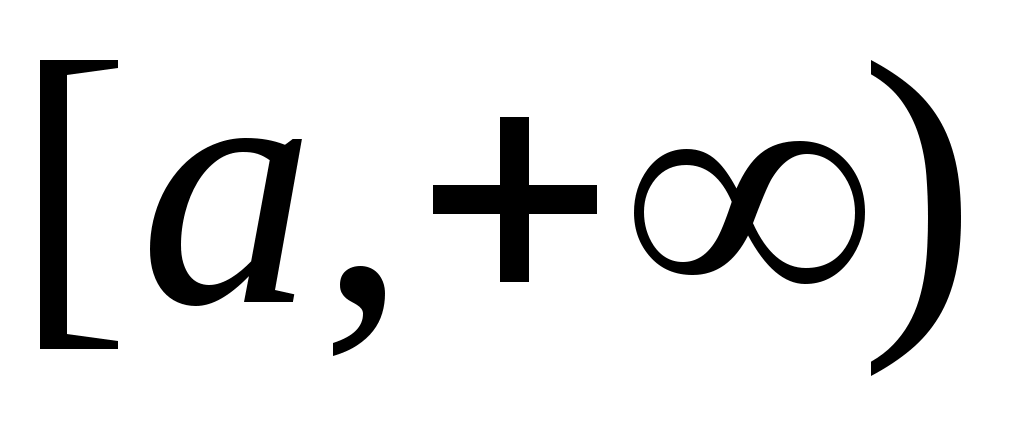 , вся числовая прямая , вся числовая прямая 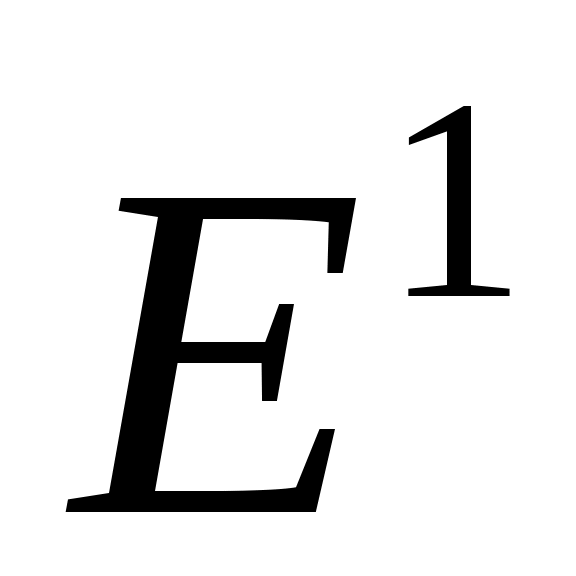 . .
2) В пространстве 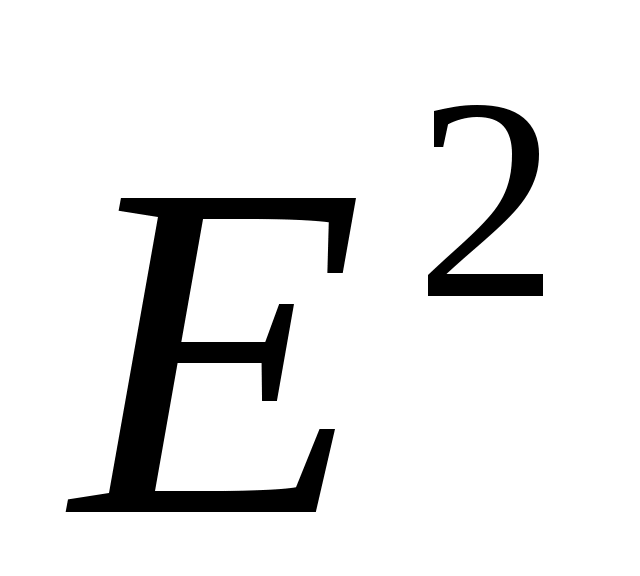 замкнутыми множествами будут круг и прямоугольник вместе со своими границами и вся координатная плоскость замкнутыми множествами будут круг и прямоугольник вместе со своими границами и вся координатная плоскость 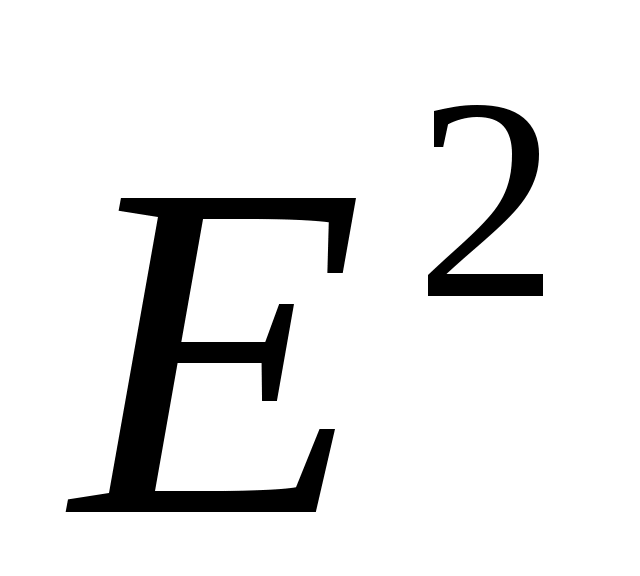 . .
3) В пространстве 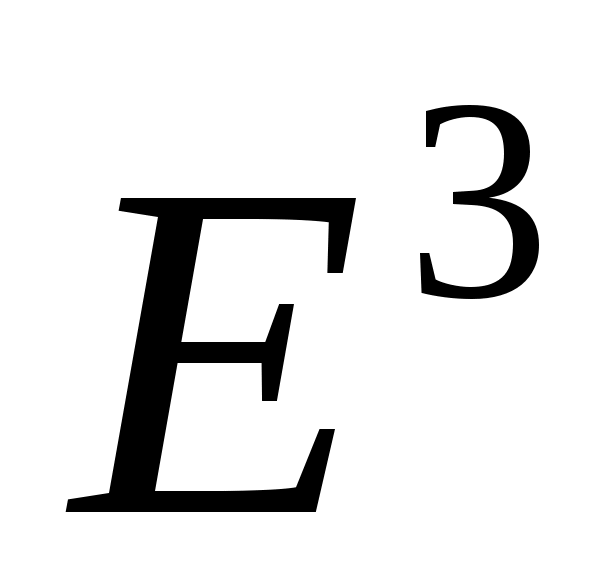 – шар, параллелепипед и все трехмерное пространство – шар, параллелепипед и все трехмерное пространство 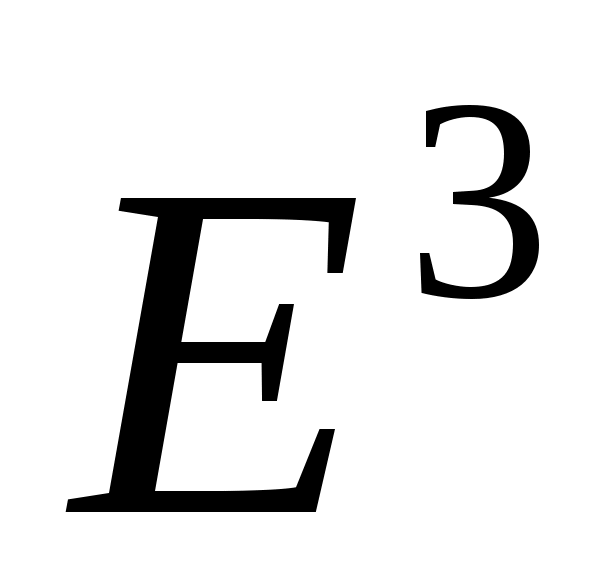 . .
ОПР. 9 Точка 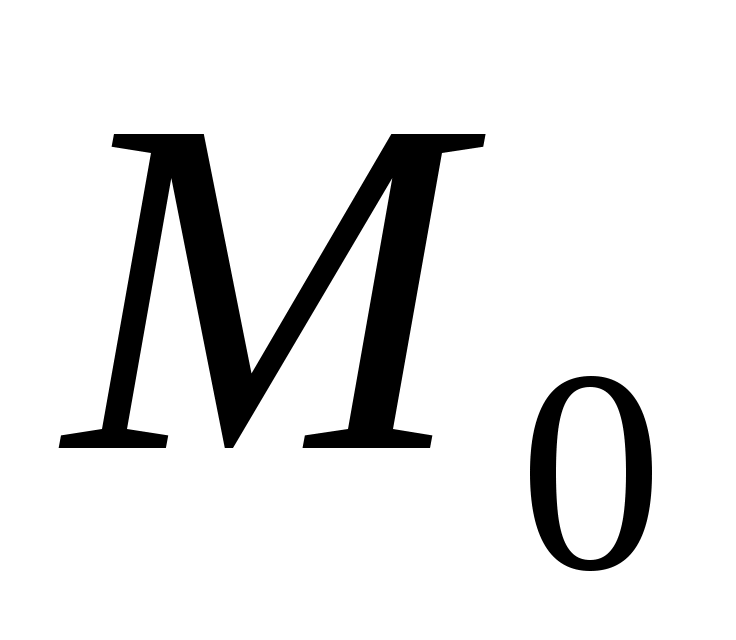 называется предельной точкой множества называется предельной точкой множества 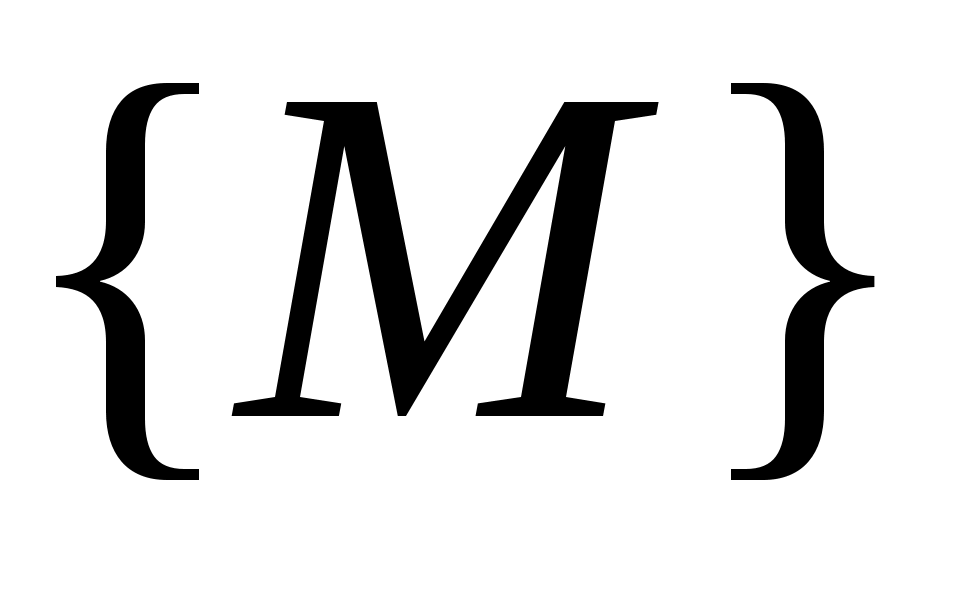 , если в любой , если в любой 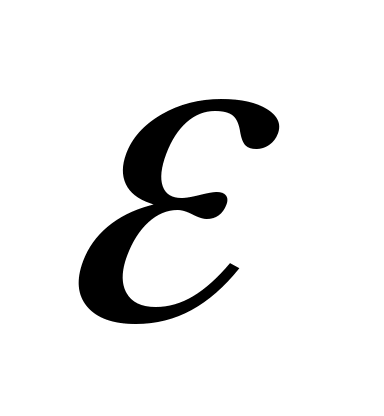 – окрестности точки – окрестности точки 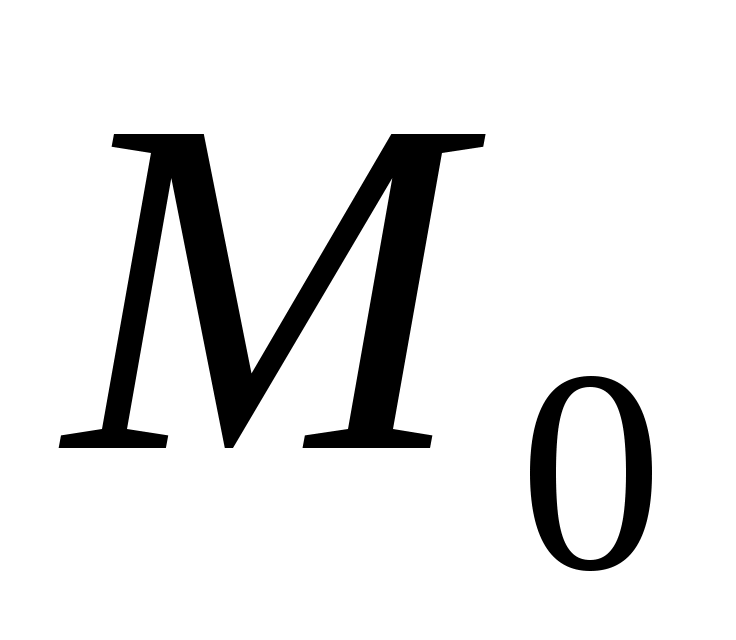 содержится хотя бы одна точка множества содержится хотя бы одна точка множества 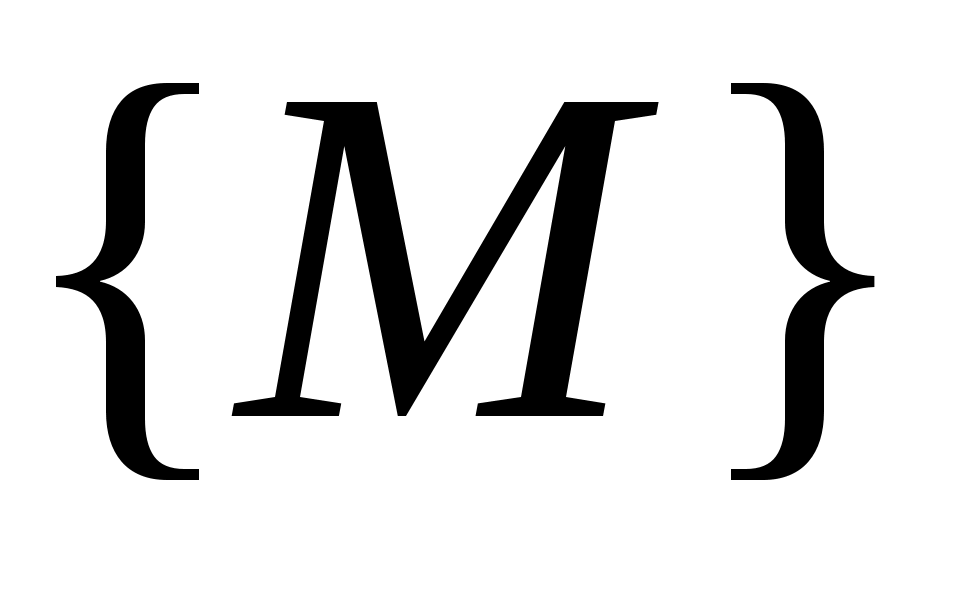 , отличная от , отличная от 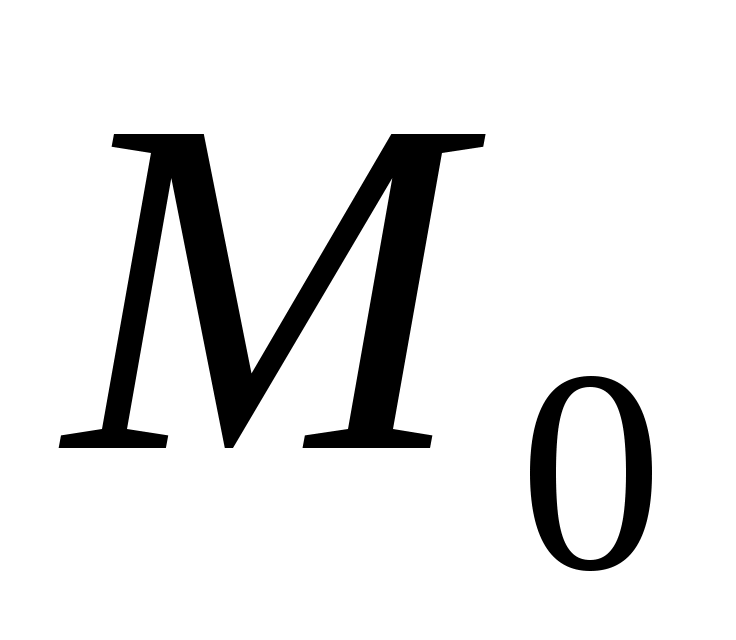 . По-другому: точка . По-другому: точка 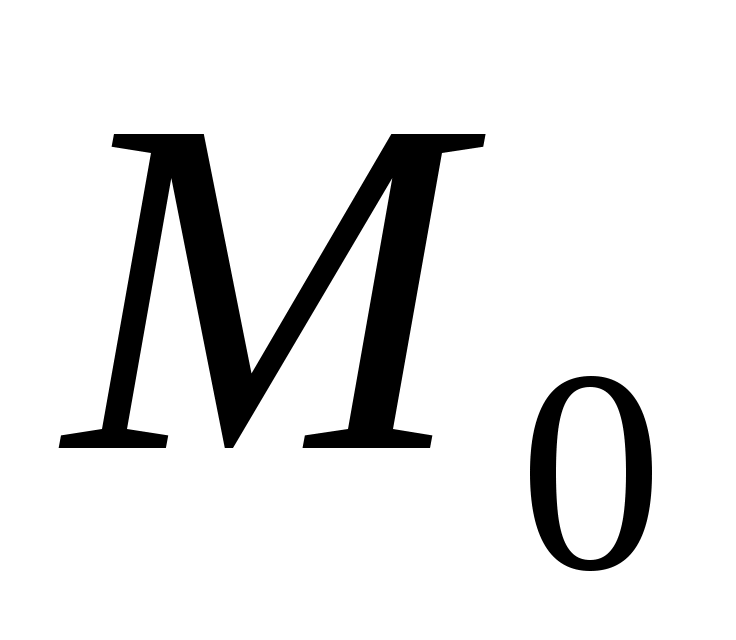 является предельной для является предельной для 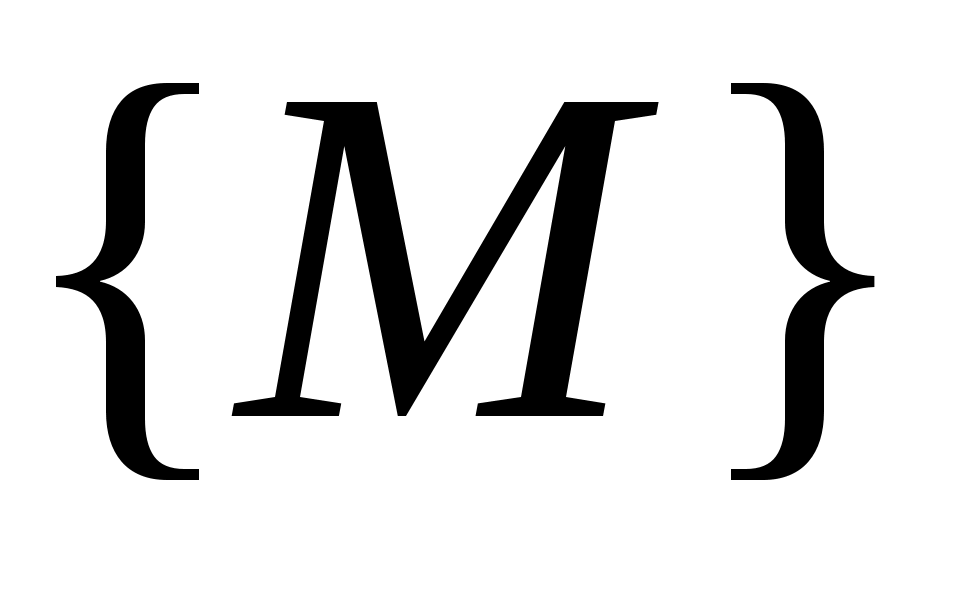 , если к этой точке можно «подойти сколь угодно близко, идя по точкам множества , если к этой точке можно «подойти сколь угодно близко, идя по точкам множества 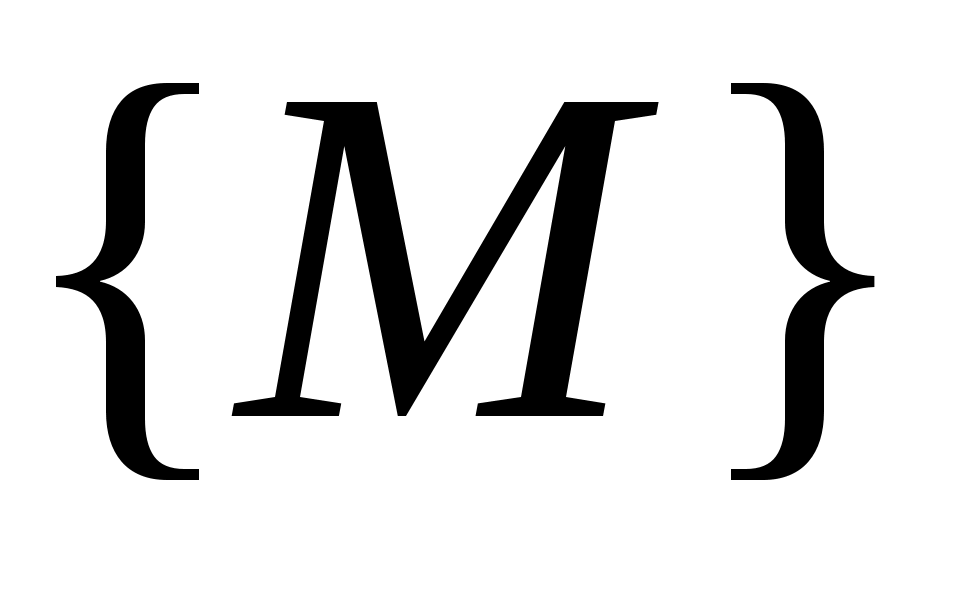 и не наступая на саму точку и не наступая на саму точку 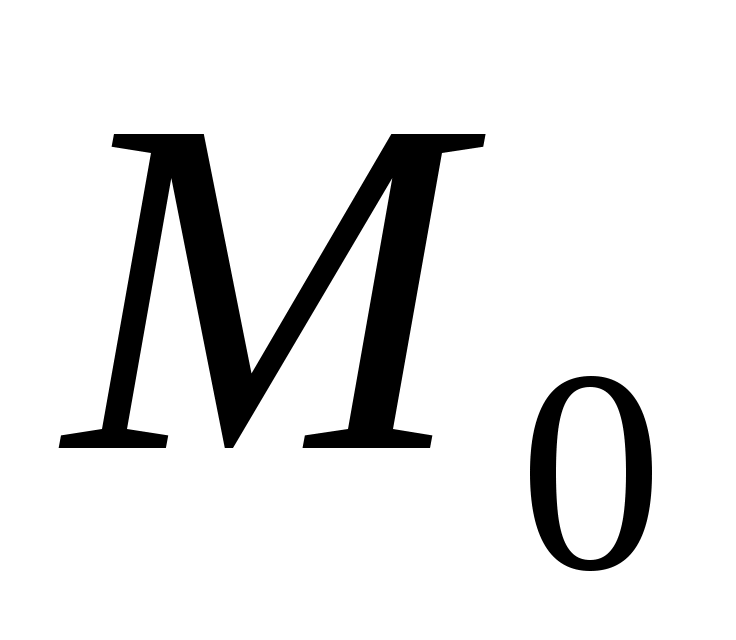 », которая сама может принадлежать, а может не принадлежать этому множеству. », которая сама может принадлежать, а может не принадлежать этому множеству.
ОПР. 10 Открытое связное множество называется областью, а объединение области и ее границы – замкнутой областью.
II ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть 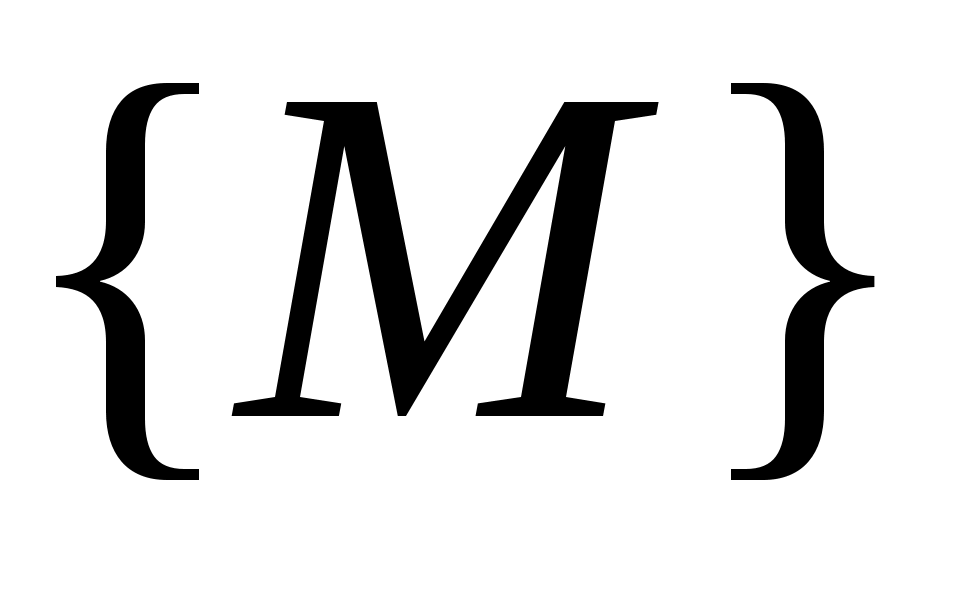 – множество точек пространства – множество точек пространства 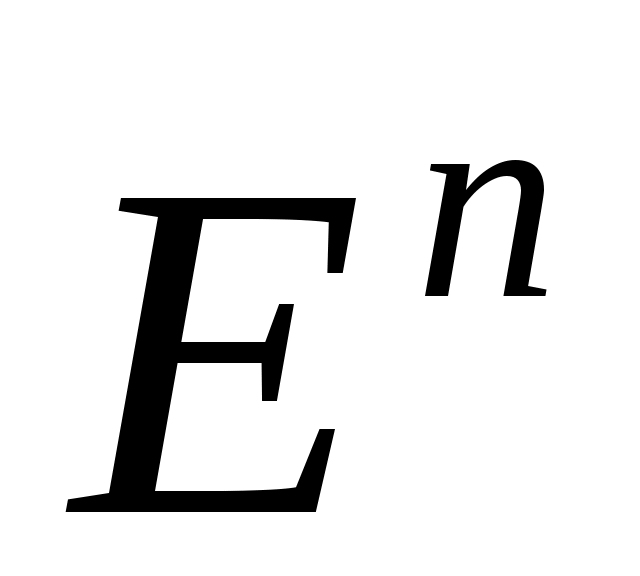 . .
ОПР. 11 Если каждой точке 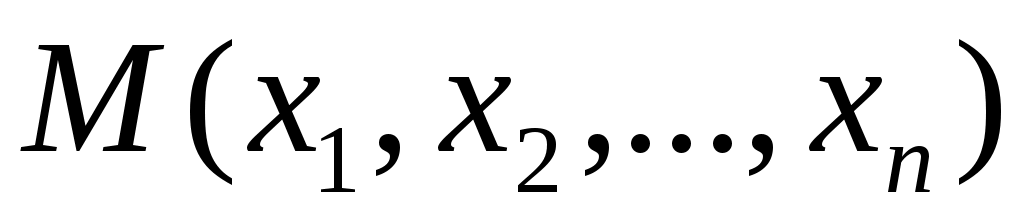 , принадлежащей множеству , принадлежащей множеству 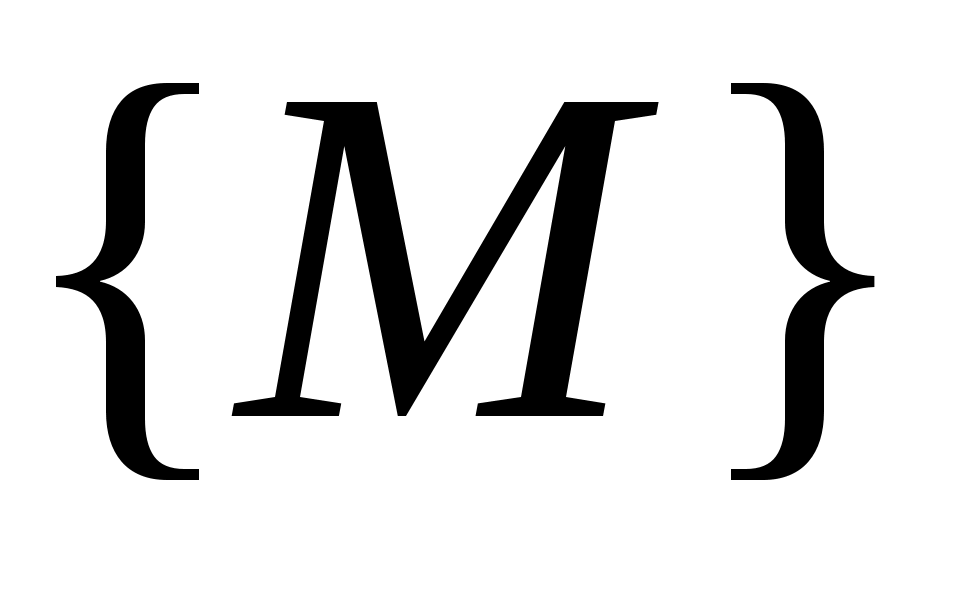 , по определенному правилу ставится в соответствие единственное число u, то говорят, что на множестве , по определенному правилу ставится в соответствие единственное число u, то говорят, что на множестве 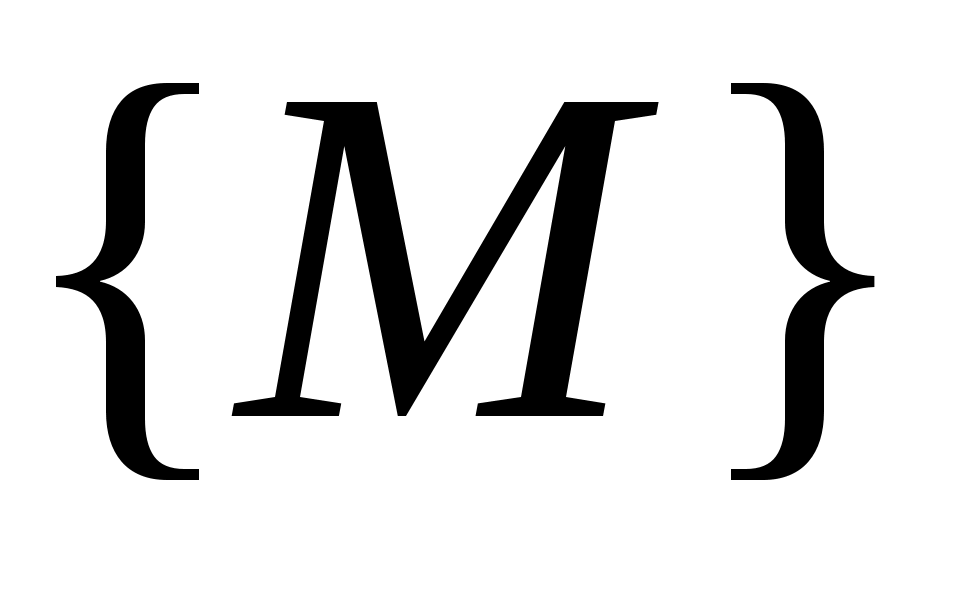 задана функция n переменных, обозначаемая задана функция n переменных, обозначаемая 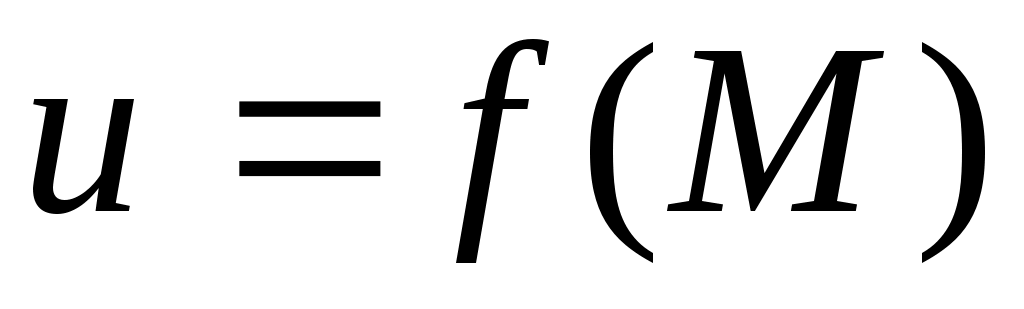 или или 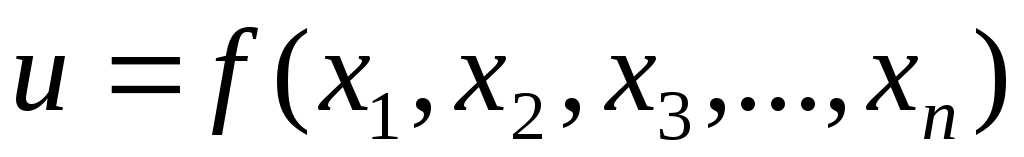 . Иногда функцию . Иногда функцию 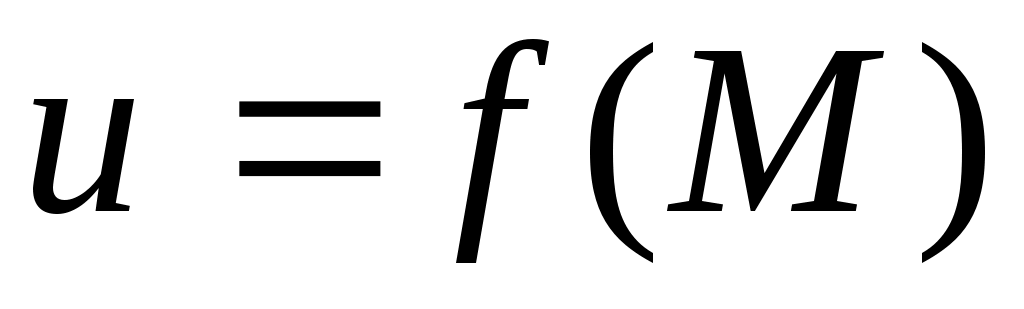 называют функцией точки, или отображением, или скалярным полем. называют функцией точки, или отображением, или скалярным полем.
Числовые переменные 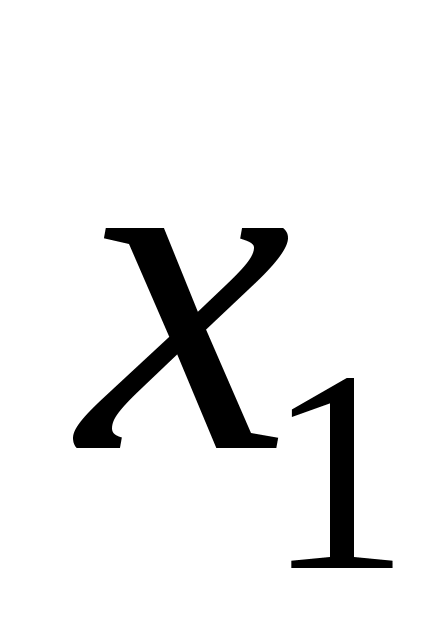 , , 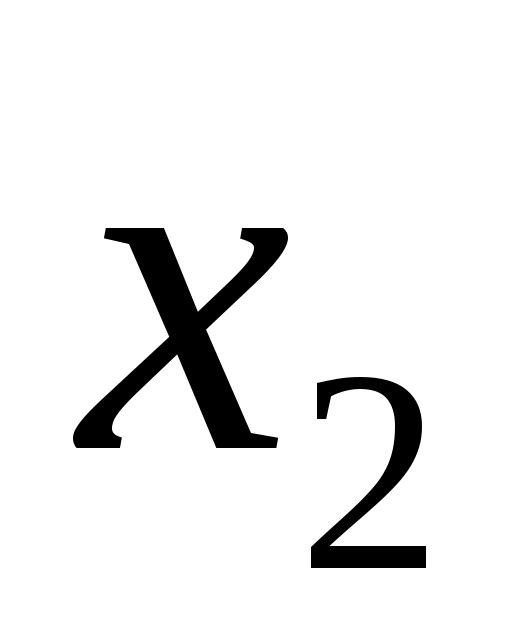 , …, , …, 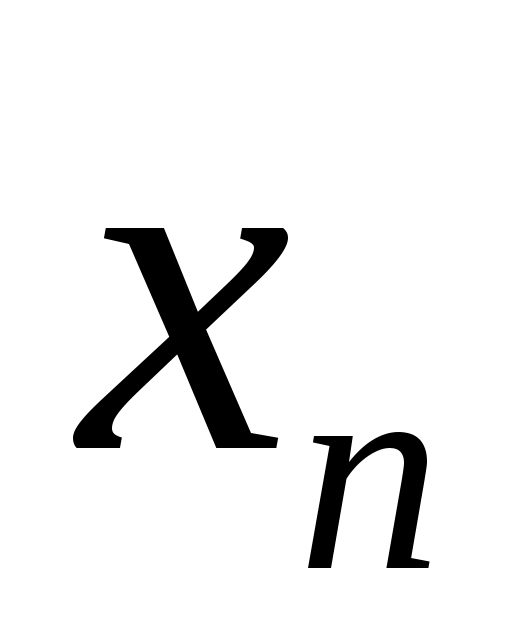 называются независимыми переменными или аргументами функции, а число u, соответствующее данной точке М, – частным значением функции в точке М. называются независимыми переменными или аргументами функции, а число u, соответствующее данной точке М, – частным значением функции в точке М.
ОПР. 12 Множество 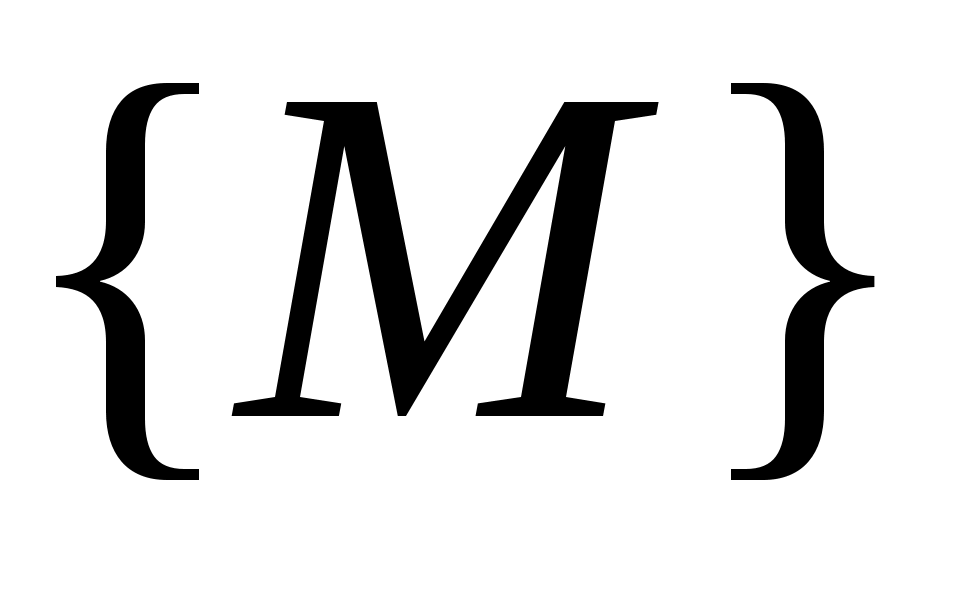 , состоящее из упорядоченных совокупностей n чисел, называется областью определения функции нескольких переменных (специальное обозначение: , состоящее из упорядоченных совокупностей n чисел, называется областью определения функции нескольких переменных (специальное обозначение: 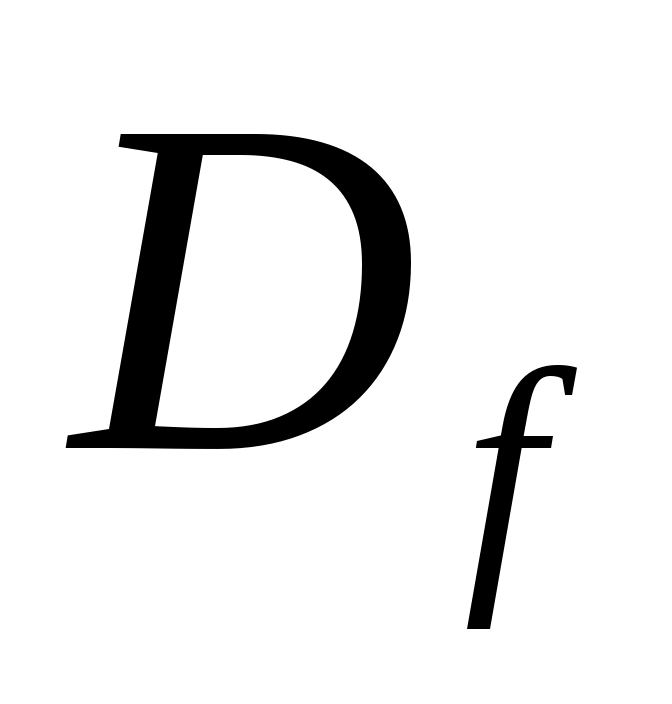 ), а множество ), а множество 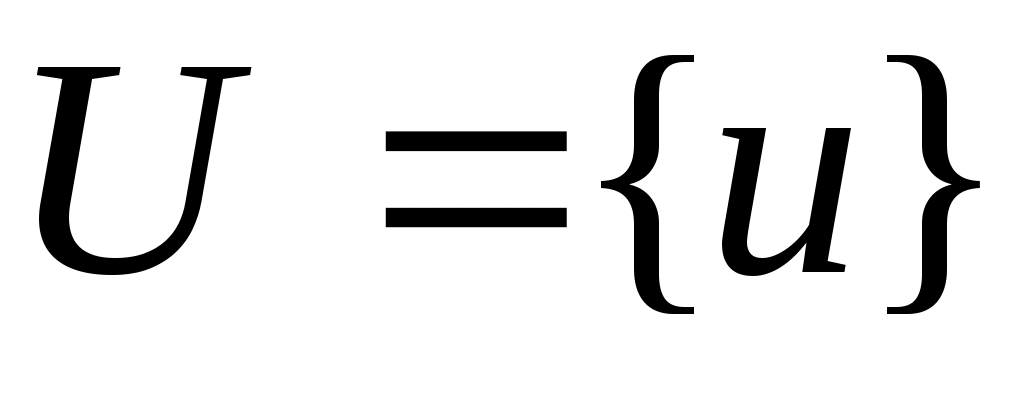 , в которое входят все частные значения функции , в которое входят все частные значения функции 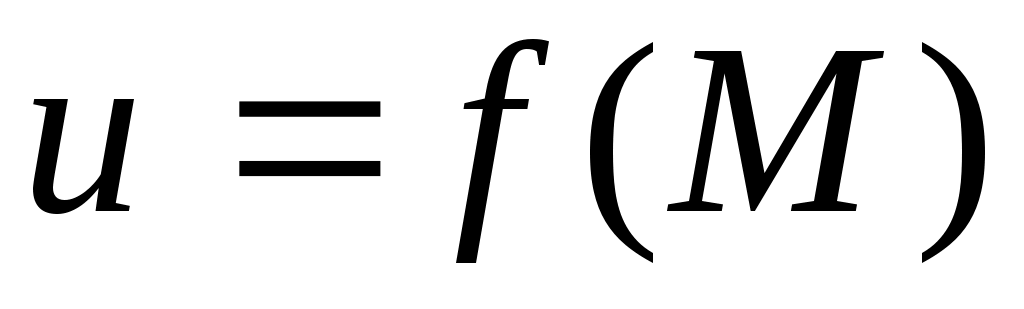 , где , где 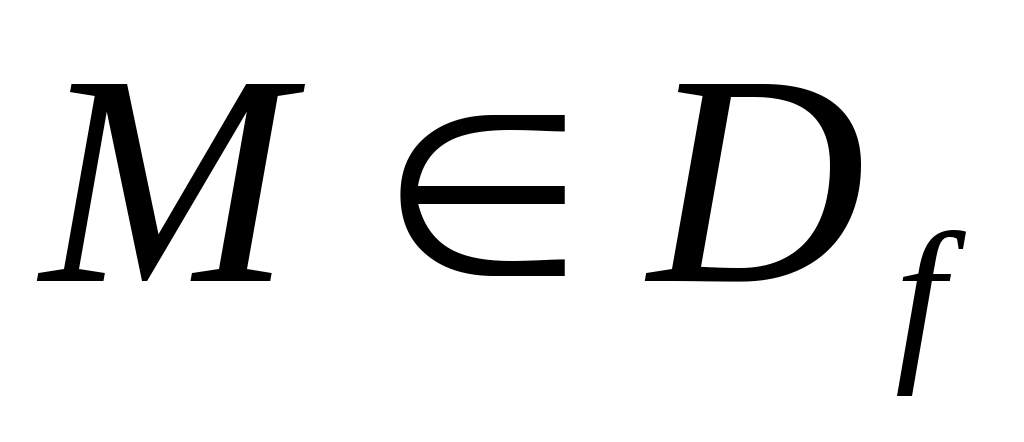 , – множеством значений этой функции. , – множеством значений этой функции.
ОПР. 13 Графиком функции 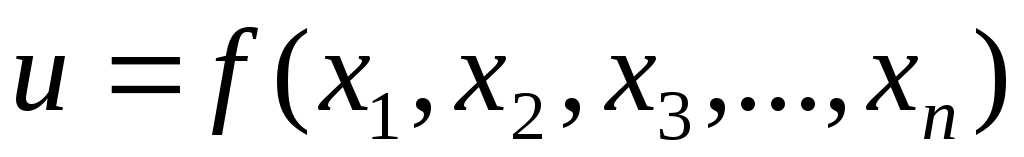 называется множество точек называется множество точек
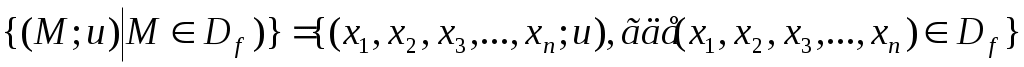 , ,
принадлежащих (n+ 1) – мерному пространству.
Замечание. Функции двух и трех переменных часто обозначают так: 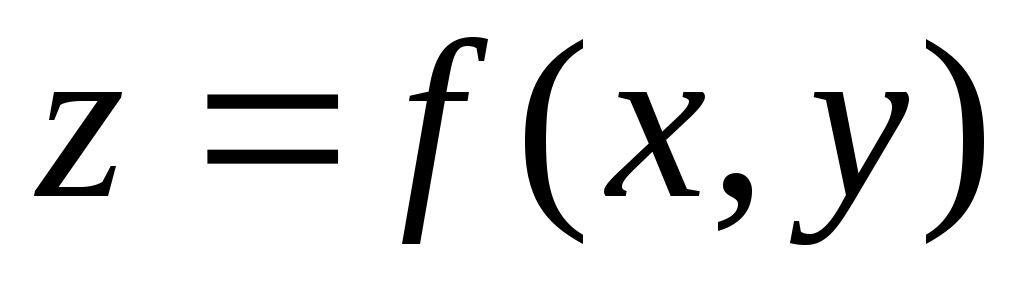 и и 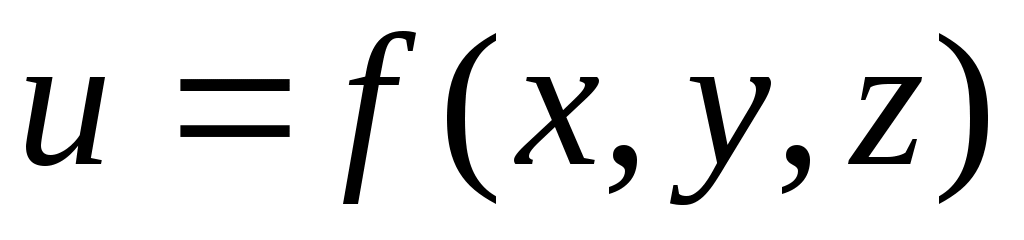 . Очевидно, что графиком функции . Очевидно, что графиком функции 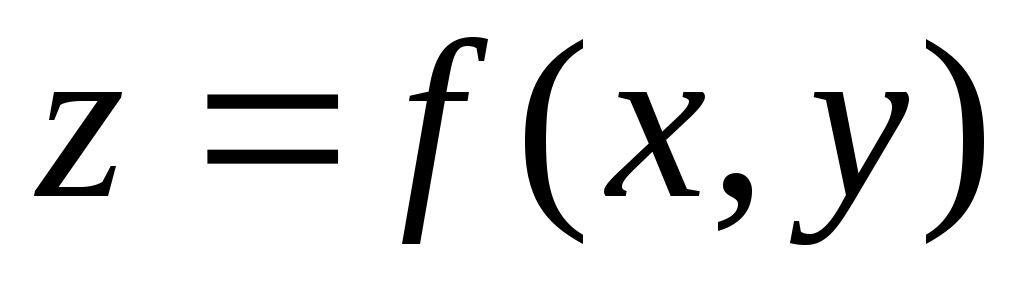 является некоторая поверхность в трехмерном пространстве, а для функций трех и большего числа переменных график построить нельзя. является некоторая поверхность в трехмерном пространстве, а для функций трех и большего числа переменных график построить нельзя.
Пример. Найти область определения и множество значений функции двух переменных 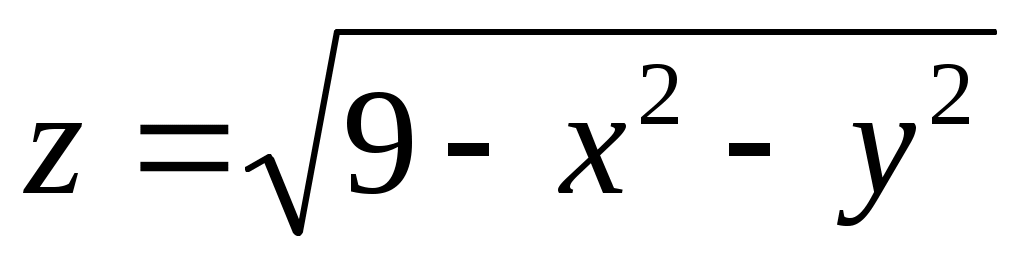 , выяснить вид ее графика. , выяснить вид ее графика.
РЕШЕНИЕ:
Функция принимает действительные значения при условии 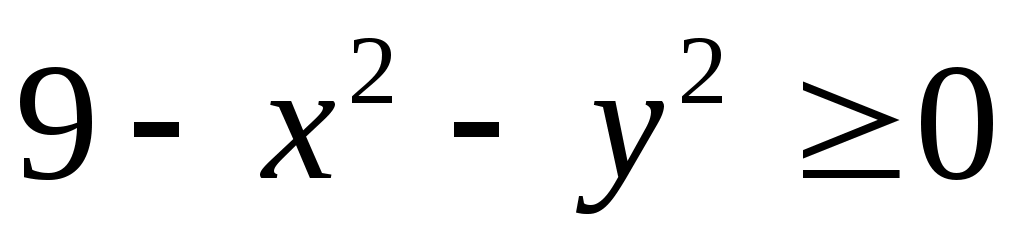 ,или ,или 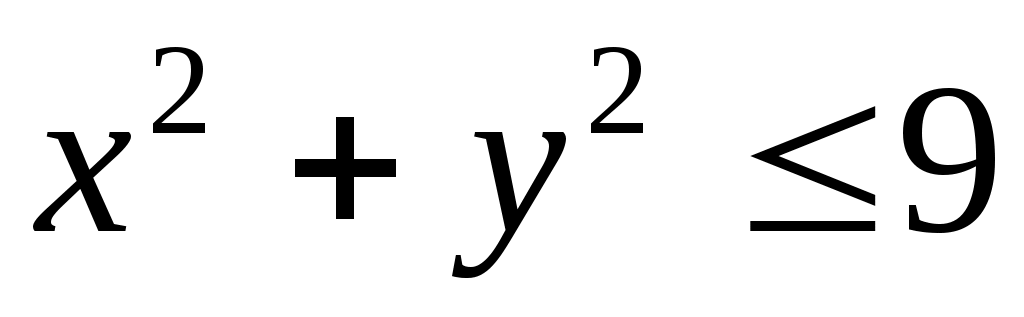 , т.е. областью определения данной функции является круг радиуса 3 с центром в начале координат, включая граничную окружность: , т.е. областью определения данной функции является круг радиуса 3 с центром в начале координат, включая граничную окружность: 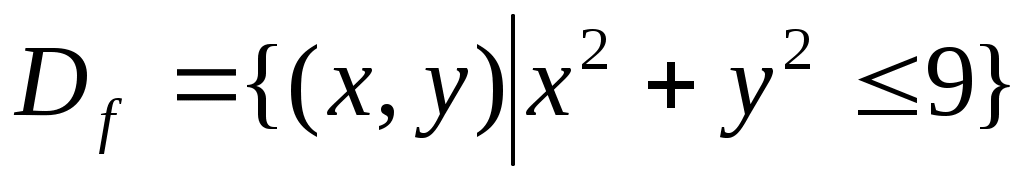 . Множеством значений функции является отрезок . Множеством значений функции является отрезок 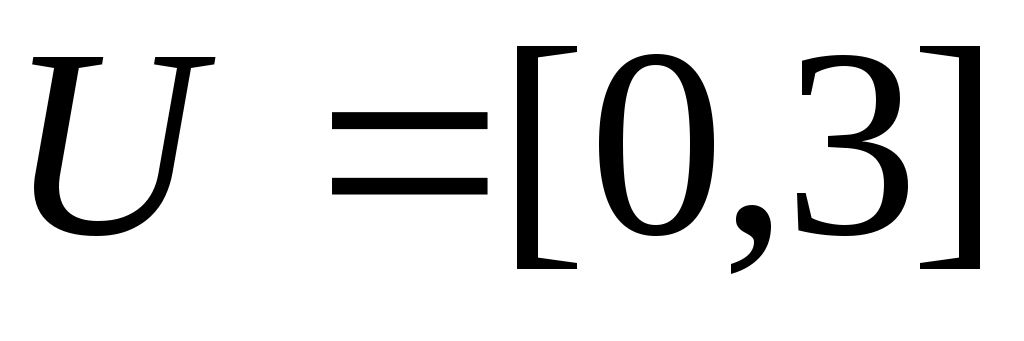 . Графиком функции . Графиком функции 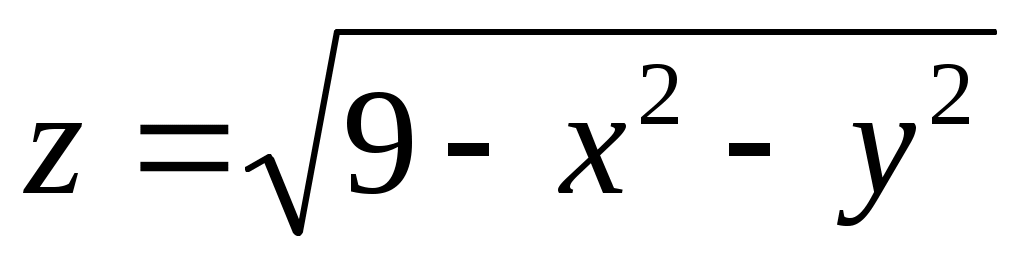 является верхняя половина сферы, заданной уравнением является верхняя половина сферы, заданной уравнением 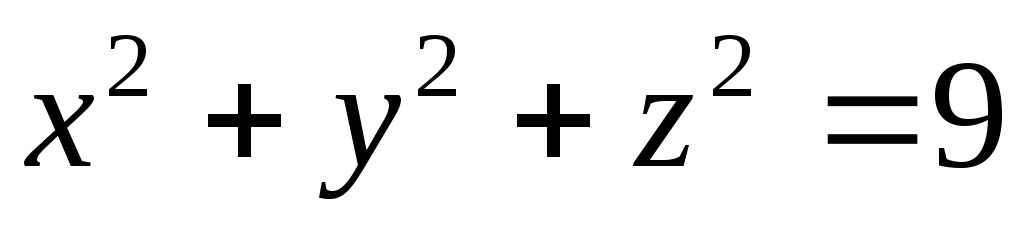 , удовлетворяющая условию , удовлетворяющая условию 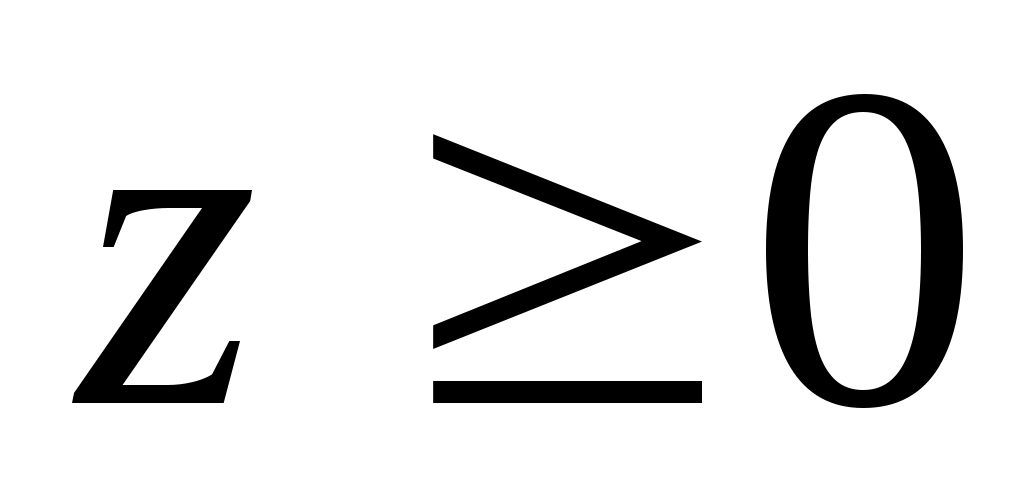 . .
ОПР. 14 Линией уровня функции двух переменных (скалярного поля) 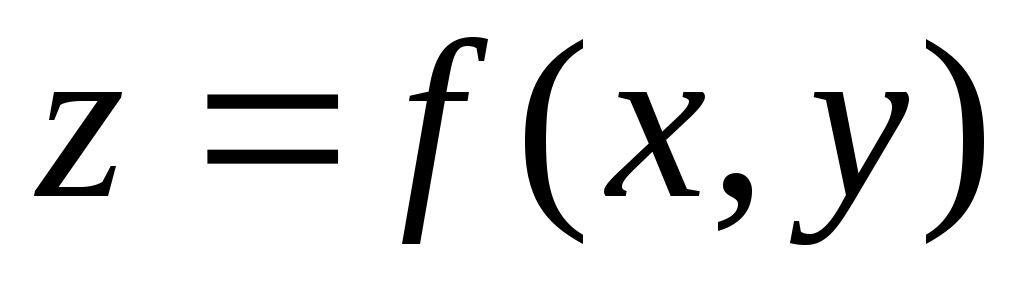 называется линия называется линия 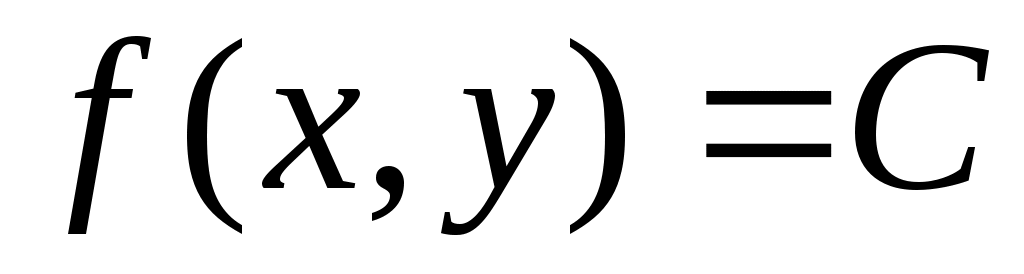 на плоскости на плоскости 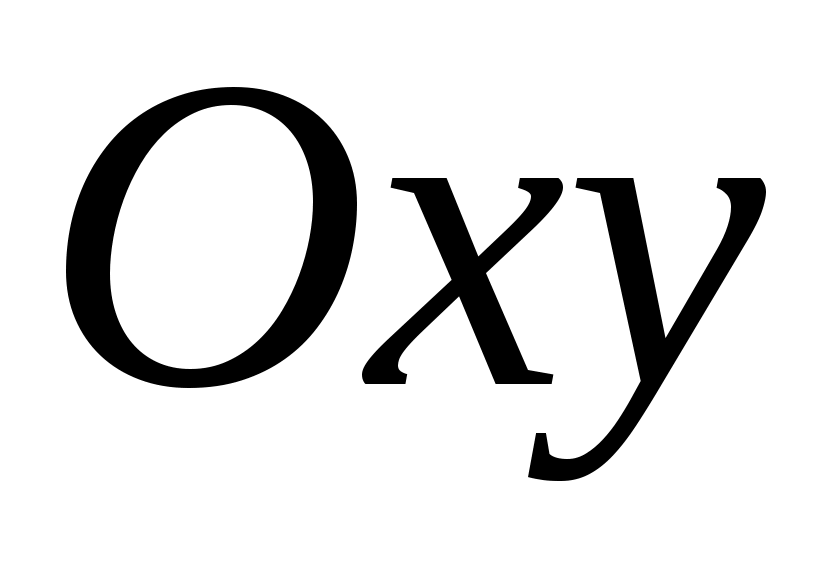 , во всех точках которой функция сохраняет постоянное значение , во всех точках которой функция сохраняет постоянное значение 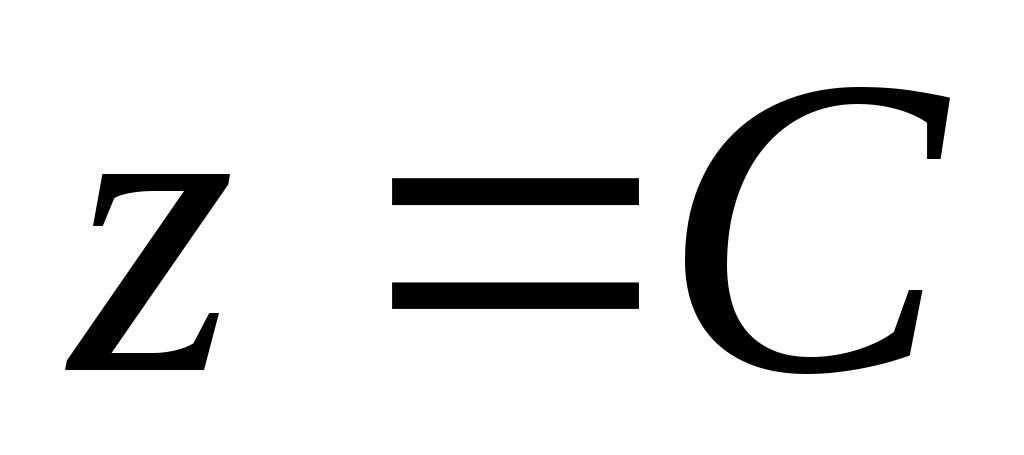 . Аналогично поверхностью уровня функции трех переменных (скалярного поля) . Аналогично поверхностью уровня функции трех переменных (скалярного поля) 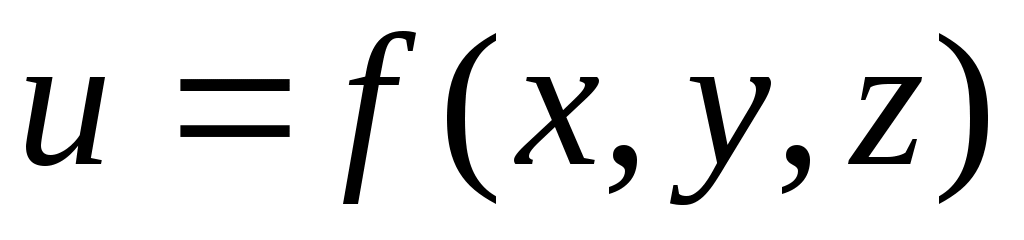 называется поверхность называется поверхность 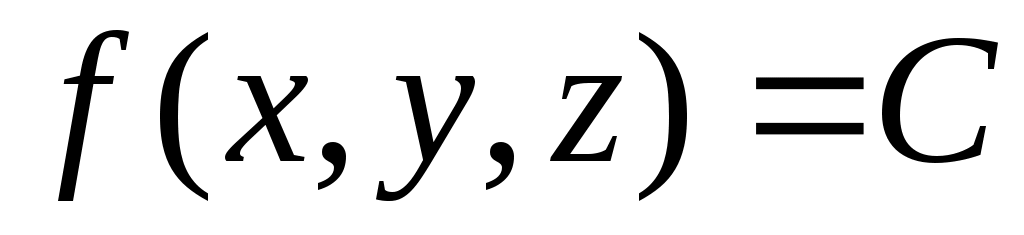 в координатном пространстве в координатном пространстве 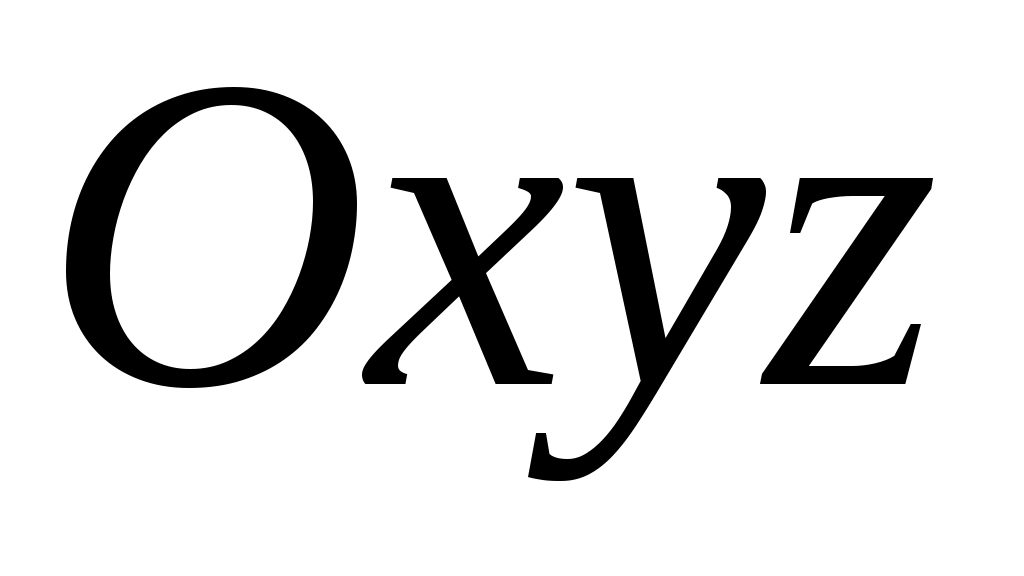 , в точках которой функция сохраняет постоянное значение , в точках которой функция сохраняет постоянное значение 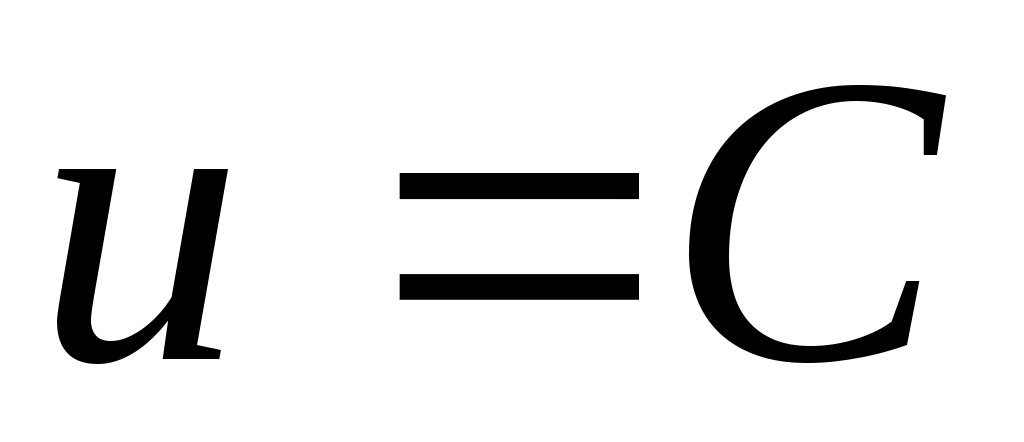 . .
Замечание. Известно, что для некоторых физических примеров скалярных полей (поле температур, поле давлений, поле потенциалов) существуют специальные названия линий или поверхностей уровня (изотермы, изобары, эквипотенциальные поверхности).
Пример. Указать линии уровня функции 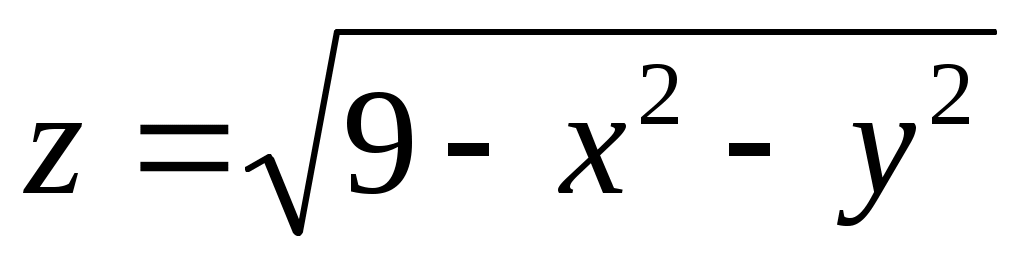 . .
РЕШЕНИЕ:
Уравнение множества линий уровня имеет вид 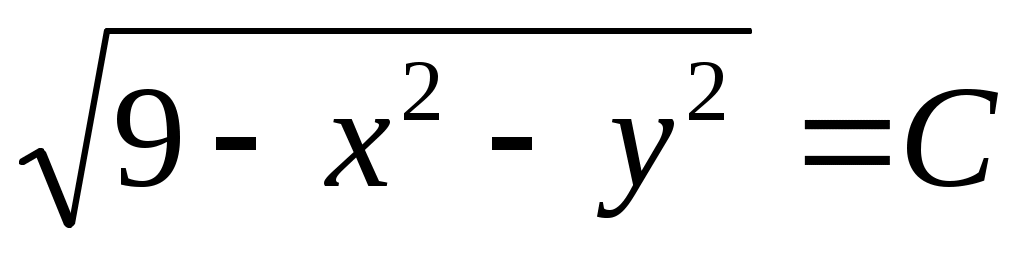 , или , или 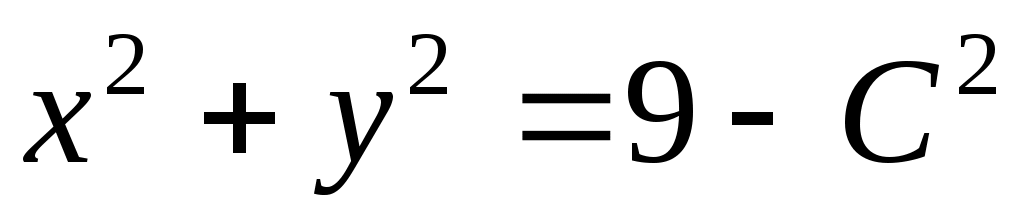 . Придавая постоянной С различные действительные значения, удовлетворяющие условию . Придавая постоянной С различные действительные значения, удовлетворяющие условию 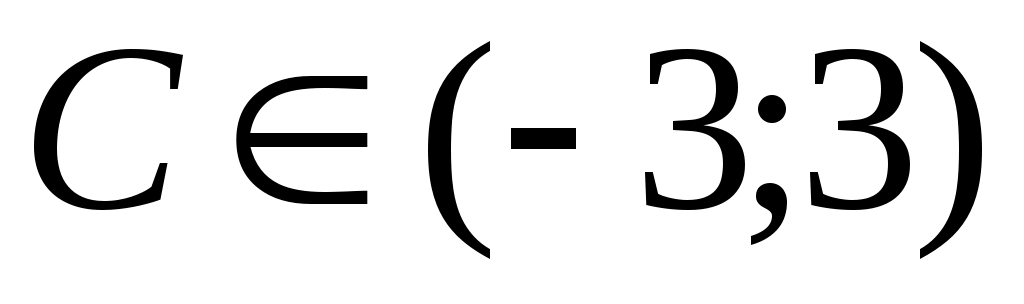 , получим семейство концентрических окружностей с центром в начале координат и радиусами, не превосходящими числа 3. , получим семейство концентрических окружностей с центром в начале координат и радиусами, не превосходящими числа 3.
Пример. Составить уравнение поверхности уровня функции 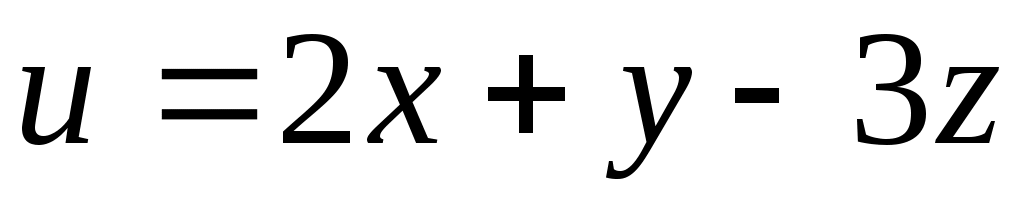 , проходящей через точку (3; –4; 2). , проходящей через точку (3; –4; 2).
РЕШЕНИЕ:
Уравнение множества поверхностей уровня имеет вид 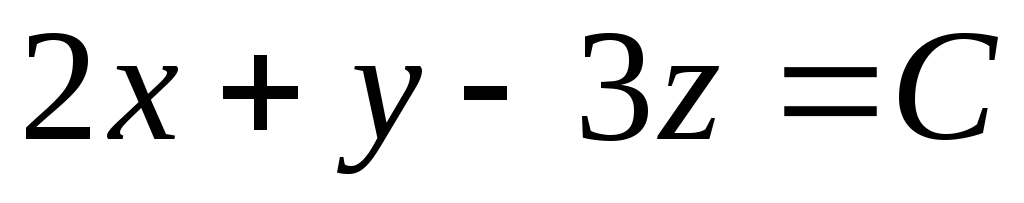 . Придавая постоянной С произвольные действительные значения, получим семейство параллельных между собой плоскостей, имеющих один и тот же нормальный вектор . Придавая постоянной С произвольные действительные значения, получим семейство параллельных между собой плоскостей, имеющих один и тот же нормальный вектор 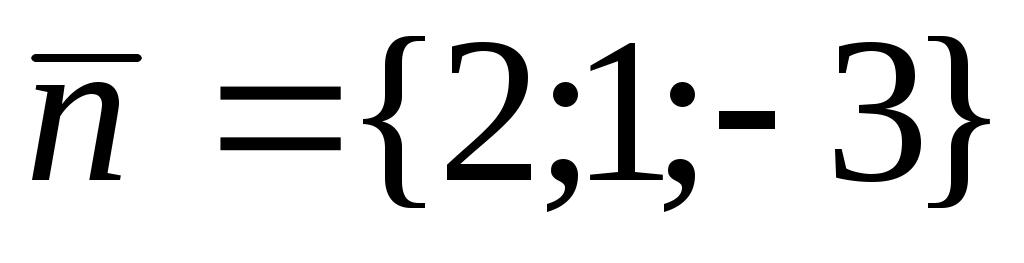 . Для поверхности, проходящей через заданную точку (3; –4; 2), получим, что С = –4, и уравнение соответствующей плоскости имеет вид . Для поверхности, проходящей через заданную точку (3; –4; 2), получим, что С = –4, и уравнение соответствующей плоскости имеет вид 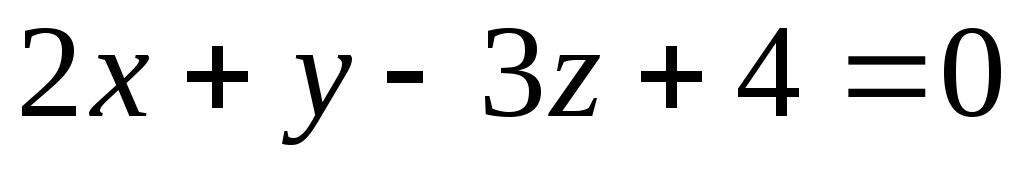 . .
III ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
Пусть функция 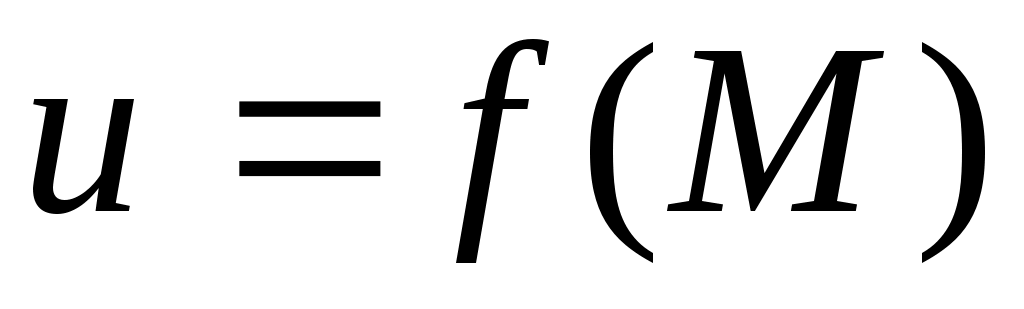 определена на множестве определена на множестве 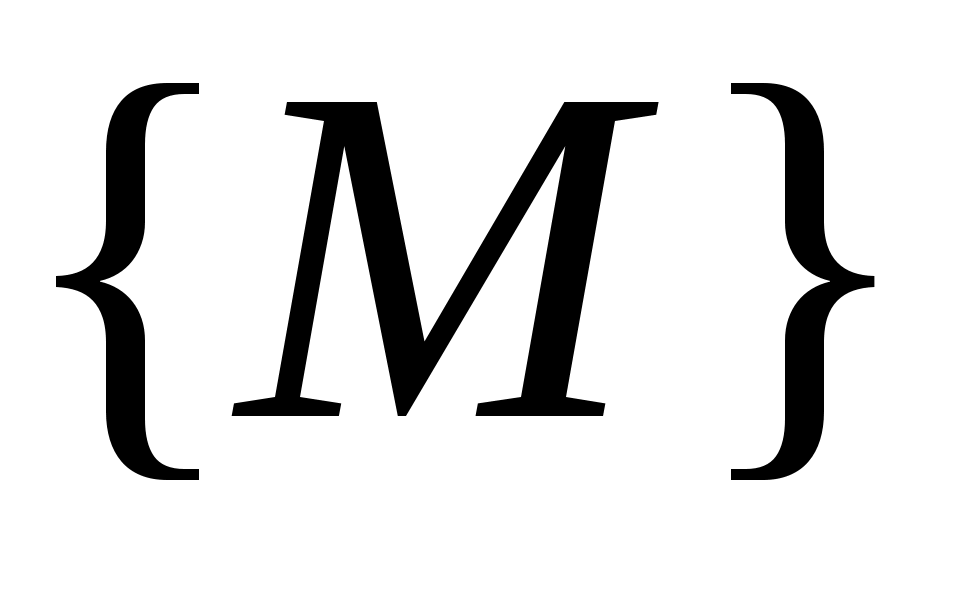 ( (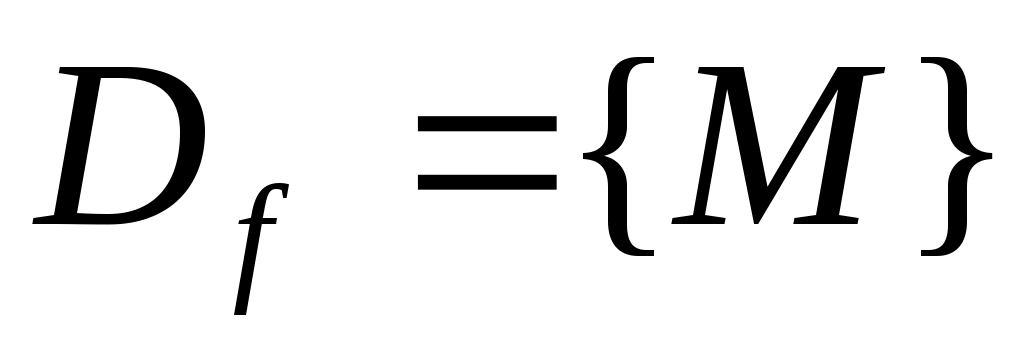 ) и точка ) и точка 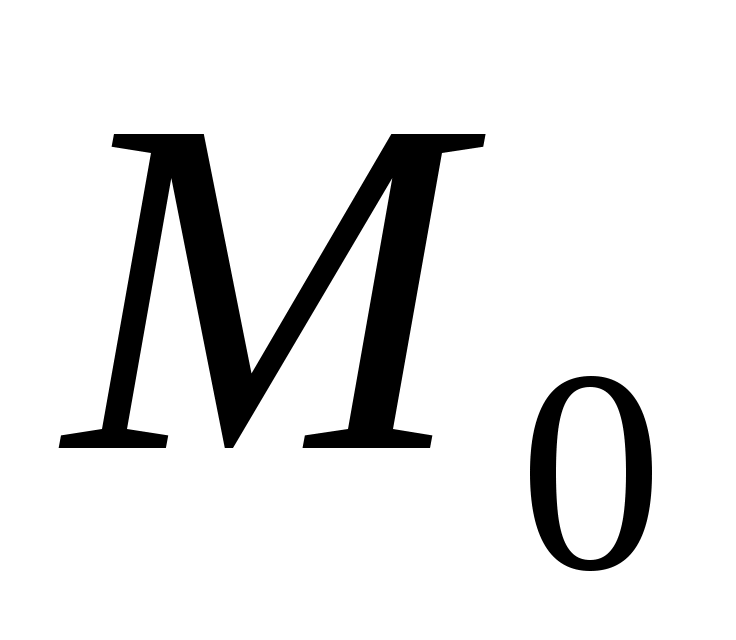 – предельная точка множества – предельная точка множества 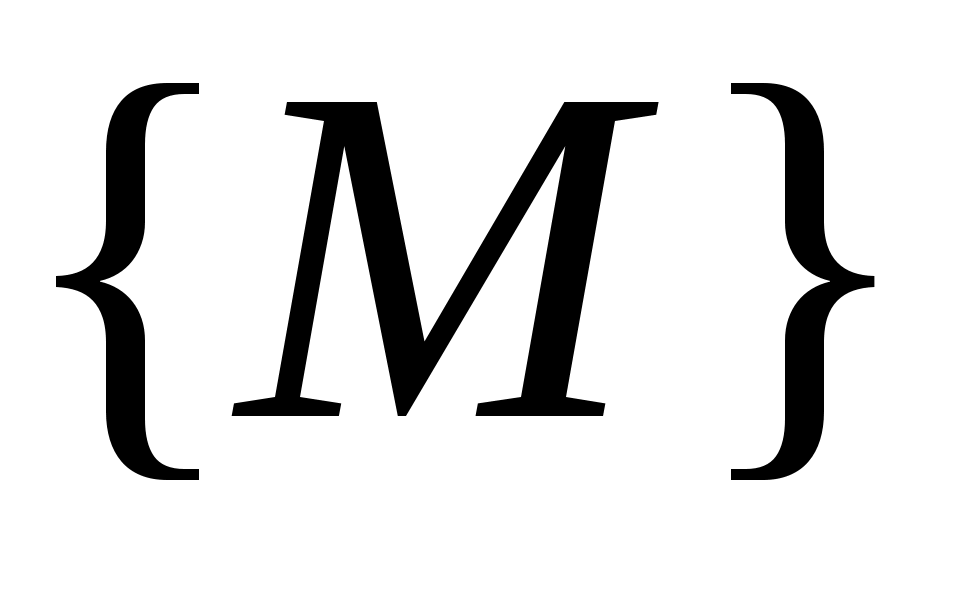 . Рассмотрим различные подходы к понятию предела функции нескольких переменных, выражаемые в двух эквивалентных друг другу определениях. . Рассмотрим различные подходы к понятию предела функции нескольких переменных, выражаемые в двух эквивалентных друг другу определениях.
ОПР. 15 (по Гейне). Число А называется пределомфункции 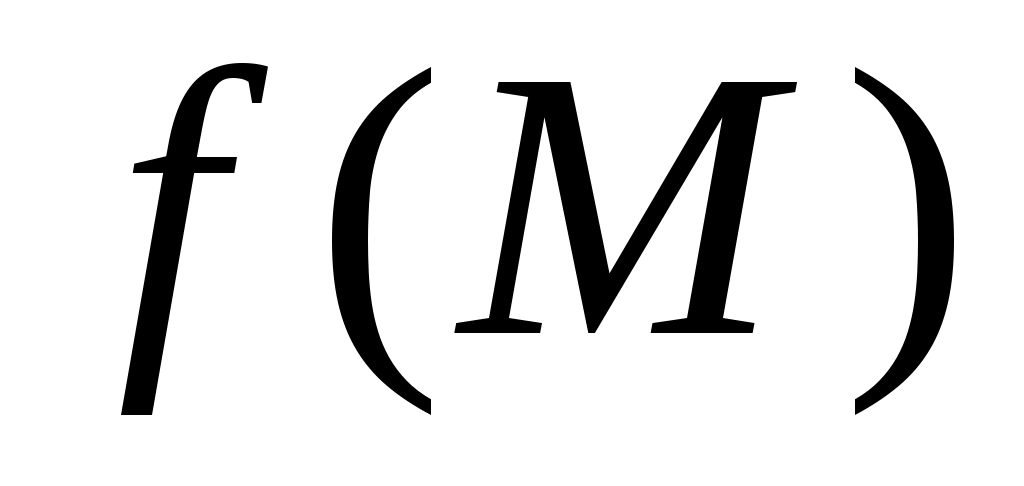 в точке в точке 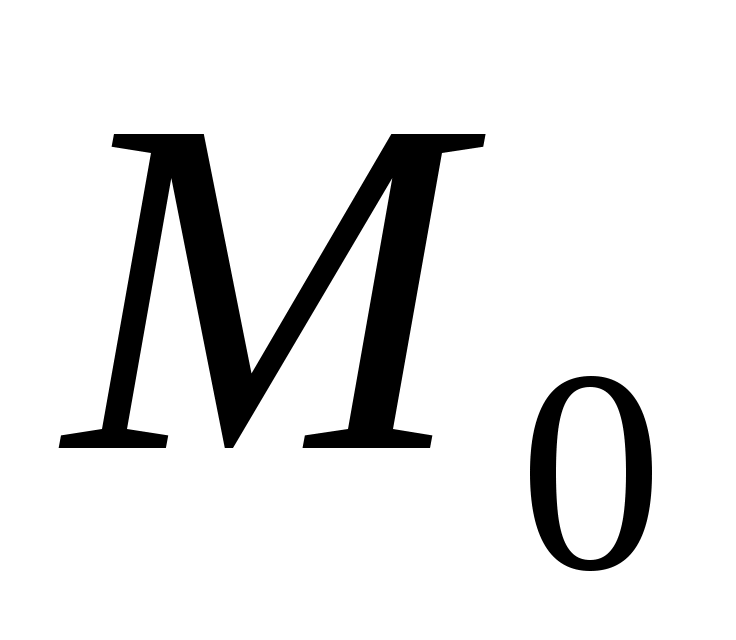 , если для любой сходящейся к , если для любой сходящейся к 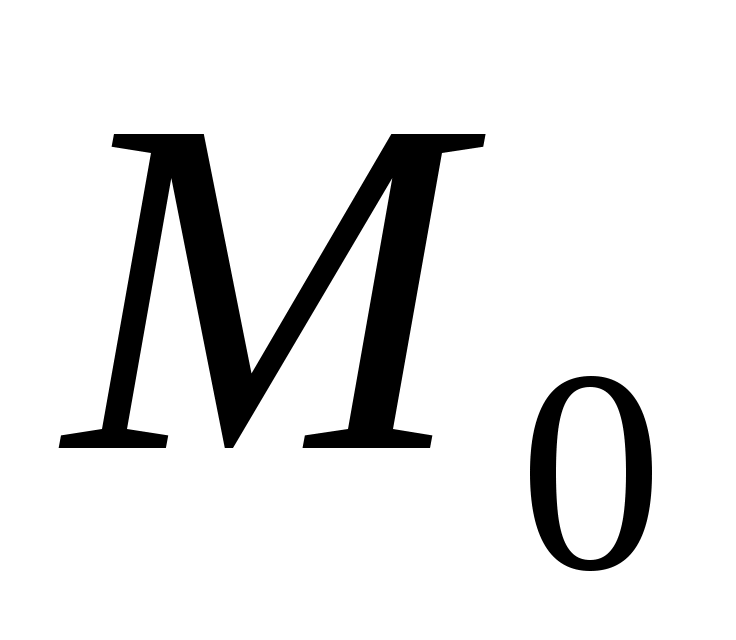 последовательности последовательности 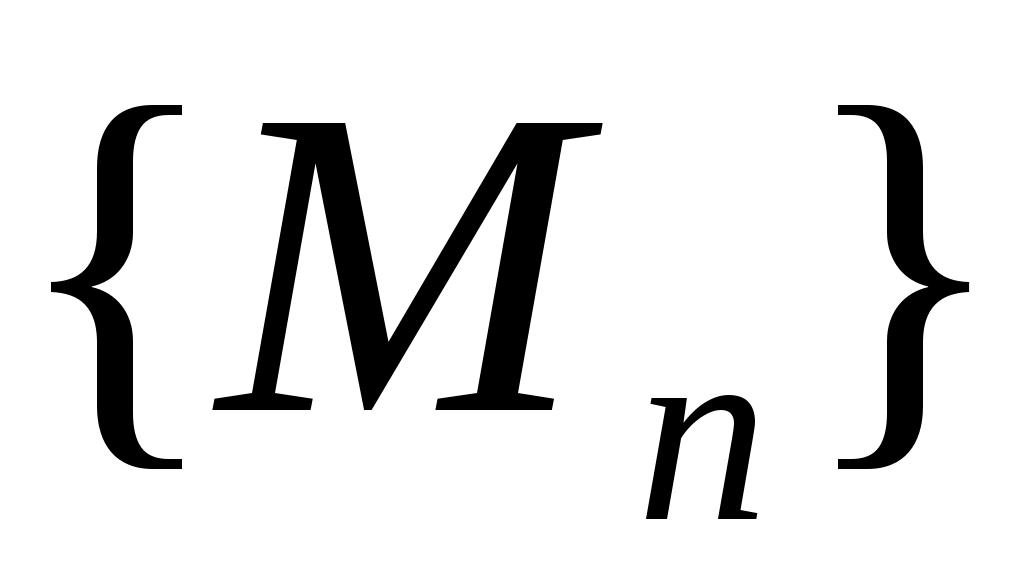 такой, что такой, что 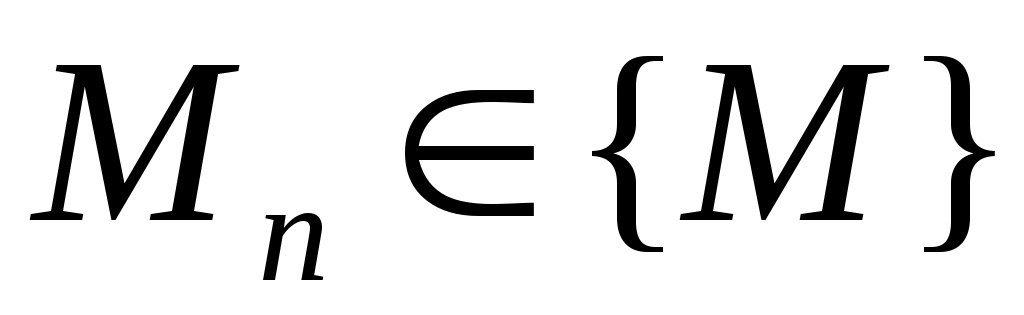 , , 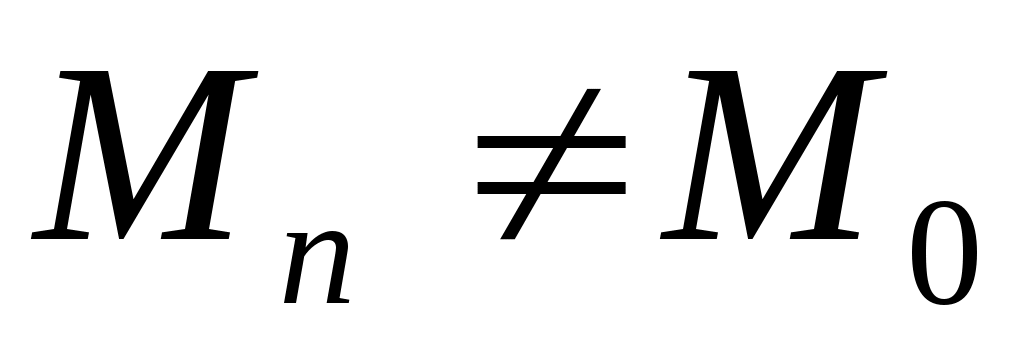 , соответствующая последовательность значений функции , соответствующая последовательность значений функции 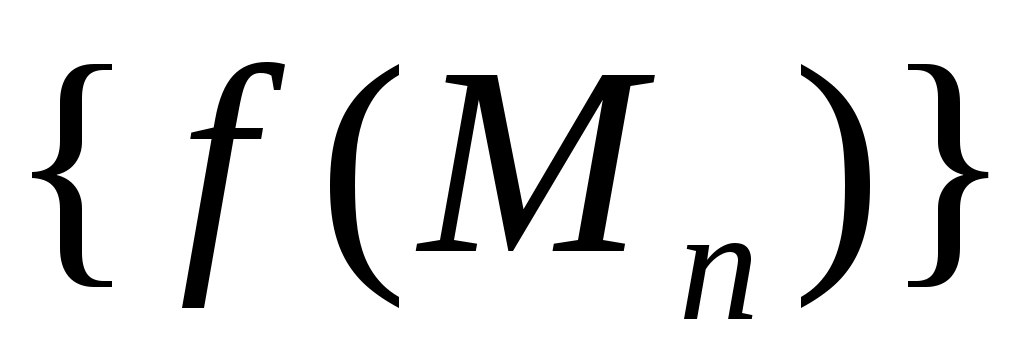 сходится к числу А: сходится к числу А:
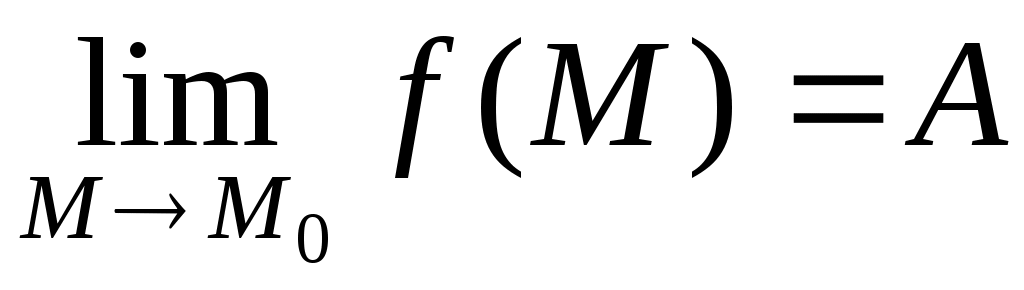 или или 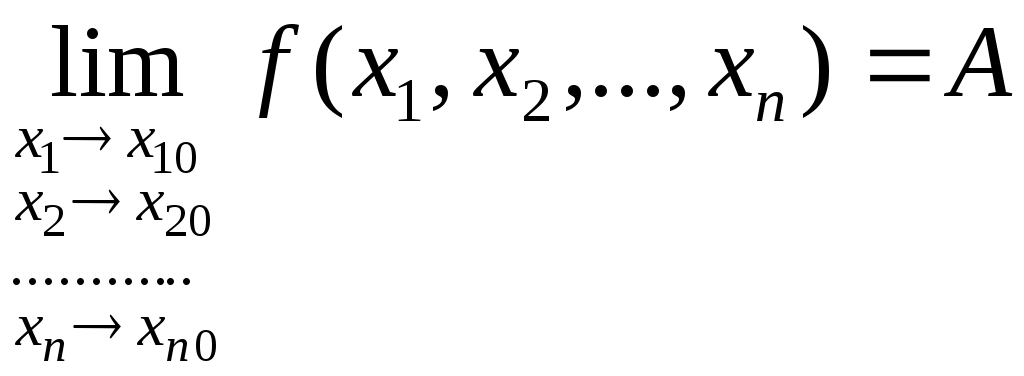 . 6 . 6
ОПР. 16 (по Коши). Число А называется пределомфункции 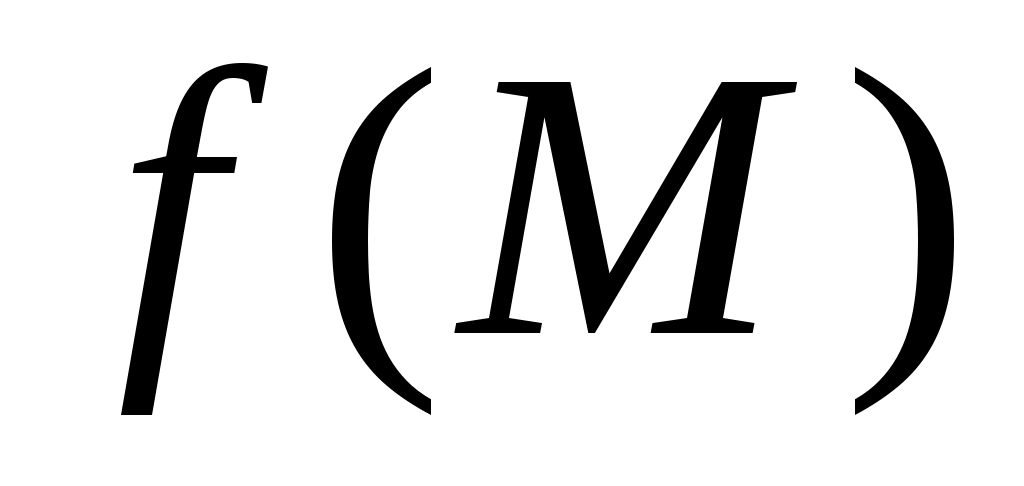 в точке в точке 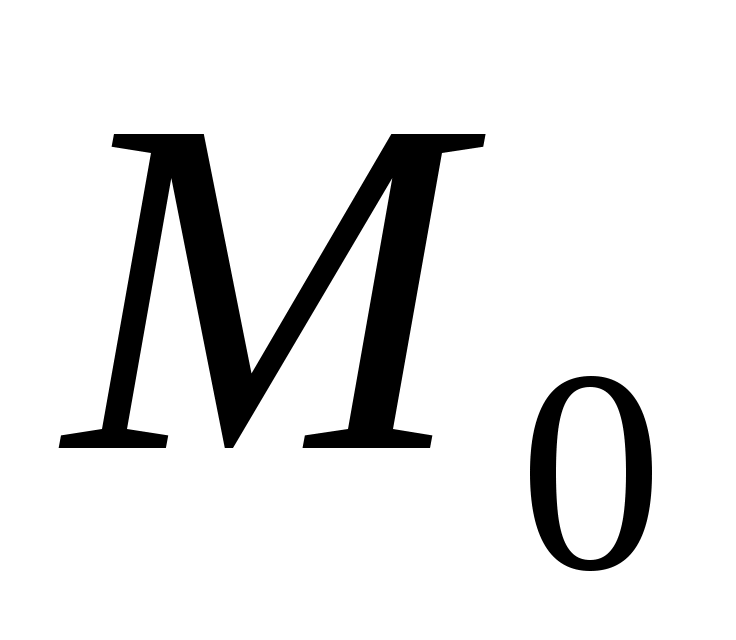 (при (при 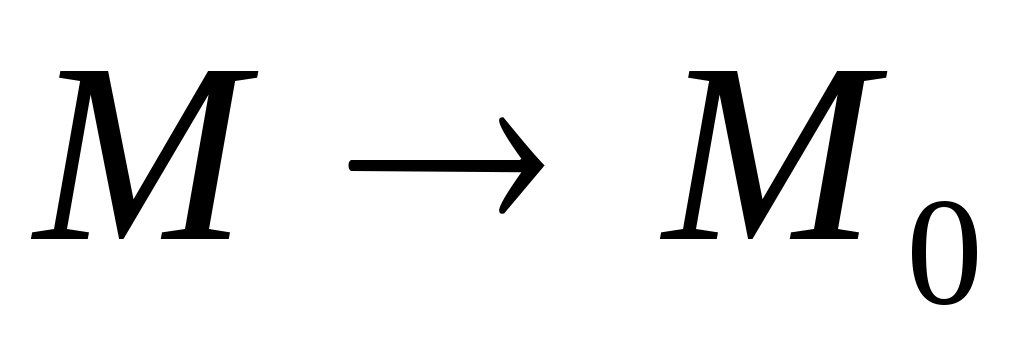 ), если для любого сколь угодно малого числа ), если для любого сколь угодно малого числа 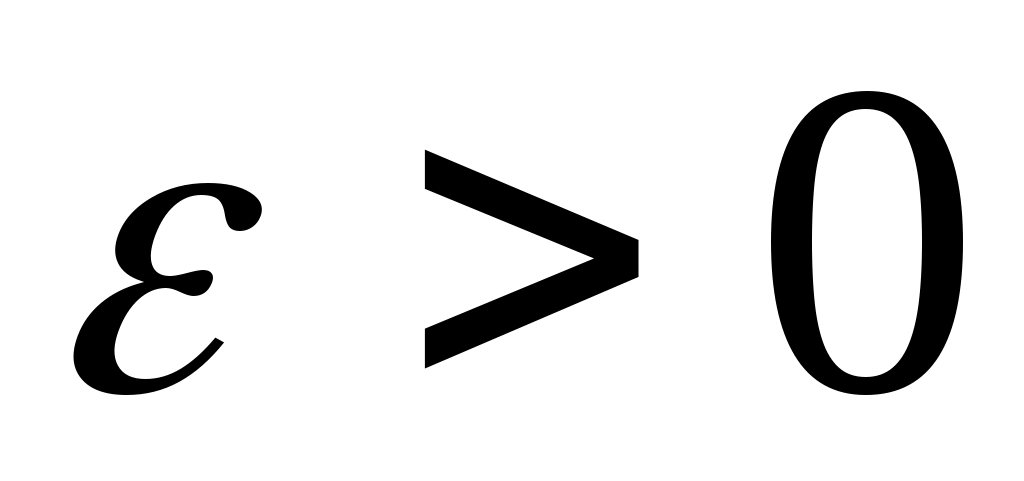 найдется такое число найдется такое число 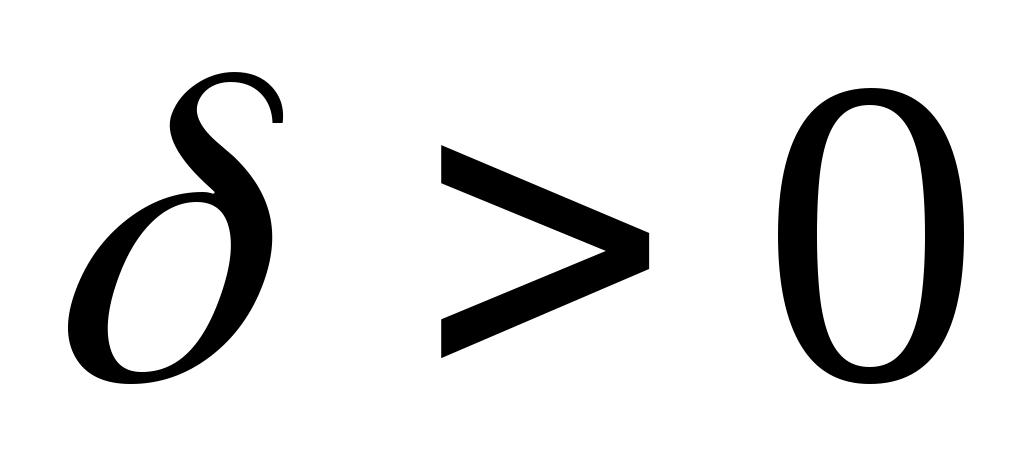 , что для всех точек , что для всех точек 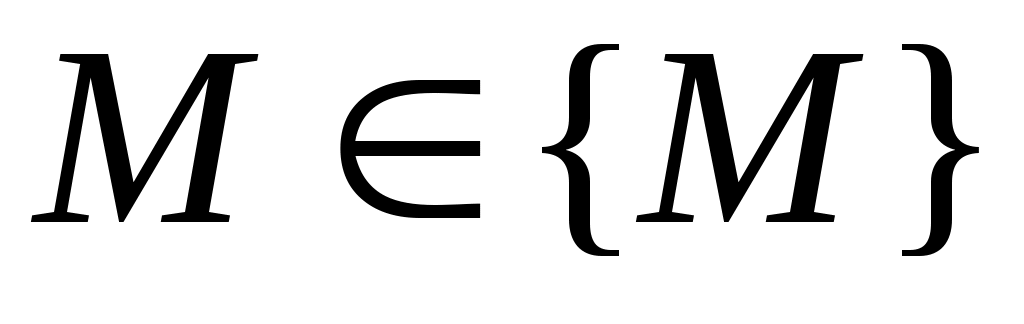 , удовлетворяющих условию , удовлетворяющих условию 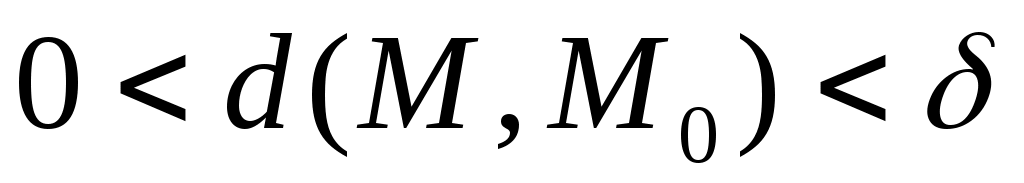 , выполняется неравенство , выполняется неравенство 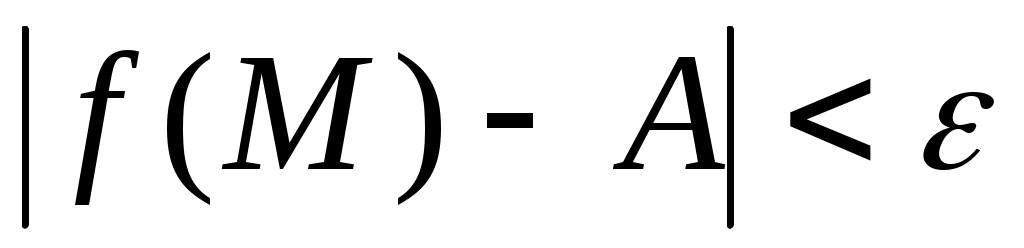 . .
Замечание. Число А является пределом, например, функции трех переменных 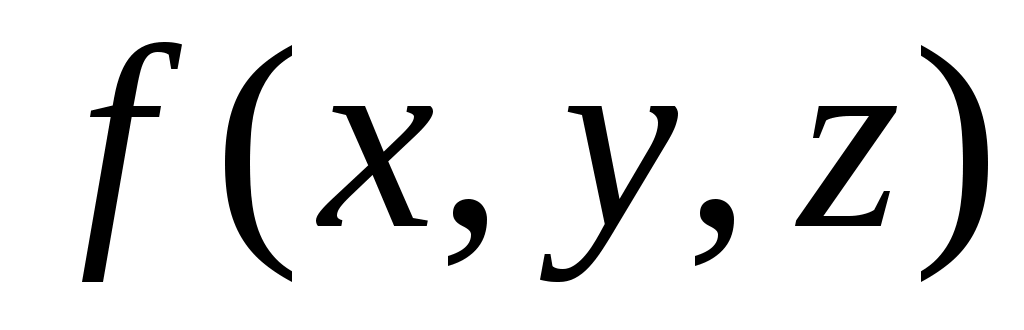 в точке в точке 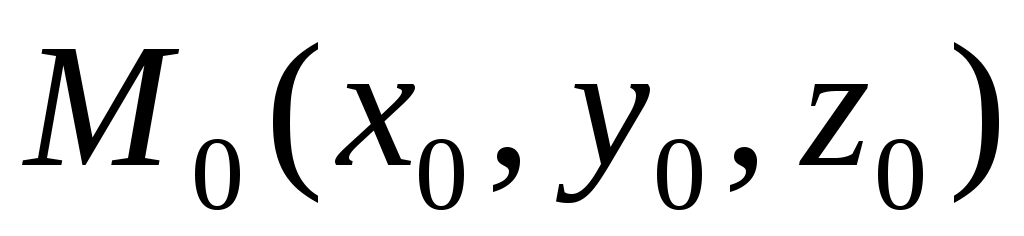 , если для всех значений x, yи z, достаточно мало отличающихся от чисел x0, y0 и z0, соответствующие значения функции , если для всех значений x, yи z, достаточно мало отличающихся от чисел x0, y0 и z0, соответствующие значения функции 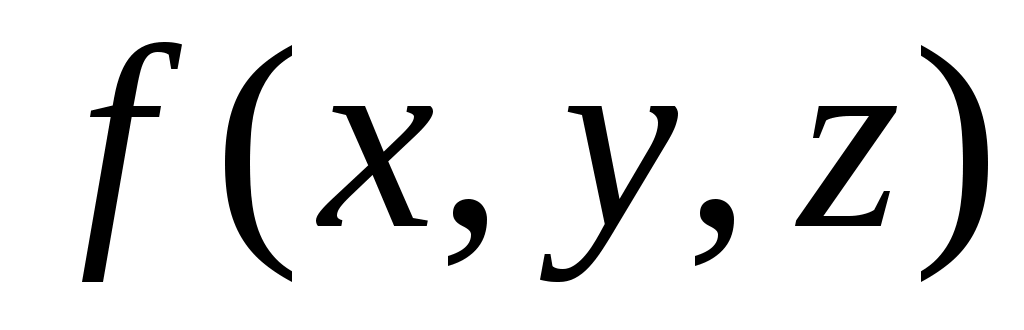 как угодно мало отличаются от числа А: как угодно мало отличаются от числа А:
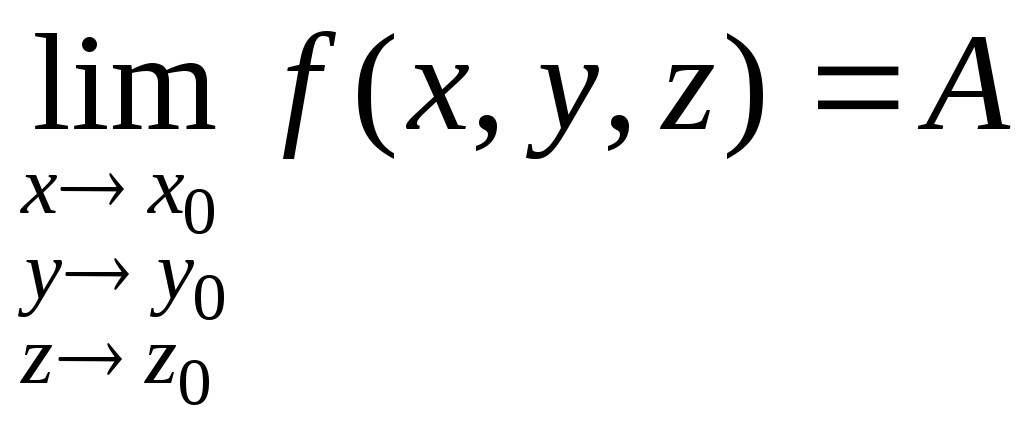 . 7 . 7
Пусть функция 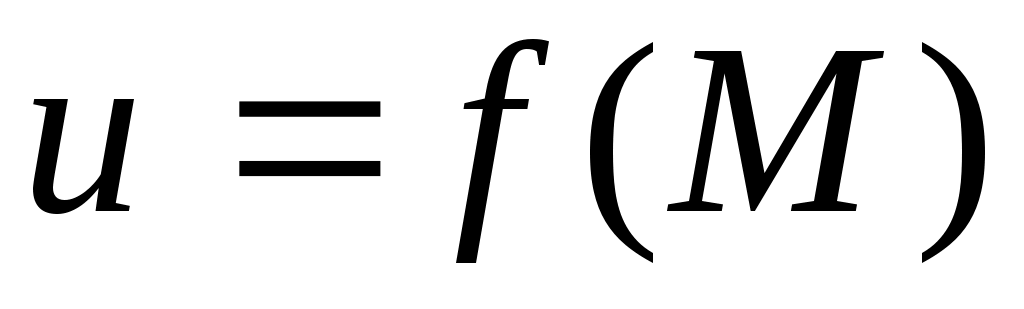 определена на множестве определена на множестве 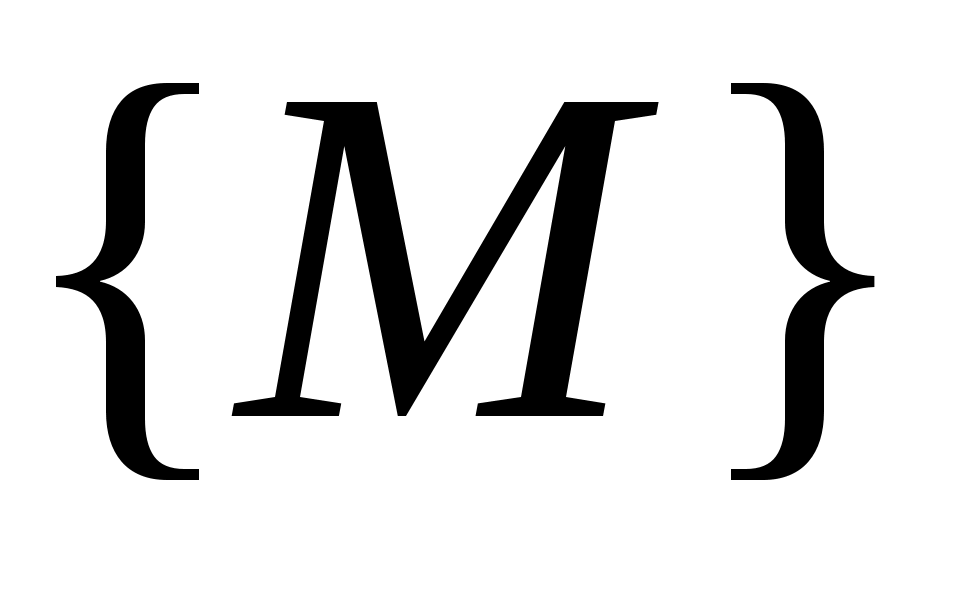 , которое содержит точки, сколь угодно удаленные от точки , которое содержит точки, сколь угодно удаленные от точки 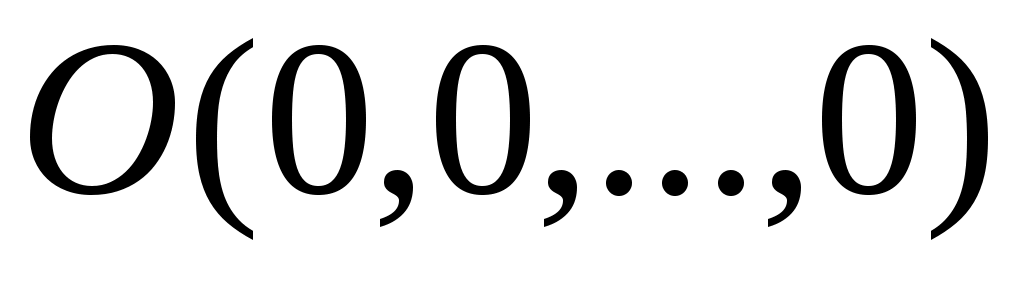 . .
Все правила предельного перехода, рассмотренные для функций одной переменной, без всяких изменений переносятся на случай функций нескольких переменных.
ОПР. 17 Функция 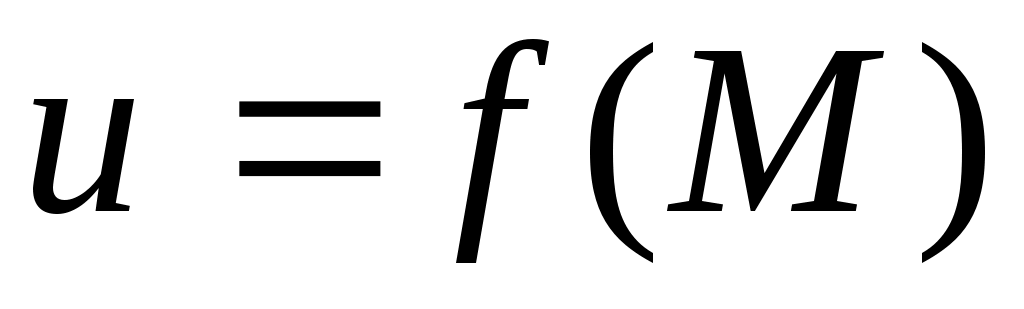 называется непрерывной в точке называется непрерывной в точке 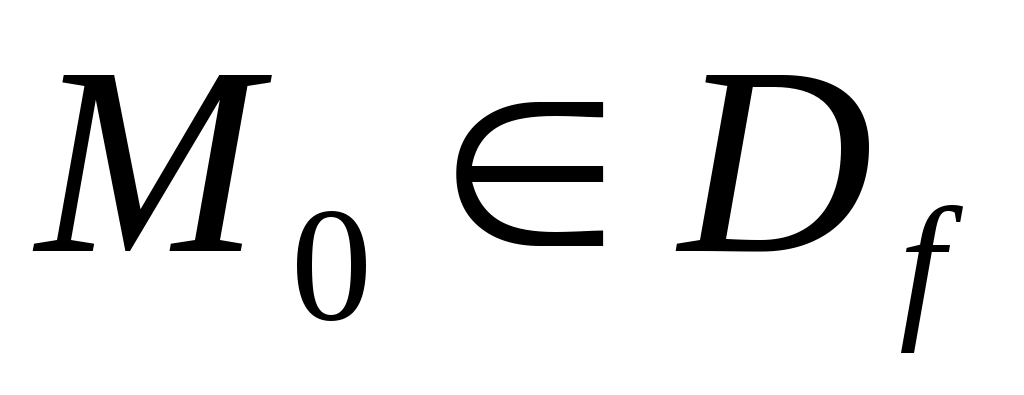 , если она определена в некоторой окрестности этой точки (т.е. точка , если она определена в некоторой окрестности этой точки (т.е. точка 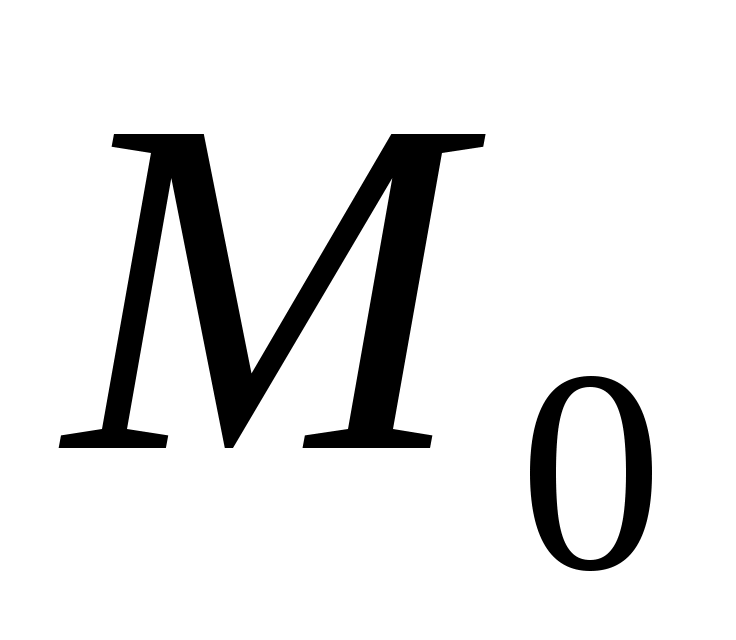 является внутренней точкой является внутренней точкой 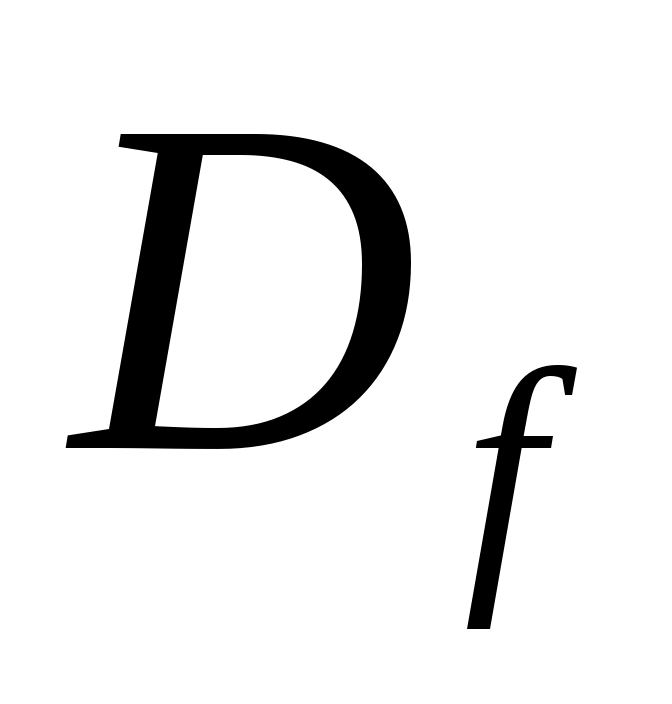 ) и ее предел равен значению функции в предельной точке: ) и ее предел равен значению функции в предельной точке:
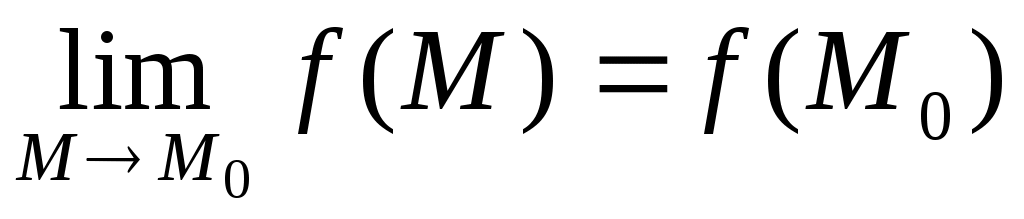 . 8 . 8
Для функции трех переменных 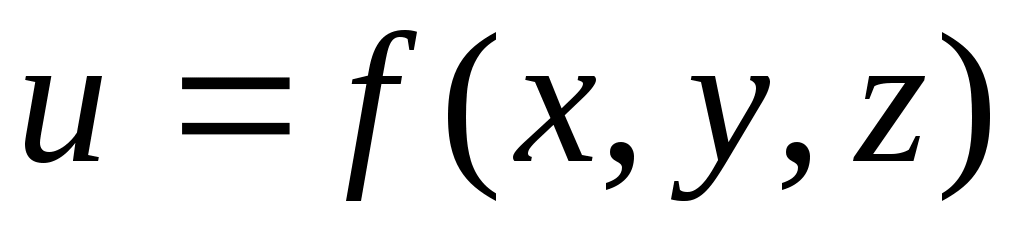 и внутренней точки и внутренней точки 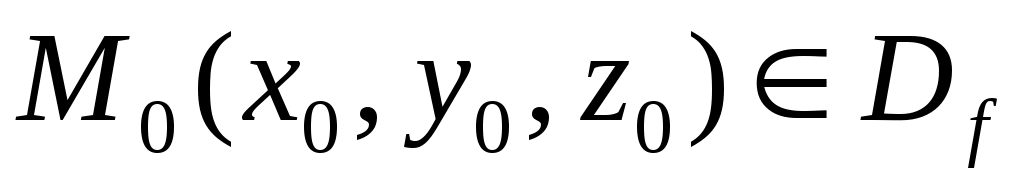 равенство 7 примет вид: равенство 7 примет вид:
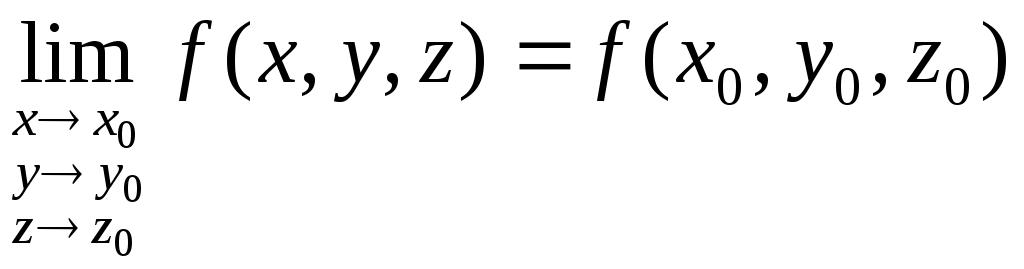 . 9 . 9
Замечание. Аналогично соответствующим положениям теории функций одной переменной арифметические операции над непрерывными в данной точке функциями нескольких переменных, так же, как и построение сложных функций, приводят к непрерывным же функциям.
ОПР. 18 Функция, непрерывная в каждой точке некоторой области 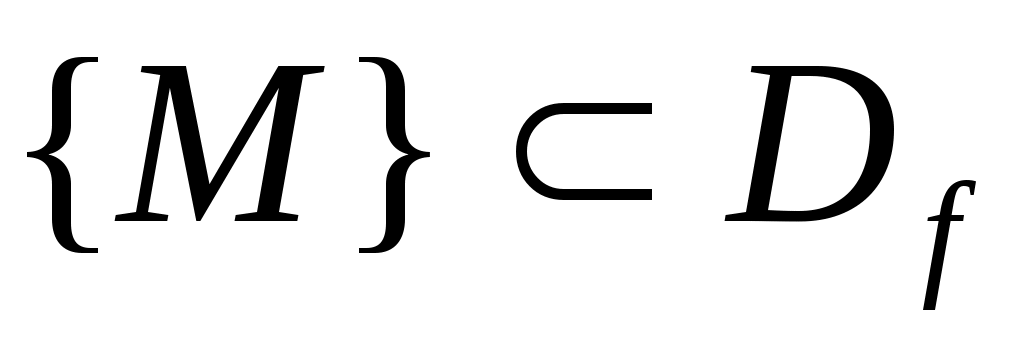 , называется непрерывной в этой области. , называется непрерывной в этой области.
Отметим свойства, характерные для непрерывных в замкнутых ограниченных областях функций нескольких переменных.
Если функция 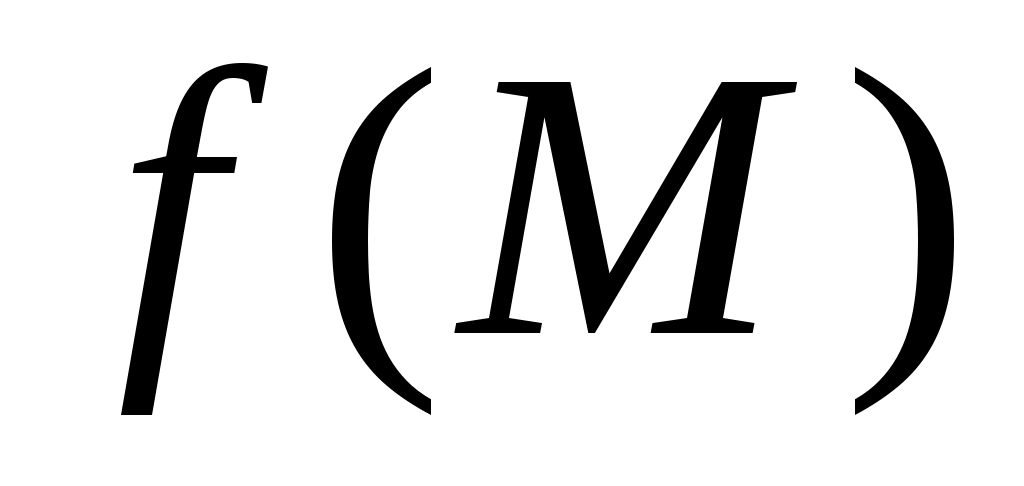 непрерывна в замкнутой ограниченной области непрерывна в замкнутой ограниченной области 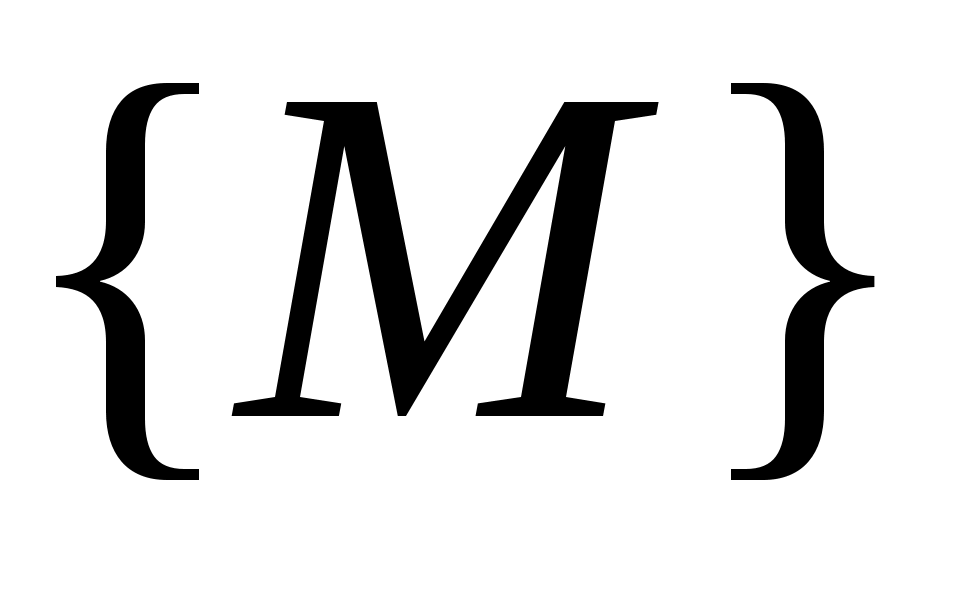 , то: , то:
функция 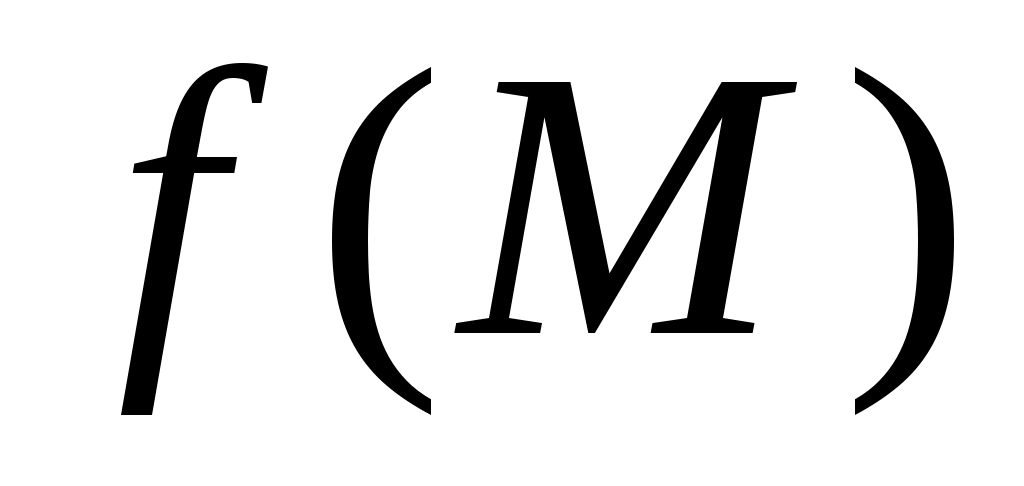 ограничена в области ограничена в области 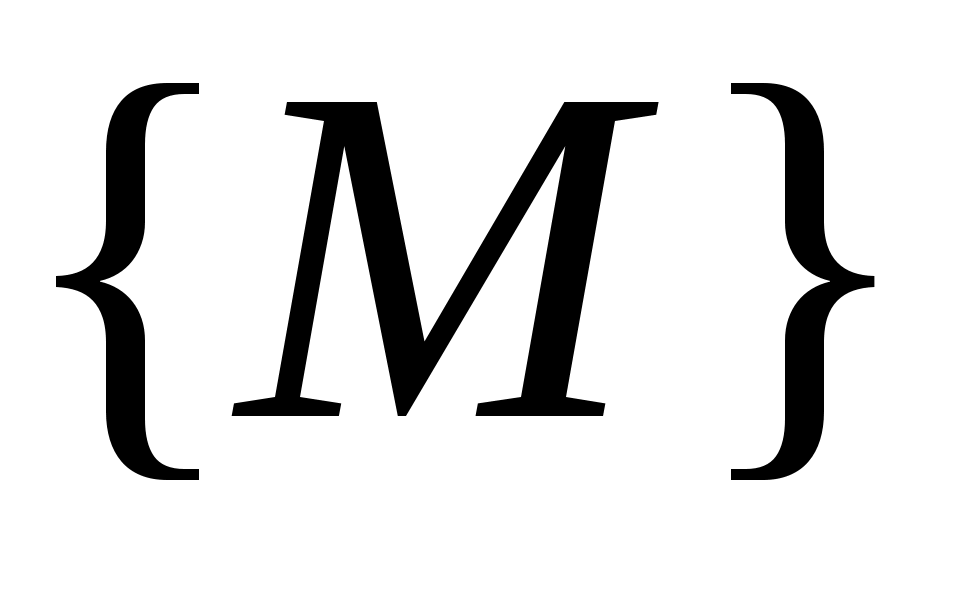 ; ;
функция 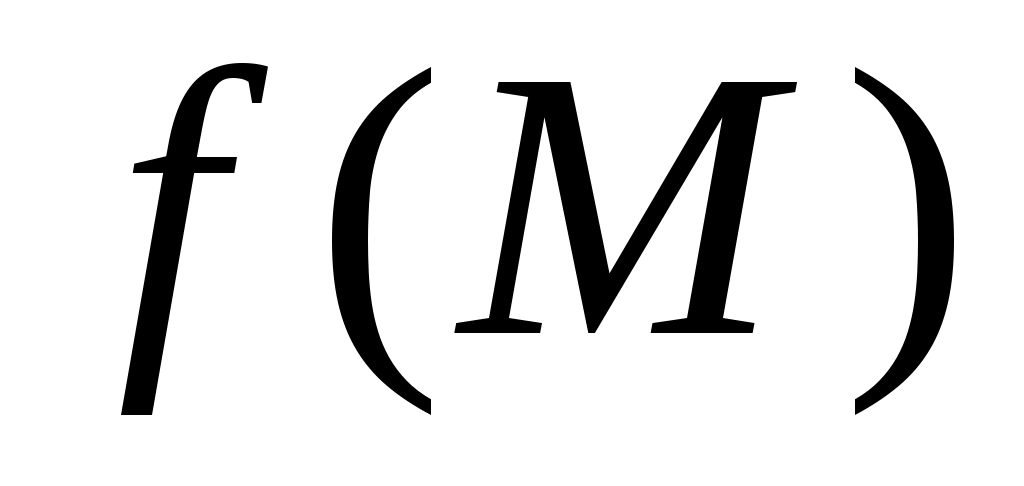 принимает в принимает в 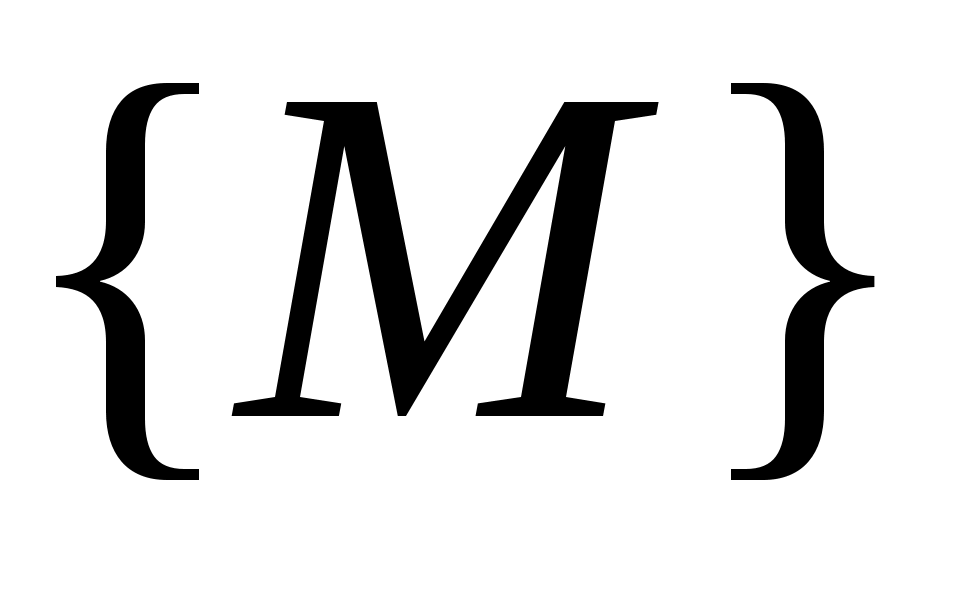 свои наименьшее и наибольшее значения; свои наименьшее и наибольшее значения;
функция 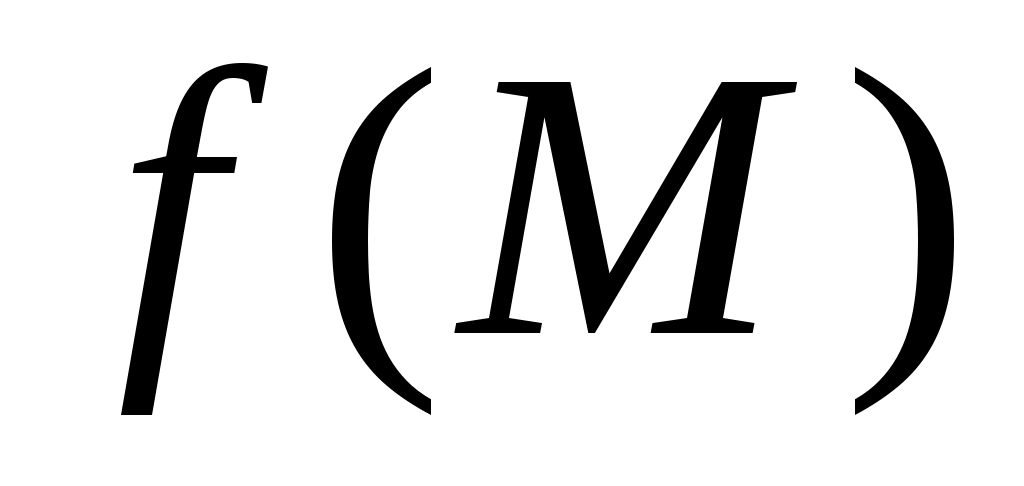 принимает в принимает в 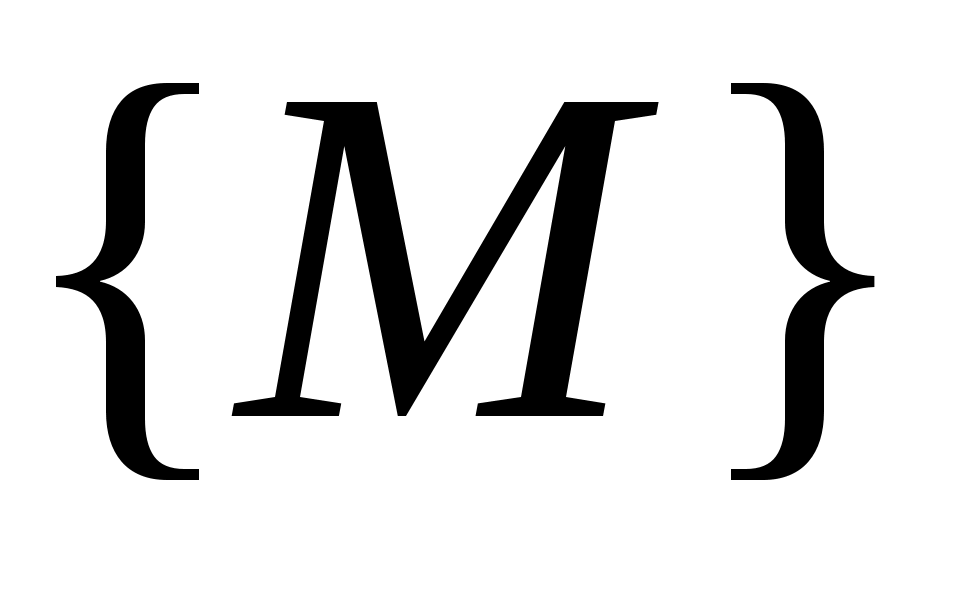 любое значение, заключенное между наименьшим и наибольшим значениями. любое значение, заключенное между наименьшим и наибольшим значениями.
ОПР. 19 Предельные точки области определения функции 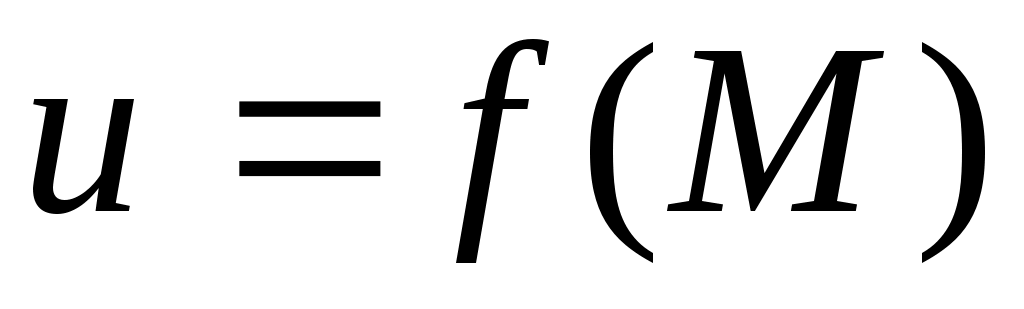 , в которых функция не является непрерывной, называются точками разрыва этой функции. , в которых функция не является непрерывной, называются точками разрыва этой функции.
|
 Скачать 336.5 Kb.
Скачать 336.5 Kb.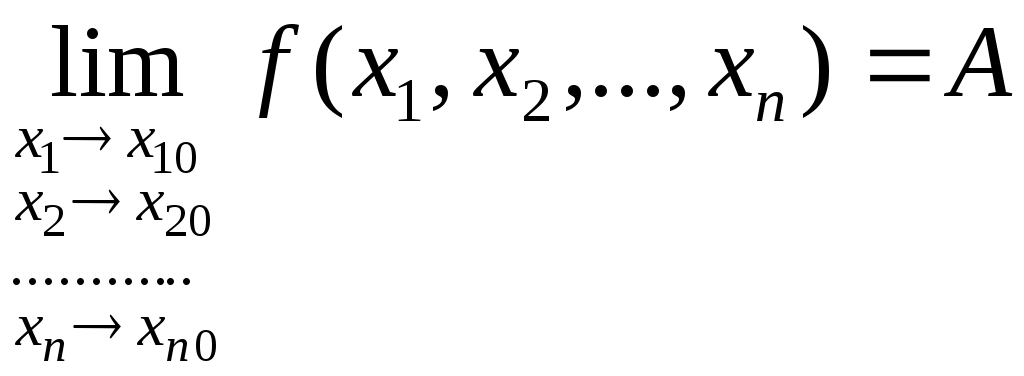 . 6
. 6 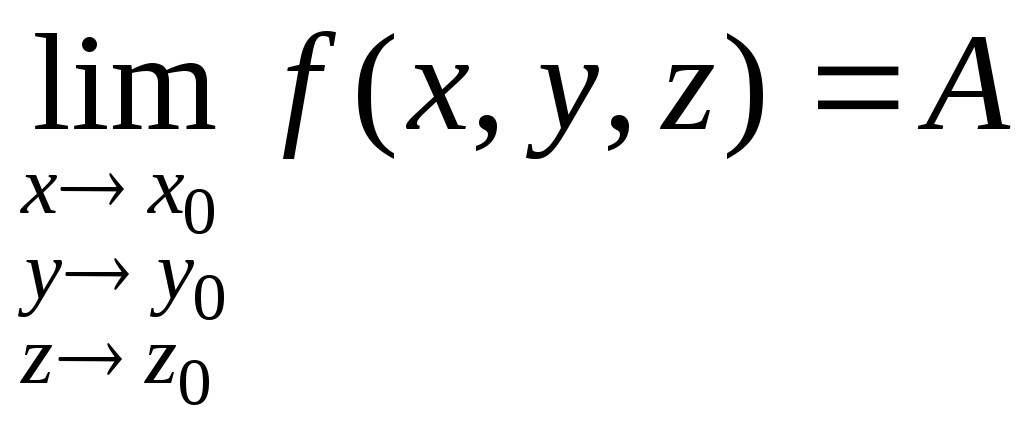 . 7
. 7 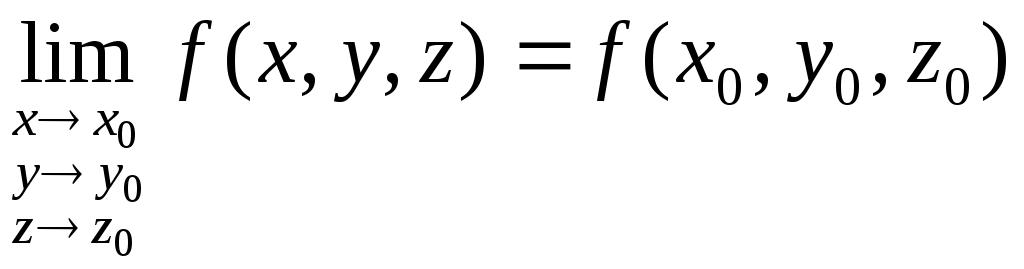 . 9
. 9 

