Предел и непрерывность функции нескольких переменных. Частные производные. 51. Предел и непрерывность функции нескольких переменных. Частны. Функции нескольких переменных с примерами решения Функции нескольких переменных
 Скачать 397.26 Kb.
|
|
Функции нескольких переменных с примерами решения Функции нескольких переменных: Многим явлениям, в том числе экономическим, присуща многофакторная зависимость. Исследование таких зависимостей потребовало совершенствования математического аппарата, в частности введения понятия функции нескольких переменных. Определение. Пусть имеется Например, формула  задает объем цилиндра как функцию двух переменных: (радиуса основания) и (высоты).Переменные  называются независимыми переменными или аргументами, — зависимой переменной, а символ означает закон соответствия. Множество называется областью определения функции. Очевидно, это подмножество -мерного пространства.Пример: Найти область определения функции: 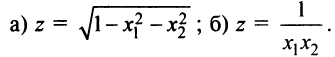 Решение: а) Область определения задается условием:  или  т.е. представляет собой единичный круг с центром в начале координат.б) Имеем  т.е. область определения — это плоскость  за исключением координатных прямых  и  Рассмотрим некоторые примеры функций нескольких переменных. 1. Функция  где  — постоянные числа, называется линейной. Ее можно рассматривать как сумму линейных функций от переменных  2. Функция  , — постоянные числа) называется квадратической. В отличие от предыдущего примера квадратическая функция не является сепарабельной, т.е. не раскладывается в сумму функций одной переменной.3. В § 5.6 была определена функция полезности — одно из базовых понятий экономической теории. Многомерный ее аналог — это функция  выражающая полезность от п приобретенных товаров. Чаще всего встречаются следующие ее виды: — логарифмическая функция; Здесь  Такая функция называется функцией постоянной эластичности. Также на случай переменных обобщается понятие производственной функции (см. § 5.6), выражающей результат производственной деятельности от обусловивших его факторов  Приведем здесь наиболее часто встречающиеся виды производственных функций ( —величина общественного продукта, — затраты труда, — объем производственных фондов), полагая для простоты  а) функция Кобба—Дугласа  б) функция с постоянной эластичностью замещения:  В настоящей главе мы будем вести изложение в основном для функций двух переменных  при этом практически все понятия и теоремы, сформулированные для  легко переносятся и на случай  Однако рассмотрение случая двух переменных позволяет использовать наглядную геометрическую иллюстрацию основных понятий настоящей главы.Функцию двух переменных будем обозначать в дальнейшем  Тогда ее область определения есть подмножество координатной плоскости  Окрестностью точки  называется круг, содержащий точку  (см. рис. 15.1). Очевидно, круг на плоскости есть двумерный аналог интервала на прямой. При изучении функций нескольких переменных во многом используется уже разработанный в предыдущих главах математический аппарат. А именно: любой функции  можно поставить в соответствие пару функций одной переменной: при фиксированном значении  функцию и при фиксированном значении  функцию  Следует иметь в виду, что хотя функции  и имеют одно и то же «происхождение», вид их может существенно различаться. Рассмотрим, например, функцию  , выражающую величину вклада через лет при ставке  . Очевидно, что это функция степенная по и показательная по .Графиком функции двух переменных называется множество точек трехмерного пространства  аппликата которых связана с абсциссой и ординатой у функционального соотношения .График функции двух переменных , вообще говоря, представляет собой некоторую поверхность в трехмерном пространстве.Для построения графика функции полезно рассматривать функции одной переменной  представляющие сечения графика плоскостями, параллельными координатным плоскостям  т.е. плоскостями Пример: Построить график функции  Решение: Сечения поверхности 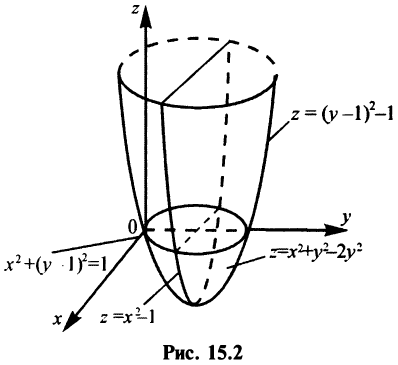  плоскостями, параллельными координатным плоскостям  представляют параболы (например, при    и т.д.). В сечении поверхности координатной плоскостью  получается окружность  График функции представляет поверхность, называемую параболоидом (см. рис. 15.2). ► Как видно, график функции двух переменных — значительно более сложный объект, чем график функции одной переменной. Как правило, построение поверхности оказывается довольно трудной задачей. В то же время поверхность в пространстве обладает гораздо меньшей наглядностью, чем линия на плоскости. Поэтому в случае двух переменных для изучения поведения функции желательно использовать другие, более наглядные инструменты. Важнейшим из них являются линии уровня. Определение._Линией_уровня'>Определение. Линией уровня функции двух переменных 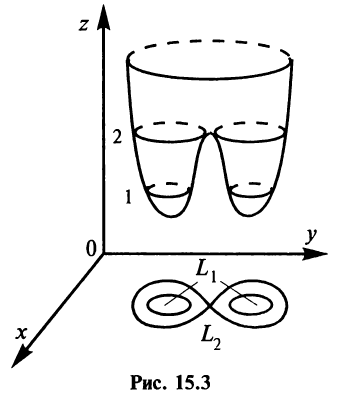называется множество точек на плоскости, таких, что во всех этих точках значение функции одно и то же и равно . Число в этом случае называется уровнем. На рис. 15.3 изображены линии уровня, соответствующие значениям  Как видно, линия уровня состоит из двух непересекающихся кривых. Линия — самопересекающаяся кривая.Многие примеры линий уровня хорошо известны и привычны. Например, параллели и меридианы на глобусе — это линии уровня функций широты и долготы. Синоптики публикуют карты с изображением изотерм — линий уровня температуры. В § 15.10 мы рассмотрим примеры использования линий уровня функций нескольких переменных в экономическом анализе. Построение линий уровня оказывается существенно более легкой задачей, чем построение графиков самих функций. Пример: Построить линии уровня функции  Решение: Линия уровня 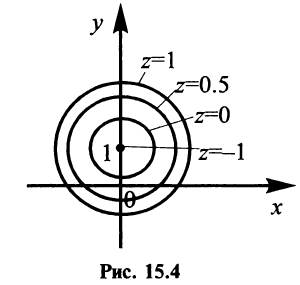 — это кривая на плоскости  задаваемая уравнением  Это уравнение окружности с центром в точке  и радиусом  (рис. 15.4). Точка  —это вырожденная линия уровня, соответствующая минимальному значению функции достигаемому в точке . Линии уровня — концентрические окружности, радиус которых увеличивается с ростом  ,причем расстояния между линиями с одинаковым шагом уровня уменьшаются по мере удаления от центра. Линии уровня позволяют представить график данной функции, который бы ранее построен на рис. 15.2. ►Предел и непрерывность Большая часть понятий математического анализа, определенных ранее для функций одной переменной, может быть перенесена на случай двух переменных. Определение. Число называется пределом функции   (или  ), если для любого даже сколь угодно малого положительного числа  найдется положительное число  (зависящее от  ), такое, что для всех точек  , отстоящих от точки  на расстояние меньшее, чем (т.е. при  ), выполняется неравенство  Обозначается предел так:  Пример: Найти предел 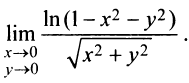 Решение: Обозначим 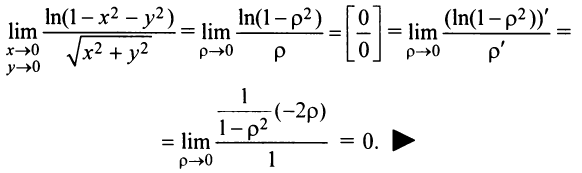 Условие  равносильно тому, что  Запишем предел в виде  Как правило, вычисление пределов функций двух переменных оказывается существенно более трудной задачей по сравнению со случаем одной переменной. Причина заключается в том, что на прямой существуют всего два направления, по которым аргумент может стремиться к предельной точке — а именно, справа и слева. На плоскости же таких направлений — бесконечное множество, и пределы функции по разным направлениям могут не совпадать. Пример: Доказать, что 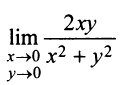 не существует.Решение: Будем приближаться к точке  по прямым  Если  Получили, что значение предела зависит от углового коэффициента прямой. Но так как предел функции не должен зависеть от способа приближения точки  к точке  (например, по прямой  ), то рассматриваемый предел не существует. ►Определение. Функция  называется непрерывной в точке  если она: 1) определена в точке  2) имеет конечный предел при  3) этот предел равен значению функции в точке   Геометрический смысл непрерывности очевиден: график в точке  представляет собой сплошную, нерасслаивающуюся поверхность.Частные производные Дадим аргументу приращение , аргументу — приращение Тогда функция получит наращенное значение  Величина  называется полным приращением функции в точке  Если задать только приращение аргумента или только приращение аргумента , то полученные приращения функции соответственно  называются частными.Полное приращение функции, вообще говоря, не равно сумме частных, т.е.  Пример: Найти частные и полное приращения функции  Решение:    Получили, что  Определение. Частной производной функции нескольких переменных по одной из этих переменных называется предел отношения соответствующего частного приращения функции к приращению рассматриваемой независимой переменной при стремлении последнего к нулю (если этот предел существует). Обозначается частная производная так: 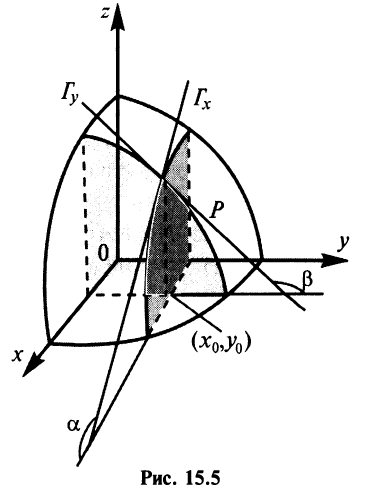 или  или    Таким образом, для функции 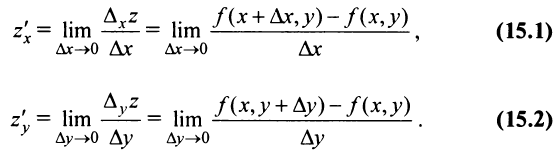 по определению Геометрический смысл частных производных функции в точке  показан на рис. 15.5.Пусть график функции представляет некоторую поверхность Тогда при  мы получаем кривую — сечение этой поверхности соответствующей плоскостью.В этом случае производная выражает угловой коэффициент касательной к кривой , в заданной точке  т.е.  где угол наклона касательной к оси Аналогично Из определения частных производных (15.1), (15.2) следует, что для нахождения производной  надо считать постоянной переменную , а для нахождения  — переменную . При этом сохраняются известные из гл. 7 правила дифференцирования.Пример: Найти частные производные функций:  Решение: а) Чтобы найти частную производную по , считаем постоянной величиной. Таким образом,  Аналогично, дифференцируя по , считаем постоянной величиной, т.е.  б) При фиксированном у имеем степенную функцию от . Таким образом,  При фиксированном функция является показательной относительно  Пример: Поток пассажиров выражается функцией  , где — число жителей, — расстояние между городами. Найти частные производные и пояснить их смысл.Решение: Производная  показывает, что при одном и том же расстоянии между городами увеличение потока пассажиров пропорционально удвоенному числу жителей. Производная  показывает, что при одной и той же численности жителей увеличение потока пассажиров обратно пропорционально квадрату расстояния между городами. ►Дифференциал функции Дифференциал функции  определялся как главная, линейная относительно , часть приращения функции, равная произведению  Обобщая определение дифференциала функции на случай двух независимых переменных, приходим к следующему определению. Определение. Дифференциалом функции называется сумма произведений частных производных этой функции на приращения соответствующих независимых переменных, т.е.  Учитывая, что для функций  согласно (15.3)  формулу дифференциала (15.3) можно записать в виде или  Определение. Функция  называется дифференцируемой в точке  , если ее полное приращение может быть представлено в виде где — дифференциал функции,  — бесконечно малые при  Таким образом, дифференциал функции двух переменных, как и в случае одной переменной, представляет главную, линейную относительно приращений  часть полного приращения функции.Можно показать, что если полное приращение функции представляет геометрически приращение аппликаты поверхности 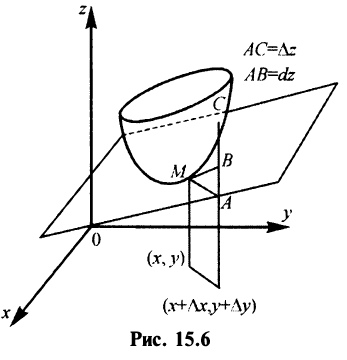 , то дифференциал функции есть приращение аппликаты касательной плоскости к поверхности в данной точке, когда переменные  получают приращения  (см. рис. 15.6). Следует отметить, что для функции одной переменной существование конечной производной  и представление приращения функции в виде (9.1), т.е.  , являются равнозначными утверждениями, и любое из них могло быть взято за определение дифференцируемости функции.Для функции нескольких переменных дело обстоит иначе: существование частных производных является лишь необходимым, но недостаточным условием дифференцируемости функции. Следующая теорема выражает достаточное условие дифференцируемости функции двух переменных. Теорема. Если частные производные функции  существуют в окрестности точки  и непрерывны в самой точке , то функция  дифференцируема в этой точке. |