1 Ошибки измерений 4 Цели математической обработки результатов эксперимента 4
 Скачать 0.72 Mb. Скачать 0.72 Mb.
|
|
Содержание 1 Ошибки измерений 4 Цели математической обработки результатов эксперимента 4 Виды измерений и причины ошибок 5 Типы ошибок измерения 6 Свойства случайных ошибок 7 Наиболее вероятное значение измеряемой величины 9 2 Методы обработки экспериментальных данных 10 Сглаживание табличных данных 10 Основные правила составления таблиц 11 Сглаживание табличных данных и графиков 13 Способ разностного сглаживания 14 Методы интерполяции и экстраполяции 16 Установление параметров и видов законов распределения случайных величин 20 Определение параметров эмпирических формул 22 Порядок действий при использовании метода средних 22 Список использованной литературы 26 Введение При исследовании технических систем могут использоваться теоретические и эмпирические методы познания. Каждое из этих направлений обладает относительной самостоятельностью, имеет свои достоинства и недостатки. В общем случае, теоретические методы в виде математических моделей позволяют описывать и объяснять взаимосвязи элементов изучаемой системы или объекта в относительно широких диапазонах изменения переменных величин. Однако при построении теоретических моделей неизбежно введение каких‒либо ограничений, допущений, гипотез и т.п. Поэтому возникает задача оценки достоверности (адекватности) полученной модели реальному процессу или объекту. Для этого проводится экспериментальная проверка разработанных теоретических моделей. Практика является решающей основой научного познания. В ряде случаев именно результаты экспериментальных исследований дают толчок к теоретическому обобщению изучаемого явления. Экспериментальное исследование дает более точное соответствие между изучаемыми параметрами. Но не следует и преувеличивать результаты экспериментальных исследований, которые справедливы только в пределах условий проведенного эксперимента. Таким образом, теоретические и экспериментальные исследования дополняют друг друга и являются составными элементами процесса познания окружающего нас мира. Как правило, результаты экспериментальных исследований нуждаются в определенной математической обработке. В настоящее время процедура обработки экспериментальных данных достаточно хорошо формализована и исследователю необходимо только ее правильно использовать. Круг вопросов, решаемых при обработке результатов эксперимента, не так уж велик. Это ‒ вопросы подбора эмпирических формул и оценка их параметров, вопросы оценки истинных значений измеряемых величин и точности измерений, вопросы исследования корреляционных зависимостей и некоторые другие. 1 Ошибки измерений Основой всего естествознания является наблюдение и эксперимент. Наблюдение ‒ это систематическое, целенаправленное восприятие того или иного объекта или явления без воздействия на изучаемый объект или явление. Наблюдение позволяет получить первоначальную информацию по изучаемому объекту или явлению. Эксперимент ‒ метод изучения объекта, когда исследователь активно и целенаправленно воздействует на него путем создания искусственных условий или использует естественные условия, необходимые для выявления соответствующих свойств. Достоинствами эксперимента по сравнению с наблюдением реального явления или объекта является: 1. Возможность изучения в «чистом виде», без влияния побочных факторов, затемняющих основной процесс; 2. В экспериментальных условиях можно получить результат более быстро и точно; 3. При эксперименте можно проводить испытания столько раз, сколько это необходимо. Результат эксперимента или измерения всегда содержит некоторую погрешность. Если погрешность мала, то ею можно пренебречь. Однако при этом неизбежно возникают два вопроса: во‒первых, что понимать под малой погрешностью, и, во‒вторых, как оценить величину погрешности. То есть, и результаты эксперимента нуждаются в определенном теоретическом осмыслении. 1.1 Цели математической обработки результатов эксперимента Целью любого эксперимента является определение качественной и количественной связи между исследуемыми параметрами, либо оценка численного значения какого‒либо параметра. В некоторых случаях вид зависимости между переменными величинами известен по результатам теоретических исследований. Как правило, формулы, выражающие эти зависимости, содержат некоторые постоянные, значения которых и необходимо определить из опыта. Другим типом задачи является определение неизвестной функциональной связи между переменными величинами на основе данных эксперимента. Такие зависимости называют эмпирическими. Однозначно определить неизвестную функциональную зависимость между переменными невозможно даже в том случае, если бы результаты эксперимента не имели ошибок. Тем более не следует этого ожидать, имея результаты эксперимента, содержащие различные ошибки измерения. Поэтому следует четко понимать, что целью математической обработки результатов эксперимента является не нахождение истинного характера зависимости между переменными или абсолютной величины какой‒либо константы, а представление результатов наблюдений в виде наиболее простой формулы с оценкой возможной погрешности ее использования. 1.2 Виды измерений и причины ошибок Под измерением понимают сравнение измеряемой величины с другой величиной, принятой за единицу измерения. Различают два типа измерений: прямые и косвенные. При прямом измерении измеряемая величина сравнивается непосредственно со своей единицей меры. Например, измерение микрометром линейного размера, промежутка времени при помощи часовых механизмов, температуры ‒ термометром, силы тока ‒ амперметром. Значение измеряемой величины отсчитывается при этом по соответствующей шкале прибора. При косвенном измерении измеряемая величина определяется (вычисляется) по результатам измерений других величин, которые связаны с измеряемой величиной определенной функциональной зависимостью. Например, измерение скорости по пройденному пути и затраченному времени, измерение плотности тела по измерению массы и объема, температуры при резании по электродвижущей силе, величины силы ‒ по упругим деформациям и т.п. При измерении любой физической величины производят проверку и установку соответствующего прибора, наблюдение их показаний и отсчет. При этом никогда истинного значения измеряемой величины не получить. Это объясняется тем, что измерительные средства основаны на определенном методе измерения, точность которого конечна. При изготовлении прибора задается класс точности. Его погрешность определяется точностью делений шкалы прибора. Если шкала линейки нанесена через 1 мм, то точность отсчета Кроме приборной погрешности на результат измерения влияет еще ряд объективных и субъективных причин, обуславливающих появление ошибки измерения ‒ разности между результатом измерения и истинным значением измеряемой величины. Ошибка измерения обычно неизвестна, как неизвестно и истинное значение измеряемой величины. Исключение составляют измерения известных величин при определении точности измерительных приборов или их тарировке. Поэтому одной из важнейших задач математической обработки результатов эксперимента и является оценка истинного значения измеряемой величины по данным эксперимента с возможно меньшей ошибкой. 1.3 Типы ошибок измерения Кроме приборной погрешности измерения (определяемой методом измерения) существуют другие, которые можно разделить на три типа: Систематические погрешности обуславливаются постоянно действующими факторами. Например, смещение начальной точки отсчета, влияние нагревания тел на их удлинение, износ режущего лезвия и т.п. Систематические ошибки выявляют при соответствующей тарировке приборов и потому они могут быть учтены при обработке результатов измерений. Случайные ошибки содержат в своей основе много различных причин, каждая из которых не проявляет себя отчетливо. Случайную ошибку можно рассматривать как суммарный эффект действия многих факторов. Поэтому случайные ошибки при многократных измерениях получаются различными как по величине, так и по знаку. Их невозможно учесть, как систематические, но можно учесть их влияние на оценку истинного значения измеряемой величины. Анализ случайных ошибок является важнейшим разделом математической обработки экспериментальных данных. Грубые ошибки (промахи) появляются вследствие неправильного отсчета по шкале, неправильной записи, неверной установки условий эксперимента и т.п. Они легко выявляются при повторном проведении опытов. В дальнейшем будем считать, что систематические и грубые ошибки из результатов эксперимента исключены. 1.4 Свойства случайных ошибок Случайные ошибки бывают как положительные, так и отрицательные разной величины, не превосходящей определенного предела. Если обозначить через Х истинное значение измеряемой величины, а результат первого измерения ‒ à1, то разность Х ‒ à1 = х1 или à1 ‒ Х = х1 называют истинной абсолютной ошибкой одного измерения. Одновременно она является случайной (при исключении систематических и грубых ошибок). Если измерения провести многократно в одних и тех же условиях, то результаты отдельных измерений одинаково надежны. Такую совокупность измерений а1, а2 ...аn называют равноточными измерениями. Если проанализировать достаточно большую серию равноточных измерений и соответствующих случайных ошибок измерений, то можно выделить четыре свойства случайных ошибок: Число положительных ошибок почти равно числу отрицательных; Мелкие ошибки встречаются чаще, чем крупные; Величина наиболее крупных ошибок не превосходит некоторого определенного предела, зависящего от точности измерения. Самую большую ошибку в ряду равноточных измерений называют предельной ошибкой; Частные от деления алгебраической суммы всех случайных ошибок на их общее близко к нулю, т.е. 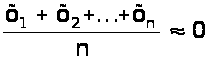 . .На основе указанных свойств при учете некоторых допущений математически достаточно строго выводится закон распределения ошибок, описываемый следующей функцией: 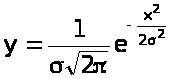 , ,где s ‒ дисперсия измерений (см. ниже); е ‒ основание натуральных логарифмов; х ‒ истинная абсолютная ошибка измерений. Закон распределения случайных ошибок является основным в математической теории погрешностей. Иначе его называют нормальным законом распределения. Особое значение в пользу широкого использования закона Гаусса имеет следующее обстоятельство: если суммарная ошибка измерения появляется в результате совместного действия ряда причин, каждая их которых вносит малую долю в общую ошибку (т.е. нет доминирующих причин), то по какому бы закону не были распределены ошибки, вызываемые каждой из причин, результат их совместного действия приведет к нормальному распределению ошибок. Эта закономерность является следствием так называемой центральной предельной теоремы Ляпунова и хорошо соотносится с введенным понятием случайной ошибки. Наряду с нормальным законом распределения ошибок могут встречаться и другие. 1.5 Наиболее вероятное значение измеряемой величины Допустим, что для определения истинного значения Х измеряемой величины было сделано n равноточных измерений с результатами а1, а2 ...аn. Естественно, что ряд этих чисел будет больше Х, другие меньше Х и неясно, какое из этих чисел ближе всего подходит к Х. Представим результаты измерений в виде очевидных равенств: а1 = Х ‒ Dх1; а2 = Х ‒ Dх2; ... ; аn = Х ‒ Dхn. Естественно, что истинные абсолютные ошибки Dхi могут принимать как положительные, так и отрицательные значения. Суммируя левые и правые стороны равенств, получим: 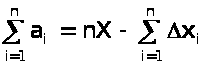 . .Поделим обе части равенства на число измерений n и получим 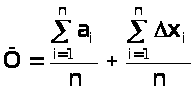 . .Величина 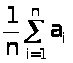 является среднеарифметическим величины Х. Если число n достаточно велико, то согласно четвертому свойству случайных ошибок является среднеарифметическим величины Х. Если число n достаточно велико, то согласно четвертому свойству случайных ошибок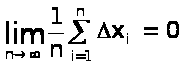 . .Это же видно и по кривой Гаусса, где всякой положительной погрешности соответствует равная ей отрицательная. Следует еще раз подчеркнуть, что среднеарифметическое значение, принимаемое за истинное значение измеряемой величины, является наиболее вероятным значением. Среди значений аi могут оказаться значения, которые в действительности ближе к истинному значению. Отклонение Dх вероятнейшего значения, а от его истинного значения Х называют истинной абсолютной ошибкой. 2 Методы обработки экспериментальных данных 2.1 Сглаживание табличных данных Экспериментальные исследования, проводимые как в натуре, так и на моделях, должны быть предварительно тщательно продуманы не только в отношении порядка их проведения, но и в отношении выбора способов обработки результатов наблюдения. Наблюдения обобщают не только по окончании опытов, но и в ходе проведения. Внимательный и добросовестный исследователь всегда стремится еще в процессе опытов установить необходимые закономерности, возможные отклонения и их причины, новые факторы, связи, взаимодействия. Для обобщения используют все материалы наблюдений: таблицы записей, осциллограммы, записи на магнитных носителях, фотоснимки и т.д. Не следует забывать и мелких заметок, так как иногда подмеченное во время опыта явление, кажущееся случайным, может объяснить причины и развитие явлений. Сопоставляя все материалы, исследователь ищет раскрытие связей взаимодействия, функциональных зависимостей факторов. Установив их, он выделяет главные связи, зависимости, взаимодействия и устанавливает общие закономерности явлений. При обработке опытных данных надо стремиться как можно более разносторонне представить различные связи и отношения, сопоставить значения отклонений, скорости изменения величин и соответствующих ускорений, максимумов и минимумов, сравнивать различные величины, расположенные в порядке увеличения или уменьшения их значений и применять другие приемы. Функциональные связи легче найти, если данные опытов представить таблицами или графиками. В таблице вначале выделяют по физическому смыслу аргумент (независимую переменную), затем функцию (зависимую переменную). Желательна следующая форма таблицы: номер и краткое, точное название; в первом столбце располагают значения аргумента, а в остальных ‒ значения функций. Иногда целесообразно несколько столбцов объединять в один раздел с общей заголовочной частью и подзаголовками в каждом столбце. 2.2 Основные правила составления таблиц 1. Аргумент располагают строго логично основному, существенному признаку (например, по величине, в возрастающем или убывающем порядке). 2. Все столбцы должны иметь краткие, ясные заголовки с указанием размерности помещаемых величин. 3. При заполнении таблицы следует помнить, что, если данных нет, надо ставить тире, а не ноль – это определенное значение аргумента или функции. Запятые, отделяющие целую часть от дробной, в каждой графе следует располагать одну под другой (в линию). 4. Проще всего размещать в таблице результаты опытов с одной повторностью, так как при этом не требуется каких‒либо вычислений. Пусть, например, при измерениях частоты вращения коленчатого вала двигателя в лабораторный журнал записаны данные в следующем виде (табл. 1). В таком виде данные опытов трудно считать и закономерности остаются неясными. Выделим аргумент по физическому смыслу. Понятно, что температура воды в радиаторе и масла в картере не могут быть аргументом. Т а б л и ц а 1 ‒ Данные опытов
Сопротивление трения в опытах не регулировали и интервалы по нему между данными различных опытов неравномерны. Из этих соображений считаем аргументом частоту вращения вала двигателя в минуту и располагаем аргумент в возрастающем порядке. За аргументом располагаем, как наиболее существенную функцию, данные о сопротивлении трения (табл. 2). Т а б л и ц а 2 ‒ Данные опытов
Как видно из таблицы функциональные связи стали яснее. Общей закономерностью является увеличение сопротивление трения и понижения температуры воды в радиаторе; температура же масла в функции частоты вращения вала падает медленно. Сложнее составить таблицу при большой повторности измерений. |
