микроэкономика практическое задание. 1. Основы микроэкономики

• Название: 1. Основы микроэкономики
• Дата: 26.10.2022
• Размер: 296.49 Kb.
• Имя файла: микроэкономика практическое задание.docx
• Тип: Задача; #755170
• страница: 2 из 3

Тема 2. Поведение потребителя: бюджетные ограничения и выбор

Задача

Известно, что для потребительского набора функция полезности потребителя задана уравнением . Общий доход, которым располагает потребитель, составляет . Цена товара – ден. ед., цена товара – ден. ед. Предположим, что цена товара снижается до уровня .

Осуществите следующие действия:

- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;

- определите эффект замены (по Хиксу);

- определите эффект дохода (по Хиксу);

- определите общий эффект (по Хиксу);

- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).
Бланк выполнения практического задания 3

Задача

Известно, что для потребительского набора функция полезности потребителя задана уравнением . Общий доход m, которым располагает потребитель, составляет 240 ден. ед. Цена товара – ден. ед., цена товара – ден. ед. Предположим, что цена товара снижается до уровня .

Осуществите следующие действия:

- выпишите уравнение бюджетной линии и постройте график бюджетного ограничения;

- определите эффект замены (по Хиксу);

- определите эффект дохода (по Хиксу);

- определите общий эффект (по Хиксу);

- охарактеризуйте данный товар (нормальный, инфериорный, товар Гиффена).

Решение

1. 
   Бюджетное ограничение по заданным значениям и принимает вид: .
   

Функция полезности потребителя представляет собой функцию Кобба-Дугласа (Функция вида  ).

2. 
   Метод Хикса заключается в том, что реальный доход измеряется полезностью благ, на которые расходуется денежный доход.
   

Графическое представление оптимальной точки – это точка касания бюджетного ограничения потребителя и кривой безразличия. Исходя из этого, в точке оптимума угол наклона кривой безразличия ( 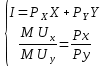) равен углу наклона бюджетного ограничения ( ).



Решая данную систему для функции вида Кобба-Дугласа ( ), находим выражения для оптимального количества товаров Х и У.

 

Полученные формулы справедливы для любой функции Кобба-Дугласа и получили название «метода долей дохода». Воспользуемся данным методом для расчета первоначальной точки оптимума потребителя, в которой он находился до изменения цены товара Y: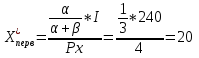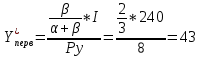





Таким образом, первоначально потребитель потреблял 20 ед. товара Х и 43 ед. товара У; при этом он достигал уровня полезности U1=2*x²*y=2*20²*20=16000 ютилей

Оптимальный выбор потребителя представлен на рисунке 3.1.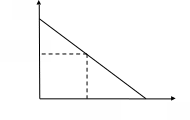




Рис. 3.1. Потребительский выбор


Аналогично можно рассчитать объемы товаров Х и У после изменения цены на товар У, то есть конечную оптимальную точку.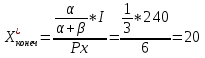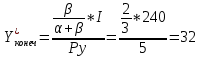





Следовательно, после снижения цены товара У, потребитель увеличил объем потребления этого товара на 32 единиц.

Таким образом, общий эффект от снижения цены товара У равен +12 ед. (ΔY_общий=Y_{конечное} – Y_{начальное} = 32-20).

3. 
   Эффект замены (по Хиксу) отражает на сколько бы изменился объем потребления блага при изменении его цены в условиях сохранения потребителем прежнего (первоначального) уровня полезности.
   

Необходимо построить вспомогательное бюджетное ограничение, параллельное новому бюджетному ограничению (с новыми ценами), которое бы являлось касательным к первоначальной кривой безразличия.

Для расчета вспомогательной точки (координаты 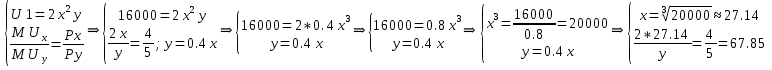и ) необходимо решить систему из двух уравнений:

1)  , которое означает, что в ходе эффекта замены потребитель остается на первоначальном уровне полезности (эта предпосылка основана на том, что мы рассчитываем эффекты по методу Хикса).

2)   соответствует условию оптимума, то есть условию касания построенного нами вспомогательного бюджетного ограничения (БО₃), параллельного новому бюджетному ограничению (БО₂), первоначальной кривой безразличия (КБ₁). То есть угол наклона нового бюджетного ограничения (он равен соотношению новых цен Рх/Ру₂) в точке оптимума должен быть равен углу наклона кривой безразличия (угол наклона кривой безразличия в точке равен отношению предельных полезностей MUx/MUy).



График потребительского выбора представлен на рисунке 3.2.



… …………..

Эффект замены при снижении цены товара показывает на сколько бы изменился объем потребления блага при изменении его цены в условиях сохранения потребителем прежнего (первоначального) уровня полезности.

В данной задаче: Эффект ЗАМЕНЫ: при снижении цены товара У, объем потребления товара У (при сохранении потребителем первоначального уровня полезности) увеличился на 1,7 ед. (ΔY_замены=Y_{промежуточное} – Y_{начальное} =68-20=48

4. 
   Эффект дохода (по Хиксу) показывает на сколько изменится объем потребления данного блага за счет того, что потребитель начинает чувствовать себя богаче (рост реального дохода потребителя при снижении цены на товар) или беднее (снижение реального дохода при росте цены).
   

В данной задаче: Эффект ДОХОДА: при снижении цены товара У, что эквивалентно росту реального дохода потребителя, объем потребления товара У уменьшился на 42 ед. (ΔY_дохода=Y_{конечное} – Y_{промежуточное} =32-68), то есть обратная зависимость между изменением реального дохода и объемом потребления, следовательно Y - товар инфериорный.

Вывод: товар У является нормальным (качественным товаром). Закон спроса (обратная зависимость между ценой товара и объемом потребления ) не нарушен (в данном случае, цена товара У снизилась, что в итоге привело к росту объема потребления данного товара на 60 единиц (то есть обратная зависимость).

Практическое задание 4
Тема 3. Поведение производителя и конкуренция

Задачи

1. 
   Технологическая норма замещения факторов и равна . Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора на единиц. Сколько дополнительных единиц фактора потребуется фирме?
   

Бланк выполнения практического задания 4

1. 
   Технологическая норма замещения факторов и равна . Предположим, что фирма готова произвести тот же самый объем выпуска, но сократить использование фактора на единиц. Сколько дополнительных единиц фактора потребуется фирме?
   

Решение

Условие оптимального использования ресурсов: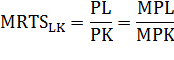



т.е. отношение цен на ресурсы равно отношению предельных продуктов этих ресурсов.

Изокванты показывают равные объемы выпуска при разных сочетаниях используемых ресурсов. Для производителя важно знать, как выбрать такое сочетание ресурсов, чтобы достичь максимального объема при минимальных издержках.

Точки А, Е, В лежат на одной и той же изокосте CC_t и, следовательно, затраты предприятия на ресурсы в этих точках составят одну и ту же сумму С. Но наиболее предпочтительной является комбинация Е, так как ^еи соответствует более высокий объем выпуска (Q₂ > Q₁). C другой стороны,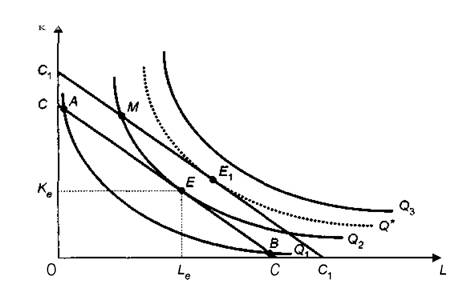



Рис. 4-1. Оптимум производителя
Комбинация M столь же технически эффективна, как и комбинация E (достигается тот же объем Q₂ при иной комбинации объемов KmL),- они лежат на той же изокванте.

Но при данных ценах ресурсов точка M экономически неэффективна (за ту же сумму C₁ можно получить больший объем Q*).

Если бюджет производителя возрастает, он получает возможность выходить на новые изокванты. Каждая точка касания показывает такую комбинацию факторов, которая соответствует минимуму затрат на производство данного объема продукции, обозначенного на изокванте. Соединив точки, получим линию роста фирмы, которая получила название изоклинали (рис. 4-2).

В нашем случае, наоборот, наблюдается снижение бюджета производителя, поэтому должен вырасти ресурс L на то же количество на которое уменьшился продукт K.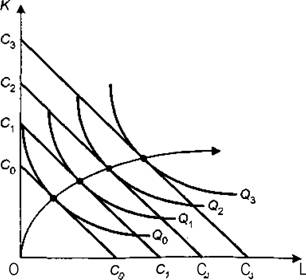



Рис. 4-2. Линия роста фирмы (изоклиналь)
Графическое решение представлено на рисунке 4-2.

Вывод: в результате проведенных расчетов при сокращении использования фактора на единиц фирме потребуется 2 дополнительная единица фактора .
Практическое задание 5
Тема 4. Рыночные структуры и стратегия поведения

Задачи

1. Предположим, что на рынке действуют две фирмы, функции общих издержек заданы уравнениями: и . Рыночный спрос описывается функцией:

,

где .

Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:

- фирмы конкурируют по Курно;

- фирмы конкурируют по Бертрану;

- фирмы конкурируют по сценарию Штакельберга.

Изобразите решение на графике.

3. График предельных издержек фирмы-монополиста задан условием . Функция предельного дохода принимает вид: . Определите эластичность рыночного спроса при оптимальном выпуске фирмы-монополиста.

Рекомендации по выполнению практического задания 5

Изучив материалы по теме «Рыночные структуры и стратегия поведения», выполните расчеты в бланке выполнения практического задания 5 и покажите графическое решение.
Бланк выполнения практического задания 5

Задачи

1. Предположим, что на рынке действуют две фирмы, функции общих издержек заданы уравнениями: и . Рыночный спрос описывается функцией:

,

где .

Определите объем продаж, который будет у каждой фирмы, и цену, которая установится на рынке, если:

- фирмы конкурируют по Курно;

- фирмы конкурируют по Бертрану;

- фирмы конкурируют по сценарию Штакельберга.

Изобразите решение на графике.

Решение

1. 
   Стратегия по Курно предполагает, что количественную конкуренцию компаний, которые принимают решение о выпуске самостоятельно
   

Решение задачи по Курно:

Подставим общий выпуск двух фирм

Q = q₁ + q₂

в формулу отраслевого спроса, получим:

Р=1000-1/4( )

Выводим функции совокупного дохода каждой из стран:

TR=P*Q

TR₁=1000Q₁-1/4Q₁²-1/4Q₁Q₂

TR₂=1000Q₂-1/4Q₂²- 1/4Q₁Q₂

Находим предельный доход:

MR=TR’

MR₁=1000-0,5Q₁- 0,25Q₂

MR₂=1000-0,5Q₂- 0,25Q₁

Из условия максимизации прибыли:

MC=MR

МС=TC’

MC₁=2Q₁

1000-0,5Q₁- 0,25Q₂=2Q₁

1000-2,5Q₁- 0,25Q₂=0

MC₂=0,5Q₂

1000-0,5Q₂- 0,25Q₁=0,5Q₂

1000-Q₂ -0,25Q₁=0

Находим кривые реакции:

- из первого уравнения кривая реакции первой фирмы:

Q₁=400-0,1Q₂

- из второго уравнения кривая реакции второй фирмы:

Q₂=1000-0,25Q₁

Решаем систему уравнений кривых реакции относительно Q₁ и находим равновесные объемы:

Q₁=400-0,1(1000-0,25 Q₁)

Q₁=308 ед.

Q₂=923 ед.

Q₁+Q₂=308+923=1231 ед.

Р=1000-0,25*1231=692 д.е.

Равновесная цена составит 692 д.е., а объем продажи фирмы 1 – 308 ед., а фирмы 2 – 923 ед.

Отраслевой выпуск составит 1231 ед.

Графическое решение представлено на рисунке 5.1.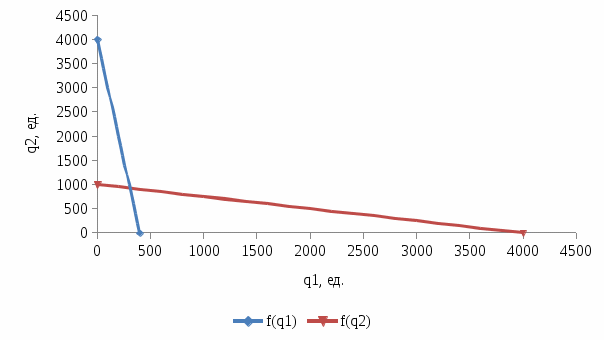



Рисунок 5.1 Равновесие по Курно

2. 
   Стратегия по Бертрану предполагает, что каждая фирма максимизирует прибыль, ожидая, что другая фирма не изменит свою цену. Результатом модели Бертрана является устойчивое равновесие двух фирм. Дуополисты Бертрана исходят из предположения о независимости цен, устанавливаемых друг другом, от их собственных ценовых решений, то есть цена, назначенная соперником, является для дуополиста константой.
   

Ценовая война продолжается до тех пор, пока не будет выполняться равенство Р = АС = МС.

3. 
   В соответствии с данным условием решение задачи по Бертрану принимает вид:
   

MC₁=2Q₁

MC₂=0,5Q₂

Фирма с более высокими издержками (фирма 1) вынуждена будет уйти из отрасли.

МС=Р

1000-0,25Q=0,5Q

Q=1333 ед.

Р=1000-0,25*1333=667 д.е.

Равновесный объем составит 1333 ед. по цене 667 д.е.

Графическое решение представлено на рисунке 5.2.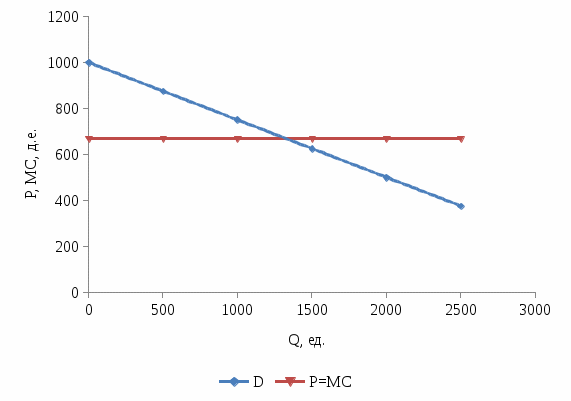



Рисунок 5.2 Рыночное равновесие по Бертрану

4. 
   Стратегия по Штакельбергу предполагает, что имеется иерархия игроков. Первым своё решение объявляет игрок I, после этого стратегиювыбирает игрок II.
   

Решение задачи по сценарию Штакельберга принимает вид:

Пусть фирма 2 выступает в роли лидера, а фирма 1 - в роли последователя.

Прибыль второй фирмы с учётом уравнения реакции фирмы 1 будет равна:

П₂=TR₂-TC₂=p*q₂-(20+0,25q₂²)= (1000-0,25( ))q₂-20-0,25q₂²=

=1000q₂-0,25q₁q₂-0,5q₂²=1000q₂-0,25*(400-0,1q₂)*q₂-0,5q₂²=

=900q₂-0,475q₂²

П₂’=900-0,95q₂=0

q₂=947 ед.

q₁=400-0,1*947=305 ед.

Равновесная цена составит Р=1000-0,25*(947+305)=687 д.е.

Графическое решение представлено на рисунке 5.3.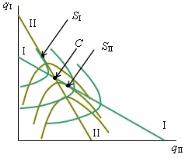



Рисунок 5.3 равновесие по Штакельбергу
Совместив карты изопрофит дуополистов, можно увидеть сочетания q_I,q_II, соответствующие отраслевому равновесию в моделях Курно и Штакельберга (рис. 5.3). Точка касания линии реакции последователя с наиболее низкой изопрофитой лидера представляет равновесие в модели Штакельберга (S_I или S_II).

Вывод: в результате пассивного поведения фирмы 1 ее объем продаж и соответственно прибыль снизятся.

2. График предельных издержек фирмы-монополиста задан условием . Функция предельного дохода принимает вид: . Определите эластичность рыночного спроса при оптимальном выпуске фирмы-монополиста.

Решение

1. 
   Определяем оптимальный выпуск фирмы-монополиста:
   

MR=MC

TR=60P-P²=P(60-P)=P*Q

Q=60-P

P=60-Q

TR=P*Q=60Q-Q²

MR=TR’=60-2Q

2Q=60-2Q

4Q=60

Q=15 ед.

Оптимальный выпуск монополиста составляет 15 ед.

2. 
   Выводим функцию спроса фирмы-монополиста:
   

Q=60-P

3. 
   Цена при оптимальном выпуске фирмы-монополиста составит 45 д.е. (60-15).
   
4. 
   Эластичность в точке :
   

Спрос эластичен.


Практическое задание 6