МАТЕМАТИЧЕСКИЕ МЕТОДЫ ТЕОРИИ СЕТЕЙ СВЯЗИ И ПЕРЕДАЧИ ДАННЫХ (ЦИКЛИЧЕСКИЕ КОДЫ) КОНТРОЛЬНАЯ РАБОТА. Математические методы теории сетей связи. 1 Основные алгебраические системы, используемые в теории кодирования
 Скачать 92.63 Kb. Скачать 92.63 Kb.
|
|
Математические методы теории сетей связи и передачи данных Содержание 1 Основные алгебраические системы, используемые в теории кодированияЗадание 1.5 Построить все возможные двоичные последовательности длины 5. Являются ли они группой по операции поразрядного сложения по mod 2? Доказать. Решение Количество двоичных последовательностей длины 5 равно 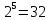 : :
Для того, чтобы данная последовательность являлась группой по операции поразрядного сложения по модулю два, необходимо выполнение групповых аксиом. Проверим их выполнение. Замкнутость. Поразрядное сложение по модулю 2 для суммы любых чисел из данной совокупности дает число из этой совокупности (других пятиразрядных двоичных чисел не существует). Ассоциативность и коммуникативность. Для операции сложения по модулю 2 результат сложения не зависит от очередности выбора суммируемых элементов из некоторой ассоциации, поэтому для нее ассоциативный и коммуникативный законы выполняются всегда. Наличие единичного элемента. Для данной совокупности единичным элементом будет являться последовательность 00000, так как при сложение ее с любой другой последовательностью не изменяет значения последней. Существование обратных элементов. Для любой последовательности сумма с точно такой же последовательностью даст в результате нулевую последовательность 00000, т. е. каждая двоичная последовательность является для себя обратной. Таким образом, все возможные двоичные последовательности длины 5 являются группой по операции поразрядного сложения по mod 2. 2 Кольца многочленов и поля ГалуаЗадание 2.4 Используя алгоритм Евклида, найти HOД (1573,308) и целые числа A и B, удовлетворяющие равенству HOД (1573,308) = 1573A+308B. Решение Воспользуемся алгоритмом Евклида:  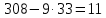  Т.е. НОД (1573,308) = 11 Представим полученный результат в виде 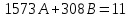 , для чего воспользуемся вычислениями НОД. , для чего воспользуемся вычислениями НОД. Выражение  подставляем во второй шаг алгоритма: подставляем во второй шаг алгоритма: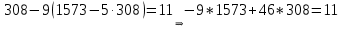 Теперь подставляем выражения для 33 и 11 в последний шаг алгоритма:  И получаем: 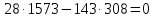 Дополняем найденные равенства двумя формальными равенствами в качестве исходных: 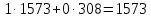 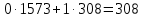 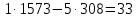  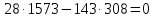 Определяем целую часть дроби  – общее выражение для – общее выражение для  , ,  в этом случае представимо как в этом случае представимо как  . .Для наглядности представим в виде таблицы:
3 Теорема Ферма и циклотомические классыЗадание 3.4 Определить все неприводимые сомножители следующих двучленов:  ; ; ; ;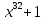 . .Решение А)  Поскольку  , то достаточно найти неприводимые сомножители , то достаточно найти неприводимые сомножители  . .Проверяем степени двойки. 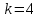  Имеем:  , значит все неприводимые многочлены 4-й степени будут делителями , значит все неприводимые многочлены 4-й степени будут делителями  и, следовательно, и, следовательно,  . Таких многочленов три: . Таких многочленов три:  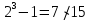  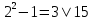 Имеем: 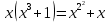 , значит все неприводимые многочлены 2-й степени будут делителями , значит все неприводимые многочлены 2-й степени будут делителями 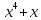 и, следовательно, и, следовательно,  . Такой многочлен только один: . Такой многочлен только один: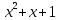  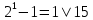 Имеем: 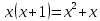 , значит единственный неприводимый многочлен 1-й степени делит , значит единственный неприводимый многочлен 1-й степени делит 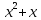 . Получили: . Получили: А, значит:  Б)  ; ;Т.к. 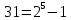 , а 5 – простое число, то делителями двучлена будут только , а 5 – простое число, то делителями двучлена будут только 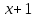 и все неприводимыми сомножителями 5-й степени: и все неприводимыми сомножителями 5-й степени: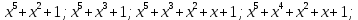 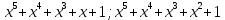 Т.е.:   В) 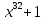 . .Т.к.  , то единственным неприводимым сомножителем будет являться неприводимый многочлен 1-й степени: , то единственным неприводимым сомножителем будет являться неприводимый многочлен 1-й степени: 4 Разложение |
| 0 | 000 |
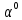 | 100 |
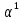 | 010 |
 | 001 |
 | 110 |
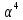 | 011 |
 | 111 |
 | 101 |
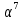 | 100 |
И получаем:
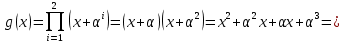
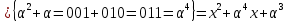
Т.е. порождающий многочлен для кода Рида-Соломона (7,5), способного исправлять до
 ошибки имеет вид
ошибки имеет вид 

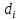
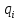
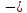
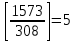
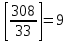

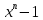 на
на 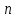 разложение
разложение  , где второй сомножитель неприводим.
, где второй сомножитель неприводим.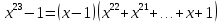


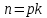 , где
, где 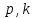 – простые числа, разложение имеет вид (последний сомножитель - неприводим):
– простые числа, разложение имеет вид (последний сомножитель - неприводим):
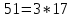 ,
,  , поэтому:
, поэтому: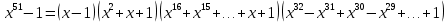
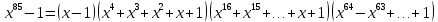
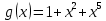 ;
; ;
;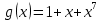 .
.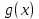 . По окончании деления в триггерах 1-4 делителя записывается остаток от деления. Если при этом хотя бы один из этих триггеров находится в единичном состоянии, то это означает, что в принятой кодовой комбинации имеется ошибка. На выходе схемы ИЛИ-НЕ формируется нулевой сигнал, который при замкнутом ключе К поступает на вход схемы И. На первый же вход схемы И поступает исходная кодовая комбинация. Под действием нулевого сигнала с выхода ИЛИ-НЕ схема И запирается и кодовая комбинация не поступает на выход схемы декодера.
. По окончании деления в триггерах 1-4 делителя записывается остаток от деления. Если при этом хотя бы один из этих триггеров находится в единичном состоянии, то это означает, что в принятой кодовой комбинации имеется ошибка. На выходе схемы ИЛИ-НЕ формируется нулевой сигнал, который при замкнутом ключе К поступает на вход схемы И. На первый же вход схемы И поступает исходная кодовая комбинация. Под действием нулевого сигнала с выхода ИЛИ-НЕ схема И запирается и кодовая комбинация не поступает на выход схемы декодера.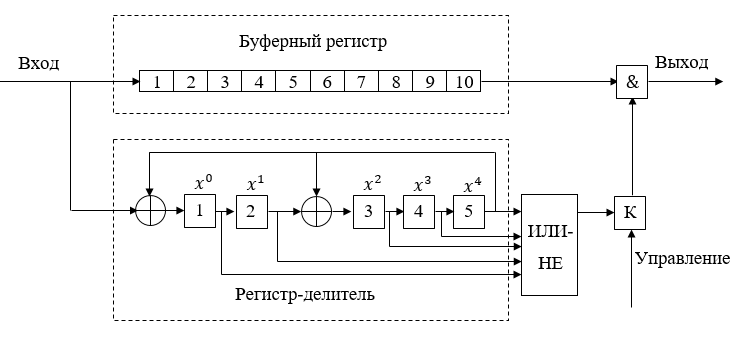

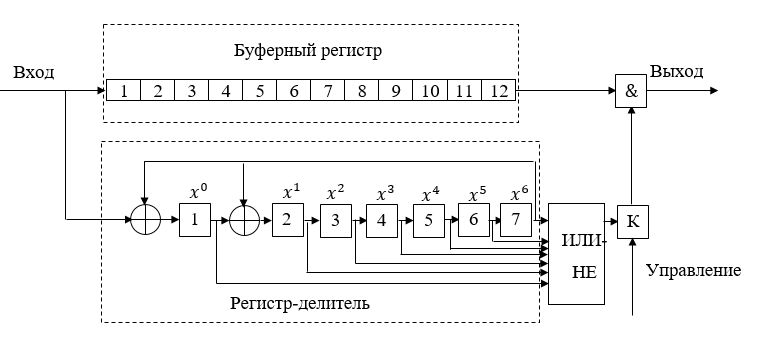

 .
.  :
: