Инжграф ответы. 1. Основные геометрические образы в курсе начертательной геометрии, аксиоматика курса. Инвариантные свойства параллельного проецирования
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
%D1%81%D1%81%D0%B5%D1%87%D0%B5%D0%BD%D0%B8%D0%B5&action=edit&redlink=1"рассечение 0%9F%D1%80%D0%B5%D0%B4%D0%BC%D0%B5%D1%82"предмета одной или несколькими 0%9F%D0%BB%D0%BE%D1%81%D0%BA%D0%BE%D1%81%D1%82%D1%8C_(%D0%B3%D0%B5%D0%BE%D0%BC%D0%B5%D1%82%D1%80%D0%B8%D1%8F)"плоскостями. На разрезе показываются также и те детали и их части, которые расположены за секущей плоскостью. 1. В зависимости от числа секущих плоскостей разрезы делятся на: Простой разрез — для формирования используется одна плоскость. Можно не обозначать, если изображение разреза находится на месте основного вида, на одном листе с главным видом, не отделено от главного вида другими изображениями. Сложный разрез — для формирования используются две и больше секущих плоскостей. Обозначается всегда. Ломаный разрез — для формирования используются две (бо́льшее количество используется редко) пересекающиеся плоскости. Ступенчатый разрез — для формирования используются две и более параллельные плоскости. 2. В зависимости от положения плоскости относительно горизонтальной плоскости проекции разрезы разделяются на: Горизонтальные — секущая плоскость параллельна горизонтальной плоскости проекции. Вертикальные — секущая плоскость перпендикулярна к горизонтальной плоскости проекции. Наклонные — секущая плоскость составляет с горизонтальной плоскостью 0%A3%D0%B3%D0%BE%D0%BB"угол, отличный от 0%9F%D1%80%D1%8F%D0%BC%D0%BE%D0%B9_%D1%83%D0%B3%D0%BE%D0%BB"прямого. 3. В зависимости от положения секущей плоскости относительно основных измерений предмета различают разрезы: Продольные — секущая плоскость направлена вдоль длины или высоты предмета. Поперечные — секущая плоскость перпендикулярна к длине или высоте предмета. 4. В зависимости от полноты изображения разрезы бывают: Полные — секущая плоскость пересекает весь предмет и изображение внутреннего его строения показывается по всему сечению. Местные — секущая плоскость пересекает только ту часть предмета, в которой требуется показать его внутреннюю форму. Границы местного разреза показываются тонкой сплошной волнистой линией. Местные разрезы не обозначают. 30. Правила нанесения размеров. Величину изображённой детали можно определять только по размерным числам. Их наносят над размерными линиями возможно ближе к их середине (рис. 4). Размерные линии 'Ограничивают стрелками, которые остриём должны касаться выносных линий (размеры 110, 30, 15, 0 20 и другие на рис. 4), линий контура (размер 040) или осевых линий. Размерную линию следует проводить параллельно отрезку, размер которого указывают по возможности вне контура изображения. Расстояние между параллельными размерными линиями и от размерной линии до параллельной ей линии контура берут от 7 до 10 мм. Нельзя допускать, чтобы размерные линии пересекались с выносными или являлись продолжением линий контура, осевых, центровых и выносных. Запрещается использовать линии контура, осевые, центровые и выносные в качестве размерных. Чтобы размерные линии не пересекались с выносными, меньший размер наносят ближе к изображению, а больший - дальше (размеры 15, 30 и размер 110 на рис. 4). Форма стрелки показана на рис. 5. Размер стрелок следует выдерживать приблизительно одинаковым на всём чертеже. Каждый размер на чертеже указывают только один раз. Размерные числа линейных размеров наносят в соответствии с положением размерных линий, как показано на рис. 6. Если размерная линия вертикальная, то размерное число ставят справа (рис. 6а). На наклонных размерных линиях цифры пишут так, чтобы они оказались в удобном для чтения положении, если дать размерной линии "упасть" в горизонтальное положение, как это указано стрелками на рис. 6 а, б, в. Линейные размеры на машиностроительных чертежах указывают в миллиметрах; если размеры нанесены у изображений, то единицы измерений (мм) не проставляют (см. рис.4). Угловые размеры наносят, как показано на рис. 7. Их указывают в градусах (°), минутах (') и секундах ("), проставляя единицы измерения, например, размер 30° на рис. 7. Размерную линию при этом проводят в виде дуги окружности с центром в вершине угла. Для обозначения диаметра перед размерным числом во всех случаях наносят знак - кружок, перечеркнутый прямой линией под углом 75°. Применение и построение этого знака показано на рис. 8. Для обозначения радиуса перед размерным числом всегда наносят знак R - латинская прописная буква (см. рис. 4). Стрелку наносят с одной стороны (см. рис. 9) Если деталь имеет несколько одинаковых отверстий или других элементов (кроме скруглений), то наносится размер одного из них, а количество отверстий или других элементов указывают перед размерным числом, например 3 отв. 16 (рис. 10а). 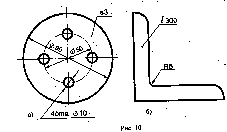 Размеры толщины или длины детали, форма которой задана одним видом, наносят, как показано на рис. 10. Перед числом, указывающим толщину детали, наносят букву S, а перед числом, указывающим длину детали, - букву L 31. Аксонометрические проекции. Окружность в аксонометрии. Изображение детали с вырезом ¼ . Аксонометрическая проекция - способ изображения геометрических предметов на чертеже при помощи параллельных проекций. При параллельном проецировании окружности на какую-нибудь плоскость П получаем ее изображение в общем случае в виде эллипса. Для передачи внутренних форм аксонометрию следует выполнять с вырезом передней 1/4 части предмета. Плоские фигуры, получаемые при этом, являются половинами фронтального и профильного разрезов. Сначала выполняется сечение в плоскости х'о'z' а затем в плоскости у'о'z'. Размеры координатных отрезков берутся с комплексного чертежа, при этом размеры по оси у сокращаются в два раза. Выполняется штриховка сечений, затем вычерчиваются эллипсы – диметрия окружностей, расположенных в горизонтальных плоскостях. Проводят контурные линии наружных и внутренних поверхностей и видимые линии их взаимного пересечения. Затем удаляются вспомогательные линии и обводится чертёж. 32. Построение разверток поверхности. Поверхность называется развертывающейся, если она путем изгибания может быть совмещена с плоскостью без образования складок и разрывов. При этом исходим из представления поверхности как гибкой, но нерастяжимой и несжимаемой пленки. Свойством развертываемости обладают многогранные поверхности и кривые линейчатые поверхности с ребром возврата: торсы, конические и цилиндрические. При построении развертки поверхности вращения ее разбивают с помощью меридианов на сравнительно узкие, равные между собой доли. Каждую такую долю аппроксимируют цилиндрической поверхностью, которая касается данной поверхности в точке среднего меридиана дали. Этот средний меридиан является нормальным сечением цилиндрической поверхности. Границами цилиндрической поверхности будут плоскости меридианов, ограничивающих рассматриваемую долю. |
