Навигация по странице: Если члены ряда (2) не больше соответствующих членов ряда (3), т.е. и ряд (3) сходится, то сходится и ряд (2). Если существует конечный и отличный от нуля предел, то ряды (2) и (3) сходятся или расходятся одновременно.Пример. Ряд 3. Если знакопеременный ряд1. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.Если степенной ряд сходится при некотором значении , то он абсолютно сходится при всяком значении xЕсли ряд расходится при некотором значении , то он расходится при всяком xТеорема., лежащей внутри интервала, ряд сходится абсолютно, для точек x , лежащих вне него – расходится. Число R – радиус сходимости степенного ряда.
|
Шпоргалка математика. 2. Пусть имеем два ряда с положительными членами (2) и (3). Теорема 1
14. Объем. Как отмечалось выше, объем цилиндроида, т.е. тела, ограниченного поверхностью 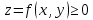 , плоскостью , плоскостью 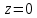 и цилиндрической поверхностью, направляющей для которой служит граница области D, а образующие параллельные оси и цилиндрической поверхностью, направляющей для которой служит граница области D, а образующие параллельные оси 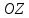 ,равен ,равен 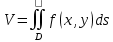
Пример. Вычислить объем тела, ограниченного поверхностями 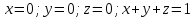 .Очевидно, что .Очевидно, что 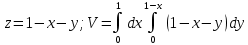 . .
Замечание 1. Если тело, объем которого ищется, ограничено сверху поверхностью 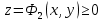 , а снизу – поверхностью , а снизу – поверхностью 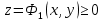 причем проекцией обеих поверхностей на плоскость причем проекцией обеих поверхностей на плоскость  является область D, то объем этого тела равен разности объемов двух цилиндроидов:. является область D, то объем этого тела равен разности объемов двух цилиндроидов:.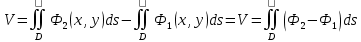 . Формула верна для любых непрерывных функций . Формула верна для любых непрерывных функций 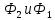 , для которых , для которых 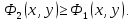
Площадь плоской фигуры.
Если составить интегральную сумму для функции 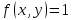 по области D, то эта сумма равна площади по области D, то эта сумма равна площади 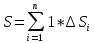 . Переходя к пределу, получим: . Переходя к пределу, получим: 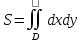 . Если область – правильная, то имеем . Если область – правильная, то имеем 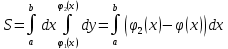 – формула, рассмотренная ранее. – формула, рассмотренная ранее.
Пример 2. Вычислить площадь, ограниченную линиями 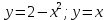 . Координаты точек пересечения: . Координаты точек пересечения: 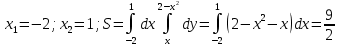
|
2. Пусть имеем два ряда с положительными членами:  (2) и (2) и  (3). (3).
Теорема 1. Если члены ряда (2) не больше соответствующих членов ряда (3), т.е. 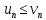 и ряд (3) сходится, то сходится и ряд (2). и ряд (3) сходится, то сходится и ряд (2).
Пусть 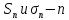 сумма рядов. Из сумма рядов. Из 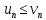 следует, что следует, что 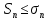 Т.к. ряд (3) сходится, то Т.к. ряд (3) сходится, то 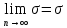 . Т.к. члены рядов положительны, то . Т.к. члены рядов положительны, то 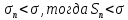 Доказали, что частичные суммы Доказали, что частичные суммы 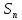 возрастают и ограничены, значит, они имеют предел: возрастают и ограничены, значит, они имеют предел: 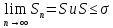
Пример. Ряд  сходится, т.к. его члены меньше соответствующих членов ряда. сходится, т.к. его члены меньше соответствующих членов ряда. 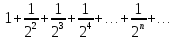 Последний ряд сходится, т.к. начиная со второго члена - это геометрическая прогрессия с Последний ряд сходится, т.к. начиная со второго члена - это геометрическая прогрессия с 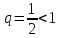
Теорема 2. Если члены ряда (2) не меньше соответствующих членов ряда (3), т.е. 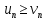 и ряд (3) расходится, то и ряд (2) расходится. Из условия и ряд (3) расходится, то и ряд (2) расходится. Из условия 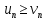 следует, что следует, что 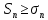 (положительный ряд). Т.к. ряд (3) расходится, то (положительный ряд). Т.к. ряд (3) расходится, то 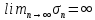 , тогда из , тогда из 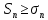 следует, что, следует, что, 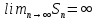 т.е. ряд (2) расходится. т.е. ряд (2) расходится.
Пример. Ряд  расходится, т.к его члены начиная со второго, больше соответствующих членов гармонического ряда расходится, т.к его члены начиная со второго, больше соответствующих членов гармонического ряда 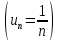 , который расходится. , который расходится.
Теорема 3. Если существует конечный и отличный от нуля предел, 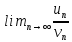 то ряды (2) и (3) сходятся или расходятся одновременно. то ряды (2) и (3) сходятся или расходятся одновременно.
|
6. Знакочередующиеся ряды.
Члены знакочередующегося ряда имеют чередующиеся знаки: 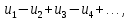 где где 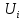 - положительны. - положительны.
Теорема Лейбница. Если в знакочередующемся ряде 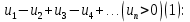 члены таковы, что члены таковы, что 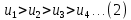 и и 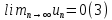 , то ряд (1) сходится, его сумма положительна и не превосходит , то ряд (1) сходится, его сумма положительна и не превосходит 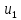 . Рассмотрим сумму . Рассмотрим сумму 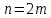 первых членов ряда (1): первых членов ряда (1): 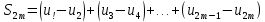 . Из (2) следует, что . Из (2) следует, что 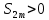 и возрастает с увеличением m. Запишем и возрастает с увеличением m. Запишем 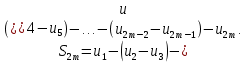 В силу (2) каждая скобка положительна. В результате вычитаний получим число, меньше В силу (2) каждая скобка положительна. В результате вычитаний получим число, меньше 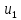 , т.е. , т.е. 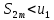 . . 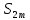 возрастает и ограниченна сверху возрастает и ограниченна сверху 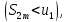 поэтому имеет предел S: поэтому имеет предел S: 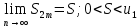 . Рассмотрим нечетные суммы: . Рассмотрим нечетные суммы: 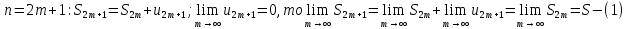 сходится. Замечание. Теорема Лейбница справедлива, если (2) выполняется, начиная с некоторого N. сходится. Замечание. Теорема Лейбница справедлива, если (2) выполняется, начиная с некоторого N.
Пример. Ряд 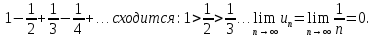
|
3. Теорема. Если в ряде с положительными членами  отношение отношение 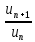 при при 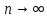 имеет конечный придел имеет конечный придел 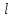 , т.е. , т.е. 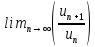 , то ряд сходится в случаи , то ряд сходится в случаи 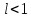 ряд расходится при. ряд расходится при. 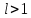 При При 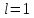 теорема не дает ответа о сходимости ряда. теорема не дает ответа о сходимости ряда.
Доказательство. Пусть 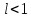 Рассмотрим число Рассмотрим число 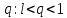 . По определению предела . По определению предела 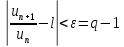 начиная с номера начиная с номера 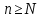 отсюда отсюда 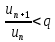 . Запишем последнее неравенство для . Запишем последнее неравенство для 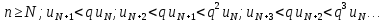
Рассмотрим два ряда: 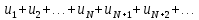 (1) и (1) и  Ряд Ряд  – геометрическая прогрессия с – геометрическая прогрессия с 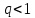 – сходится. Члены ряда (1), начиная с – сходится. Члены ряда (1), начиная с 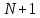 , меньше членов ряда , меньше членов ряда 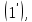 поэтому ряд (1) сходится на основании признака сравнения. поэтому ряд (1) сходится на основании признака сравнения.
Пусть 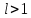 . Тогда из . Тогда из 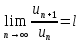 , , 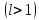 следует, что следует, что 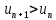 для для 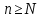 . Но это означает, что члены ряда возрастают и . Но это означает, что члены ряда возрастают и 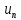 не стремится к 0, поэтому ряд расходится. не стремится к 0, поэтому ряд расходится.
Замечание 1.
Если 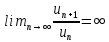 , то ряд расходится. , то ряд расходится.
Если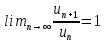 , но , но 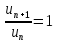 , начиная с , начиная с 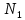 , то ряд расходится. , то ряд расходится.
|
4. Если для ряда с положительными членами  (1) величина (1) величина 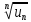 имеет конечный предел имеет конечный предел 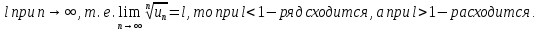
Пусть 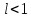 . Рассмотрим . Рассмотрим 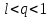 . Начиная с . Начиная с 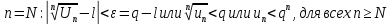 . Рассмотрим два ряда: . Рассмотрим два ряда: 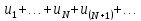 (1) и (1) и 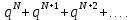 Ряд Ряд  сходится – геометрическая прогрессия с сходится – геометрическая прогрессия с 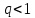 Члены ряда (1), начиная с Члены ряда (1), начиная с 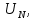 меньше членов ряда меньше членов ряда  ряд (1) сходится. ряд (1) сходится.
Пусть 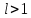 , тогда , тогда 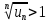 начиная с начиная с  или или 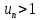 – ряд расходится, т.к. – ряд расходится, т.к. 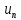 не стремится к нулю. не стремится к нулю.
Пример. 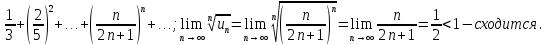
Замечание: Если 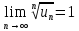 то требуется дальнейшие исследования. то требуется дальнейшие исследования.
Пример. Для гармонического ряда 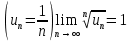 однако ряд расходится. однако ряд расходится.
Пример,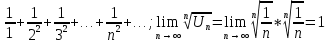 , но ряд сходится, т.к. члены ряда, начиная со второго, меньше членов сходящего ряда , но ряд сходится, т.к. члены ряда, начиная со второго, меньше членов сходящего ряда 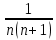 . .
|
19. Понятие события. Под случайным событием будем понимать все то, что может произойти, а может и не произойти при проведении испытаний. Например, стрелок стреляет по мишени. Выстрел это испытание, попадание в определенную область мишени – это случайное событие.
События обозначается заглавными латинскими буквами. Событие U называется достоверным, если оно обязательно происходит при каждом испытании.
Событие V называется невозможным, если оно не происходит не при каком испытании
20. Классическое определение вероятностей.
Пусть в урне имеются 3 белых, 2 черных одинаковых шара. Если наудачу извлекается шар, то возможно 5 элементарных исходов (можно вынуть любой из трех белых и любой из двух черных шаров). Такие исходы образуют полную группу, и они равновозможные (равновероятные), так как нет основания считать, что появление какого-либо шара будет предпочтительней. Мы рассмотрели все возможные исходы. Мы рассматриваем возможность вынуть белый шар, тогда интересующими нас исходами будет появление из 3 белых шаров. Эти исходы назовем благоприятствующими нашим событиям. Отношение благоприятствующих исходов к общему числу всех исходов называется вероятностью событий A и обозначается 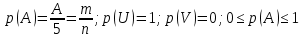 . События A и B называются несовместными, если их совместное наступление невозможно. События . События A и B называются несовместными, если их совместное наступление невозможно. События 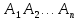 образуют полную группу, если они попарно не совместны и в результате испытания наступит одно и только одно событие. образуют полную группу, если они попарно не совместны и в результате испытания наступит одно и только одно событие.
|
7. Знакопеременный ряд 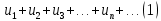 называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов 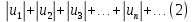 . Если ряд (1) сходится, а ряд (2) расходится, то знакопеременный ряд сходится условно. . Если ряд (1) сходится, а ряд (2) расходится, то знакопеременный ряд сходится условно.
Знакопеременные ряды – если среди членов есть положительные и отрицательные.
Числа 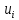 - положительные и отрицательные. - положительные и отрицательные.
Теорема. Если знакопеременный ряд 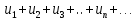 (1) таков, что ряд из модулей (1) таков, что ряд из модулей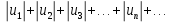 (2) сходится, то и данный ряд сходится. (2) сходится, то и данный ряд сходится.
Доказательство.
Пусть 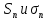 - суммы первых n членов рядов (1) и (2). - суммы первых n членов рядов (1) и (2).
Пусть  - сумма положительных членов, - сумма положительных членов, 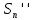 сумма модулей отрицательных членов, тогда сумма модулей отрицательных членов, тогда 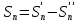 и и 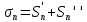 . По условию . По условию  имеет предел имеет предел 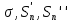 – положительные возрастающие величины, меньшие – положительные возрастающие величины, меньшие 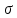 , поэтому они имеют пределы , поэтому они имеют пределы 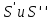 , тогда и , тогда и 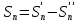 имеет предел имеет предел 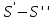 , т.е. (1) – сходится. Отметим следующие свойства абсолютно и условно сходящихся рядов. , т.е. (1) – сходится. Отметим следующие свойства абсолютно и условно сходящихся рядов.
1. Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой перестановке его членов. При этом сумма ряда не зависит от порядка его членов.
2. Если ряд сходится условно, то, какое бы ни выбрали число А, можно так переставить члены этого ряда, чтобы его сумма оказалась равной А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный после перестановки окажется расходящимся.
сумма ряда после перестановки уменьшилась вдвое. Это говорит о том, что бесконечные ряды отличаются по своим свойствам от сумм конечного числа слагаемых.
|
8. Ряд 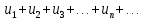 называется функциональным, если его члены являются функциями от X: называется функциональным, если его члены являются функциями от X: 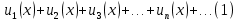 . Давая x определенные числовые значения, получим различные числовые ряды, которые могут сходиться и расходиться. Совокупность тех значений x, при которых функциональный ряд сходится, называется областью сходимости ряда. В области сходимости ряда его сумма является функцией . Давая x определенные числовые значения, получим различные числовые ряды, которые могут сходиться и расходиться. Совокупность тех значений x, при которых функциональный ряд сходится, называется областью сходимости ряда. В области сходимости ряда его сумма является функцией 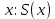 . .
Пример. 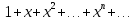 . Этот ряд сходится при . Этот ряд сходится при 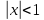 (убывающая геометрическая прогрессия). Очевидно, (убывающая геометрическая прогрессия). Очевидно, 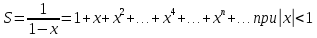 . Пусть . Пусть 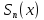 – сумма первых n членов ряда (1). Если этот ряд сходится и его сумма равна – сумма первых n членов ряда (1). Если этот ряд сходится и его сумма равна 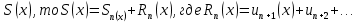 остаток ряда. Для всех х в области сходимости ряда остаток ряда. Для всех х в области сходимости ряда 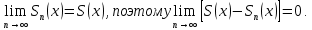
10. 1. Если степенной ряд 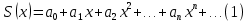 имеет интервал сходимости имеет интервал сходимости 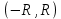 , то ряд , то ряд 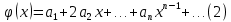 , полученный почленным дифференцированием ряда (1), имеет тот же интервал сходимости , полученный почленным дифференцированием ряда (1), имеет тот же интервал сходимости 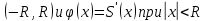 , т.е. внутри интервала сходимости производная от суммы ряда равна сумме производных от членов ряда. , т.е. внутри интервала сходимости производная от суммы ряда равна сумме производных от членов ряда.
Замечание. Полученный ряд снова можно почленно дифференцировать и продолжать сколько угодно раз.
2. Пусть дан ряд (1). Тогда 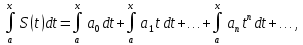 если если 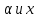 принадлежат интервалу сходимости принадлежат интервалу сходимости 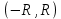 . Т.е. если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме интегралов от членов ряда . Т.е. если пределы интегрирования лежат внутри интервала сходимости степенного ряда, то интеграл от суммы ряда равен сумме интегралов от членов ряда
|
9. Степенным рядом называется функциональный ряд вида 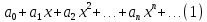 , где , где 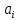 –числа – коэффициенты ряда. –числа – коэффициенты ряда.
Теорема Абеля.
Если степенной ряд сходится при некотором значении 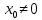 , то он абсолютно сходится при всяком значении x, для которого , то он абсолютно сходится при всяком значении x, для которого 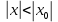 . .
Если ряд расходится при некотором значении 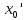 , то он расходится при всяком x, для которого , то он расходится при всяком x, для которого 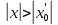 . .
Из теоремы Абеля следует, что если 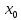 – точка сходимости, то весь интервал – точка сходимости, то весь интервал 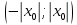 заполнен точками абсолютной сходимости, т.е. существует число R, такое что при всех х таких, что заполнен точками абсолютной сходимости, т.е. существует число R, такое что при всех х таких, что 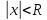 - степенной ряд сходится, а при - степенной ряд сходится, а при 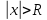 – расходится. – расходится.
Теорема. Областью сходимости степенного ряда является интервал с центром в начале координат.
Определение. Интервалом сходимости степенного ряда называется такой интервал от R до R, что для всякой точки x, лежащей внутри интервала, ряд сходится абсолютно, для точек x, лежащих вне него – расходится. Число R – радиус сходимости степенного ряда.
Для определения радиуса сходимости R применяют признаки Даламбера и Коши для модулей членов ряда. Для определения R используем признак Даламбера для модулей: 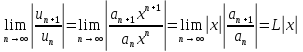 . .
|
5. Пусть члены ряда  положительны и не возрастают, т.е. положительны и не возрастают, т.е. 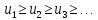 и пусть и пусть 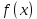 - такая - такая
н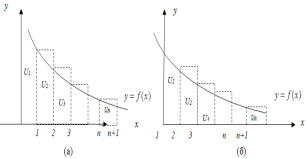 епрерывная невозрастающая функция, что епрерывная невозрастающая функция, что 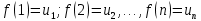 . Тогда ряд . Тогда ряд  и несобственный интеграл и несобственный интеграл 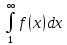 сходятся или расходятся одновременно. Построим графики членов ряда: Из графика (а) следует, что площади прямоугольников равны сходятся или расходятся одновременно. Построим графики членов ряда: Из графика (а) следует, что площади прямоугольников равны 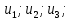 и т.д. и и т.д. и 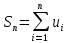 . С другой стороны, площадь области, ограниченной кривой . С другой стороны, площадь области, ограниченной кривой 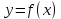 и прямыми и прямыми 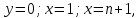 равна равна 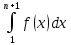 , поэтому , поэтому 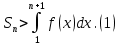
Из рисунка (б) следует, что сумма площадей всех прямоугольников равна 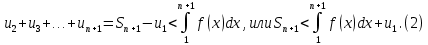 . Предположим, что . Предположим, что 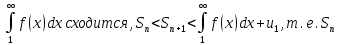 остается ограниченной остается ограниченной 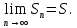
Пусть 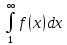 расходится, тогда расходится, тогда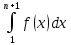 неограниченно возрастает при увеличении n. Тогда (из неравенства (1)) неограниченно возрастает при увеличении n. Тогда (из неравенства (1)) 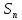 тоже неограниченно возрастает, т.е. ряд расходится. Пример. Ряд Дирихле: тоже неограниченно возрастает, т.е. ряд расходится. Пример. Ряд Дирихле: 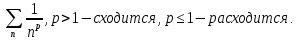
| |
|
|
 Скачать 326.99 Kb.
Скачать 326.99 Kb.