Шпоргалка математика. 2. Пусть имеем два ряда с положительными членами (2) и (3). Теорема 1
 Скачать 326.99 Kb. Скачать 326.99 Kb.
|
|
Пусть ряд 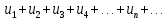 сходится, т.е. сходится, т.е. 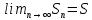 – сумма ряда. Тогда – сумма ряда. Тогда 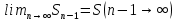 . Вычтем из одного другое: . Вычтем из одного другое: 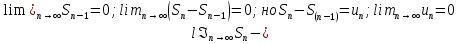 Следствие. Если Следствие. Если 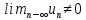 , то ряд расходится , то ряд расходится | 23. Теоремы умножения вероятностей Произведением событий А и B называется событие C состоящее осуществлением и события A и события B. C=AB. Условной вероятностью события A относительно события B 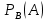 называется вероятность события A, найденное в предположении, что событие B уже произошло. называется вероятность события A, найденное в предположении, что событие B уже произошло.Пример. В урне 6 белых и 5 черных шаров на удачу вынимают последовательно 2 шара найти вероятность того что второй шар черный, если 1 извлеченный шар белый. Пусть событие 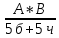 событие B второй извлеченный шар черный, тогда вероятность этого события. событие B второй извлеченный шар черный, тогда вероятность этого события. Теорема: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое событие произошло: 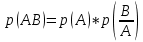 1. На пяти карточках записаны буквы О Л О В О, карточки извлекают на удачу извлекают по одной и выкладывают в линию. Найти вероятность того, что получится данное слово. Событие A. 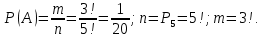 2. Среди 17 студентов группы, в которой 9 юношей производится розыгрыш 7 билетов лотереи, причем каждый студент может выбрать только один билет. Какова вероятность того, что среди обладателей билетов будет 4 девушки. 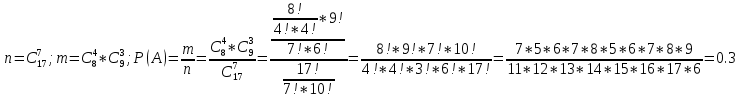 Теорема: Вероятность произведения двух независимых событий равно произведению их вероятностей 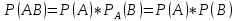 | 15. Якобиан преобразования имеет вид, где 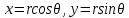 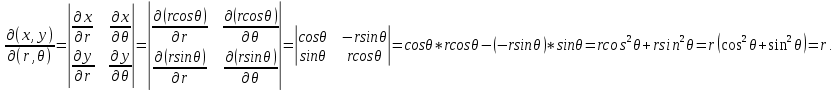 Следовательно, дифференциальный элемент в полярных координатах будет равен Следовательно, дифференциальный элемент в полярных координатах будет равен 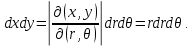 Пусть область интегрирования R в полярных координатах определяется следующим образом (рис 2) Пусть область интегрирования R в полярных координатах определяется следующим образом (рис 2) 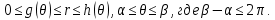 Тогда двойной интеграл в полярных координатах описывается формулой Тогда двойной интеграл в полярных координатах описывается формулой 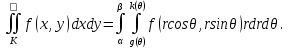 Полученную область (рис 3) будем называть полярным прямоугольником и удовлетворяющую условиям Полученную область (рис 3) будем называть полярным прямоугольником и удовлетворяющую условиям 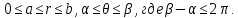 В этом случае формула замены переменных в двойном интеграле имеет вид В этом случае формула замены переменных в двойном интеграле имеет вид 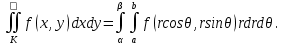  | 24. Вероятность появления хотя бы одного события 2 стрелка стреляют по мишени вероятность попадания 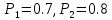 соответственно. Найти вероятность хотя бы одного попадания. Пусть событие А это хотя бы одно попадание. Вероятность этого события, что попал один соответственно. Найти вероятность хотя бы одного попадания. Пусть событие А это хотя бы одно попадание. Вероятность этого события, что попал один 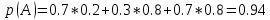 . Рассмотрим событие противоположное А: . Рассмотрим событие противоположное А: 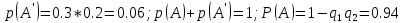 . Пусть в результате испытания могут появиться n независимых событий либо некоторые из этих событий, либо не одного. Пусть нам известны вероятности появления каждого события . Пусть в результате испытания могут появиться n независимых событий либо некоторые из этих событий, либо не одного. Пусть нам известны вероятности появления каждого события 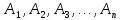 которые обозначим соответственно обозначим. Мы хотим найти вероятность появления хотя бы одного из этих событий. Рассмотрим противоположное событие, которое состоит в том, что не произошло не одно из событий которые обозначим соответственно обозначим. Мы хотим найти вероятность появления хотя бы одного из этих событий. Рассмотрим противоположное событие, которое состоит в том, что не произошло не одно из событий 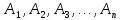 . Вероятность противоположного события . Вероятность противоположного события 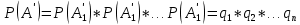 где где 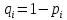 вероятность не появления вероятность не появления 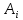 так как тема вероятностей противоположных событий равна 1. Вероятность появления хотя бы одного из событий так как тема вероятностей противоположных событий равна 1. Вероятность появления хотя бы одного из событий 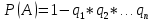 Теорема: Вероятность появления хотя бы одного из событий 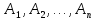 равна разности между единицей и произведением вероятностей противоположных событий: равна разности между единицей и произведением вероятностей противоположных событий: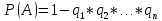 Следствие: Если События Следствие: Если События 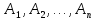 имеют одинаковую вероятность p, то вероятность появления хотя бы одного события имеют одинаковую вероятность p, то вероятность появления хотя бы одного события 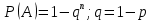 | 21. Элементы комбинаторики Комбинаторика рассматривает подсчет количества способов, выбора определенного количества элементов по определенным правилам. Различают размещения перестановки и сочетания. Размещениями называют комбинации, составленные из m элементов взятых из общего количества n, которое обличается либо составом элементов, либо порядком. Число размещений 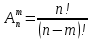 ; Перестановкой называется размещение из m элементов по n ; Перестановкой называется размещение из m элементов по n 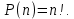 . Сочетаниями называются комбинации из n элементов по m, которые обличаются хотя бы одним элементом (порядок исследования не играет роли). . Сочетаниями называются комбинации из n элементов по m, которые обличаются хотя бы одним элементом (порядок исследования не играет роли). 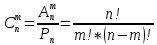 ; Размещениями с повторениями называют упорядоченные последовательности, составленные из n элементов по m в каждом, где некоторые элементы могут быть одинаковы. ; Размещениями с повторениями называют упорядоченные последовательности, составленные из n элементов по m в каждом, где некоторые элементы могут быть одинаковы. 22. Геометрическая и статическая вероятности. Классическое определение вероятности дает возможность рассматривать события, которые распадаются на конечное число равновероятных случаях. если количество равновероятных исходов большое, то используют геометрическую вероятность. Пусть имеется отрезок длиной L, внутри которого имеется отрезок длиной l. На отрезок 4 ставится точка. Считается, что вероятность попадания на отрезок l пропорциональна длине отрезка 4. Тогда вероятность попадания этой точки на отрезке l P(A)=l/L. Иногда удобно использовать отношение площадей P(A)=S^'/S. Относительная частота это отношение числа появления события A m к общему числу испытаний n (…m/n). Если число испытаний n неограниченно возрастает, то частость стремится к вероятности события |
| 27. Формула Байеса Пусть имеется полная группа гипотез вероятности, которых 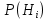 известны до опыта. Проводятся, в результате, которого появляется событие А. известно, что этому событию А гипотезы предписывали определенные условные вероятности известны до опыта. Проводятся, в результате, которого появляется событие А. известно, что этому событию А гипотезы предписывали определенные условные вероятности 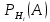 . Определим какими стали вероятности этих гипотез после опыта. . Определим какими стали вероятности этих гипотез после опыта. Исходя из того, что событие А произошло, необходимо переоценить приятности гипотез, то есть определить условную вероятность 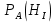 . . 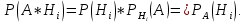 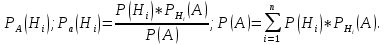  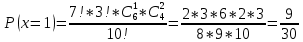 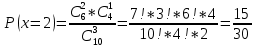 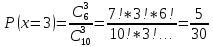 | 26. Формула полной вероятности Пример: на конвейер поступает продукция 3 станков. Причем 50% продукции изготавливает первый станок, 30% второй станок и 20% третий. Для 1 станка брак составляет 2%, для 2 3% и для 3 5%. Найти вероятность того, что наудачу взятая деталь будет доброкачественная. Событие A взятая деталь – доброкачественная. Вероятности изготовления стандартной детали 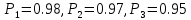 . вероятность того, что деталь изготовлена первым станком равна 0,5, на втором 0,3, на третьем 0,2. . вероятность того, что деталь изготовлена первым станком равна 0,5, на втором 0,3, на третьем 0,2. 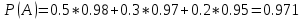 . пусть событие А может произойти в результате появления одного и только одного. События . пусть событие А может произойти в результате появления одного и только одного. События 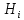 из общей группы несовместных событий. Тогда события из общей группы несовместных событий. Тогда события 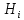 называются гипотезами называются гипотезами Теорема. Вероятность события А, которое может наступить при появлении одной из гипотез 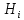 равна сумме парных произведений вероятностей всех гипотез на соответствующие условные вероятности события А равна сумме парных произведений вероятностей всех гипотез на соответствующие условные вероятности события А 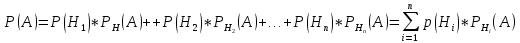 . Доказательство: событие А равносильно тому, что произойдет . Доказательство: событие А равносильно тому, что произойдет 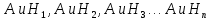 . . 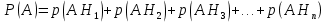 | 27. Событие А называется независимым в данной системе испытаний, если вероятность этого события в каждом из них не зависит от исходов других испытаний. Тогда считаем, что вероятность появления события А в каждом испытании постоянна и равна p. Определим вероятность 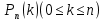 того, что при n независимых испытаниях событие А, имеющее одну и ту же вероятность р для каждого отдельного испытания, появится ровно k раз, безразлично в какой последовательности. Для каждого испытания имеется два исхода: А и того, что при n независимых испытаниях событие А, имеющее одну и ту же вероятность р для каждого отдельного испытания, появится ровно k раз, безразлично в какой последовательности. Для каждого испытания имеется два исхода: А и 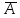 . Значит, если событие А встречается k раз, то . Значит, если событие А встречается k раз, то 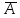 – (n – k) раз. Вероятность реализации такой благоприятной серии: – (n – k) раз. Вероятность реализации такой благоприятной серии: 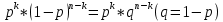 Все благоприятные серии получаются в результате выбора различных k номеров из общего числа n, т.е. Все благоприятные серии получаются в результате выбора различных k номеров из общего числа n, т.е. 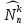 . Напомним, что число сочетаний . Напомним, что число сочетаний 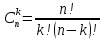 . Тогда по теореме сложения для несовместных событий: . Тогда по теореме сложения для несовместных событий: 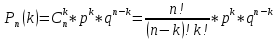 | 25. Суммой или объединением A и B называется событие C, состоящее в наступлении события A, или события B или событий A и B вместе: C=A+B. Теорема. Вероятность суммы конечного числа несовместных событий равна сумме их вероятностей. Докажем для двух событий. Пусть из общего числа n случаев событию A благоприятствует k случаев, а событию 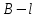 случаев. Тогда случаев. Тогда 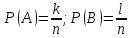 ; По условию события A и B несовместимы. Следовательно, ни один из k случаев, благоприятствующих A, не благоприятствующих B. Сумме ; По условию события A и B несовместимы. Следовательно, ни один из k случаев, благоприятствующих A, не благоприятствующих B. Сумме 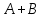 благоприятствующим благоприятствующим 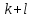 случаев из n, поэтому случаев из n, поэтому 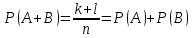 (доказательством является диаграмма Виена). (доказательством является диаграмма Виена).Следствие1: Сумма вероятностей событий, образующих полную группу, равна 1. Следствие2: Сумма вероятностей противоположных событий равна 1, 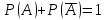 | 29. Локальная теорема Лапласа. Формула Пуассона Если число испытаний n велико (n > 20), то вычисления по формуле Бернулли громоздкие. Например, 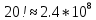 . Лаплас получил приближенную формулу: . Лаплас получил приближенную формулу: 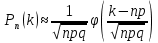 , где , где 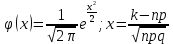 . Функция . Функция 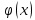 табулированная, т.е. имеется таблица значений функции. табулированная, т.е. имеется таблица значений функции.Очевидно, что 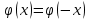 – функция четная. – функция четная.Пример. Вероятность поражения цели стрелком при одиночном выстреле 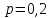 . Найти вероятность того, что из 100 выстрелов будет ровно 20 попаданий. . Найти вероятность того, что из 100 выстрелов будет ровно 20 попаданий.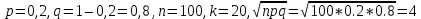 . .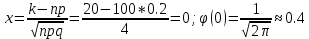 (таблица 1), тогда (таблица 1), тогда 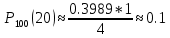 Вероятность малая, поскольку ровно 20 раз. Почти достоверное событие - около 20 раз. Если 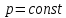 , но близка к нулю, а n достаточно велико, причем , но близка к нулю, а n достаточно велико, причем 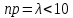 , то вероятность того, что в n испытаниях событие A наступит k раз , то вероятность того, что в n испытаниях событие A наступит k раз 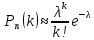 |
| 30. Интегральная теорема Лапласа Часто необходимо найти вероятность того, что число появлений события А заключено в интервале 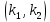 , т.е. число появлений события А в nиспытаниях не менее k1 и не более , т.е. число появлений события А в nиспытаниях не менее k1 и не более 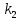 раз. Считаем, что вероятность появления события А раз. Считаем, что вероятность появления события А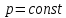 .Ответ дает интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность равна .Ответ дает интегральная теорема Лапласа. Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность равна 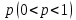 , событие наступит не менее k1 раз, и не более k2 раз, приблизительно равно , событие наступит не менее k1 раз, и не более k2 раз, приблизительно равно 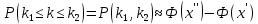 , где , где 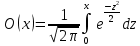 – функция Лапласа, которая табулирована; – функция Лапласа, которая табулирована; 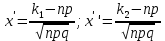 . Функция Лапласа . Функция Лапласа 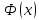 – нечетная: – нечетная: 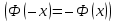 , возрастающая, для , возрастающая, для 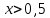 можно считать, что можно считать, что 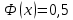 . .Следствие. Если вероятность р наступления события А – постоянна 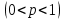 , а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях абсолютная величина отклонения относительной частоты события А от его вероятности р не превзойдет данного , а число испытаний достаточно велико, то вероятность того, что в n независимых испытаниях абсолютная величина отклонения относительной частоты события А от его вероятности р не превзойдет данного 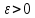 , находится по формуле , находится по формуле 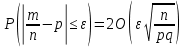 . Т.к . Т.к 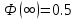 , то , то 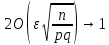 при при 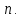 В условиях Бернулли, как бы ни было мало В условиях Бернулли, как бы ни было мало 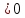 , с вероятностью, сколь угодно близкой к 1, можно ожидать, что при , с вероятностью, сколь угодно близкой к 1, можно ожидать, что при 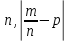 будет меньше будет меньше  (закон больших чисел в форме Бернулли). (закон больших чисел в форме Бернулли). | 31. Понятие случайной величины. Закон распределения дискретной случайной величины На практике часто встречаются величины, которые могут принимать некоторые значения, но нельзя достоверно предсказать, какое именно значение каждая из них примет в рассмотренном испытании. Например, число мальчиков, родившихся в Белгороде завтра, может быть различным: 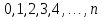 . Или – дальность полета снаряда, количество бракованных изделий в партии и т.д. Это – случайные величины. Случайной величиной называется переменная, которая может принимать те или иные значения, причем для каждого испытания она принимает единственное значение. Случайные величины обозначают заглавными буквами X, Y, Z, значения случайных величин соответственно малыми буквами. Случайные величины делятся на дискретные и непрерывные. Случайная величина называется дискретной, если множество ее значений конечно или счетное. Например, стрельба по мишеням из орудия до первого попадания (1,2,3,…, n, ). Или – количество бракованных деталей в партии из 30 изделий. . Или – дальность полета снаряда, количество бракованных изделий в партии и т.д. Это – случайные величины. Случайной величиной называется переменная, которая может принимать те или иные значения, причем для каждого испытания она принимает единственное значение. Случайные величины обозначают заглавными буквами X, Y, Z, значения случайных величин соответственно малыми буквами. Случайные величины делятся на дискретные и непрерывные. Случайная величина называется дискретной, если множество ее значений конечно или счетное. Например, стрельба по мишеням из орудия до первого попадания (1,2,3,…, n, ). Или – количество бракованных деталей в партии из 30 изделий. |
