методичка. Методические указания_Правила построения гистограмм. Правила построения гистограмм

• Название: Правила построения гистограмм
• Анкор: методичка
• Дата: 06.10.2022
• Размер: 75.07 Kb.
• Имя файла: Методические указания_Правила построения гистограмм.docx
• Тип: Правила; #717631

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

Правила построения гистограмм

Практическое задание 1:

Одним из способов представления и анализа случайных величин является построение гистограмм распределения. Гистограмма показывает, как часто встречаются те или иные значения случайной величины, по ней можно качественно оценить функцию плотности распределения.

Рассмотрим правило построения гистограмм на конкретном примере.
Работа с преподавателем.

Задача: Даны значения пульса у 25 испытуемых (объем выборки n=25). Представить выборку в виде таблицы частот и построить гистограмму.
70 75 63 64 72 77 80 85 79 64 63 60 55 56 58 58 73 72 65 65 66 68 69 66 68
Необходимо выполнить следующие шаги:

1. 
   Элементы выборки объемом n=25 расположить в ранжированный ряд (по возрастанию или убыванию)
   

55 56 58 58 60 63 63 64 64 65 65 66 66 68 68 69 70 72 72 73 75 77 79 80 85

2. 
   Вычислить размах R (разность между минимальным и максимальным значением случайной величины):
   

R=x_max-x_min=85-55=30 уд/мин

3. 
   Разбить вариационный ряд на k непересекающихся интервалов. k вычисляют по формуле Стерднесса, предусматривающей выделение оптимального числа интервалов:
   

k=1+3.322lg(n) (округлить до целого)

Можно воспользоваться следующими рекомендациями

Объем выборки	Число интервалов
25-40	5-6
41-60	6-8
61-100	7-10
101-200	8-12
Более 200	10-15

Т.к. в нашем случае объем выборки равен 25, то возьмем k=6.

4. 
   Определить длину одного интервала:
   

b=R/k=30/6=5 уд/мин

5. 
   Определить границы каждого интервала
   
6. 
   Определить частоты - количество ni элементов выборки, попавших в i-й интервал (элемент, совпадающий с правой границей интервала, относится к последующему интервалу)
   

Наряду с частотами одновременно подсчитываются также относительные частоты 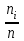и процент случаев относительно общего объема выборки



Полученные результаты сводятся в таблицу, называемую таблицей частот группированной выборки.

Для нашей задачи результаты группировки представлены в следующей таблице:

Номер интервала, i	Границы интервала	Частота, ni	Относительная частота	Процент случаев
1	55-60	4	0,16	16
2	60-65	5	0,20	20
3	65-70	7	0,28	28
4	70-75	4	0,16	16
5	75-80	3	0,12	12
6	80-85	2	0,08	8
	ИТОГО	Σ=25	Σ=1	Σ=100%

7. 
   Далее строится гистограмма. По оси абсцисс откладываются интервалы, по оси ординат могут откладываться абсолютная частота встречаемости, или относительная частота встречаемости, или же процент относительно общего объема выборки.
   

В данном случае исследуемый признак – это пульс, который является случайной величиной X (x₁, x₂, x₃ …..x_i…… x_n)




Этот график дает нам информацию о законе распределения случайной величины и носит название гистограммы распределения. Он показывает, насколько часто встречаются те или иные значения случайной величины.

По оси ординат могут откладываться

• 
  Абсолютная частота встречаемости
  
• 
  Процент относительно общего объема выборки
  

• 
  Относительная частота встречаемости
  

Огибающая гистограммы дает нам качественное представление о законе распределения случайной величины (иногда просто говорят распределение). Этот закон характеризует вероятность того, что случайная величина примет то или иное значение. Существует множество различных законов распределения. Наиболее распространенным является нормальное распределение – оно имеет симметричный колоколообразный вид.

Какую информацию дает нам этот график.

• 
  Самое низкое значение пульса лежит в пределах 55-60 уд/мин (Xmin)
  
• 
  Самый высокий пульс – в пределах 80-85 уд/мин (Xmax)
  
• 
  Люди с высоким и низким значениями давления встречаются реже, чем люди с нормальными значениями. Так, пульс в пределах 55-60 уд/мин встречается в 16% случаев, пульс 80-85 уд/мин встречается в 8% случаев.
  
• 
  Наиболее часто встречается пульс от 65 до 70 уд/мин (28% случаев)
  
• 
  Наиболее редко встречается пульс от 80 до 85 уд/мин (8 % случаев)
  
• 
  Норма (60-80 уд/мин) наблюдается у 76% обследованных