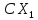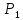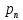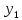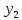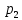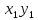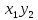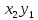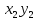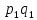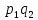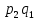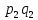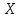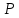Шпоргалка математика. 2. Пусть имеем два ряда с положительными членами (2) и (3). Теорема 1
 Скачать 326.99 Kb. Скачать 326.99 Kb.
|
|
Непрерывной называют случайную величину, которая может принимать все значения из некоторого конечного (или бесконечного) промежутка. Пусть Х – дискретная случайная величина, возможными и единственными значениями которой являются х1, х2, х3,…, хn. Обозначим через 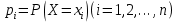 вероятность этих значений, т.е. рi есть вероятность того, что Х принимает значения xi. События Х = хi образует полную группу, поэтому вероятность этих значений, т.е. рi есть вероятность того, что Х принимает значения xi. События Х = хi образует полную группу, поэтому 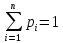 Закон распределения дискретных случайных величин – соответствие между всеми значениями дискретных случайных величин и их вероятностями. Обычно его записывают в виде таблицы: Закон распределения дискретных случайных величин – соответствие между всеми значениями дискретных случайных величин и их вероятностями. Обычно его записывают в виде таблицы:
Если множество xi – бесконечно, то ряд 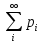 - сходится. - сходится. | 32.33. Математическое ожидание дискретной случайной величины и его свойства Закон распределения полностью описывает случайную величину, однако иногда выгоднее пользоваться числами, которые описывают случайную величину суммарно – это числовые характеристики величин. Рассмотрим математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. Пусть дискретная случайная величина принимает значения 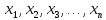 с вероятностями с вероятностями 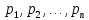 , тогда , тогда 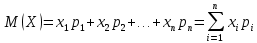 . Если дискретная случайная величина X принимает счетное множество возможных значений, то . Если дискретная случайная величина X принимает счетное множество возможных значений, то  , причем М(Х) существует, если ряд сходится абсолютно. М(Х) – неслучайная (постоянная) величина. Свойства М(Х) , причем М(Х) существует, если ряд сходится абсолютно. М(Х) – неслучайная (постоянная) величина. Свойства М(Х)1. Математическое ожидание постоянной величины равно самой постоянной, т.е 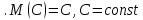 . .С имеет одно значение, равное С, с вероятностью 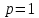 , , 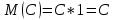 . Определим произведение постоянной С на Х как дискретную случайную величин . Определим произведение постоянной С на Х как дискретную случайную величин 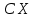 , возможные значения которой равны произведениям С на возможные значения Х. Вероятность , возможные значения которой равны произведениям С на возможные значения Х. Вероятность 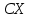 равна вероятностям Х. Например, если равна вероятностям Х. Например, если 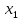 имеет вероятность имеет вероятность 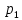 , то , то 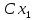 имеет также вероятность имеет также вероятность 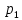 . .2. 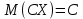 . М(Х) – константу можно выносить за знак математического ожидания. Пусть случайная дискретная величина X задана законом распределения: . М(Х) – константу можно выносить за знак математического ожидания. Пусть случайная дискретная величина X задана законом распределения:
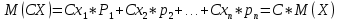 Случайные величины X и Y называют независимыми, если закон распределения одной из них не зависит от того, какие значения принимает другая. Произведение 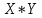 – случайная величина XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y. Вероятности XY равны произведению соответствующих вероятностей X и Y. – случайная величина XY, возможные значения которой равны произведениям каждого возможного значения Х на каждое возможное значение Y. Вероятности XY равны произведению соответствующих вероятностей X и Y.3. 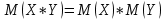 , где X, Y – независимые дискретные случайные величины. Пусть законы распределения вероятностей этих величин: , где X, Y – независимые дискретные случайные величины. Пусть законы распределения вероятностей этих величин:
Составим значения, которые могут принимать 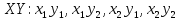 Закон распределения: Закон распределения:
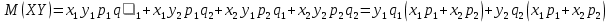 4. 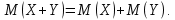 Возможные значения случайной величины X + Y равна сумме возможных значений X и Y , а вероятность X+Y равна произведению вероятностей слагаемых. Возможные значения случайной величины X + Y равна сумме возможных значений X и Y , а вероятность X+Y равна произведению вероятностей слагаемых.Теорема. М(Х) числа появлений событий А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в одном испытании p. Иначе, М(Х) биноминального распределения равно 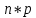 . . | 34. Дисперсия случайной дискретной величины и ее свойства. Легко указать случайные величины, имеющие одинаковые значения математических ожиданий, но различные возможные значения, например:
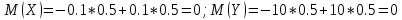 Х имеет возможные значения, близкие к математическому ожиданию, а Y – далекие от М(Y), таким образом, М(Х) полностью не характеризует Х. Надо охарактеризовать отклонение случайной величины от M(X): отклонение – это величина X – M(X). Х имеет возможные значения, близкие к математическому ожиданию, а Y – далекие от М(Y), таким образом, М(Х) полностью не характеризует Х. Надо охарактеризовать отклонение случайной величины от M(X): отклонение – это величина X – M(X).Теорема. Математическое ожидание отклонения равно нулю. Действительно, 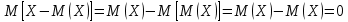 ,поэтому для оценки отклонения берут квадрат отклонения. ,поэтому для оценки отклонения берут квадрат отклонения.Дисперсией (рассеянием) дискретных случайных величин называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания:  . . Получаем: 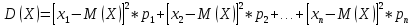 Свойства дисперсии 1. Дисперсия постоянной величины равной нулю. 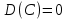 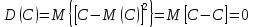 . .2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: 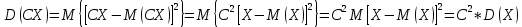 . Если . Если 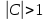 , то величина СХ имеет большие (по модулю) значения, поэтому , то величина СХ имеет большие (по модулю) значения, поэтому 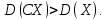 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин 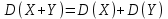 . Докажем: . Докажем: 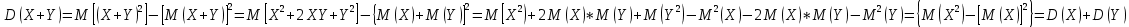 Следствие: Следствие: 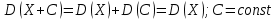 . .4. 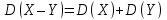 . Докажем: . Докажем: 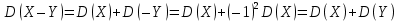 . .Теорема. Дисперсия числа появлений событий А в n независимых испытаниях, в каждом из которых вероятность появления события А 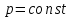 , равна , равна 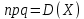 ,где ,где 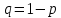 . Иначе. Дисперсия биноминального распределения равна . Иначе. Дисперсия биноминального распределения равна 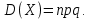 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35. Дискретная случайная величина может быть задана перечислением всех ее возможных значений и их вероятностей – законом распределения. Но его нельзя использовать для задания непрерывных случайных величин. Необходим общий способ задания случайных величин - это функция распределения вероятностей случайных величин. Пусть x – действительное число. Вероятность того, что случайная величина Х примет значение, меньше x, т.е. 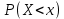 обозначим через обозначим через 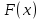 . Если x изменяется, то изменяется и . Если x изменяется, то изменяется и 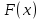 , т.е. , т.е. 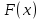 – функция х. Функцией распределения называют функцию – функция х. Функцией распределения называют функцию 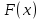 , определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньше x, т.е. , определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньше x, т.е. 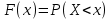 . Геометрически . Геометрически 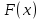 есть вероятность того, что случайная величина примет значение, которое изображается точкой левее точки х. есть вероятность того, что случайная величина примет значение, которое изображается точкой левее точки х.Добавим более четкое определение непрерывной случайной величины – случайная величина называется непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной. Свойства F(x) Значения функции распределения принадлежат отрезку 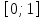 , т.е. , т.е. 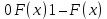 вероятность, вероятность, 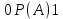 . .F(x) неубывающая функция, т.е. 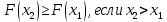 . Пусть . Пусть 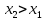 . Событие, состоящее в том, что Х примет значение меньше . Событие, состоящее в том, что Х примет значение меньше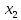 , можно разделить на 2 несовместных события: , можно разделить на 2 несовместных события:Х примет значение, меньше 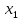 , с вероятностью , с вероятностью 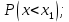 Х примет значение  с вероятностью с вероятностью 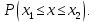 По теореме сложения: По теореме сложения: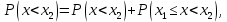 отсюда: отсюда: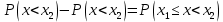 или или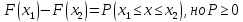 Следствие 1. Вероятность того, что 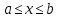 равна приращению равна приращению 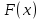 на этом интервале: на этом интервале: 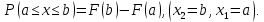 Следствие 2. Вероятность того, что случайная величина Х примет одно определенное значение равна 0. 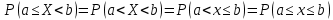 Если возможные значения случайной величины (a,b), то: 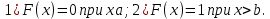 Докажем. Если 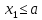 , то события , то события 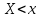 невозможны. Пусть невозможны. Пусть 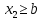 , тогда , тогда 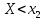 – достоверное событие. – достоверное событие.Следствие. Если значения непрерывной случайной величины расположены на всей числовой оси, то 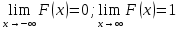 . . | 36. Плотность распределения вероятностей непрерывной | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||