МИНОБРНАУКИ РОССИИ. Курсовая работа Метод МонтеКарло в информационной безопасности

• Название: Курсовая работа Метод МонтеКарло в информационной безопасности
• Дата: 27.01.2022
• Размер: 1.18 Mb.
• Имя файла: МИНОБРНАУКИ РОССИИ.docx
• Тип: Курсовая; #344238

МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования «МИРЭА – Российский технологический университет» РТУ МИРЭА
	Институт кибернетики
	Курсовая работа Метод Монте-Карло в информационной безопасности
	по дисциплине «Теория принятия решений в условиях информационных конфликтов » (7 семестр)
Отчет представлен к рассмотрению:
Студент группы КТСО-03-18			«»   2021 г.	.
				(подпись и расшифровка подписи)
Руководитель курсовой работы			«»   2021 г.
				(подпись и расшифровка подписи)

Москва 2021

Оглавление

Федеральное государственное бюджетное образовательное учреждение 1

высшего образования 1

«МИРЭА – Российский технологический университет» 1

РТУ МИРЭА 1

Введение 3

Общая схема метода Монте-Карло. 4

Точность вычислений 5

Численный пример 8

Численный пример: a=0; b=pi/2; g(x) = cos(x). 8

Вычислим значение интеграла с применением двух различных случайных величин. 8

В первом случае используем равномерно распределенную случайную величину на [a,b], т.е.  8

Количество итераций и генераторы случайных чисел 9

Метод Монте-Карло в информационной безопасности 11

Постановка задачи и игровой подход 11

Для поиска наиболее оптимального набора средств защиты компьютерной системы можно провести математическую игру двух сторон, одной из которых является система защиты компьютерной̆ информации (I игрок – администратор), а с другой – возможные атаки хакеров (II игрок – злоумышленник). Один из подходов, моделирующий игру хакера и администратора безопасности, основан на теории позиционных игр. 11

Нахождение оптимальной стратегии администратора безопасности методом Монте-Карло 14

Оптимизация симуляций 16

Реализуемый алгоритм USB1 17

Описание программного продукта и анализ результатов расчёта 18

Заключение 22

Список использованной литературы 23

Введение 3

Общая схема метода Монте-Карло. 4

Точность вычислений 5

Численный пример 7

Количество итераций и генераторы случайных чисел 9

Метод Монте-Карло в информационной безопасности 10

Постановка задачи и игровой подход 10

Нахождение оптимальной стратегии администратора безопасности методом Монте-Карло 13

Оптимизация симуляций 15

Реализуемый алгоритм USB1 15

Описание программного продукта и анализ результатов расчёта 16

Заключение 21

Литература 22

Введение

Цель работы заключается в рассмотрении метода Монте-Карло как одного из способов решения задач с помощью моделирования случайных величин или случайных процессов, а также применение рассмотренного метода в решении некоторых практических задач в информационной безопасности.

Моделирование Монте-Карло, также известное как метод Монте-Карло или многократное имитационное моделирование вероятностей, представляет собой математический метод, с помощью которого можно оценить возможные результаты неопределенного события. Метод Монте-Карло был изобретен Джоном фон Нейманом и Станиславом Уламом во время Второй мировой войны с целью улучшения процесса принятия решений в условиях неопределенности. Название методу дал известный своими казино город Монако, поскольку в основе данного подхода к моделированию лежит принцип генерации случайных чисел, применяемый в рулетке. Метод моделирования Монте-Карло нашел свое применение в оценке риска для разнообразных практических задач, включая искусственный интеллект, котировки акций, прогнозирование продаж, управление проектами и ценообразование. Кроме того, данный метод обладает рядом преимуществ по сравнению с прогнозными моделями с фиксированными входными значениями, включая возможность проведения анализа чувствительности или расчета корреляции входных значений. Анализ чувствительности позволяет оценить влияние отдельных входных значений на определенный результат, а корреляция — понять взаимосвязи между любыми входными переменными. Моделирование по методу Монте Карло позволяет вычислить множество значений. Используя эти значения, определяется искомый результат путем вычисления среднего арифметического или диапазон, в котором может находиться нужный результат.

Общая схема метода Монте-Карло.

Допустим, что нам требуется вычислить какую-то неизвестную величину m. Попытаемся придумать такую случайную величину , чтобы M=m. Пусть при этом D=b^2. Рассмотрим N независимых случайных величин ^1,^2,….^N (реализаций), распределения которых совпадают с распределением . Если N достаточно велико, то согласно центральной предельной теореме распределение суммы pN=i будет приблизительно нормальным с параметрами MpN=Nm, DpN=Nb^2.

На основе Центральной предельной теоремы (или если хотите предельной теоремы Муавра-Лапласа) не трудно получить соотношение: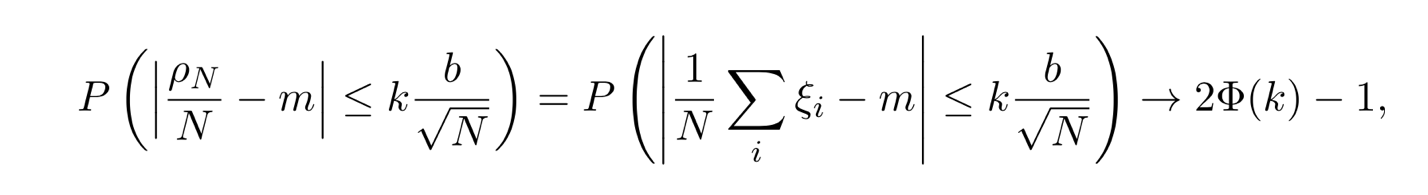


где Ф(х) — функция распределения стандартного нормального распределения.

Это — чрезвычайно важное для метода Монте-Карло соотношение. Оно дает и метод расчета m, и оценку погрешности.

Найдем N значений случайной величины . Из указанного соотношения видно, что среднее арифметическое этих значений будет приближенно равно m. С вероятностью близкой к (2Ф(К)-1) ошибка такого приближения не превосходит величины. ошибка стремится к нулю с ростом N.

В зависимости от целей последнее соотношение используется по-разному:
Если взять k=3, то получим так называемое «правило 3»: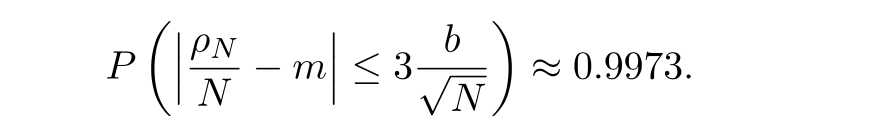

1. 
   Если требуется конкретный уровень надежности вычислений ,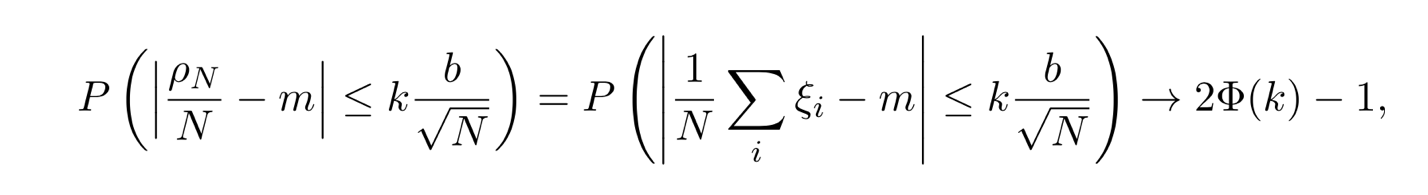
   

Точность вычислений

Как видно из приведенных выше соотношений, точность вычислений зависит от параметра N и величины b – среднеквадратичного отклонения случайной величины .

Указать важность именно второго параметра b.

Рассмотрим вычисление определенного интеграла.

Вычисление определенного интеграла эквивалентно вычислению площадей, что дает интуитивно понятный алгоритм вычисления интеграла. Рассмотрим более эффективный метод. Вместо равномерно распределенной случайной величины в этом методе можно использовать практически любую случайную величину, заданную на том же интервале.

Вычислим интеграл: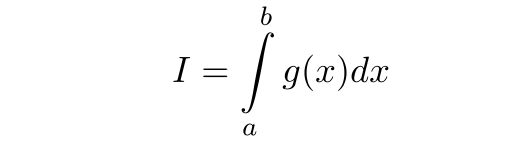


Выберем произвольную случайную величину  с плотностью распределения p(x), определенной на интервале (a,b). И рассмотрим случайную величину



Математическое ожидание последней случайной величины равно: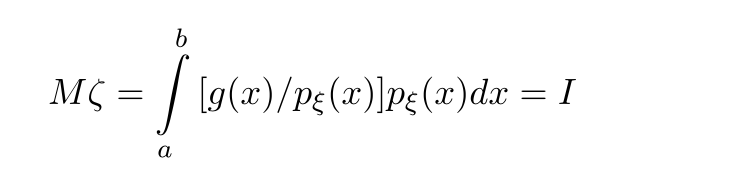


Таким образом: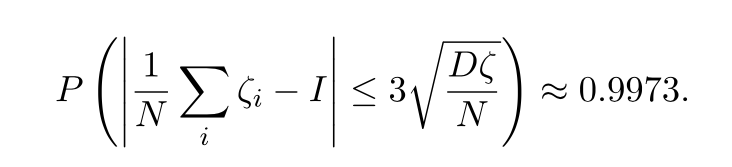


Последнее соотношение если выбрать N значений ^1, ^2,….. ^N, то при достаточно большом N: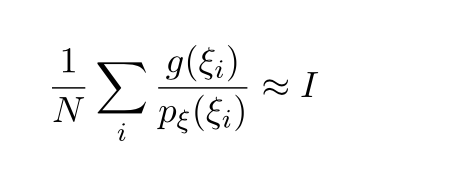



Таким образом, для вычисления интеграла, можно использовать практически любую случайную величину . Но дисперсия D , а вместе с ней и оценка точности, зависит от того какую случайную величину  взять для проведения расчетов.

D  будет иметь минимальное значение, когда p(x) пропорционально |g(x)|. Выбрать такое значение p(x) в общем случае очень сложно (сложность эквивалентна сложности решаемой задачи), но руководствоваться этим соображением стоит, т.е. выбирать распределение вероятностей по форме схожее с модулем интегрируемой функции.

Выберем произвольную случайную величину  с плотностью распределения p(x) , определенной на интервале (a,b). Рассмотрим случайную величину =g()/p().

Математическое ожидание последней случайной величины равно: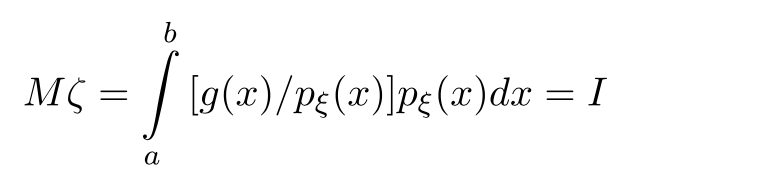



Таким образом: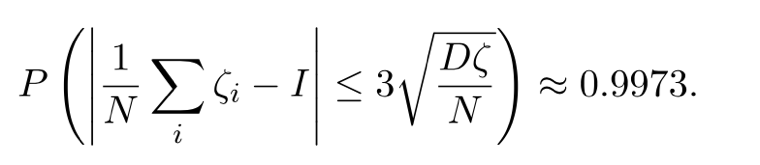



Последнее соотношение означает, что если выбрать N значений ^1, ^2…. ^N, то при достаточно большом соотношении: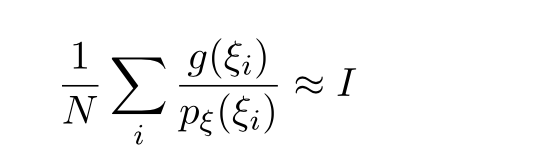



Для вычисления интеграла, можно использовать любую случайную величину . Но дисперсия D, а вместе с ней и оценка точности, зависит от того какую случайную величину  взять для проведения расчетов.

D будет иметь минимальное значение, когда p(x) пропорционально |g(x)|. Выбрать такое значение p(x) в общем случае очень сложно (сложность эквивалентна сложности решаемой задачи), но руководствоваться этим соображением стоит, т.е. выбирать распределение вероятностей по форме схожее с модулем интегрируемой функции.

Численный пример

Численный пример: a=0; b=pi/2; g(x) = cos(x).

Вычислим значение интеграла с применением двух различных случайных величин.

В первом случае используем равномерно распределенную случайную величину на [a,b], т.е. 

p(x)=2/pi.

Во втором случае используем случайную величину с линейной плотностью на [a,b], т.е. p.

График, функций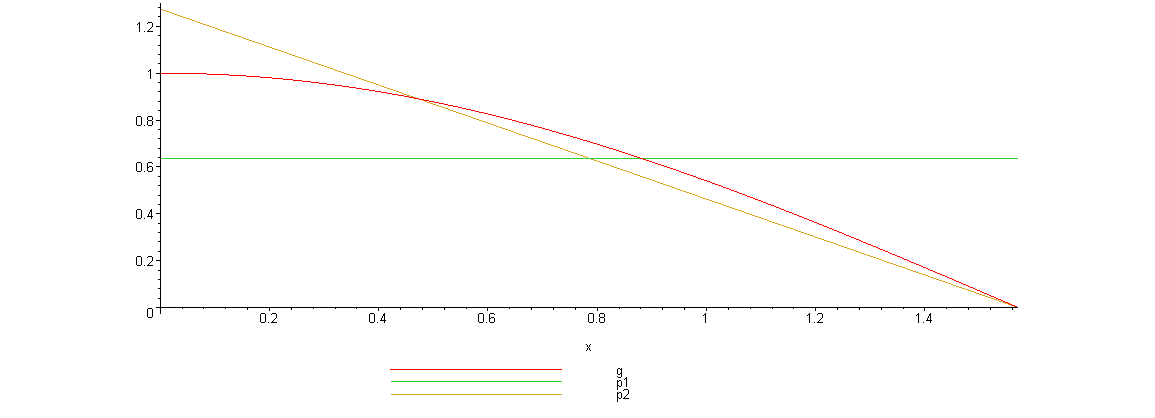

Нетрудно увидеть, что линейная плотность лучше соответствует функции g(x).

Точное значение интеграла легко вычислить аналитически, оно равно 1.

Результаты одного моделирования при N = 10:

Для равномерно распределенной случайной величины: I=1,2166.

Для случайной величины с линейной плотностью распределения: I=0,97641.

В первом случае относительная погрешность более 21%, а во втором 2.35%. Точность  в первом случае равна 0.459, а во втором – 0.123.

Думаю, данный модельный пример показывает важность выбора случайной величины в методе Монте-Карло. Выбрав, правильную случайную величину, можно получить более высокую точность вычислений, при меньшем числе итераций.

Конечно, так не вычисляют одномерные интегралы, для этого есть более точные квадратурные формулы. Но ситуация меняется при переходе к многомерным интегралам, т.к. квадратурные формулы становятся громоздкими и сложными, а метод Монте-Карло применяется лишь с небольшими изменениями.

Количество итераций и генераторы случайных чисел

Не трудно увидеть, что точность вычислений зависит от количества N случайных величин включенных в сумму. Причем, для увеличения точности вычислений в 10 раз нужно увеличить N в 100 раз.

При решении некоторых задач для получения приемлемой точности оценки требуется брать очень большое число N. А учитывая, что метод зачастую работает очень быстро, то реализовать последнее при современных вычислительных возможностях совсем не сложно. И возникает соблазн просто увеличить число N.

Если в качестве источника случайности используется некоторое физическое явление (физический датчик случайных чисел), то все работает отлично.

Часто для вычислений по методу Монте-Карло применяют датчики псевдослучайных чисел. Главная особенность таких генераторов – наличие некоторого периода.

Метод Монте-Карло можно использовать при значениях N не превышающих (лучше много меньших) период вашего генератора псевдослучайных чисел. Последний факт вытекает из условия независимости случайных величин, используемых при моделировании.

При проведении больших расчетов нужно убедиться, что свойства генератора случайных чисел позволяют вам провести эти расчеты. В стандартных генераторах случайных чисел (в большинстве языков программирования) период чаще всего не превосходит 2 в степени разрядности операционной системы, а то и еще меньше. При использовании таких генераторов нужно быть чрезвычайно осторожным. Лучше изучить рекомендации Д. Кнута, и построить свой генератор, имеющий наперед известный и достаточно большой период.

Метод Монте-Карло в информационной безопасности

Постановка задачи и игровой подход

Для поиска наиболее оптимального набора средств защиты компьютерной системы можно провести математическую игру двух сторон, одной из которых является система защиты компьютерной̆ информации (I игрок – администратор), а с другой – возможные атаки хакеров (II игрок – злоумышленник). Один из подходов, моделирующий игру хакера и администратора безопасности, основан на теории позиционных игр.

Позиционная игра — это последовательная многоходовая игра, которая состоит в последовательном переходе из одного состояния (позиции) в другое состояние (позицию) путём выбора игроками одного из возможных действий в соответствии с правилами игры. Позиционные игры описываются с помощью дерева игры. На рис. 1 представлено дерево двухходовой позиционной игры. Каждая вершина дерева – это позиции игры, ход из одной позиции игры в другую позицию задаётся дугой. Начальной позиции игры соответствует корень дерева 𝑅, конечным позициям – листья, из них ходы игроками уже не совершаются. Каждому листу𝑐_𝑖𝑗 (𝑖=1,...,𝑀;𝑗=1,...,𝐾) приписывается выигрыш.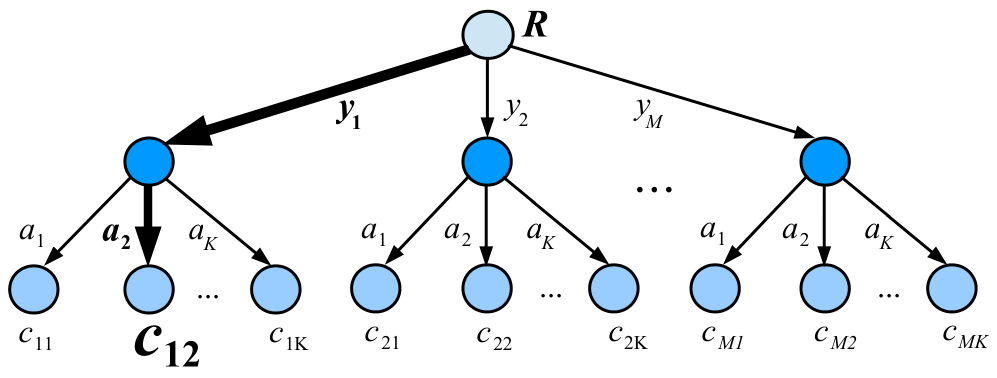


Рис.1 Дерево двухходовой игры хакера и администратора безопасности

Пусть злоумышленник (игрок II) обладает 𝐾 стратегиями атаки на компьютерную систему 𝑎₁,𝑎₂,...,𝑎_𝐾,каждая такая стратегия𝑎_𝑗 (𝑗=1,...,𝐾)–это𝑗-я угроза, способная нарушить работу компьютерной системы. Каждому способу атаки 𝑎_𝑗 (𝑗 = 1, ..., 𝐾 ) соответствует ущерб 𝑙_𝑗 , который терпит администратор в случае успешного осуществления этой 𝑗-ой атаки. Администратор безопасности (игрок I) пусть располагает 𝑆 средствами защиты 𝑑₁,𝑑₂,...,𝑑_𝑆, каждое из которых обладает соответствующей ценой 𝑔₁, 𝑔₂, ..., 𝑔_𝑆 и эффективностью за- щиты 𝑒_𝑖 = (𝑒_𝑖1 , 𝑒_𝑖2 , ..., 𝑒_𝑖𝐾 ) (𝑖 = 1, ..., 𝑆 ), где 𝑒_𝑖𝑗 – эффективность 𝑖-го средства защиты по нейтрализации 𝑗-ой угрозы.

Стратегии администратора — это кортежи

𝑦_𝑖 = (𝑧_𝑖1,𝑧_𝑖2,...,𝑧_𝑖𝑆)

где 𝑧_𝑖𝑗 = 1, если задействован способ защиты 𝑑_𝑗 и 𝑧_𝑖𝑗 = 0 – в противном случае. Имея 𝑆 средств защиты 𝑑_𝑘 (𝑘 = 1, ..., 𝑆), администратор может составить 𝑀 = 2^𝑆 − 1 стратегий 𝑦_𝑖 (𝑖 = 1, ..., 𝑀 ), из которых мы исключили кортеж (0, 0, ..., 0), поскольку он представляет полное бездействие администратора.

Ходом администратора является выборка из способов обеспечения защиты информационной системы (разных наборов средств защиты), т. е. выбор стратегии 𝑦_𝑖, а ходом злоумышленника — применение способа атаки 𝑎_𝑗 на компьютерную систему.

Составим платёжную матрицу 𝐶, элементами 𝑐_𝑖𝑗 которой являются потери администратора в том случае, когда он использовал стратегию 𝑦_𝑖 (𝑖 = 1, ..., 𝑀), а хакер осуществил атаку 𝑎_𝑗 (𝑗 = 1, ..., 𝐾). На дереве игры элементы платёжной матрицы представлены листьями.

Элементы платёжной матрицы вычисляются с помощью формулы:

𝑐_𝑖𝑗 =𝑅(𝑦_𝑖,𝑎_𝑗)+𝐺_𝑖

где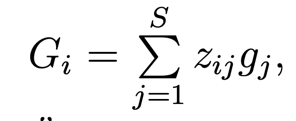


𝑖-той стратегии 𝑦_𝑖;


— остаточный риск атаки 𝑎_𝑗 при использовании


стратегии 𝑦_𝑖, т. е. возможный ущерб, помноженный на вероятность того, что используемые средства защиты окажутся неэффективны.
Путь от корня 𝑅 к листу 𝑐_𝑖𝑗 является партией игры с исходом игры

𝐹(𝑦_𝑖,𝑎_𝑗) = 𝑐_𝑖𝑗 изображён пример партии, в которой администратор избрал стратегию 𝑦₁, а злоумышленник – атаку 𝑎₂ .

Процесс игры состоит в том, что администратор выбирает стратегию защиты 𝑦_𝑖, злоумышленник выбирает способ атаки 𝑎_𝑗, после чего вычисляется исход партии, заключающийся в том, что администратор терпит ущерб равный 𝑐_𝑖𝑗.

Нанесение хакером ущерба обычно является скорее следствием его действий, а не самой целью. В действительности при атаке он может преследовать какие-то свои цели, порой известные лишь ему.

Цель администратора – выбор такой стратегии, которая сводит потери от атак к минимуму, авторы на его стороне, и поэтому цели атакующих хакеров в расчёт не принимаются. В силу этого можно считать, что хакер увлечён желанием нанести как можно больший ущерб атакуемой компьютерной системе. При таком предположении выигрыш хакера будет равен проигрышу администратора безопасности 𝑐_𝑖𝑗.



В качестве стратегий администратора безопасности будем понимать строки 𝑦_𝑖 (𝑖 = 1, ..., 𝑀 ) платёжной матрицы, а в качестве стратегий хакера – её столбцы 𝑎_𝑗 (𝑗 = 1, ..., 𝐾 ) (табл. 1). Перед своим ходом игроки не знают о ходах друг друга. Для проведения на компьютере игры 𝐶 надо также знать результаты игры при каждой паре стратегий 𝑦_𝑖 и 𝑎_𝑗.

Администратор безопасности стремится выбрать такую стратегию, которая позволит ему свести к минимуму наносимый компьютерной системе ущерб от реализации тех или иных угроз. Поставим в соответствие каждой 𝑖-ой стратегии администратора число 𝑊_𝑖(𝐶), вычисляемое с помощью платёжной матрицы 𝐶. Критерий выбора оптимальной стратегии для администратора состоит в том, чтобы взять 𝑊 = min 𝑊_𝑖(𝐶). Тогда оптимальной будет такая стратегия 𝑦_𝑖0, для 𝑖 которой𝑊_𝑖0(𝐶)=𝑊. Будем считать, что администратор не имеет никакой информации о том, какую стратегию (способы атаки) выберет злоумышленник, тогда вероятности атак можно считать одинаковыми и равными 1/𝐾. В таком случае можно воспользоваться критерием недостаточного основания Лапласа, для которого берём: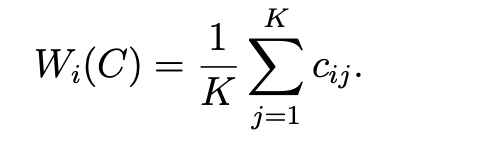



Использование критерия недостаточного основания Лапласа оправдано, если минимизация риска проигрыша представляется менее существенным фактором принятия решения, чем максимизация среднего выигрыша. Администратор при необходимости может применить и другие критерии к подбору оптимального набора средств защиты.


Нахождение оптимальной стратегии администратора безопасности методом Монте-Карло

С увеличением числа 𝑆 средств защиты расчёт и количество 𝑀 = 2^𝑆 − 1 вариантов возможных стратегий защиты компьютерной системы. В результате общее количество возможных партий игры администратора безопасности со злоумышленником можно вычислить по формуле:

𝐴 = 𝐾𝑀 = 𝐾(2^𝑆 − 1).

Например, если возьмём число возможных атак хакера 𝐾 = 10000, число средств защиты администратора 𝑆 = 20, то число возможных стратегий администратора 𝑀 = 1048575 и количество возможных партий игры будет равно 𝐴 = 10485750000.

Для нахождения оптимальной стратегии администратора нужно вычислить по формуле (1) все 𝑊_𝑖(𝐶) для 𝑖 = 1,...,𝑀. Для этого потребуется провести минимум 𝐴 сложений, а в приведённом выше примере это более 10 миллиардов сложений. Данный способ расчёта требует больших затрат на вычислительные ресурсы и уже при данных здесь значениях 𝐾 и 𝑆 оптимальная стратегия администратора может вычисляться продолжительное время. Если ещё в несколько раз увеличить значения 𝐾 и 𝑆, то невозможно будет данным способом найти 𝑊 за разумное время даже с использованием вычислительных машин.

Исходя из этого, актуально нахождение решения рассматриваемой игры методами, которые менее затратны на вычислительные ресурсы. При исследовании сложных систем, подверженных случайным воздействиям, можно использовать имитационное моделирование, которое представляет собой численный метод проведения на ЭВМ вычислительных экспериментов с математической моделью. Результаты поведения рассматриваемой системы, полученные при воспроизведении на имитационной модели, являются случайными реализациями. Для нахождения объективного и устойчивого решения требуется многократное нахождение различных решений с последующей статистической обработкой полученных данных. В настоящее время при имитационном моделировании случайных процессов очень широко используется метод статистических испытаний Монте-Карло.

Для приблизительного вычисления значений 𝑊_𝑖(𝐶), определяемых в (1), можно для каждой стратегии администратора 𝑦_𝑖 (𝑖 = 1, ..., 𝑀 ) провести по 𝑁_𝑦𝑖 симуляций (с выбранными случайным образом атаками), после чего для получившихся результатов расчёта убытков (𝑥_𝑦𝑖1, 𝑥_𝑦𝑖2, ..., 𝑥_𝑦𝑖𝑛, ..., 𝑥_{𝑦𝑖𝑁𝑦𝑖} ) рассчитать их средние значения для каждой стратегии администратора: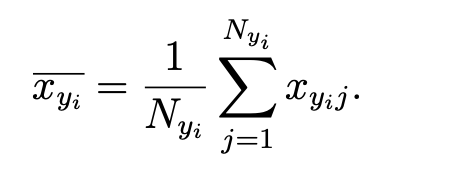


С ростом значения 𝑁_𝑦𝑖 математическое ожидание НЕ 𝑥_{𝑦i будет стремиться к Wi(C):}

M𝑥_𝑦𝑖 → 𝑊_𝑖(𝐶) при 𝑁_𝑦𝑖 → ∞.

Критерием выбора оптимальной стратегии администратора может служить выбор стратегии 𝑦_𝑖0 , для которой:

𝑥_𝑦𝑖0 = min 𝑥_𝑦𝑖 , 𝑖

т. е. стратегии, для которой среднее значение результатов симуляций убытков (ущерба от атак и затрат на средства защиты) минимально. Пусть – общее количество симуляций. Тогда общее количество операций сложения, которые нужно выполнить для расчёта 𝑥_𝑦𝑖 равно 𝑁_𝑦𝑖, а общее количество операций сложения для приблизительного нахождения 𝑊 равно 𝑁. Если 𝑁 < 𝐴, т. е. меньше количества возможных исходов игры, то мы получаем выигрыш по времени.
Оптимизация симуляций

Если количество симуляций для всех стратегий администратора 𝑦_𝑖 установить одинаковым, т. е. все значения 𝑁_𝑦𝑖 (𝑖 = 1,...,𝑀) равными, то данный способ будет неоптимальным.

Например, установив общее количество симуляций 𝑁, на шаге 𝑛 гораздо лучше динамически принимать решение, для какой стратегии проводить очередную симуляцию. Нужно каким-то образом отдавать предпочтения тем стратегиям 𝑦_𝑖, для которых значение 𝑥_𝑦𝑖 на шаге 𝑛 меньше. В таком случае минимальные значения 𝑥_𝑦𝑖 будут быстрее сходиться к своему математическому ожиданию, и мы будем экономить на вычислениях. Мы укажем ниже более эффективный алгоритм выбора стратегий 𝑦_𝑖.
Реализуемый алгоритм USB1

Для минимизации потерь администратора применим алгоритм UCB1 (Upper-Confidence-Bound) к нашей задаче:

Пусть 𝑁 – требуемое количество симуляций и 𝑁 > 𝑀.

1. Шаг 𝑛 = 1. Проведём 𝑀 симуляций, по одной симуляции для каждой стратегии администратора 𝑦_𝑖.

2. Шаг 𝑛, пока 𝑛<𝑁.

На шаге 𝑛 проводим симуляцию 𝑥_𝑦𝑖 для стратегии 𝑦_𝑖, для которой минимальна величина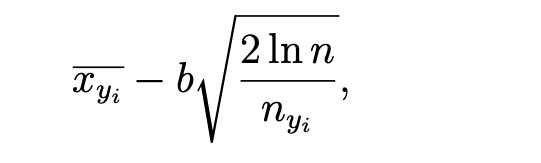



где 𝑥_𝑦𝑖 – средние убытки компьютерной системы при использовании администратором стратегии 𝑦_𝑖 ; 𝑛_𝑦𝑖 – количество уже проведённых симуляций для стратегии 𝑦_𝑖; 𝑛 – номер текущей симуляции;
𝑏 – константа, используемая для установки нужного баланса между шириной и глубиной поиска. Чем она больше, тем чаще будут рассматриваться варианты, для которых средние убытки компьютерной системы не являются минимальными на текущий момент.

На рис. изображены графики радикала при различных значениях 𝑛_𝑦𝑖 . Алгоритмический смысл данного радикала состоит в том, что без него на шаге 𝑛 мы бы каждый раз просто выбирали стратегию с минимальным значением 𝑥_𝑦𝑖. Но так как этот радикал растёт у стратегий, для которых мы не проводим симуляций, то время от времени мы будем проводить симуляции у стратегий, не показывающих минимальный результат на данный момент. Это позволяет сгладить ситуации, когда нам не повезло и для «хороших» стратегий были проведены симуляции с «плохим» результатом.

Описание программного продукта и анализ результатов расчёта

В данной статье мы представляем программный продукт, который по введённым значениям стоимости средств защиты и ущерба от применения атак.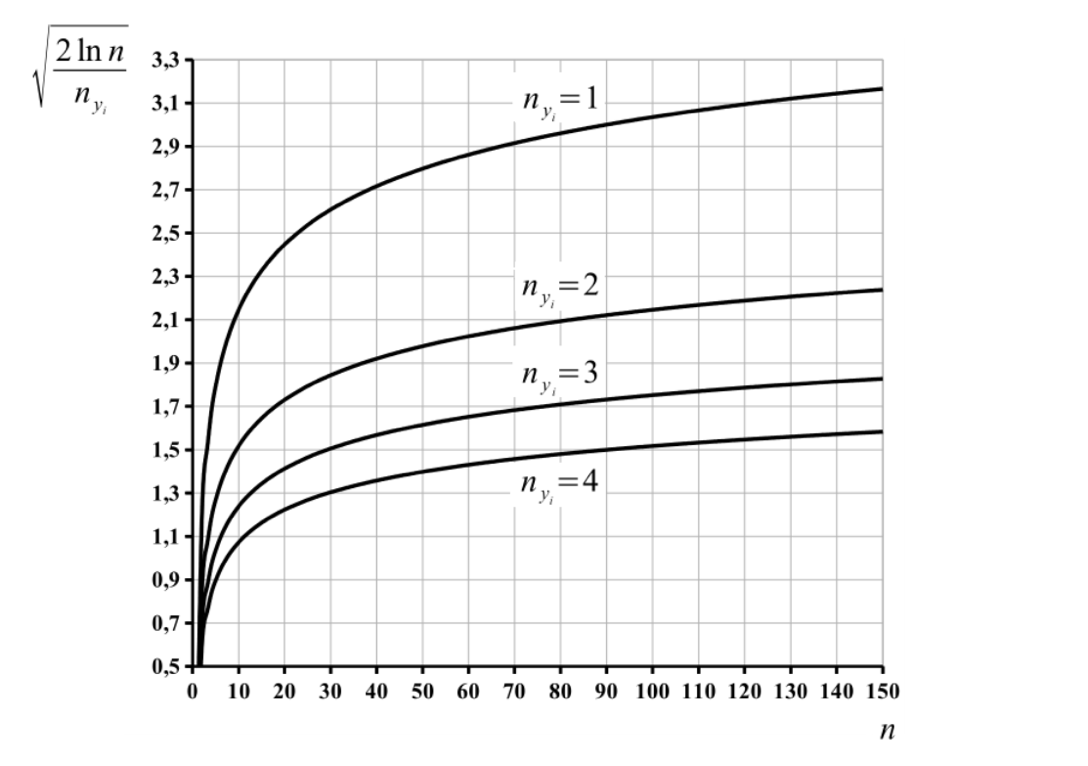



Зависимость величины радикала от номера текущей симуляции 𝑛 для различных значений количества проведенных симуляций 𝑖-ой стратегии администратора.

Позволяет рассчитать оптимальный набор средств защиты компьютерной системы методом Монте-Карло с использованием алгоритма UCB1.

Приложение создавалось в среде разработки IntelliJ IDEA с использованием языка программирования Java. В качестве Фреймворка для автоматической сборки был использован Maven, для разработки графического интерфейса на Java использована библиотека Swing.

На рис. показано главное окно программного приложения, предоставляющее доступ к другим окнам.


Созданное программное приложение на основе набора введённых средств защиты (𝑑₁,𝑑₂,...,𝑑_𝑆) генерирует список из всех возможных стратегий администратора 𝑦_𝑖 (𝑖 = 1, ..., 𝑀 ). Пользователь имеет возможность добавлять новые способы атаки на компьютерную систему и новые средства защиты. В программном приложении можно получить как точное решение задачи, так и решение методом Монте-Карло. Общее количество симуляций является суммой.

Значения поля «Количество симуляций» и количества стратегий администратора.

После проведения необходимых расчётов программное приложение сортирует стратегии администратора в порядке увеличения средних значений затрат на средства защиты и ущерба от атак.

При выборе вида вычисления «Симуляция» программным приложением производятся расчёты для нахождения значений 𝑥_𝑦𝑖 , которые с увеличением количества симуляций приближаются к значениям математического ожидания убытков администратора при выборе соответствующих стратегий. Оптимизация симуляций производилась введением коэффициента смены стратегий (КСС), который является значением 𝑏 из формулы. Этот коэффициент отвечает за то, насколько часто алгоритм будет проводить симуляции для стратегий, у которых на текущей момент убытки не принимают минимального значения.

На рис. 4 показаны результаты работы программного приложения при количестве симуляций 50000 и 𝐾𝐶𝐶 = 5000. В таблицу с лучшим результатом выводится три стратегии с наименьшими средними убытками и с наибольшим количеством симуляций (𝑁_𝑦𝑖).

Программное приложение было запущено на случайно сгенерированных данных с абстрактными способами атаки и методами защиты. На данных малого размера расчёт оптимальных стратегий администратора по методу Монте-Карло существенно проигрывает точному расчёту. Но интерес представляют ситуации, когда количество методов защиты и способов атаки являются большими числами, причём количество способов атак много больше возможных стратегий администратора. На таких данных алгоритм может иметь большое преимущество перед точным расчётом.

Было произведено моделирование на основе случайных данных, когда количество методов защиты равно 7, а способов атак 10 000. Программное приложение было запущено по несколько раз на количестве симуляций 100, 500, 1000, 5000 и 50 000. При малом числе симуляций полученный методом Монте- Карло результат отличался от точных расчётов. На 5000 симуляциях почти во всех случаях программное приложение точно находило одну из двух лучших стратегии, и она была на первом месте в таблице «Лучший результат». На 50000 симуляциях программное приложение всегда точно определяло две лучшие стратегии в правильном порядке.

На 50000 симуляций потребовалось провести 50000 + 2⁷ = 50127, а не 10000(2⁷ − 1) = 1270000 сложений чисел, что составляет 0,04 от исходного количества. Таким образом, удалось добиться существенного выигрыша по времени вычисления оптимального набора средств защиты компьютерной информации.

В рамках данной работы критерием выбора оптимальной стратегии администратора безопасности был использован критерий недостаточного основания Лапласа, предполагающий, что все атаки равновероятны. В случае, когда атаки неравно вероятны и администратору известны их вероятности, можно использовать критерий Байеса.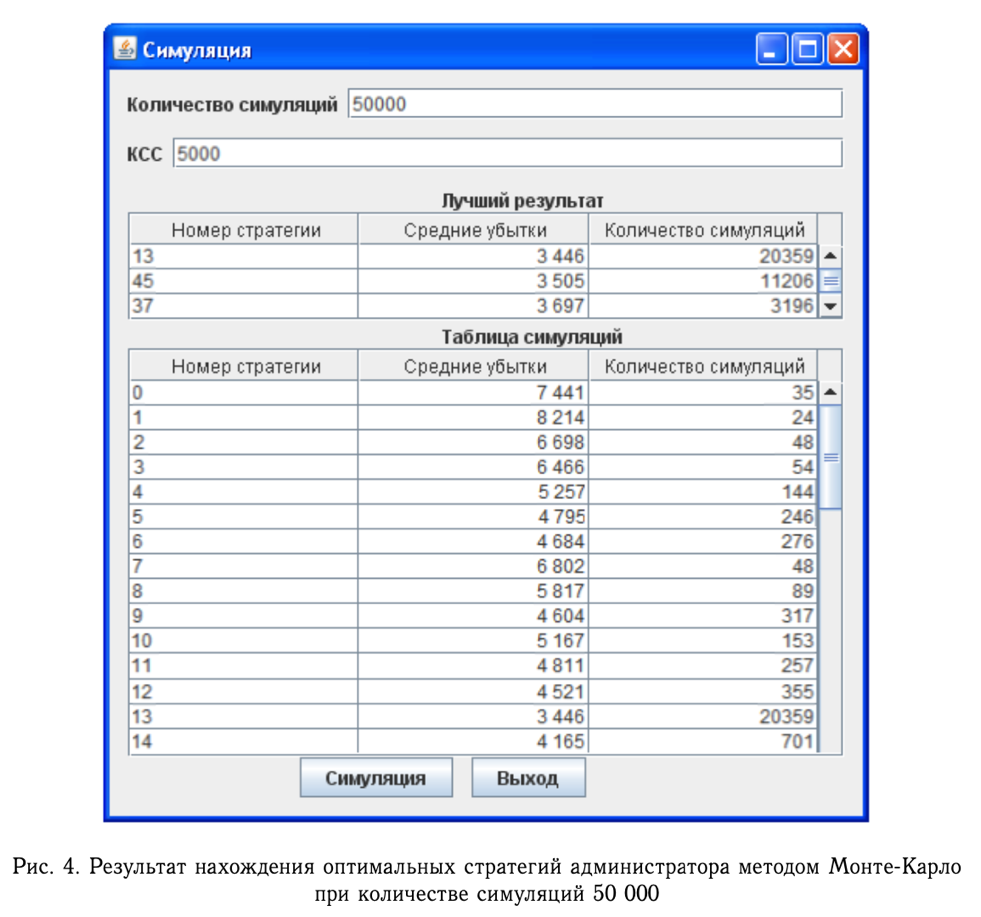






Заключение

Разработанное программное приложение находит оптимальный набор средств защиты компьютерной системы, решая двухходовую позиционную игру администратора безопасности со злоумышленником методом статистических испытаний Монте-Карло.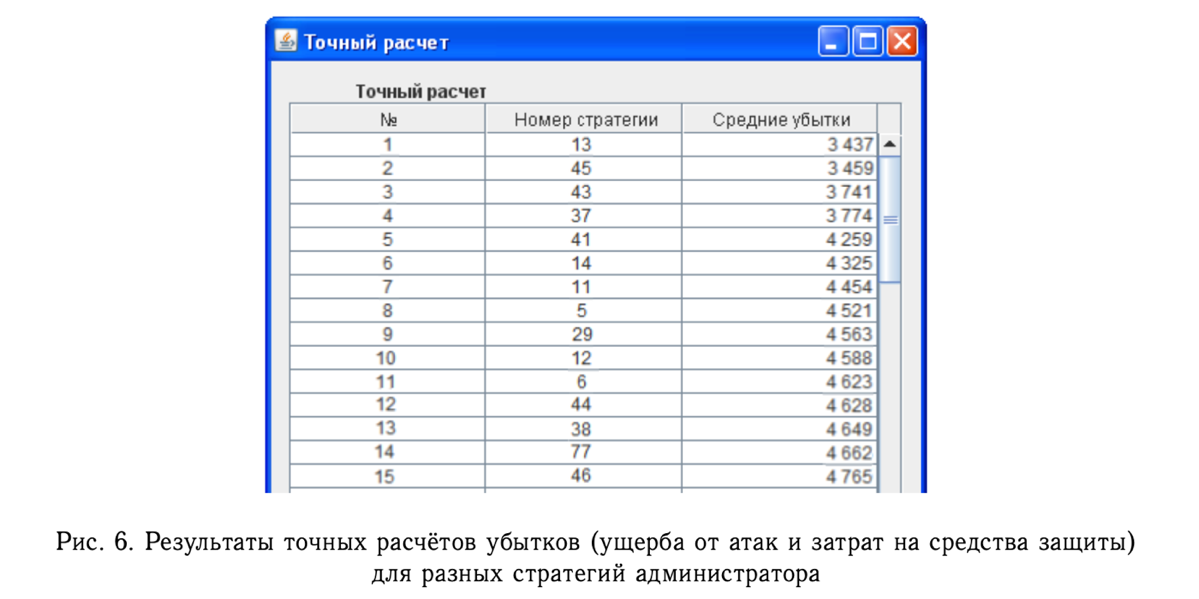



Сравнение полученных результатов с точными расчётами показало, что при огромном количестве возможных атак хакеров и выборе оптимальной стратегии администратора из большого количества средств защиты данный подход позволяет добиться существенного выигрыша по времени нахождения решения.

Список использованной литературы

1. 
   Матричные игры / Под. ред. Н.Н. Воробьёва. М. : ФМ, 1961. 280 с.
   
2. 
   Гуц А.К., Вахний Т.В. Теория игр и защита компьютерных систем: учебное пособие
   
3. 
   Вахний Т.В., Гуц А.К. Теоретико-игровой подход к выбору оптимальных стратегий
   
4. 
   Вахний Т.В., Гуц А.К., Константинов В.В. Программное приложение для выбора оптимального набора средств защиты компьютерной информации на основе теории
   
5. 
   Вахний Т.В., Гуц А.К., Новиков Н.Ю. Матрично-игровая программа с выбором критерия для определения оптимального набора средств защиты компьютерной системы // Математические структуры и моделирование. 2016. No 2(38). С. 103–115.
   
6. 
   Вахний Т.В., Гуц А.К., Бондарь С.С. Учёт вероятностей хакерских атак в игровом подходе к подбору программных средств защиты компьютерной информации
   
7. 
   Шевченко Д.В. Методы принятия управленческих решений: задания и методические указания для выполнения расчётно-графической работы. Казань : Познание,