Критерий Лапласа Колесниченко (1). Критерий Лапласа
 Скачать 35.09 Kb. Скачать 35.09 Kb.
|
|
Критерий Лапласа. Этот критерий опирается на «принцип недостаточного основания» Лапласа, согласно которому все состояния «природы» Si, i = 1,n полагаются равновероятными. В соответствии с этим принципом каждому состоянию Si, ставится вероятность qi определяемая по формуле При этом исходной может рассматриваться задача принятия решения в условиях риска, когда выбирается действие Rj, дающее наибольший ожидаемый выигрыш. Для принятия решения для каждого действия Rj вычисляют среднее арифметическое значение выигрыша: Среди Mj(R) выбирают максимальное значение, которое будет соответствовать оптимальной стратегии Rj. Другими словами, находится действие Rj , соответствующее Если в исходной задаче матрица возможных результатов представлена матрицей рисков ||rji||, то критерий Лапласа принимает следующий вид: Пример 4. Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги не известен, но ожидается (прогнозируется), что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги. Ниже приводится таблица, определяющая возможные прогнозируемые затраты на развитие провозных возможностей: Таблица 10- прогнозируемые затраты на развитие провозных возможностей
Необходимо выбрать оптимальную стратегию. Решение: Согласно условию задачи, имеются четыре варианта спроса на транспортные услуги, что равнозначно наличию четырех состояний «природы»: S1, S2, S3, S4. Известны также четыре стратегии развития провозных возможностей транспортного предприятия: R1, R2, R3, R4 Затраты на развитие провозных возможностей при каждой паре Si и Rj заданы следующей матрицей (таблицей): 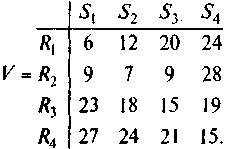 Рисунок 4-матрица для принятия решения Принцип Лапласа предполагает, что S1, S2, S3, S4 равновероятны. Следовательно, P{S = Si }= 1/n= 1/4 = 0,25, i = 1, 2, 3, 4 и ожидаемые затраты при различных действиях R1, R2, R3, R4 составляют: 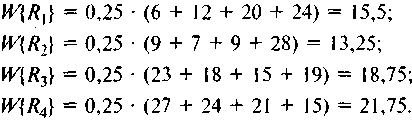 Таким образом, наилучшей стратегией развития провозных возможностей в соответствии с критерием Лапласа будет R2. Критерий Лапласа основан на принципе недостаточного обоснования. Поскольку в рамках информационного подхода в ситуации неопределенности вероятности состояний неизвестны, то нет оснований утверждать, что они различны. Поэтому можно допустить, что они одинаковы. По критерию Лапласа в качестве оценки альтернативы используется средний выигрыш: 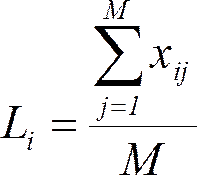 Оптимальной является альтернатива с максимальным средним выигрышем: Х* = Хk, Lk = max(Li), i = 1..N Пример применения критерия Лапласа Для условий примера (табл. 2) использование критерия Лапласа будет выглядеть следующим образом: 1. Найти среднее арифметическое значение исходов по каждому проекту. Оно является оценкой альтернативы по критерию Лапласа: L1 = (x11+x12+x13)/3 = (45+25+50)/3 = 40 L2 = (x21+x22+x23)/3 = (20+60+25)/3 = 35 2. Сравнить рассчитанные величины и найти альтернативу с максимальным значением критерия: 40 > 35 => L1 > L2 => X* = X1 По критерию Лапласа оптимальным является проект Х1, у которого наибольшая средняя прибыль. Среднее значение является достаточно популярной мерой в условиях неопределенности и даже риска, однако оно не учитывает разброс результатов относительно этого значения. Так, например, альтернативы А{400; 600} и В{0; 1000} являются эквивалентными по критерию Лапласа (LA = LB = 500), однако альтернатива В более "рискованна", так как предполагает возможность при плохом стечении обстоятельств не получить ничего. | |||||||||||||||||||||||||||||
