Шпоргалка математика. 2. Пусть имеем два ряда с положительными членами (2) и (3). Теорема 1
 Скачать 326.99 Kb. Скачать 326.99 Kb.
|
| 18. Вычисление тройного интеграла Предположим, что пространственная область V, ограниченная замкнутой поверхностью S, обладает следующими свойствами: 1. Всякая прямая, параллельная оси OZ, проведенная через внутреннюю точку области V , пересекает поверхность S в двух точках. 2. Вся область V проектируется на плоскость ХОУ в правильную область D. 3. Всякая часть области V, отсеченная плоскостью, параллельной и любой из координатных плоскостей, также обладает свойствами 1, 2. Область V, обладающую указанными свойствами, будем называть правильной трехмерной областью. Пример – эллипсоид, тетраэдр. Пусть поверхность, ограничивающая область V снизу, имеет уравнение:  , а сверху – , а сверху – 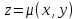 . Пусть область D – проекция области V на плоскость ХОУ – ограниченна линиями: . Пусть область D – проекция области V на плоскость ХОУ – ограниченна линиями: 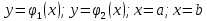 . Введем понятие трехкратного интеграла от функции . Введем понятие трехкратного интеграла от функции 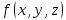 по области V: по области V: 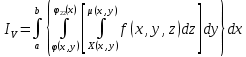 . В результате интегрирования по z в квадратных скобках, получится функция от х и у. Далее вычисляем двойной интеграл по области D . Теорема. Тройной интеграл от . В результате интегрирования по z в квадратных скобках, получится функция от х и у. Далее вычисляем двойной интеграл по области D . Теорема. Тройной интеграл от 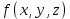 по правильной области равен трехкратному интегралу по этой же области, т.е. по правильной области равен трехкратному интегралу по этой же области, т.е.  . .Свойства тройного интеграла: 1. Если область V разбита на области 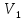 и и 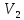 плоскостью, параллельной какой – либо из плоскостей координат, то тройной интеграл по области V равен сумме тройных интегралов по областям плоскостью, параллельной какой – либо из плоскостей координат, то тройной интеграл по области V равен сумме тройных интегралов по областям 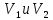 . . 2. Если m и М – наименьшее и наибольшее значение функции 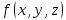 в области V, то в области V, то 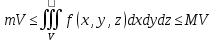 , где V – объем данной области. , где V – объем данной области. 3. 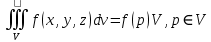 , где V – объем области. , где V – объем области. 4. Если в тройном интеграле положить  . . | 12. Рассмотрим в плоскости XOY замкнутую область D, ограниченную линией L. Пусть в области D задана непрерывная функция  . Разобьем область D на n частей: . Разобьем область D на n частей:  называемых площадками. Через называемых площадками. Через 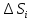 обозначим и площади площадок. В каждой из площадок возьмем точку обозначим и площади площадок. В каждой из площадок возьмем точку 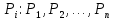 . Обозначим через . Обозначим через  значения функции в выбранных точках и составим сумму произведении вида значения функции в выбранных точках и составим сумму произведении вида 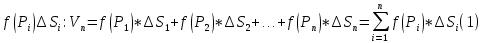 . Эта сумма называется интегральной суммой для функции . Эта сумма называется интегральной суммой для функции 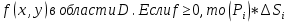 – объем цилиндра, построенного на – объем цилиндра, построенного на 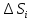 как на основании с высотой как на основании с высотой 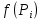 . .Теорема 1. Если 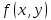 непрерывна в замкнутой области D, то существует предел последовательности (2) интегральных сумм (1), если max диаметр площадок непрерывна в замкнутой области D, то существует предел последовательности (2) интегральных сумм (1), если max диаметр площадок 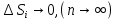 , который не зависит ни от способов разбиения области D, ни от выбора точек , который не зависит ни от способов разбиения области D, ни от выбора точек 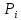 . Этот предел называется двойным интегралом от функции . Этот предел называется двойным интегралом от функции 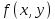 по области D и обозначается: по области D и обозначается: 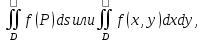 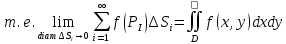 , D – область интегрирования. Если , D – область интегрирования. Если 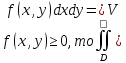 – объему тела, ограниченного поверхностью – объему тела, ограниченного поверхностью 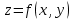 , плоскостью , плоскостью 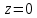 и цилиндрической поверхностью, образующие которой параллельны и цилиндрической поверхностью, образующие которой параллельны 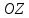 , а направляющей служит граница области D. , а направляющей служит граница области D.Теорема 2. Двойной интеграл от суммы двух функций 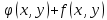 по области D равен сумме двойных интегралов по области D от каждой из функций в отдельности. по области D равен сумме двойных интегралов по области D от каждой из функций в отдельности.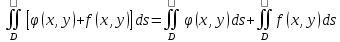 Теорема 3. Постоянный множитель можно вынести за знак двойного интеграла:  Теорема 4. Если область D разбита на две области  без общих внутренних точек и функция. без общих внутренних точек и функция.Теорема 5. (теорема о среднем).  Теорема 6. Если 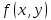 во всех точках области D удовлетворяет неравенствам во всех точках области D удовлетворяет неравенствам 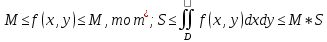 , где S – площадь области D. , где S – площадь области D. | 17. Понятие тройного интеграла Пусть в пространстве задана область V, ограниченная замкнутой поверхностью S. Пусть в области V и на ее границе определена непрерывная функция 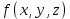 (если (если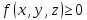 – то можно рассматривать плотность распределения вещества в области V). Разобьем область V на n областей – то можно рассматривать плотность распределения вещества в области V). Разобьем область V на n областей 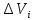 произвольным образом, причем произвольным образом, причем 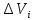 – это и объем этой области. В пределах каждой частичной области – это и объем этой области. В пределах каждой частичной области 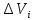 выберем произвольную точку выберем произвольную точку 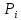 и составим интегральную сумму и составим интегральную сумму 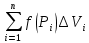 . Перейдем к пределу, т.е. . Перейдем к пределу, т.е. 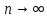 , чтобы и , чтобы и 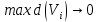 , тогда для непрерывной функции , тогда для непрерывной функции 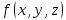 существует предел интегральных сумм, который не зависит ни от способа разбиения области, ни от выбора точек существует предел интегральных сумм, который не зависит ни от способа разбиения области, ни от выбора точек 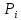 Это предел обозначается символом Это предел обозначается символом 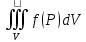 и называется тройным интегралом, т.е. и называется тройным интегралом, т.е.  . Если считать . Если считать 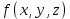 – объемной плотностью распределения вещества в области V, то тройной интеграл даст массу вещества в области V. – объемной плотностью распределения вещества в области V, то тройной интеграл даст массу вещества в области V.11. Имеется формула Тейлора для функции 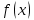 , имеющий производные до , имеющий производные до 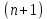 включительно, в окрестности точки включительно, в окрестности точки 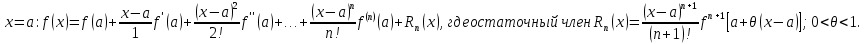 Если Если 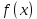 имеет производные всех порядков в окрестности точки имеет производные всех порядков в окрестности точки 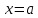 , то в формуле Тейлора число n можно брать сколь угодно большим. Допустим, что , то в формуле Тейлора число n можно брать сколь угодно большим. Допустим, что 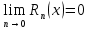 , тогда, переходя в формуле Тейлора к пределу при , тогда, переходя в формуле Тейлора к пределу при 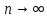 , получим справа бесконечный ряд, Тейлора: , получим справа бесконечный ряд, Тейлора: 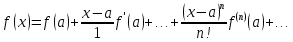 . Если в формуле ряда Тейлора положить . Если в формуле ряда Тейлора положить 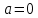 , то получим ряд Маклорена: , то получим ряд Маклорена:  . Для каждой элементарной функции существуют . Для каждой элементарной функции существуют 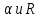 , такие, что в интервале , такие, что в интервале  она разлагается в ряд Тейлора (или Маклорена). она разлагается в ряд Тейлора (или Маклорена). | 16. Пусть в полярной системе координат 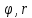 задана такая область D, что каждый луч, проходящий через внутреннюю точку области, пересекает границу области не более чем в двух точках. D ограничена кривыми задана такая область D, что каждый луч, проходящий через внутреннюю точку области, пересекает границу области не более чем в двух точках. D ограничена кривыми 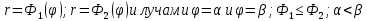 . Такую область называют правильной. . Такую область называют правильной.Пусть в области D задана непрерывная функция 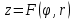 Разобьем D на площадки Разобьем D на площадки 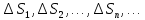 и составим интегральную сумму и составим интегральную сумму  Из теоремы существования двойных интегралов следует, что при 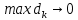 существует предел V интегральной суммы: существует предел V интегральной суммы: 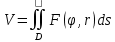 Т.к. предел интегральной суммы не зависит от способа разбиения D, то разобьем D с помощью лучей Т.к. предел интегральной суммы не зависит от способа разбиения D, то разобьем D с помощью лучей 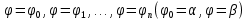 и концентрических окружностей: и концентрических окружностей:  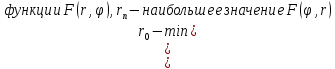 Обозначим через 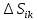 площадку, ограниченную линиями площадку, ограниченную линиями 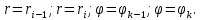 Если площадка 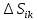 пересекается границей или не лежит в D, то их не учитываем пересекается границей или не лежит в D, то их не учитываем 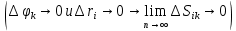 . Интегральная сумма . Интегральная сумма 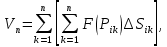 где где 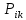 – произвольная точка площадки – произвольная точка площадки 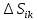 . Найдем площадь . Найдем площадь 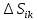 . Она равна разности площадей двух секторов: ощадь . Она равна разности площадей двух секторов: ощадь 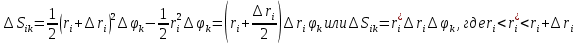 . Тогда интегральная сумма: . Тогда интегральная сумма: 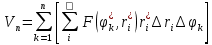 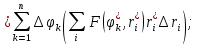  . Предположим, что . Предположим, что 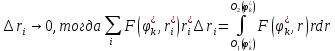 . . Теперь пусть 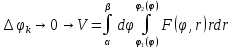 – формула для вычисления двойного интеграла в полярных координатах. Если область D является правильной в полярных координатах, то – формула для вычисления двойного интеграла в полярных координатах. Если область D является правильной в полярных координатах, то 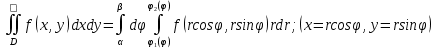 . . | 13. Пусть область D такова, что всякая прямая, параллельна, одной из координатных осей, например, оси 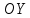 и проходящая через внутреннюю точку области D пересекает границу области в двух точках. Предположим, что область ограничена линиями: и проходящая через внутреннюю точку области D пересекает границу области в двух точках. Предположим, что область ограничена линиями:  причем причем  и функции и функции 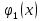 и и 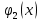 непрерывны на отрезке непрерывны на отрезке 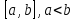 . Такая область называется правильной в направлении оси . Такая область называется правильной в направлении оси 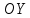 . Аналогично, определяется область, правильная в направлении оси . Аналогично, определяется область, правильная в направлении оси  . Область, правильную как в направлении оси . Область, правильную как в направлении оси  . так и оси . так и оси 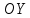 , называют правильной. , называют правильной.Пусть 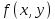 непрерывна в области D. Рассмотрим непрерывна в области D. Рассмотрим 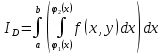 , который будем называть двукратным интегралом от , который будем называть двукратным интегралом от 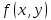 по области D. В этом выражении сначала вычисляется определенный интеграл, стоящий в скобках, при этом считаем, что по области D. В этом выражении сначала вычисляется определенный интеграл, стоящий в скобках, при этом считаем, что 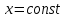 получаем функцию получаем функцию 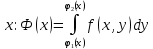 далее вычисляем определенный интеграл далее вычисляем определенный интеграл  , который равен постоянному числу. , который равен постоянному числу.Пусть область D такова, что одна из функций  не может быть задана одним аналитическим выражением на всем участке не может быть задана одним аналитическим выражением на всем участке 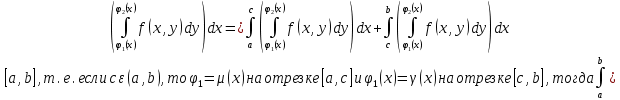 Теорема. Двойной интеграл от непрерывной функции 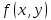 по правильной области D равен двукратному интегралу от этой функции по области D: по правильной области D равен двукратному интегралу от этой функции по области D:  Замечание 1. Пусть правильная в направлении оси OX область D ограниченная линиями 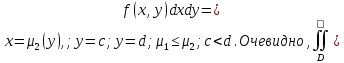 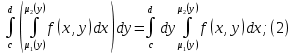 . Для вычисления двойного интеграла его надо представить в виде двукратного. В каждом конкретном случаи надо выбрать формулу (1) или (2) в зависимости от вида области и подынтегральной функции . Для вычисления двойного интеграла его надо представить в виде двукратного. В каждом конкретном случаи надо выбрать формулу (1) или (2) в зависимости от вида области и подынтегральной функции 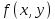 . . |
| 1. Пусть задана бесконечная последовательность чисел 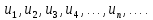 . Выражение . Выражение 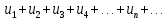 (1) называется числовым рядом. Числа (1) называется числовым рядом. Числа 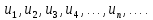 , называются членами ряда. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда: , называются членами ряда. Сумма конечного числа n первых членов ряда называется n-ой частичной суммой ряда: 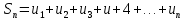 Рассмотрим частичные суммы: Рассмотрим частичные суммы:  . Если существует конечный предел . Если существует конечный предел 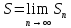 , то его называют суммой ряда (1) и говорят, что ряд сходится. Если , то его называют суммой ряда (1) и говорят, что ряд сходится. Если 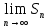 не существует, то ряд расходится и суммы не имеет. не существует, то ряд расходится и суммы не имеет. Теорема 1. Если сходится ряд, полученный из данного ряда (1) отбрасыванием нескольких его членов, то сходится и сам данный ряд. Обратно, если сходится данный ряд, то сходится и ряд, полученный из данного ряда отбрасыванием нескольких членов. Теорема 2. Если ряд 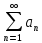 сходится и его сумма равна S, то ряд сходится и его сумма равна S, то ряд 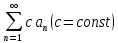 тоже сходится и его сумма =Sc. тоже сходится и его сумма =Sc.Теорема 3. Если ряды 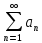 и и 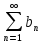 сходятся и их суммы равны соответственно сходятся и их суммы равны соответственно  и и 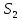 , то ряды , то ряды 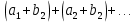 и и  тоже сходятся и их суммы равны тоже сходятся и их суммы равны 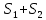 и и 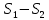 соответственно. соответственно.Теорема. Если ряд сходится, то его n-й член стремится к нулю при неограниченном возрастании n. |
