случайной величины и ее свойства
Непрерывную случайную величину можно задать функцией распределения, однако можно использовать и плотностью распределения. Плотностью распределения вероятностей непрерывной случайной величины Х называют производную от функции распределения: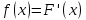 . Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима. . Для описания распределения вероятностей дискретной случайной величины плотность распределения неприменима.
Теорема. Вероятность того, что непрерывная случайная величина Х примет значение, принадлежащее интервалу 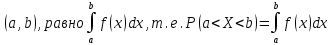
Доказательство: Если известна функция распределения, то 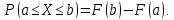 По формуле Ньютона-Лейбница: По формуле Ньютона-Лейбница: 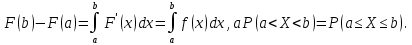 Свойства f(x) Свойства f(x)
1. 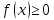 , т.к. , т.к.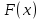 – неубывающая функция, поэтому, – неубывающая функция, поэтому, 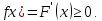
2. 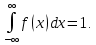 Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение Этот интеграл выражает вероятность события, состоящего в том, что случайная величина примет значение 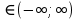 – достоверное событие, поэтому – достоверное событие, поэтому 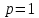 . .
Вероятностный смысл 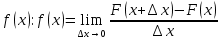 , тогда: , тогда: 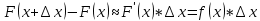 – вероятность того, что случайная величина примет значение – вероятность того, что случайная величина примет значение 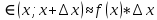 . .
37. Числовые характеристики непрерывных случайных величин
Распространим определение числовых характеристик дискретных случайных величин на величины непрерывные.
Математическое ожидание 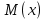 . Пусть Х задана плотностью распределения . Пусть Х задана плотностью распределения 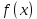 . Допустим, что все возможные значения . Допустим, что все возможные значения 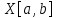 . Разобьем его на n отрезков . Разобьем его на n отрезков 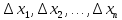 и выберем на каждом произвольную точку и выберем на каждом произвольную точку 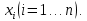 Тогда Тогда 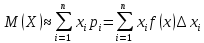 . Переходя к пределу, получим: . Переходя к пределу, получим: 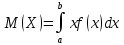 . Если возможные значения случайной величины принадлежат R, то . Если возможные значения случайной величины принадлежат R, то 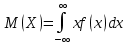 , предполагаем, что этот интеграл сходится. Дисперсия дискретной случайной величины: , предполагаем, что этот интеграл сходится. Дисперсия дискретной случайной величины: 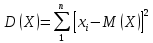 . Поступим аналогично: . Поступим аналогично: 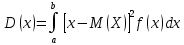 . Если . Если 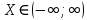 , то , то 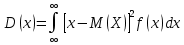 . Более удобная формула: . Более удобная формула: 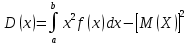 . .
Аналогично: 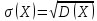 – среднее квадратическое отклонение непрерывной случайной величины. Свойства – среднее квадратическое отклонение непрерывной случайной величины. Свойства 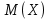 и и 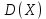 сохраняются для непрерывных случайных величин. сохраняются для непрерывных случайных величин.
38. Нормальное распределение
Нормальным распределением называется распределение вероятностей непрерывных случайных величин, которые описываются плотностью распределения 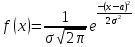 . Нормальное распределения определяются параметрами а и . Покажем, что . Нормальное распределения определяются параметрами а и . Покажем, что 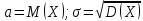 . .
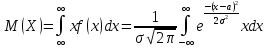 . Введем: . Введем: 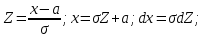
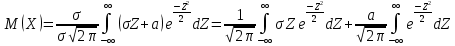 . Первое слагаемое равно нулю, т.к. функция нечетная, пределы интегрирования симметричны относительно начала координат, . Первое слагаемое равно нулю, т.к. функция нечетная, пределы интегрирования симметричны относительно начала координат, 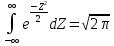 (это – интеграл Пуассона). Таким образом, (это – интеграл Пуассона). Таким образом, 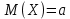 . .
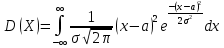 . Пусть . Пусть 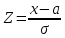 тогда тогда 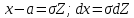 . .
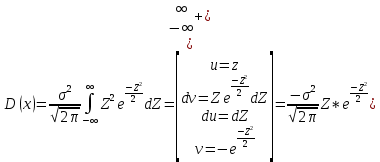 , тогда , тогда 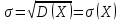
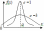
|
39. Вероятности попадания в заданный интервал и заданного отклонения для нормальной случайной величины.
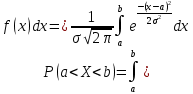 . Пусть . Пусть 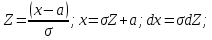 . .
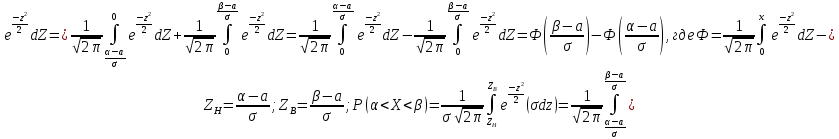
функция Лапласа.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Вычисление вероятности заданного отклонения
Часто требуется найти вероятность того, что отклонение нормально распределенной случайной величины Х от математического ожидания по модулю меньше данного 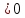 . .
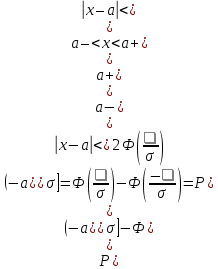 Если Если 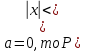
Правило 3x сигм: если 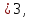 то то 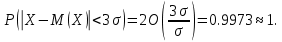
|
40. Задачи математической статистики. Вариационный ряд
Первая задача статистики – указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или экспериментов.
Вторая задача – разработать методы анализа статистических данных в зависимости от целей исследования:
а) оценка неизвестной вероятности события, известной функции распределения, параметров распределения, вид которого известен и т.д.
б) проверка статистических гипотез о виде неизвестного распределения или о величине параметров распределения, вид которого известен.
Для исследования какого-либо признака из генеральной совокупности (всех объектов) извлекают выборку – случайно отображенные объекты.
Вариационный ряд
Рассмотрим пример. Токарь изготавливал в течение 10 дней следующее количество деталей: 5,6,5,7,7,7,8,5,6,5. Ранжируем эту выборку – разобьем на группы:
5,5,5,5 6,6 7,7,7 8
4 раза 2 раза 3 раза 1 раз.
При ранжировании группы располагаются в порядке возрастания. Значение каждой группы называется вариантой. Число повторений в каждой группе называется частотой варианты. Полученную таблицу называют вариационным рядом.
В общем виде
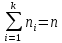 – объем выборки. – объем выборки.
Графическое изображение вариационного ряда – полигон. Для непрерывного признака весь интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько частичных интервалов длиной h и находят для каждого частичного интервала 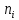 – сумму частот вариант, попавших в i-й интервал. – сумму частот вариант, попавших в i-й интервал.
Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны 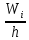 , где , где 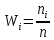 – относительная частота. – относительная частота.
|
41. 42.Точечные оценки
Вариационный ряд характеризует случайную величину, но не в полной мере, поэтому используются характеристики, аналогичные теоретическим – М(х), D(х) и т.д. Эти числовые характеристики подсчитываются на основании выборки и называются точечными оценками (т.к. являются числами). Точечной оценкой характеристики называется некоторая функция * результатов наблюдений, значение которой принимают за приближение этой характеристики: 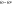 . Качество точечной оценки определяется характеристиками: . Качество точечной оценки определяется характеристиками:
1. Несмещенность оценки: точечная оценка называется несмещенной, если ее математическое ожидание равно оценивающему параметру: 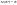 , т.е. совпадает с истинным значением. , т.е. совпадает с истинным значением.
2. Состоятельность: точечная оценка называется состоятельной, если она при 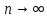 стремится по вероятности к оцениваемому параметру. стремится по вероятности к оцениваемому параметру.
3. Эффективность: точечная оценка считается эффективной, если она имеет (при заданном n) наименьшую дисперсию.
Основные точечные оценки
1. Выборочная средняя: 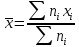 . .
Выборочная средняя 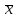 приближается к приближается к 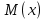 , является несмещенной, состоятельной и эффективной. , является несмещенной, состоятельной и эффективной.
2. Выборочная дисперсия: 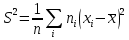 . . 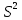 является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию: является состоятельной, но смещенной, поэтому часто используют несмещенную оценку – исправленную выборочную дисперсию: 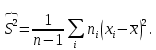
3. Начальные и центральные моменты k-го порядка. Начальный момент k-го порядка: 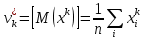 . Центральный момент k-го порядка: . Центральный момент k-го порядка: 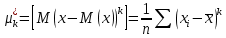
|
43. Интервальные оценки для генеральной средней
При выборке малого объема точечная оценка может сильно отличаться от оцениваемого параметра, поэтому широко используют интервальные оценки. Интервальной называют оценку, которая определяется двумя числами – концами интервала. Доверительной вероятностью (надежностью) называется вероятность , с которой осуществляется неравенство 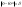 , т.е. , т.е. 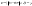 , где * – найденная характеристика параметра . Надежность , где * – найденная характеристика параметра . Надежность  обычно выбирается 0,95; 0,99; 0,999 и т.д. обычно выбирается 0,95; 0,99; 0,999 и т.д.
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Интервальные оценки для генеральной средней с известным . Пусть известно среднее квадратическое отклонение генеральной совокупности с нормальным законом распределения. Требуется оценить неизвестное математическое ожидание, а по выборочной средней 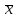 . Будем рассматривать выборочную среднюю . Будем рассматривать выборочную среднюю 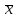 , как случайную величину , как случайную величину 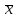 , для которой , для которой 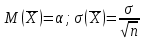
(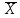 – случайная величина, т.к. – случайная величина, т.к.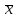 меняется от выборки к выборке). меняется от выборки к выборке).
Тогда по следствию интегральной теоремы Лапласа имеем: 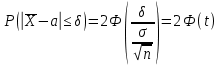 , где , где 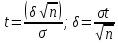 , – точность оценки. Число t определяем по таблице значений функции Лапласа: , – точность оценки. Число t определяем по таблице значений функции Лапласа: 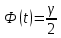 . Получаем: . Получаем: 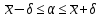 , ,
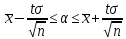 – интервальная оценка для математического ожидания – интервальная оценка для математического ожидания 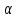
- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Интервальная оценка для генеральной средней с неизвестным . Пусть признак Х генеральной совокупности распределен нормально, причем среднее квадратическое отклонение неизвестно. Требуется оценить неизвестное математическое ожидание а по выборочной средней 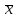 . Для построения интервальной оценки используется статистика . Для построения интервальной оценки используется статистика 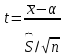 , имеющая распределение Стьюдента с числом степеней свободы , имеющая распределение Стьюдента с числом степеней свободы 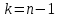 . Получаем: . Получаем: 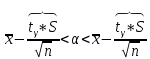 где n – объем выборки, где n – объем выборки, 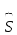 – исправленное среднее квадратическое отклонение, – исправленное среднее квадратическое отклонение, 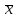 – выборочная средняя, – выборочная средняя, 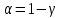 – уровень значимости, – уровень значимости, 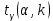 находим по распределению Стьюдента (t – распределение) (для двухсторонней критической области). Точность оценки: находим по распределению Стьюдента (t – распределение) (для двухсторонней критической области). Точность оценки: 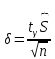 . Можно по таблице приложения 3 Гмурмана. . Можно по таблице приложения 3 Гмурмана.
|
44. Интервальные оценки для генеральной дисперсии, среднего квадратического отклонения и генеральной доли
Пусть из генеральной совокупности, распределенной по нормальному закону 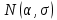 , взята выборка объема n и вычислена исправленная выборочная дисперсия , взята выборка объема n и вычислена исправленная выборочная дисперсия 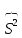 . Требуется определить с надежностью интервальные оценки для . Требуется определить с надежностью интервальные оценки для 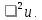
Случайная величина 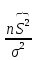 имеет распределение Пирсона имеет распределение Пирсона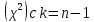 степенями свободы. Имеем: степенями свободы. Имеем: 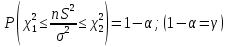 . По таблице . По таблице 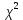 - распределения нужно выбрать такие - распределения нужно выбрать такие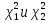 , чтобы площадь, заключенная под графиком плотности распределения , чтобы площадь, заключенная под графиком плотности распределения 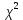 между между 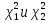 , была равна , была равна 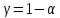 . Обычно: . Обычно: 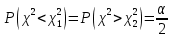 . .
Т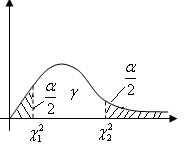 огда: огда: 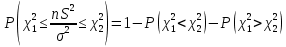 . Поскольку таблица содержит лишь . Поскольку таблица содержит лишь 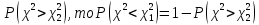 , то тогда из , то тогда из 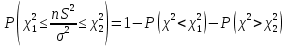
из 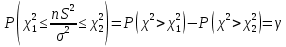 , т.е. , т.е. 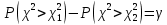 . Эта формула используется при решении обратной задачи – нахождение доверительной вероятности по заданному доверительному интервалу генеральной дисперсии. . Эта формула используется при решении обратной задачи – нахождение доверительной вероятности по заданному доверительному интервалу генеральной дисперсии. 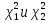 находим из равенств: находим из равенств: 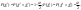 Запишем неравенство из Запишем неравенство из 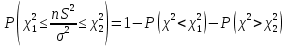 : :
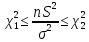 и преобразуем его: и преобразуем его: 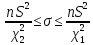 . .
Если 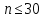 , то доверительный интервал для , то доверительный интервал для  : : 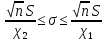 . Если . Если 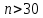 , то , то 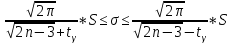 , где , где 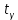 определяется по таблице функции Лапласа: определяется по таблице функции Лапласа: 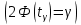
|
|
|
|
 Скачать 326.99 Kb.
Скачать 326.99 Kb.