Группировка стат таблиц. Группировка статистических данных.Статистические таблицы. Группировка статистических данных
 Скачать 223.75 Kb.
|
ГРУППИРОВКА СТАТИСТИЧЕСКИХ ДАННЫХГруппировка - это распределение единиц совокупности по группам в соответствии с группировочным признаком. Назначение группировки состоит в том, что этот метод обеспечивает обобщение данных, представление их в компактном, обозримом виде. На основе группировки рассчитываются сводные показатели по группам, появляется возможность их сравнения, изучения взаимосвязей между признаками. Виды группировок представлены на Схеме 2.1.  Схема 2.1 Виды группировок Сводка – это комплекс операций, включающих группировку единиц наблюдения, подсчет итогов по каждой группе и по всей совокупности в целом и представление результатов в виде статистических таблиц. Построение группировки начинается с определения группировочного признака. Признаком называется определенное свойство, которым обладает отдельная единица совокупности. По характеру их выражения признаки делятся на качественные и количественные. Качественные (атрибутивные) признаки – это такие значение, значение которых выражается текстом. Например, группировочный признак может иметь качественное выражение: группировка работников по полу, образованию; группировка розничного товарооборота по территориальному признаку, торговой сети по характеру товарного ассортимента и т.д. Количественные – это такие признаки, значение которых выражается числами. Они играют преобладающую роль в статистических исследованиях. примером группировок по количественным признакам может служить группировка работников по стажу работы, по возрасту, группировка торговых предприятий – по размеру площади торгового зала, численности торговых работников и т.п. По характеру вариации выделяют следующие виды признаков: альтернативные – принимают только два значения "да" или "нет"; дискретные – значение которых выражены целыми числами; непрерывные – значение которых выражены вещественными числами. При осуществлении любой группировки решается вопрос об определении числа выделяемых групп. При группировке по количественному признаку вопрос о числе групп решается на основе выделения однородных, близких по значению признака единиц совокупности. Необходимо, чтобы каждая группа характеризовала существенные типы явления. Число единиц в выделенных группах должно быть достаточным, чтобы характеристики, рассчитанные для отдельных групп были статистически устойчивыми. Количество выделяемых групп зависит от вариации признака, числа наблюдений, а также от количества отдельных возможных значений признака, т.е. от числа вариант признака. При небольшом числе вариант признака, положенного в основу группировки, каждая варианта представляет отдельную группу. Часто это альтернативный или дискретный признак. Если число вариант велико (непрерывный признак), то значения группировочного признака для отдельных групп указываются в интервалах "от - до". Для этого всю область изменения признака разбивают на несколько интервалов и считают сколько элементов попадает в отдельный интервал. Интервал - количественное значение, отделяющее одну единицу (группу) от другой, т.е. он очерчивает количественные границы группы. Как правило, величина интервала представляет собой разность между максимальным и минимальным значениями признака в каждой группе. Вопрос о количестве групп и величине интервала следует решать с учетом множества обстоятельств, прежде всего, исходя из целей исследования, значения изучаемого признака и т.д. Количество групп и величина интервала связаны между собой: чем больше образовано групп, тем меньше интервал, и наоборот. Количество групп зависит от числа единиц исследуемого объекта и степени колеблемости группировочного признака. При небольшом объеме совокупности нельзя образовывать большое число групп, так как группы будут малочисленными. При определении количества групп необходимо стремиться к тому, чтобы были учтены особенности изучаемого явления. Поэтому количество групп должно быть оптимальным, в каждую группу должно входить достаточно большое число единиц совокупности, что отвечает требованию закона больших чисел. Определить оптимальное количество групп с равными интервалами можно по формуле американского ученого Г.Стерджесса, предусматривающую выделение оптимального числа групп:  , гдеN– численность единиц совокупности. Формула Стерджесса используется при условии, что применяются равные интервалы в группах и при этом распределение единиц совокупности по данному признаку приближается к нормальному. Интервалы могут быть равными и неравными, открытыми и закрытыми. Группировку с неравными интервалами надо использовать если размах вариации признака в совокупности велик, неравные интервалы применяются как прогрессивно возрастающие или убывающие. В этом случае границы каждого интервала устанавливаются исследователем. Равные интервалы применяются в случаях, когда изменение признака внутри совокупности происходит равномерно. Расчет величины интервала при равных интервалах производится по формуле:  ,где - величина отдельного интервала, xmax - максимальное значение признака в исследуемой совокупности, xmin - минимальное значение признака в исследуемой совокупности. n - число групп, Группировки с равными интервалами целесообразны в тех случаях, когда вариация проявляется в сравнительно узких границах и распределение является практически равномерным (например, при группировке рабочих одной профессии по размеру заработной платы, посевов пшеницы - по урожайности). Пример 2.1. Требуется произвести группировку с равными интервалами по данным об уровне стипендии студентов в институте, которая в 2003 году колебалась в пределах от 850 до 1000 руб, и необходимо выделить 5 групп, то величина интервала, чел.: Если в результате деления получится дробное число и возникнет необходимость в округлении, то округлять нужно в большую сторону. Прибавляя к минимальному значению признака (в данном случае 850 руб.) найденное значение интервала, получаем верхнюю границу первой группы, руб.: 850 + 30 = 880. Прибавляя далее значение интервала к верхней границе первой группы, получаем верхнюю границу второй группы: 880 + 30 = 910 и т.д. В результате получим такие группы студентов по размеру выплачиваемой стипендии, руб: 850 – 880; 880 – 910; 910 – 940; 940 – 970; 970 – 1000. В этом распределении может иметь место неопределенность: какой группе, например, отнести студента со стипендией в 880 руб., к первой или ко второй? Здесь используют принцип единообразия – левое число в интервале включает в себя обозначенное значение, а правое – не включает. Значит, студент, получающий 880 руб. должен быть отнесен ко второй группе. Аналогично поступается в отношении всех остальных групп. При исследовании экономических явлений могут применяться неравные(прогрессивно возрастающие или прогрессивно убывающие) интервалы. Пример 2.2 По численности работающих промышленные предприятия могут быть разбиты на группы: до 200 человек, 200 - 300, 300 - 400, 400 - 600, 600 - 1000, 1000 и более человек. Это объясняется тем, что количественные изменения размера признака имеют неодинаковые значения в низших и высших по размеру признака группах: изменение количества работающих на 50-100 человек имеет существенное значение для мелких предприятий, а для крупных - не имеет. Закрытыми называют интервалы, у которых имеются верхняя и нижняя границы. Открытые – это те интервалы, у которых указана только одна граница: верхняя – у первого, нижняя – у последнего. Например, группы коммерческих банков по уровню дохода работающих в них сотрудников (тыс.руб.): до 10; 10 – 20;; 20 – 30; 30 – 40; 40 и более. Различия в целевом назначении группировки выражаются в существующей в нашей статистике классификации группировок: типологические, структурные, аналитические. Типологическая группировка – это разбиение разнородной совокупности на отдельные качественно однородные группы и выявление типов элементов явлений. Структурная группировка служит для исследования совокупности по одному признаку и предназначена для изучения состава однородной совокупности. После того, как в результате сводки статистические данные сгруппированы, они, как правило, представляются в виде таблицы. Макет таблицы для представления результатов структурной группировки может выглядеть следующим образом: Название таблицы
Здесь в первой графе указываются варианты (интервалы) значений признака для отдельных групп по возрастанию или убыванию. Аналитические группировки служат для выявления аналитической зависимости между группировочными признаками. При построении аналитических группировок важно правильно определить признак-результат и признак-фактор. Признак, влияние которого на другие признаки исследуется, называется признаком-фактором. Признак, испытывающий влияние факторного, называется признаком-результатом. Чтобы установить связь между признаками аналитическая группировка осуществляется по признаку-фактору. Затем по каждой группе отбираются соответствующие значения признака-результата и рассчитывается его среднее значение. Сопоставляя изменение средних значений признака-результата от группы к группе с изменениями признака-фактора можно сделать вывод о наличии или отсутствии взаимосвязи, а также о ее направлении. Различие групповых средних позволяет утверждать, что признаки взаимозависимы. Если изменение величины признака-фактора в определенном направлении вызывает изменение величины признака-результата в том же направлении, то связь прямая, в противном случае - связь обратная. Макет таблицы для представления результатов аналитической группировки может выглядеть следующим образом: Название таблицы
Здесь в первой графе указываются варианты (интервалы) значений признака-фактора для отдельных групп по возрастанию или убыванию. Группировка, выполненная по одному признаку называется простой. При анализе разнородных данных, например, при анализе материала, собранного в различные периоды времени, относящегося к различным отраслям промышленности, возникает необходимость применения вторичной группировки. Вторичнаягруппировка, или перегруппировка сгруппированных ранее данных применяется когда группировки построенные в разное время или для разных объектов могут оказаться несопоставимыми из-за различного числа выделенных групп или несовпадения границ интервалов. Применяют два способа образования новых групп. Первым, наиболее простым и распространенным способом является изменение (чаще укрупнение) первоначальных интервалов. Второй способ получил название долевой перегруппировки и состоит в образовании новых групп на основе закрепления за каждой группой определенной доли единиц совокупности. Проиллюстрируем методику вторичной группировки на (Примере 2.3). Пример 2.3. Распределение персонала строительной фирмы по уровню дохода (данные условные):
Произведем перегруппировку данных, образовав новые группы с интервалами до 5, 5 - 10, 10 - 20, 20 - 30, свыше 30 тыс. руб. В первую новую группу войдет полностью первая группа сотрудников и часть второй группы. Чтобы образовать группу до 5 тыс. руб., необходимо от интервала второй группы взять 1 тыс. руб. Величина интервала этой группы составляет 6 тыс. руб. Следовательно, необходимо взять от нее 1/6 (1:6) часть. Аналогичную же часть во вновь образуемую первую группу надо взять и от численности работающих, то есть 20х1/6=3 чел. Тогда в первой группе будет работающих: 16 + 3 = 19 чел. Вторую новую группу образуют работающие второй группы за вычетом отнесенных к первой, то есть 20 - 3 = 17 чел. Во вновь образованную третью группу войдут все сотрудники третьей группы и часть сотрудников четвертой. Для определения этой части от интервала 18 - 30 (ширина интервала равна 12) нужно добавить к предыдущему 2 (чтобы верхняя граница интервала была равна 20 тыс. руб.). Следовательно, необходимо взять часть интервала, равную [2:12 = 1:6]. В этой группе 74 человека, значит надо взять 74х(1:6)=12 чел. В новую третью группу войдут 44 +12 = 56 чел. Во вновь образованную четвертую группу войдут 74 - 12 = 62 чел., оставшихся от прежней четвертой группы. Пятую вновь образованную группу составят работающие пятой и шестой прежних групп: 37 +9 = 46 чел. В результате получим следующую новую группу:
Многомерная группировка производится по двум и более признакам. Частным случаем многомерной группировки является комбинационная группировка, базирующаяся на двух и более признаках, взятых во взаимосвязи, в комбинации. Как уже было отмечено, характеристика одной и той же качественной стороны изучаемого явления может быть дана с помощью набора признаков. Например, для характеристики технического уровня развития предприятий могут быть использованы следующие показатели: удельный вес активной части промышленно-производственных основных фондов, удельный вес автоматических машин и оборудования в составе рабочих машин и оборудования; электровооружснность труда, машиновооруженность рабочих; степень охвата механизированным трудом, коэффициент обновления машин и оборудования и т.д. Характеризуя, таким образом, каждую единицу совокупности набором признаков, можно рассматривать эту единицу как точку в n-мерном пространстве, а задача многомерной группировки будет состоять в выделении точек, составляющих однородные группы единиц. Иными словами, такая группировка осуществляется не последовательно по отдельным признакам, а одновременно по комплексу признаков. Комбинационной называется группировка, выполненная по двум и более признакам, взятым в сочетании (комбинации). Макет комбинационной таблицы выглядит следующим образом: Наименование таблицы
Здесь nij - частота совместного появления значения i признака-фактора (i = 1, 2,..,m) и значения j признака результата (j = 1,2,...,k). Результаты комбинационной группировки по большому количеству признаков даже при небольшом числе интервалов группировки становятся трудно обозримыми, и таблица теряет свое важнейшее преимущество - наглядность. Поэтому нецелесообразно составлять комбинационные таблицы по сочетанию более чем трех признаков и при количестве интервалов более четырех. Использование комбинационных таблиц и системы взаимосвязанных группировок позволяет провести глубокий и всесторонний анализ сложных общественных явлений. Мерой близости (сходства) между единицами могут служить различные критерии. В зависимости от выбранного критерия существуют различные методы многомерной группировки. Применение методов многомерной группировки связано с большой вычислительной работой и требует использования электронной вычислительной техники. С помощью специальных алгоритмов на ЭВМ осуществляется формирование групп, в которых единицы совокупности объединяются на основании близости по всему комплексу признаков. При осуществлении многомерных группировок могут быть использованы два основных подхода: Суть первого состоит в том, что каждая единица совокупности, характеризующаяся набором из nпризнаков, рассматривается как точка в n -мерном пространстве. Множество точек (единиц совокупности) разделяется на однородные группы. Мерой близости точек (сходства единиц совокупности) могут служить различные критерии. В кластерном анализе, например, в качестве критерия близости используют евклидово расстояние. Второй подход заключается в расчете обобщающего показателя по комплексу группировочных признаков и проведении простой группировки по этому обобщающему показателю. Разновидностью такого подхода является метод многомерных средних. После того, как в результате сводки статистические данные сгруппированы, они, как правило, представляются в виде таблицы. Это наиболее рациональная, наглядная и компактная форма представления статистического материала. Статические таблицы Статистическая таблица представляет собой систему строк и столбцов, в которых в определенной последовательности и связи излагается статистическая информация. По логическому содержанию таблица представляет собой "статистическое предложение", основными элементами которого являются подлежащее и сказуемое. Подлежащим таблицы называется объект, который характеризуется цифрами, обычно представляется в левой части таблицы, в наименовании строк. Сказуемое таблицы образует система показателей, которыми характеризуется объект изучения, то есть подлежащее таблицы. Сказуемое формирует верхние заголовки и представляет содержание граф с логическим, последовательным расположением показателей слева направо. Над таблицей помещается заголовок, отражающий в сжатой форме ее основное содержание, время и место, к которым относятся изложенные в таблице данные. Табличной называется такая форма расположения числовой информации, при которой число располагается на пересечении четко сформулированного заголовка по вертикальному столбцу, называемому графой, и названия по соответствующей горизонтальной полосе - строке. Данные статистических таблиц используются для целей оперативного руководства, научного анализа, позволяющего вскрыть взаимосвязи и имеющиеся резервы. Различие целей сказывается на характере подлежащего. В зависимости от характера подлежащего различают три вида таблиц: простые, групповые, комбинационные. Простыми таблицами называются статистические таблицы, в подлежащем которых нет группировок. Простые таблицы бывают: перечневые (подлежащее – перечень единиц, составляющих объект изучения); территориальные (дается перечень территорий, стран, областей, городов и пр.); хронологические (в подлежащем приводятся периоды времени или даты) Примером простой таблицы является таблица 2.1, в которой приведена структура макроэкономического показателя – использованного ВВП России. Таблица 2.1 Использованный ВВП РФ (в процентах к итогу в фактически действующих ценах)
Групповыминазываются таблицы, в подлежащем которых изучаемый объект разделен на группы по какому-либо признаку. Простейшим видом групповых таблиц являются ряды распределения. Групповая таблица может быть более сложной, если в сказуемом дополнительно приводятся ряд показателей, характеризующих группы подлежащего. Такие таблицы часто используются в целях сопоставления обобщающих показателей по группам. Таблица 2.2 Структура работников промышленной компании «Фатум»
Комбинационными – таблицы, где в подлежащем дана группировка единиц совокупности по двум и более признакам, взятым в комбинации: каждая из групп, построенная по одному признаку, разбивается в свою очередь, на подгруппы по какому-либо другому признаку и т.д. Таблица 2.3 Зависимость заработной платы водителей от квалификации и процента выполнения норм выработки
Комбинационные таблицы позволяют характеризовать типические группы, выделенные по нескольким признакам и связь между ними. Последовательность разбиения единиц совокупности на однородные группы по признакам определяется либо важностью одного из них в их комбинации, либо порядком их изучения. В отличие от простых групповые и комбинационные таблицы обладают важными аналитическими свойствами: они позволяют производить наглядные сравнения и вскрывать существенные связи и различия в развитии явлений. Идея комбинационной таблицы состоит в том, что каждую из групп в групповой таблице разбивают на подгруппы по какому-либо признаку; выделенные подгруппы могут дальше расчленяться по следующему признаку и т.д. Цифровой материал может быть представлен абсолютными (численность населения РФ), относительными (индексы цен на продовольственные товары) и средними (среднемесячный доход служащего коммерческого банка) величинами. Таблицы могут сопровождаться примечанием, используемым с целью пояснения, в случае необходимости, заголовков, методики расчета некоторых показателей, источников информации и так далее. Для избежания ошибок при построении и оформлении таблиц необходимо соблюдать следующие правила: таблица должна быть небольшой по размеру, тогда ее легче проанализировать; целесообразнее построить несколько небольших таблиц, чем одну большую; название таблицы должно быть четким и ясным; цифровую информацию обычно размещают от частного к общему, то есть сначала показывают слагаемые, а затем подводят итог; если приводятся не все данные, а выделяются наиболее значимые из них, то сначала показывают итог, а затем выделяют "в том числе"; если показатели таблицы имеют одинаковые единицы измерения, их можно указать в названии таблицы; если единицы измерения различны, их нужно указывать в названиях колонок или строк; при построении таблиц используются следующие условные обозначения: при отсутствии показателя ставится прочерк; если отсутствуют сведения, ставится многоточие. цифровые данные целесообразно округлять, причем округление чисел следует показывать в таблице с одинаковой степенью точности; таблица может сопровождаться примечаниями, в которых указывают источники данных, более подробное содержание статистических показателей и т.п. Важно не только грамотно построить таблицу, но и уметь правильно произвести анализ ее данных. При этом не следует пересказывать содержание таблицы, иначе теряется смысл ее построения. Анализ следует начинать с общих итогов, которые раскроют содержание таблицы, дальше анализируются частные итоги, если нужно, производятся дополнительные расчеты. Графическое изображение статистических данных Кроме табличного и текстового методов изложения статистического материала, наглядным изображением статистических данных является графический материал. Графические изображения статистических данных облегчают их обобщение и анализ. Графики применяются для характеристики развития явления во времени, в пространстве, отображения структуры явления и структурных сдвигов, прогнозов хозяйственной деятельности, при контроле за выполнением плана, изучении взаимосвязи между явлениями. По способу построения графики делятся на диаграммы, картограммы и картодиаграммы. Самым распространенным видом графиков являются диаграммы, которые делятся на линейные, столбиковые, структурные, фигурные, знаки Варзара и др. Диаграмма — наиболее распространенная форма графических изображений статистических данных при помощи геометрических фигур, линий, точек. Применяются для наглядного сопоставления в различных аспектах (пространственном, временном и др.) независимых друг от друга величин: территорий, населения и т.д. Диаграмма столбиковая изображает статистические величины в форме удлиненных прямоугольников (столбиков) одинаковыми по ширине (т.к. это диаграмма одномерного измерения и величина показателя характеризуется высотой столбика).    Рис. 2.1 Виды диаграмм по форме геометрического образа (линейные, плоскостные, объемные) Столбиковую диаграмму, отражающую динамику явлений, можно превратить в ленточную, или полосовую диаграмму. Для их построения также используется система прямоугольных координат. Основания столбиков одинакового размера, представляющие собой периоды времени (годы, месяцы, дни), размещаются на оси абсцисс, а вершины столбиков соответствуют величине изучаемого показателя. Столбиковые диаграммы называют ленточными, если столбики расположены горизонтально в виде лент.  Рис.2.2 Пример построения столбиковой (а) и полосовой (б) диаграммы (cравниваются значения групп А,В,С,D,E) Разновидностью полосовой диаграммы является скользящая диаграмма. В скользящей полосовой диаграмме направленность полос определяется не их нулевыми точками, а условными значениями, по которым полосы смещаются друг против друга вправо и влево. Этой диаграммой можно графически изображать данные демографической статистики о вероятной продолжительности жизни людей в зависимости от пола и возраста. Линейные диаграммы (статистические кривые) - наиболее простой способ наглядного изображения статистических данных, когда изучаемое явление представляется в виде отрезков ломаной линии, называемой статистической кривой. Они применяются для характеристики и сравнения развития различных явлений во времени, пространстве, а также для отображения взаимосвязи между явлениями. Для построения линейной диаграммы используется прямоугольная система координат. На оси абсцисс (по горизонтальной шкале) откладываются равные отрезки, представляющие собой периоды времени, на ось ординат наносят масштаб для отображения уровня явления. Соединение точек, построенных на координатной системе, дает ломаную линию, представляющую собой закономерность развития явления. Примеры линейных диаграмм изображены ниже.   Рис.2.3 Линейные диаграммы Рекомендуется строить координатную сетку с учетом соотношения масштабов по осям координат примерно 1:1,5 (правило «золотого сечения»), т. е. с учетом соотношения масштабов по сторонам занятого графиком пространства по вертикали и горизонтали. Преимуществом линейных графиков является то, что на одном графике имеется возможность отображения закономерности нескольких явлений. Разновидностью линейных диаграмм являются контрольно-плановые графики, обеспечивающие оперативный контроль за ходом выполнения задания как за отдельные промежутки (дни, пятидневки), так и нарастающим итогом с начала периода. С 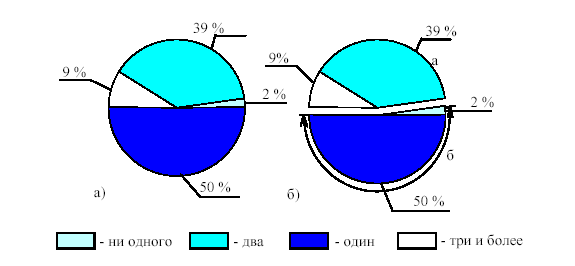 труктурные диаграммы применяются для изображения структуры явления и характеристики структурных сдвигов. При построении таких графиков состав совокупности выражается относительными величинами структуры, исчисленными в процентах. Они могут быть двух видов: столбиковые и круговые. Рис.2.4 Два вида структурной секторной диаграммы («Количество телевизоров в московской семье в 2000 г.») простая секторная диаграмма с группировкой долей Общая высота столбика и площадь круга отображают целое и принимаются соответственно за 100%. При построении круговой диаграммы необходимо проценты перевести в градусы, учитывая, что каждый процент равен 3,6° (360: 100). З  наки Варзара (по имени статистика В. Е. Варзара) являются разновидностью столбиковых диаграмм. Они позволяют отобразить на графике сложное явление, представляющее собой произведение двух показателей. «Знак Варзара» представляет собой прямоугольник, у которого один сомножитель принят за основание, другой за высоту, а вся площадь равна произведению. Рис.2.5. Данные о вкладах населения в Сбербанки региона в 1994 г. Оба показателя откладываются на шкалах (каждый на своей), третий (результат) изображается в виде прямоугольника в поле графика. На рисунке 2.5 средний размер вклада, умноженный на их число, дает общую сумму вкладов, что и отображается в виде площади (данные в центре прямоугольников, млрд. руб.) Статистические карты 
Рис. 2.6 География распределения районов по урожайности зерновых Применяется в тех случаях, когда возникает необходимость показать территориальное распределение какого-нибудь одного статистического признака между отдельными районами для выявления закономерностей этого распределения.   Картодиаграмма — это сочетание диаграммы с географической картой. В качестве изобразительных знаков в картограммах используются те или иные фигуры, которые размещаются на контуре географической карты. С помощью картодиаграммы можно выразить пространственную специфику в структурах изучаемых статистических совокупностей, особенности каждого района, как единого целого. Например, структурная или секторная картодиаграмма, характеризующая порайонные различия в структуре посевных площадей10 20 30 40 50 тыс. га Рис. 2.7.Площадь пахотных земель (по крупным землепользователям). (Цифры у диаграммы знаков указывают суммарную площадь пахотных земель в тыс. га) Кроме рассмотренных видов диаграмм в статистической практике встречаются и другие, более сложные, графические объекты статистических данных. Графический метод в статистике является продолжением и дополнением табличного метода. График позволяет сравнительно легко обнаружить на глаз ошибки расчетов, которые в табличной форме не были так заметны. Становится более выразительной сравнительная характеристика изучаемых показателей, тенденция развития изучаемого явления, лучше видны основные взаимосвязи. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||