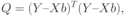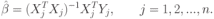ммфп. 1 Основные определения теории подобия и моделирования. Варианты постановки задач моделирования
 Скачать 493.39 Kb. Скачать 493.39 Kb.
|
|
1 Основные определения теории подобия и моделирования. Варианты постановки задач моделирования Моделирование – замещение одного объекта другим с целью получения информации о важнейших свойствах объекта оригинала с помощью объекта модели. Подобие – взаимно однозначное соответствие между 2 объектами при котором ф-ии перехода от параметров, характеризующих один из объектов, к параметрам др. объекта известны, а мат описание этих объектов могут быть преобразованы в тождественные. Модель – объект находящийся в отношении подобия к моделируемому объекту. Моделирование – исследование моделируемого объекта, базирующегося на его подобии модели и включающие построение, изучение модели и перенос полученных сведений на моделируемый объект. Задачи обучения: Применение моделирования для уяснения физических законов; Рассмотрение действия новых разработок и установок; Тренировки персонала действующих производственных объектов. Исследовательские задачи: Прямые задачи анализа – исследуемая сисма задается параметрами своих элов, параметрами исходного режима, структурой или уравнениями. Требуется определить реакцию сис-мы на действующие силы или сигнал. 2.Обратная задача анализа по известной реакции сис-мы требуется найти силы или сигналы, кот вызвали такую реакцию. 3.Задача синтеза-позволяет найти такие параметры системы при кот. процессы в системе будут носить желательный характер. 4.Индуктивные задачи. Проверка гипотез, уточнение ур-ний описывающих процессы в сис-ме, выяснения свойств элементов сис-мы. 2Классификация моделей:  А) Степень полноты модели: 1.Полное подобие – подобие протекании во времени и пространстве основных процессов, т.е. тех, которые для данной цели исследования, достаточно полно определяют явления. 2.Неполное подобие протекание всех основных процессов подобных только частично (или во времени, или в пространстве). 3.Приближенное подобие допускается нарушение взаимно однозначного соответствия м/у моделью и объектом, или такое искажение процессов модели которая в данной постановке задачи приемлемо и оценивается аналитически или экспериментально. Б) Модели м. б.: 1.детерминированными(без учета случайных возмущений параметра); 2.стохастическими. В) Модели: 1.динамические– описание поведения объекта во времени; 2.статическое-описание объекта в фиксированный момент времени. Г) Модели: 1.дискретные модели - параметры объектов могут принимать значение из фиксированного набора состояний; 2.непрерывные – параметры системы могут принимать любое значение из заданного диапазона; 3.дискретно – непрерывные. Д)Мысленное моделирование: — Наглядное: 1.)Гипотетическое (в основе лежит гипотеза, к ним прибегают когда недостаточно знаний); 2.)Аналоговое моделирование(применение аналогий различного уровня). 3.)Макетирование(в основе лежит аналогичность протекания процессов) — Символическое основанно на использовании искусственных логических объектов, кот. замещают реальный объект и выражают его свойства системой знаков: 1.)Знаковое моделирование(основывается на использование условных обозначений для отдельных понятий и операций между ними);2.)Языковое моделирование(в основе лежит тезаурус – словарь освобожденный от всех неоднозначностей) − Математическое – процесс установления соответствующих заданному реальному объекту математического объекта и исследования данной модели. Классификация математического моделирования: а) Аналитическое моделирование– процесс функционирования системы описывается в виде функций, соотношений или логических условий. Аналитические модели могут быть исследованы следующими способами: 1) Аналитический способ, т.е. получение в общем виде явной зависимости для искомых параметров. 2) Численный способ (дают численный результат для конкретных начальных условий ) 3)Качественный способ (получение свойств решения, наличие разрывов функции, дифференцируемость и т.д. ) б) Имитационное моделирование, при построении модели имитирующие элементарные явления, при сохранении их логической структуры и последовательности протекания во времени. в) Комбинированное моделирование(имитац-е и аналитического) Е)Реальное моделирование заключается в исследовании характеристик на реальном объекте. 1)Натуральное моделирование: - производственный эксперимент (реально работающие устройства); - комплексные сочетания (моделируются специальные условия функционирования) - научный эксперимент 2) Физическое моделирование, исследования проводят на установках, которые сохраняют природу физических явлений. -моделирование в реальном времени; -моделирование в нереальном масштабе времени; -замороженное моделирование 3. Этапы моделирования.Уровни мод-я.Требования к моделям Этап 1.Уяснение и постановка задачи на физич.уровне, процесс схематизации явления и выделение его существенных особенностей. Этап2.После выделения сущест венных факторов происходит перевод данных на язык мат-х понятий.Часто опираются на физич. з-ны принципы ТВ,… Этап3. После построения модели следует проводить проверку логической непроворечивости и её адекватности явлению Этап4.Все существенные данные из перечня параметров должны входить в матем-ю формулировку задачи.Справедливость модели проверяется по результатам решения теоретической задачи и сопоставления полученного результата с реальной ситуацией. Уровни моделирования 1.Микроуровень (использует мат модели описывающие физическое состояние и процессы на сплошных средах). К типичным исследованием по параметрам относятся эл. потенциаллы, давление, плотность. 2.Макроуровень (в качестве объектов моделирования выделяют – отдельные функионально законченные элементы). 3.Метауровень (на этом уровне, путем дальнейшего абстрагирования физических процессов, полученные модели описывающие информационные процессы). Требования к математическим моделям 1.Адекватность модели, т.е. отражаются заданные св-ва с заданной точностью. 2.Точность модели, определяется как степень совпадения значений выходных параметров модели и объекта. Чаще всего точность выражается погрешностью. 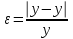 ; y-измеренное значение вых.параметра; ; y-измеренное значение вых.параметра;  -знач-е вых.параметра,рассчит. по модели -знач-е вых.параметра,рассчит. по модели3.Универсальность определяется числом и составом учитываемых в моделях внешних и выходных параметров. 4.Экономичность, характеризуется затратами вычислительных ресурсов для реализации модели 4Два подхода к моделированию 1) Классический: рассматривает объект моделирования путем перехода от частного к общему и синтезирует модель путем слияния ее компонентов разрабатываемыми отдельно. взаимосвязано м/у отдельными частями модели рассматриваются как отражения связи м/у подсистемами объекта . Реальный объект разрабатывается на отдельные подсистемы, т.е. выбираются исходные данные Д и ставятся цели Ц для нахождения этих подсистем. По отдельной совокупности исходных Д с учетом цели Ц, формируется компонент к будущей модели. Совокупность объединяется в модель(от частного к общему)  2) Системный: Предлагает последовательный переход от общего к частному. В основе моделирования лежит общая цель. На основе исходных данных и цели Ц формулируются требования Т к модели. На базе требований формируется подсистемы П и элементы Э будущей модели, кот на основе критерия выбора формируют состав модели М.  5Математические схемы описания моделирования. Обьект моделирования описывается след. переменными: -Входные воздействия на систему 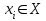 -Воздействия внешней среды  -Внутренние параметры системы  -Выходные характеристики   Процесс функционирования объекта описывается оператором  Совокупность зависимостей вых. характеристик объекта Совокупность зависимостей вых. характеристик объекта  называется выходной траекторией. называется выходной траекторией.Схемы описания модели: 1.непрерывно-детерминированная схема – D – схемы, используется для описания модели систем функционирования непрерывно во времени, параметры кот м. принимать любое значение без учёта случ.возмущений этих параметров(диф.ур-я,сис-мы диф.ур-й ). 2.Дискретно-детерминированная схема - F-схемы, объект представляется в виде автомата(цифровой схемы),перерабатывающего дискретную информацию и изменяющего своё внутр.состояние в заданный момент времени. 3.Дискретно-стахастические схемы -P – схемы, объекты представляются дискретными преобразователями информации с памятью,функционирование кот определяется состоянием этой памяти и м.б. описана статистически 4.Непрерывно стохастические схемы Q - схемы, их объект мод-я представляется как сис-ма,исполняющая заявки на обслуживание. 6 Статистический м-д исследования модели М-д статических испытаний (Монте-Карло) представляет собой м-д получения с помощью ЭВМ статистических данных о процессах происходящих в моделируемой сис-ме. Сущность м-да в построении моделируемого алгоритма для процессов функционирования исследуемой сис-мы, имитирующем поведение и взаимод-я элементов сис-мы с учетом случайных взаимодействий. Выделяют 2 области применения м-да Монте-Карло: 1) Для моделирования объектов 2) численный м-од решения детерминированных задач. Алгоритм применения м-да М.-К. для модел-я: 1.разработка детерминированной модели,описывающей функционирование объекта 2.Получение случайных чисел,соответствующих законам распределения стахостич. параметров объекта, влияние кот необходимо исследовать 3.расчёт значений вых параметров модели во всём диапазоне изменений детерминированныхпараметров для всех получившихся случ параметров 4.полученный набор значений рассматривается как реализация случайного процесса,т.е. знач-е вых параметров в кажд точке изменения детерминированных пар-ов рассматриваетси как выборка случайной величины и обрабатывается статистически(мат.ожидание,дисперсия,…) 7Способы получения случайных чисел. 1.аппаратный, случайное число вырабатываются с помощью случ.датчика.  Достоинства: 1) Запас чисел неограничен: 2) не использ. ресурсы ЭВМ Недостатки: 1) требуется периодическая проверка качества последовательности случайных чисел; 2) нельзя воспроизвести одинаковые последовательности; 3) необходимо специальное устройство. 2.табличный реализуется путем заполнения памяти ЭВМ некоторой проверенной последовательностью с.ч. Д:1) не требуется проверка качества последовательности 2)м. воспроизводить одинак. последовательности. Н:1) Запас чисел ограничен 2) нерациональное использовпание ресурсов ЭВМ 3.алгоритмический основан на формировании с.ч. в ЭВМ по некоторому алгоритму. Д:1)Возможность воспроизведения одинак. последовательностей; 2)Однократная проверка кач-ва последовательности 3) малые затраты ресурсов ЭВМ Н:1) Запас чисел ограничен 8 Получение последовательностей с.ч. с заданным з-ом распределения плотности вер-ти 1.Масштабирование Если необходимо получить последовательность с.ч. с равномерным з-ком распределения в диапазоне [a;b], то  , где , где  - с.ч. из последовательности с равномерным з-ком распределения [0;1]. Если нужно получить с.ч. с нормальным з-ом распределения с заданными my, - с.ч. из последовательности с равномерным з-ком распределения [0;1]. Если нужно получить с.ч. с нормальным з-ом распределения с заданными my,  , то , то  , где x-с.ч. с норм з-м распределения .ч. анными еления.ч. с нормальнымности вер-титерминированных пар-ов рассматриваетси как выборка случайной величины и обрабатыв , где x-с.ч. с норм з-м распределения .ч. анными еления.ч. с нормальнымности вер-титерминированных пар-ов рассматриваетси как выборка случайной величины и обрабатыв2.Преобразование закона распределения Если с.в. имеет плотность распределения  , то распределение с.в. , то распределение с.в.  ,где ,где  Чтобы получить  принадлежащее последовательности с распределением принадлежащее последовательности с распределением  , необходимо решить интегральное уравнение: , необходимо решить интегральное уравнение: , где , где  - случайная величина с распределением [0;1] - случайная величина с распределением [0;1]Для пересчета в нормальный з-н распределения с параметрами , используется след-е ф-лы:   3.Приближенный универсальный способ получения с.ч. на основе кусочной аппроксимации ф-ии плотности В. Алгоритм получения с.ч: 1) генерируется с.ч. равномерно распределенное в интервале [0;1] 2) по этому с.ч. выбирается номер интервала 3) генерируется с.ч.  равномерно распределенное в интервале [0;1] равномерно распределенное в интервале [0;1]4) рассчитывается  , где , где  - с.ч. приближенно распределенное по требуемому з-ну. - с.ч. приближенно распределенное по требуемому з-ну.9Составление модели экспериментальным статическим путем. Постановка задачи планирования эксперимента. Пассивный и активный эксперимент.Принципы планирования Эксперимент - целенаправленно организованный опыт, содержащий наблюдение исследуемого явления в специально заданных условиях. Входн параметры x наз факторами, вых параметры наз откликом. Изучение ф-ния объекта основывается на анализе внешних воздействий X и соотв. им реакции системы Y. Связь м/у X и Y представляют в виде уравнений. Различают: 1.В пассивном эксперименте значениями факторов управлять нельзя. Уровни факторов принимают случ.значения. 2.Активный эксперимен-значения факторов задаются и поддерживаются неизменными на опред уровне. Цель планирования эксперимента-пролучение max информации об исследуемом объекте при min кол-ве опытов Используются след. принципы: 1.Отказ от полного перебора всех возможных состояний объекта 2.Постепенное усложнение структуры модели 3.Сопоставление рез-ов экс-та с величиной случ.помех 4.Принцип рандомизации опыта. Опыты проводятся таким образом,чтобы все переменные носили случ хар-р 5.Оптимальное планирование экс-та 10Корреляционный анализ По результатам проведения экс-та проводят корреляц.анализ, рассчит-ся коэф-т корреляции для каждой пары факторов и для факторов и ф-ии отклика  где XiXj-этоi ,j факторы или I -фактор иj-ф-я отклика SiSj-среднеквадратич отклонения Xi-значение i-го фактора N-кол=во опытов в экспероименте 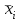 -средн.значение фактора -средн.значение фактораЕсли коэф. =1 или -1, то это значит что м/у параметрами сущ.тесная связь. Если =0, то связь отсутствует. Если”0”,то фактор исключается из модели;если1,-1 исключают фактор менее связанный с входн параметрами 11Регрессионный анализ Задача анализа-определение параметров экспериментальных факторных моделей 3 этапа: 1.статистич анализ рез-ов экс-та 2.получение коэф-ов регрессионной модели 3.оценка адекватности и работоспособности получ модели Факторную модель м. представить в след виде:  ,φ-ур-е регрессии,x-факторы,b-коэф-ты ур-я регрессии ,φ-ур-е регрессии,x-факторы,b-коэф-ты ур-я регрессииРезультаты экс-та представлены в виде  ,ε-аддитивная помеха с норм. з-ом распред-я ,ε-аддитивная помеха с норм. з-ом распред-яТ.к.в рез-те проведения экс-та всегда получаются случ.значения ф-ии отклика,то и рассчитанные знач-я коэф-ов модели b явл-ся оценками истинных значений коэф-ов модели β. Ф-ю φ(x)м. представить:  , βj-коэф ур-я регрессии,f()-j базисная ф-я , βj-коэф ур-я регрессии,f()-j базисная ф-яПредпосылки: 1.аддитивн помеха ε- случайная нормально распред вел-на с нулевым мат ожиданием и пост дисперсией 2.знач-е факторов в активном экс-те-это не случайн6ые величины 3.знач-е факторов в пассивном экс-те-случайные нормально распред-е велшичины 4.помехи в различных точках опыта не коррелированны 5.вектор-столбы базисных ф-ий, образованных значениями базисных ф-ий в кажд опыте должны быть линейно независимыми 12 Оценка параметров регрессионной модели Исходными данными для оценки параметров регресс модели явл-я данные о значениях факторов x и ф-ии отклика Y. Это информация представлена в виде:  n-кол-во факторов,N-кол-во опытов,Xij-знач-е j фактора в I опыте n-кол-во факторов,N-кол-во опытов,Xij-знач-е j фактора в I опыте . Значения базисных ф-ий в кажд опыте образуют матрицу базисных ф-ий: . Значения базисных ф-ий в кажд опыте образуют матрицу базисных ф-ий: fik-знач-е коэф-в в i опыте fik-знач-е коэф-в в i опытеНеобходимо определить значение вектора  . В кажд опыте знач-е ф-ии отклика можно представить в виде . В кажд опыте знач-е ф-ии отклика можно представить в виде  (ε-невязка).Для определения параметров модели невязку необход минимизировать для чего используется м-д наименьших квадратов. Составляется ф-я, представ собой сумму квадратов невязок: (ε-невязка).Для определения параметров модели невязку необход минимизировать для чего используется м-д наименьших квадратов. Составляется ф-я, представ собой сумму квадратов невязок: 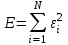 . Значение коэф-ов b находится таким образом,чтобы эта ф-я приняла min знач-е . Значение коэф-ов b находится таким образом,чтобы эта ф-я приняла min знач-еКоэф-ты при неизвестных переменных b образуют матрицу Ф: Ф=  ( ( -матрица базисных ф-ий) -матрица базисных ф-ий) Ф  Вектор-столбец:  Систему ур-ий для нахождения коэф-ов b принимает вид: Систему ур-ий для нахождения коэф-ов b принимает вид:Ф  Теоретическая частьОсновная задача пассивного эксперимента — по результатам наблюдений сделать некоторые выводы о параметрах математической модели эксперимента [1]. При этом вид ее предполагается известным, а параметры — неизвестными. Далее будет рассматриваться класс линейных регрессионных моделей эксперимента. В общем случае объект исследования представляется в виде схемы, представленной на рис. 9.1, где  — входные величины или факторы; — входные величины или факторы;  — —  -я выходная величина ( -я выходная величина (  ); );  — случайные неконтролируемые возмущения [12]. — случайные неконтролируемые возмущения [12].Под моделью объекта по  -му каналу понимают функцию -му каналу понимают функцию
Так как имеются случайные неконтролируемые возмущения, изменение функции (9.1) носит случайный характер, а потому для получения математического описания (9.1) применяются методы регрессионного анализа на основе статистических данных, накопленных в результате проведения эксперимента.  Рис. 9.1. Схема объекта исследования Применение метода пассивного эксперимента может быть успешным, если при его проведении соблюдаются необходимые условия, к которым относятся такие, как правильное определение времени регистрации данных, обеспечение независимости соседних измерений и входных переменных друг от друга, достаточный с точки зрения математической статистики объем экспериментальных данных [12]. Если функция не имеет бесконечных разрывов, то ее можно разложить в степенной ряд Тейлора:
где  , ,  , ,  , ,  — постоянные коэффициенты уравнения, оценки которых необходимо определить в результате постановки и проведения пассивного эксперимента; — постоянные коэффициенты уравнения, оценки которых необходимо определить в результате постановки и проведения пассивного эксперимента;  — число наиболее существенных входных величин, полученных в результате отсеивающего эксперимента. — число наиболее существенных входных величин, полученных в результате отсеивающего эксперимента.Пространство, в котором строится поверхность отклика – реакция выходной величины, называется факторным пространством . Для применения методов регрессионного анализа требуется выполнение ряда предпосылок [12], а именно: результаты наблюдений  выходной величины в точках факторного пространства представляют собой независимые случайные величины, распределенные по нормальному закону, а процесс изменения выходной величины должен быть стационарным во времени; выходной величины в точках факторного пространства представляют собой независимые случайные величины, распределенные по нормальному закону, а процесс изменения выходной величины должен быть стационарным во времени;дисперсии 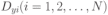 этих случайных величин должны быть равны друг другу (выборочные оценки дисперсий однородны); этих случайных величин должны быть равны друг другу (выборочные оценки дисперсий однородны);все значения входных величин должны измеряться с пренебрежимо малой ошибкой по сравнению с ошибкой измерения выходной величины; входные величины не должны коррелировать между собой; все соседние измерения по каждой  -й входной величине должны быть независимы. -й входной величине должны быть независимы.Число коэффициентов уравнения (9.2) определяет объем эксперимента. Поэтому выбирают такой полином, который содержит как можно меньше коэффициентов, но удовлетворяет требованию простоты и адекватности, под которой понимается способность модели предсказывать результаты эксперимента в некоторой области с требуемой точностью. Часто на предварительной стадии исследования объекта выбирают полином первой степени (включая первую сумму в уравнении (9.2), т. е. в разложении Тейлора), предполагая, что параметры объекта лежат в области, в которой расположен экстремум исследуемой функции (выходная величина системы – отклик), и поэтому объект описывается линейной моделью. Если же эта линейная модель оказывается неадекватной, то в нее включают члены парного взаимодействия 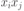 (включая вторую сумму в уравнении (9.2), т. е. в разложении Тейлора), а при необходимости увеличивают степень полинома до тех пор, пока модель не окажется адекватной [12]. (включая вторую сумму в уравнении (9.2), т. е. в разложении Тейлора), а при необходимости увеличивают степень полинома до тех пор, пока модель не окажется адекватной [12].В результате регрессионного анализа результатов пассивного эксперимента находят оценки коэффициентов уравнения регрессии 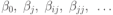 . .1. План экспериментаРассмотрим эксперимент, в котором проводится  измерений зависимой переменной измерений зависимой переменной  в некоторых точках факторного пространства [1]. Обозначим через в некоторых точках факторного пространства [1]. Обозначим через  наблюдаемое значение зависимой переменной наблюдаемое значение зависимой переменной  в в  -м опыте в точке -м опыте в точке . .Здесь  — значение переменной — значение переменной  в в  -м опыте. -м опыте.Определение 1. Набор точек  называется планом эксперимента. Точки при этом не обязательно должны быть различными. Матрица вида называется планом эксперимента. Точки при этом не обязательно должны быть различными. Матрица вида
называется матрицей плана эксперимента. Если обозначить различные точки плана через  , то совокупность таких точек называется спектром плана. , то совокупность таких точек называется спектром плана.Определение 2. Нормированным планом  называют совокупность величин называют совокупность величин  ; ;  , где , где 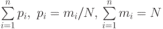 . .В пассивном эксперименте задача построения плана не рассматривается. Матрица плана (9.3) предполагается известной (заданной) или является предопределенной условиями проведения эксперимента [1]. Задача исследователя в пассивном эксперименте состоит в выполнении наблюдений над выходной (зависимой) переменной в точках, определяемых матрицей плана, и последующем анализе их результатов. Примечание. В случае, когда регрессионная модель строится непосредственно по измерениям без предварительного усреднения, для того чтобы произвести оценку свободного члена, в модели необходимо представить матрицу плана в виде
2. Одномерная регрессионная модель экспериментаВ общем случае вид функции отклика неизвестен. Будем предполагать, что функция отклика является одномерной и представима в виде
где: 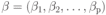 есть есть 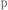 -мерный вектор неизвестных параметров; -мерный вектор неизвестных параметров; — известные функции, которые называются еще базисными функциями. — известные функции, которые называются еще базисными функциями.Под регрессионной моделью эксперимента будем понимать линейную по параметрам  функцию отклика (9.5). функцию отклика (9.5).В качестве примера рассмотрим функцию отклика  Построим матрицу планирования по заданным измерениям входной переменной 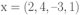 . В соответствии с (9.4) будем иметь . В соответствии с (9.4) будем иметь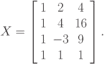 Еще один пример. Пусть функция отклика имеет вид 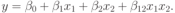 Значения независимых переменных равны следующим значениям:  . .Тогда матрица планирования будет иметь такой вид, что в верхней строчке ее будут указаны аргументы функции отклика  где  — фиктивная переменная. — фиктивная переменная.3. Оценивание параметров одномерной функции откликаВ случае, когда одномерная функция отклика является линейной относительно неизвестных параметров, т. е.  в произвольной точке  по результатам наблюдений (измерений) в точках по результатам наблюдений (измерений) в точках  , где , где 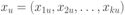 , задаваемых матрицей плана (планирования) , задаваемых матрицей плана (планирования) 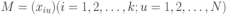 , наилучшая оценка в смысле метода наименьших квадратов равна , наилучшая оценка в смысле метода наименьших квадратов равна
если ранг матрицы планирования равен числу неизвестных параметров, т. е.  , где , где 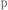 — число неизвестных параметров [1]. — число неизвестных параметров [1].Оценка параметров по формуле (9.6) называется оценкой по наблюдениям полного ранга, т. е. когда  . В этом случае формула (9.6) вытекает из так называемого нормального уравнения . В этом случае формула (9.6) вытекает из так называемого нормального уравнения
где 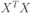 — информационная матрица. — информационная матрица.В методе наименьших квадратов минимизируется функционал (скалярная величина)
где  — вектор неизвестных параметров, подлежащих оценке. — вектор неизвестных параметров, подлежащих оценке.Оценка параметров по формуле (9.6) доставляет минимум функционалу (9.8). При подстановке (9.6) в (9.8) получающаяся величина называется остаточной суммой квадратов — RSS (Residual Sum of Squares). 4. Оценивание параметров многомерной функции откликаВ случае, когда имеются несколько выходных переменных — функций отклика, для каждой функции отклика можно произвести оценку параметров уравнения регрессии по формуле (9.6) с указанием нижнего индекса, относящегося к данной функции. Например, если имеется  функций отклика, то оценка вектора параметров по методу наименьших квадратов может быть найдена как функций отклика, то оценка вектора параметров по методу наименьших квадратов может быть найдена как
Общая оценка вектора параметров многомерной функции отклика будет определяться в виде
где  — символ транспонирования. — символ транспонирования.13Построение модели на основе пассивного эксперимента. Расчёт доверительных интервалов для коэф-ов ур-я регрессии.Проверка адекватности регрессионной модели После построения мат модели в виде ур-я регрессии выясняется значимость коэф-ов ур-й и адекватность полученной модели.Для модели рассчит.остаточная дисперсия:  ,где Nв-кол-во коэф-ов в регрессии,yi-знач ф-ии отклика по рез-ам эксперимента, ,где Nв-кол-во коэф-ов в регрессии,yi-знач ф-ии отклика по рез-ам эксперимента,  -знач ф-ии отклика по расчётам модели. -знач ф-ии отклика по расчётам модели.Остаточная дисперсия м.б. использована как оценка дисперсии ошибки эксперимента: 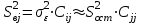 По критерию Стьюдента определяем значимость коэф:  Далее находиться табличное значение коэфф. Стьюдента:  Если рассчитанное значение больше табличного, то считается что коэффициент значимый. Если рассчитанное значение больше табличного, то считается что коэффициент значимый.Для значимых коэфф. можно рассчитать доверительный интервал:  Проверка адекватности модели проводиться по критерию Фишера.Опред средн дисперсией:  , ,  -средн знач-е отклика по результатам -средн знач-е отклика по результатамНаходим наблюдаемое знач-е критерия Фишера: 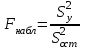 . Расчетное значение критерия Фишера сравнивается с табличным. Если расчетное больше табличного, модель считается адекватной. . Расчетное значение критерия Фишера сравнивается с табличным. Если расчетное больше табличного, модель считается адекватной.17Сущность оптимизации.Параметры оптимизации.Критерий оптимиз-и.Целевая ф-я. Оптимизация заключается в нахождении оптимальных условий проведения данного процесса. Для оценки достижения оптимума, прежде всего, выбираются критерии оптимизации. Это некоторая численная характеристика исследуемого объекта. На основании этого критерия строится целевая функция (функция качества). Задача оптимизации заключается в поиске параметров, при которых целевая функция достигает экстремальных значений - оптимальный параметр. Целевая функция может содержать множество параметров , часть из которых являются управляемыми. Этими параметрами можно варьировать для поиска их оптимального значения. Остальные параметры не подлежат оптимизации. Управляющие параметры м.б. как непрерывные так и дискретные. Если экстремум целевой функции отыскивается в неограниченной области, его наз. безусловным экстремумом, а методы его поиска - безусловной оптимизацией. Целевая ф-я-представляет собой зависимость критерия оптимизации от параметров, влияющих на его значение. 19М-ды оптимизации. Аналитический м-д поиска экстремума Классификация методов оптимизации: 1)Аналитические методы (аналитический поиск экстремума, метод множителей Лагранжа, вариационные методы) 2) Методы мат. программирования: а) Геометрическое - используется при оптимизации ЦФ в виде полиномов. б) Линейное - оптимизация моделей с ЦФ и ограничениями в виде линейной функции. 3)М-ды поисковой оптимизации(м-д градиента, м-д наискорейшего спуска) Аналитические методы: В классическом подходе необходимыми условиями локального экстремума явл.  20Метод множителей ЛАГРАНЖА Метод множителей ЛАГРАНЖА применяется для нахождения оптимальных значений параметра , если на модель наложено ограничение в виде равенств. В этом случае задача оптимизации ставится так: необходимо найти оптимальные параметры модели если ЦФ задана в виде  и заданы ограничения в вида  . .Для решения этой задачи составляется ф-я Лагранжа:  , ,В этом случае экстремальные точки ф-ии  определяются реш-ем сис-мы ур-й,получаемой приравниванием нулю производных от ф-ии определяются реш-ем сис-мы ур-й,получаемой приравниванием нулю производных от ф-ии  по всем независимым переменным xk(k=1,…n) и по всем множителям Лагранжа по всем независимым переменным xk(k=1,…n) и по всем множителям Лагранжа  .Получаемая сис-ма ур-й: .Получаемая сис-ма ур-й: содержит  уравнений,из кот можно исключить m неопределённых множителей Лагранжа и найти координаты экстремальных точек xk(k=1,2…n) уравнений,из кот можно исключить m неопределённых множителей Лагранжа и найти координаты экстремальных точек xk(k=1,2…n)21Поисковая оптимизация Большинство методов предназначено для поиска локальных экстремумов без учета ограничений. Поэтому важное значение приобретает выбор начальной точки поиска  Локальные методы безусловной оптимизации делятся на: 1) Методы нулевого порядка, в них не используется информация ЦФ. (Методы одномерного поиска: деления отрезка пополам; Методы многомерного поиска- покоординатного спуска; случайного поиска) 2) Методы первого порядка (Градиентный), используется значение ЦФ и первых частных производных по параметрам ( методы градиента; наискорейшего спуска и т.д.) 3) Методы второго порядка, используют значение ЦФ и первых и вторых частных производных (Метод Ньютона) 22Метод покоординатного спуска. Алгоритм: 1) из текущей точки поиска выполняется пробный шаг в положит направлении одной из координатной осей  , k-номер шага поиска. Оценивается улучшение целевой ф-ии , k-номер шага поиска. Оценивается улучшение целевой ф-ии  . Если это условие выполняется,то это направление выбирается для дальнейшего поиска экстремума.В противн.случае исследуется отрицат направление вдоль оси,т.е.выполняется пробный шаг . Если это условие выполняется,то это направление выбирается для дальнейшего поиска экстремума.В противн.случае исследуется отрицат направление вдоль оси,т.е.выполняется пробный шаг , , 2) выполняется движение вдоль выбранного направления  до тех пор, пока выполняется условие до тех пор, пока выполняется условие  3)те же действия выполняются для всех остальных параметров оптимиз-и 4)если из полученной точки нельзя улучшить целевую ф-ию ни покакому парам-ру,тоуменьшают шаг оптимизации:  2) операции 2-4 повторяют до тех пор пока  23Метод градиента. 1)-в текущей точке поиска находится градиент целевой ф-ии:  .Рассчитывается единичный вектор направления:  2)-выполняется шаг поиска  Оценивается успешность поиска.Если Оценивается успешность поиска.Если  ,то в полученной точке определ-я нов направление и алгоритм повторяется.В противном случае уменьшается шаг: ,то в полученной точке определ-я нов направление и алгоритм повторяется.В противном случае уменьшается шаг:  3)-условие окончания поиска   Метод наискорейшего спуска Основным недостатком градиентного метода является необходимость частого вычисления производных от функции F(х). Этого недостатка лишен метод наискорейшего спуска, который заключается в следующем. В текущей точке вычисляется Grad F(X), и затем в направлении градиента ищется Min F(X). Практически это может быть осуществлено любым методом одномерной оптимизации (поиск по одному направлению – направление градиента), наиболее часто используется сканирование до первого локального минимума по направлению Grad F(X). В результате вдали от оптимума эффективность метода повышается, мы быстрее попадем в район оптимума, в окрестности которого эффективность метода снижается из-за частой смены направления поиска и приближается к эффективности метода градиента. В ряде случаев можно повысить скорость выхода в район оптимума предъявлением невысоких требований к точности поиска Min по направлению (задается величиной H – шагом поиска по направлению). Условием окончания может являться малость модуля градиента функции F(X): |Grad F(X)| < . Можно также использовать и малость приращений по переменным в результате шага, но только в том случае, если на данном шаге мы «проскочили» оптимум, иначе может оказаться, что малость шага обусловлена не близостью к оптимуму, а малостью коэффициента пропорциональности шага H. В ряде случаев используют уменьшение шага поиска оптимума по направлению после каждой смены направления. Условием окончания поиска в этом случае является достижение заданной малой величины шага. Метод наискорейшего спуска отличается от градиентного спуска способом определения величины Hk, которая находится из условия:  (*) (*)Такой выбор Hk Обеспечивает максимально возможное уменьшение функции F(X) вдоль направления ее антиградиента  В точке Х(K). В точке Х(K).Таким образом, для определения Hk на каждом шаге метода наискорейшего спуска решается одномерная задача минимизации функции ФK(H), для чего можно использовать рассмотренные выше методы одномерной оптимизации. 24М-ды мат программирования.Задача линейного программирования Линейное программ-е связано с исследованием и решением задач:дана сис-ма m линейно независ. ур-й с n неизвестными,наз-я сис-ой ограничений.  Требуется найти неотрицат знач-е переменных,обращающее в min целевую ф-ию(xi>=0):  (1) наз линейной формулой и удовлетвор ограничению(1) (1) наз линейной формулой и удовлетвор ограничению(1)Базисом наз любой набор из m переменных таких,что определитель составленный из коэф-ов при этих переменных не равен нулю.Остальные (n-m)переменных наз свободными.Решение сис-мы ограничений путём приравнивания к нулю свободных переменных наз базисным.Базисное решение,кот удовлетворяет неравенству xi>0,наз допустимым.Решение задачи оптимизации лежит среди допустимых базисных решенй. |