Расчёт параметров и характеристик идеального (резкого) pnперехода
 Скачать 1.15 Mb. Скачать 1.15 Mb.
|
                                      Лабораторная работа № 2 Тема: Расчёт параметров и характеристик идеального (резкого) p-n-перехода Цель работы: освоить методику расчёта важнейших параметров и характеристик идеального p-n-перехода и усвоить их взаимосвязь 1 Краткие теоретические сведения о параметрах контактов металл-полупроводник и р-n-перехода. Основные расчетные соотношения Контактная разность потенциалов контакта металл – полупроводник: 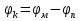 , (2.1) , (2.1)где 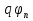 – термодинамическая работа выхода электронов из полупроводника, – термодинамическая работа выхода электронов из полупроводника,  – термодинамическая работа выхода электронов из металла (рисунок 2.1). – термодинамическая работа выхода электронов из металла (рисунок 2.1).Потенциал (высота) барьера Шоттки: 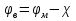 , (2.2) , (2.2)где  – сродство к электрону, эВ. – сродство к электрону, эВ.Ширина области пространственного заряда (ОПЗ) в полупроводнике (рисунок 2.1, б):  (2.3) (2.3)где 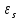 – диэлектрическая проницаемость полупроводника; еь электрическая постоянная; V – величина приложенного к контакту напряжения смещения; N – концентрация примеси в полупроводнике. – диэлектрическая проницаемость полупроводника; еь электрическая постоянная; V – величина приложенного к контакту напряжения смещения; N – концентрация примеси в полупроводнике.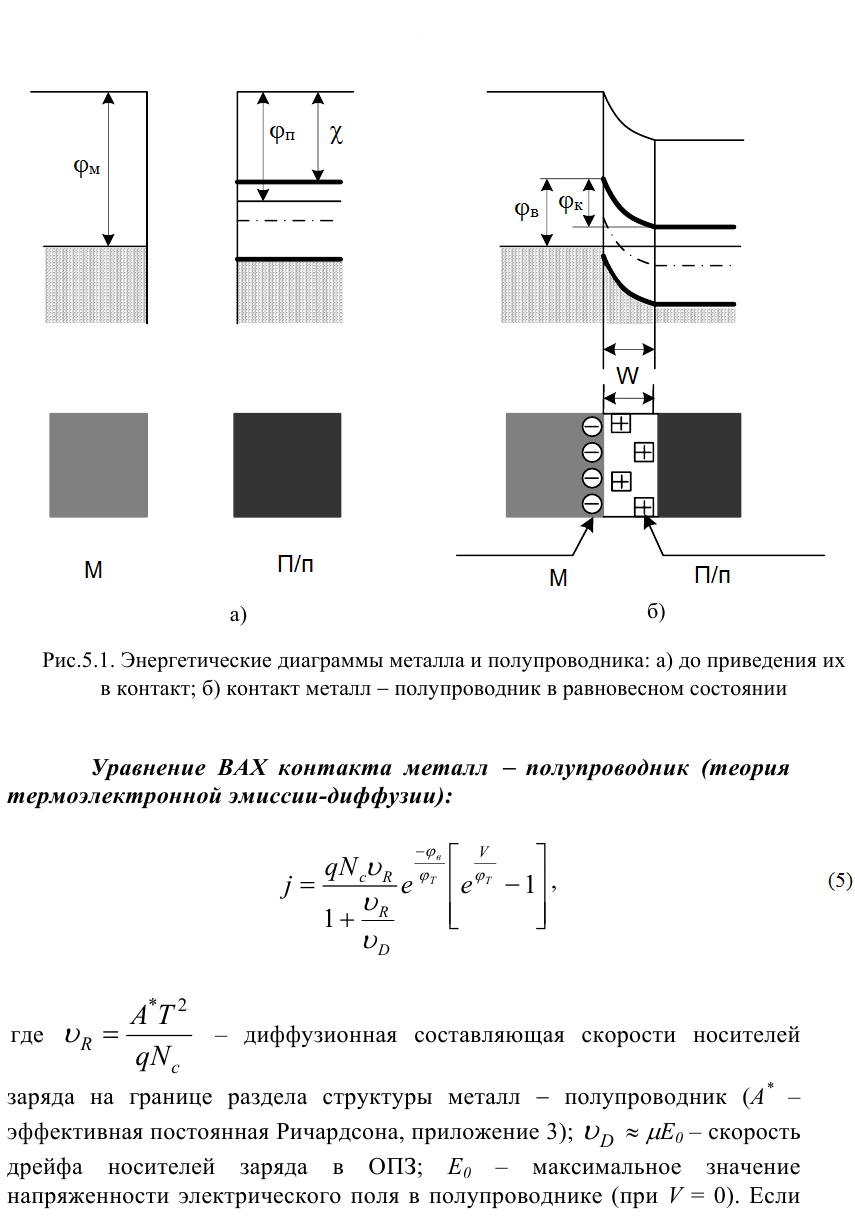 Рисунок 2.1 – Энергетические диаграммы p-n перехода: а) до их приведения в контакт; б) в равновесном состоянии Напряженность электрического поля в ОПЗ полупроводника:  (2.4) (2.4)Уравнение ВАХ контакта металл-полупроводник (теория термоэлектронной эмиссии-диффузии):  (2.5) (2.5)где 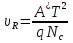 – диффузионная составляющая скорости носителей qNc заряда на границе раздела структуры металл - полупроводник ( – диффузионная составляющая скорости носителей qNc заряда на границе раздела структуры металл - полупроводник ( – эффективная постоянная Ричардсона; – эффективная постоянная Ричардсона;  – скорость дрейфа носителей заряда в ОПЗ; – скорость дрейфа носителей заряда в ОПЗ;  – максимальное значение напряженности электрического поля в полупроводнике (при V = 0). Если – максимальное значение напряженности электрического поля в полупроводнике (при V = 0). Если  , то справедлива теория термоэлектронной эмиссии (теория Бете) и выражение для плотности тока преобразуется к виду: , то справедлива теория термоэлектронной эмиссии (теория Бете) и выражение для плотности тока преобразуется к виду: (2.6) (2.6)В том случае, когда  , определяющим является процесс диффузии (теория Шоттки) и плотность тока вычисляется по формуле: , определяющим является процесс диффузии (теория Шоттки) и плотность тока вычисляется по формуле: (2.7) (2.7)Контактная разность потенциалов р-n-перехода:  (2.8) (2.8)где  – термодинамическая работа выхода электронов из полупроводника p-типа проводимости; – термодинамическая работа выхода электронов из полупроводника p-типа проводимости;  – термодинамическая работа выхода электронов из полупроводника n-типа проводимости (рис.5.2,а); Na, Nd– концентрация акцепторов – термодинамическая работа выхода электронов из полупроводника n-типа проводимости (рис.5.2,а); Na, Nd– концентрация акцепторов и доноров соответственно. Максимальная величина напряженности электрического поля Еmах в р-n-переходе:  (2.9) (2.9)где Wp и Wn– толщина обедненных областей в р- и n-областях р-n-перехода, определяемая соотношениями  (2.10) (2.10)Толщина слоя объемного заряда для резкого р-n-перехода W, равная W= Wp+ Wn:  (2.11) (2.11)Толщина слоя объемного заряда для плавного р-n-перехода:  (2.12) (2.12)где а – градиент концентрации примесей. Плотность тока насыщения (обратного тока) р-n-перехода:  (2.13) (2.13)где  и и  – равновесная концентрации неосновных носителей заряда. – равновесная концентрации неосновных носителей заряда. Рисунок 2.2 – Энергетические диаграммы полупроводников p- и n- типа проводимости: а) до приведения их в контакт; б) p-n-переход в равновесном состоянии Уравнение ВАХ p-n-перехода:  , (2.14) , (2.14)где j– плотность тока, протекающего через р-n-переход при приложении к нему внешнего напряжения смешения V. Величина удельной барьерной емкости резкого р-n-перехода:  (2.15) (2.15)где Nв– концентрация примеси в высокоомной области р-n-перехода. Величина удельной барьерной емкости плавного р-n-перехода:  (2.16) (2.16)Дифференциальное сопротивление р - п-перехода: где  и и  – величины силы тока при прямом и обратном смешениях р-n-перехода соответственно. – величины силы тока при прямом и обратном смешениях р-n-перехода соответственно.Напряжение пробоя резкого несимметричного р-n-перехода:  (2.18) (2.18)Напряжение пробоя линейно-плавного р-n-перехода:  (2.19) (2.19)Барьерная емкость p-n перехода: 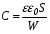 , (2.20) , (2.20)где S – площадь перехода. Диффузионная длина носителей заряда Ln,p выражается формулой 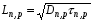 , (2.21) , (2.21)где Dn,p – коэффициенты диффузии носителей; τn,p – время жизни носителей. Соотношения Энштейна:  , (2.22) , (2.22)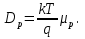 (2.23) (2.23)Если 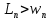 , ,  , обратный ток необходимо вычислить по формуле: , обратный ток необходимо вычислить по формуле: . (2.24) . (2.24)2 Расчётное задание. Вариант№2.
1.Рассчитать контактную разность потенциалов на p-n-переходе. Чтобы найти контактную разность потенциалов, воспользуемся формулой (2.8):  Решение:  Ответ: 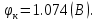 2.Рассчитать полную ширину d запирающего (обеднённого зарядами) слоя p-n-перехода, а также ширину частей этого слоя в р- и n-областях перехода. Решение: Чтобы вычислить ширину частей этого слоя в р- и n-областях перехода, можно воспользоваться формулой (2.10).   , ,  Чтобы вычислить ширину p-n-перехода, можно воспользоваться формулой (2.11). 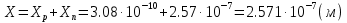 Ответ.  ; ;  3. Рассчитать и построить распределение напряжённости электрического поля в запирающем слое p-n-перехода вдоль оси Х, направленной слева на право от области р к области n перехода. Определить максимальное значение напряжённости электрического поля в переходе. Решение: Чтобы определить максимальное значение напряжённости электрического поля в переходе, воспользуемся формулой (2.9):  (В/м). (В/м).Чтобы рассчитать и построить распределение напряжённости электрического поля в запирающем слое p-n-перехода вдоль оси Х, направленной слева на право от области р к области n перехода, воспользуемся расчетными данными из 2 задания Eet=Ee=-  -Xp =  Xn=  Emax=  (В/м) (В/м)  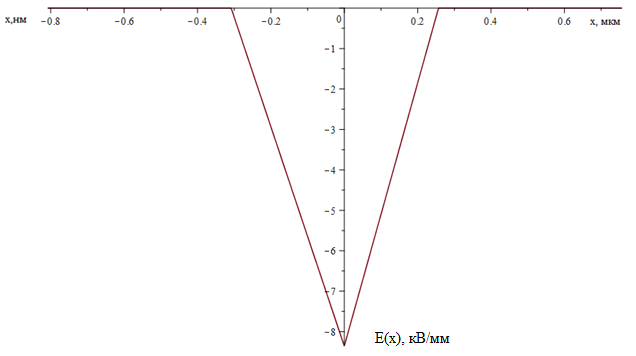 Ответ: 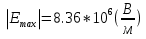 4. Рассчитать и построить распределение потенциала электрического поля в запирающем слое p-n-перехода вдоль оси Х, направленной слева на право от области р к области n перехода. Принять значение потенциала в р-области вдали от перехода равным φр = 0. Решение:  Из условия дано φр = 0, следовательно, φk= φn. Зная φn выражения принимают следующий вид:    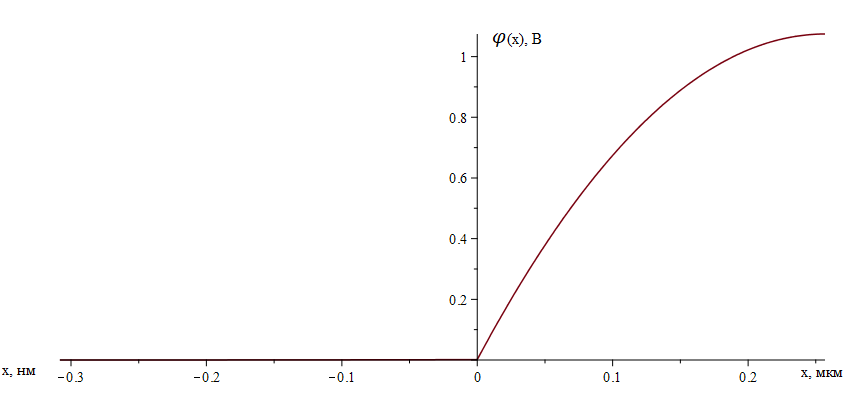 5.Рассчитать обратный ток насыщения I0 через p-n-переход. На основании полученного значения I0 рассчитать и построить вольт-амперную характеристику идеального p-n-перехода для значений напряжения на переходе, лежащих в диапазоне: -10 В ≤ U ≤ 2 В. Решение: Воспользуемся формулой :  , , Примем концентрации основных носителей заряда: 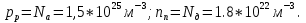 Концентрации неосновных носителей заряда выразим из закона действующих масс (1): 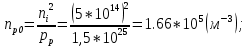  Чтобы найти Ln,Lp воспользуемся формулой 2.21:   ; ;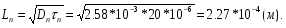 Чтобы найти Dn,Dp воспользуемся соотношением:    Уравнение ВАХ p-n-перехода:  . . Пример расчётов: при 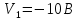 : : при  : :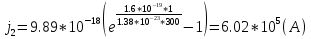  Ответ: I0=  (А). (А).6.Рассчитать и построить зависимости барьерной и диффузионной ёмкостей p-n-перехода от значения приложенного к переходу напряжения. Для расчета диффузионной емкость используем формулу:  , ,При U=0.7(В): 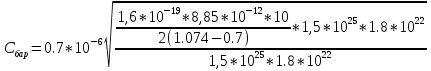 Для барьерной ёмкости следует использовать напряжения из диапазона: -10 В ≤ U ≤ (φк – 0,1) В.  Рисунок 4 – Вольт-фарадная характеристика перехода Расчёт и построение зависимости диффузионной ёмкости p-n-перехода от значения приложенного к переходу напряжения производиться по полной формуле (2.8) [3]:
где
Тогда при значении напряжения U=1 В значения  , ,  равны: равны:
Из формулы (2.8) [3]:
Из формулы (3.2) выводим следующее [3]:
где
Тогда при значении напряжения U=0.7 В значения  , , 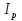 равны: равны:
Однако, если в p-n-переходе ток инжекции электронов  и ток инжекции дырок и ток инжекции дырок 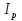 различаются на два и более порядков, можно использовать упрощенную формулу диффузионной емкости. При этом необходимо использовать значение тока, величина которого больше. Меньшим же значением можно пренебречь. В данном случае ток инжекции дырок больше, поэтому упрощенная формула имеет вид [3]: различаются на два и более порядков, можно использовать упрощенную формулу диффузионной емкости. При этом необходимо использовать значение тока, величина которого больше. Меньшим же значением можно пренебречь. В данном случае ток инжекции дырок больше, поэтому упрощенная формула имеет вид [3]:
Для диффузионной ёмкости следует использовать напряжения из диапазона: 0 B ≤ U ≤ U*, где U* - прямое напряжение на p-n-переходе, соответствующее току через переход I = 1 А. 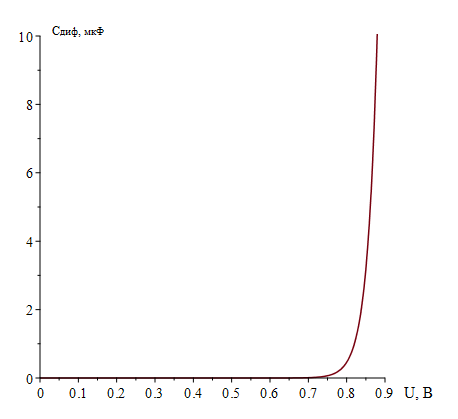 Рисунок 5 - Зависимость диффузионной ёмкости p-n-перехода от значения приложенного к переходу напряжения 7. Для вычисления статического сопротивления необходимо рассчитать значения тока, используя заданное значение сопротивления c помощью формулы (2.6):  Вычисление статическое сопротивление p-n-перехода для значения прямого внешнего напряжения на переходе UВ производиться по формуле [1]:
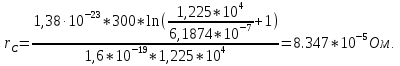 Вычисление дифференциального сопротивления p-n-перехода производиться по формуле [1]:
 Ответ: rc =  rd = rd =  ВЫВОД: При выполнении работы была освоена методика расчёта энергетических параметров контактов металлов и полупроводников, таких как контактная разность потенциалов, обратный ток насыщения и его плотность, диффузионная и барьерную ёмкость p-n перехода. Также в расчетах был обоснован выбор выражения для расчета вольтамперной характеристики p-n перехода 30 Лабораторная работа № 2 Окорочков А.И. ИСОиП (филиал) ДГТУ Кафедра РЭСиК Разраб. Провер. 3.3 Реализация задачи Н.контр. Утв. Лит Лист Изм Подпись Дата Лист Листов 15 ФОМЭ.030000.000 ЛР № докум. |


 .
.
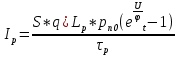 ,
,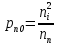 ,
,



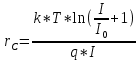 ,
, ,
,