методичка имитационное моделирование. 1 Основные понятия теории массового обслуживания
 Скачать 0.52 Mb.
|
|
Пример 1: Салон-парикмахерская имеет 5 мастеров. В час пик интенсивность потока клиентов равна 6 человек. В час. Обслуживание одного клиента длится в среднем 40 минут. Определить среднюю длину очереди, считая ее неограниченной. Фрагмент решения задачи в Mathcad. 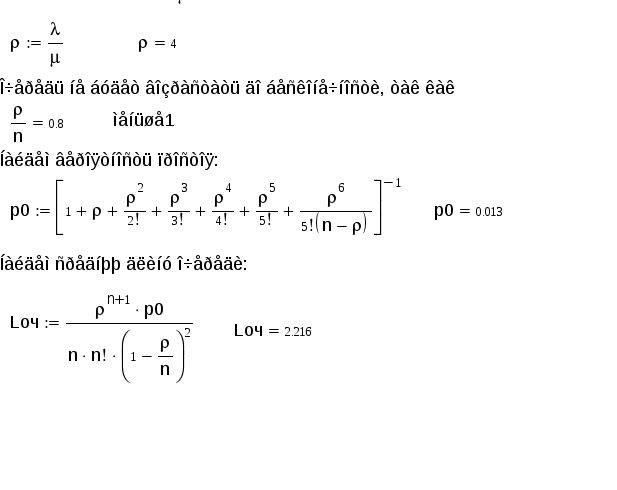 Пример 2: В железнодорожной кассе имеются 2 окна. Время на обслуживания одного пассажира 0,5 минут. Пассажиры подходят к кассе по 3 человека. Определить все характеристики системы. Фрагмент решения задачи в Mathcad. 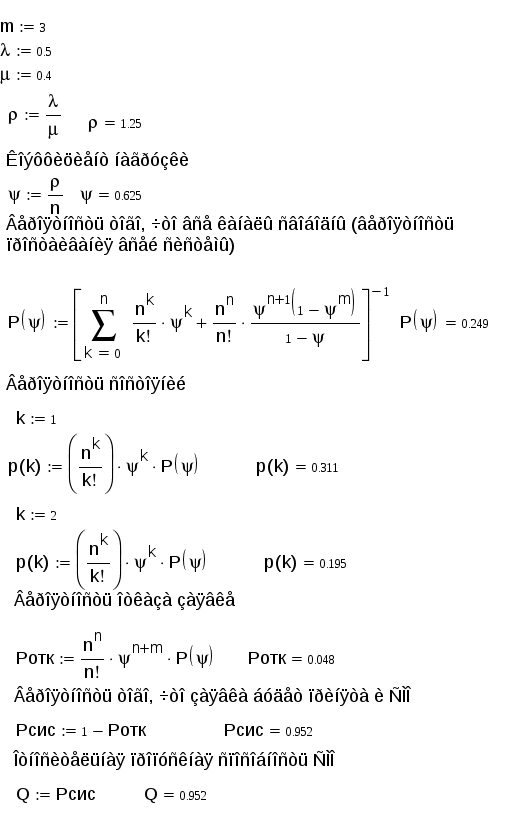 Продолжение решения задачи в Mathcad.  7 Многоканальная СМО с ограниченной очередью Расчеты основных показателей функционирования системы, имеющей nканалов обслуживания, с ограничением мест в очереди, проводятся аналогично тем, которые были сделаны для системы с неограниченной очередью. Особенностью функционирования систем с ограничением длины очереди является конечное число состояний системы. Пусть на каналы обслуживания поступает простейший поток требований интенсивностью λ. Поток обслуживания, поступающий с одного канала, также простейший и имеет интенсивность μ. Число мест в очереди ограничено и равно т. По числу заявок, находящихся в системе, обозначим состояния системы: S0 - состояние простоя; ………. Sп - состояние системы, когда все каналы заняты обслуживанием; Sп+1 - все каналы заняты, одна заявка находится в очереди; Sп+т - в очереди т заявок. Так как потоки заявок и обслуживания ординарны, граф состояний изображается в виде схемы гибели и размножения. Отличие от подобной схемы для неограниченной очереди состоит только в том, что число состояний конечно. Граф состояний такой системы изображается в виде схемы на рисунке номер 7: λ λ λ λ λ λ     ……. ……. S0 S1 S2 Sn Sn+m   μ 2μ 3μ ………. nμ nμ …… nμ Рисунок 7: Многоканальная СМО с ограниченной очередью. Составим систему алгебраических уравнений для нахождения финальных вероятностей состояний: 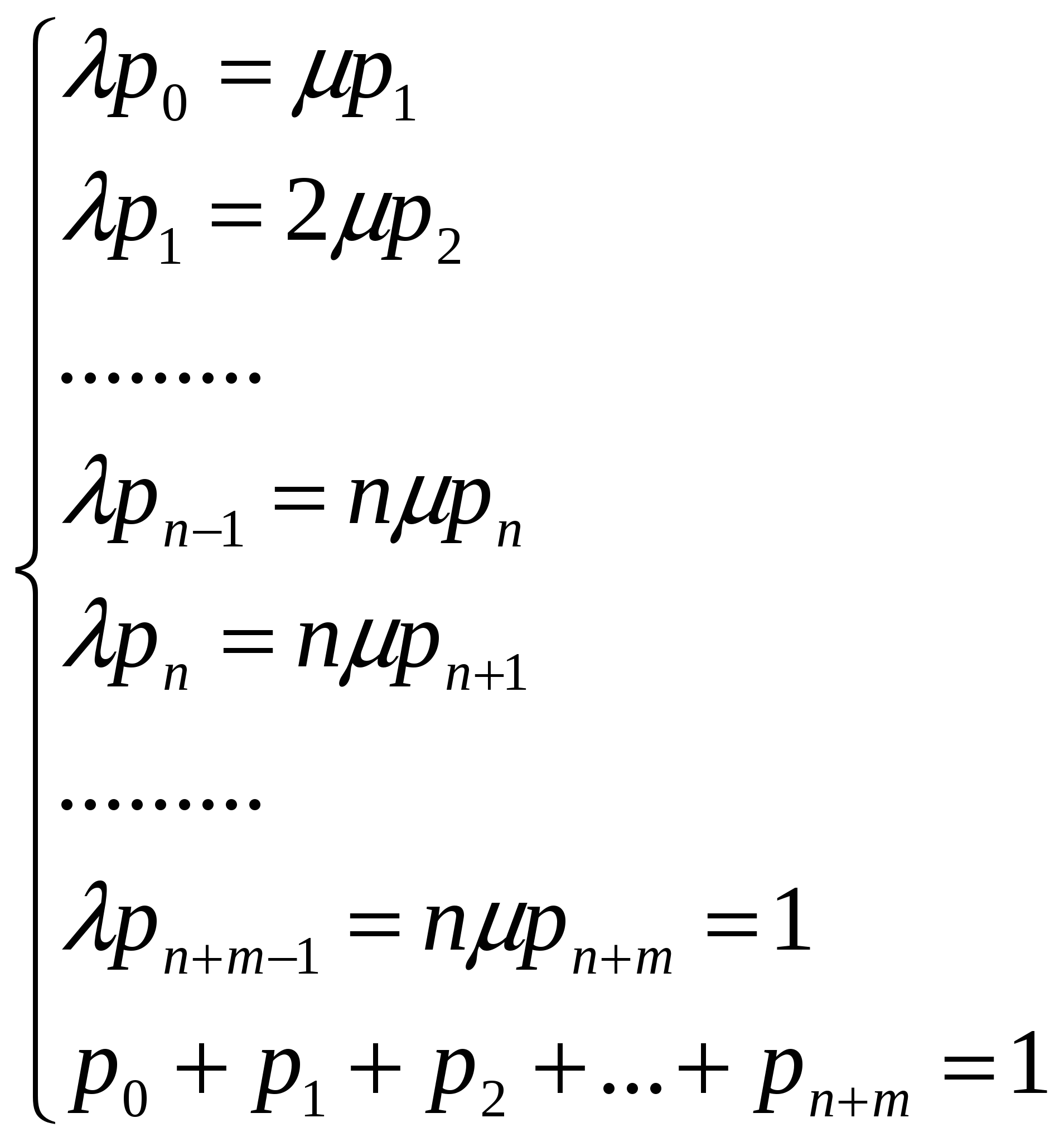 (80)Откуда получим формулы Эрланга для многоканальной системы с ограниченной очередью:  (81)Последние т слагаемых в скобках представляют собой сумму т первых членов геометрической прогрессии со знаменателем ρ/n которая равна : 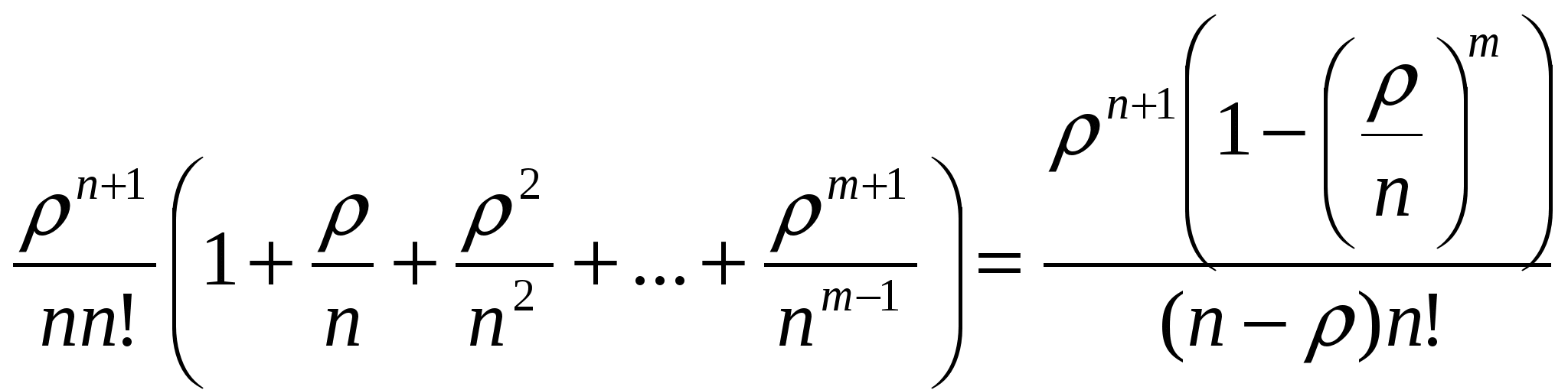 (82)Таким образом, для вычисления р0 получим формулу: 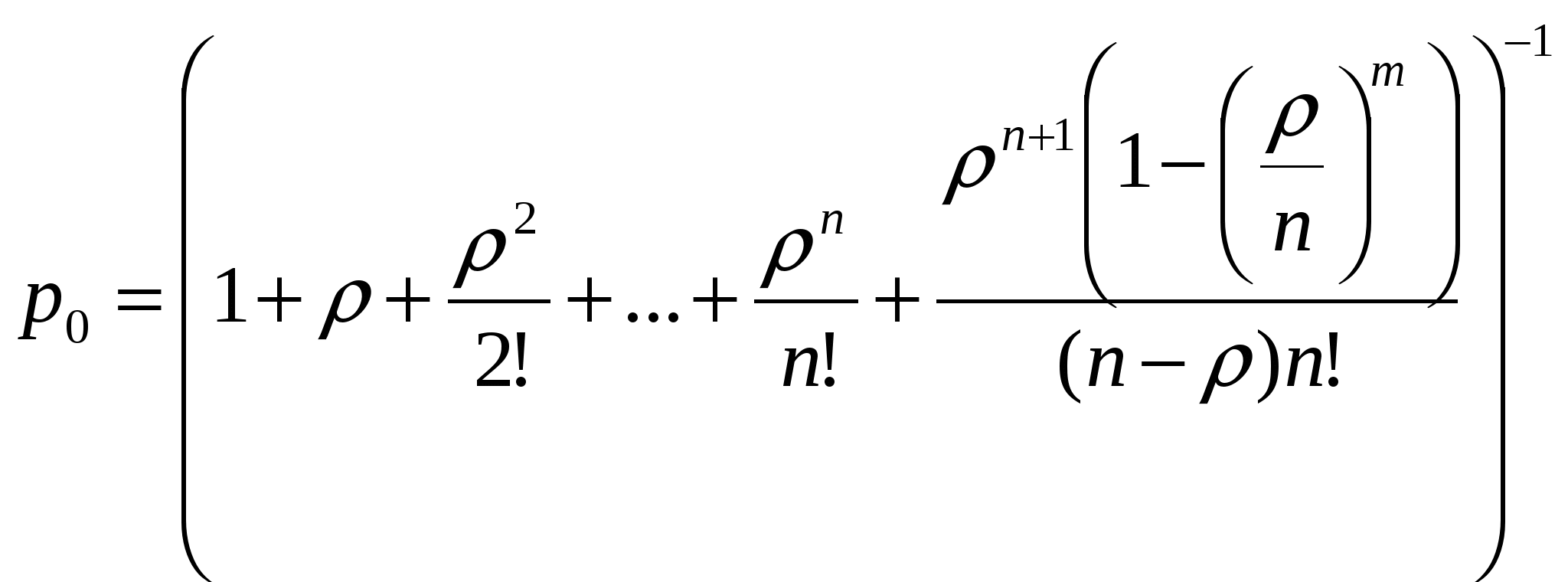 (83)Формулы для вероятностей предельных состояний будут иметь вид:  (84)Приведем формулы для расчета основных показателей эффективности работы системы. Число каналов, которые необходимо иметь, чтобы система справлялась с потоком заявок, определим из условия  (85)В этом случае выполняется соотношение ρ < 1. Вероятность отказа в обслуживании заявки определим как вероятность того, что при поступлении заявки в систему все nее каналов будут заняты, и в очереди заняты все mмест:  (86)Отсюда вероятность обслуживания (а также и относительная пропускная способность системы) равны вероятности противоположного события:  (87)Абсолютная пропускная способность - число заявок, обслуженных системой в единицу времени:  (88)Так как каждый канал обслуживает μзаявок в единицу времени, то среднее число занятых каналов можно вычислить:  (89)Среднее время обслуживания каналом одной заявки:  (90)Среднее число заявок в очереди: 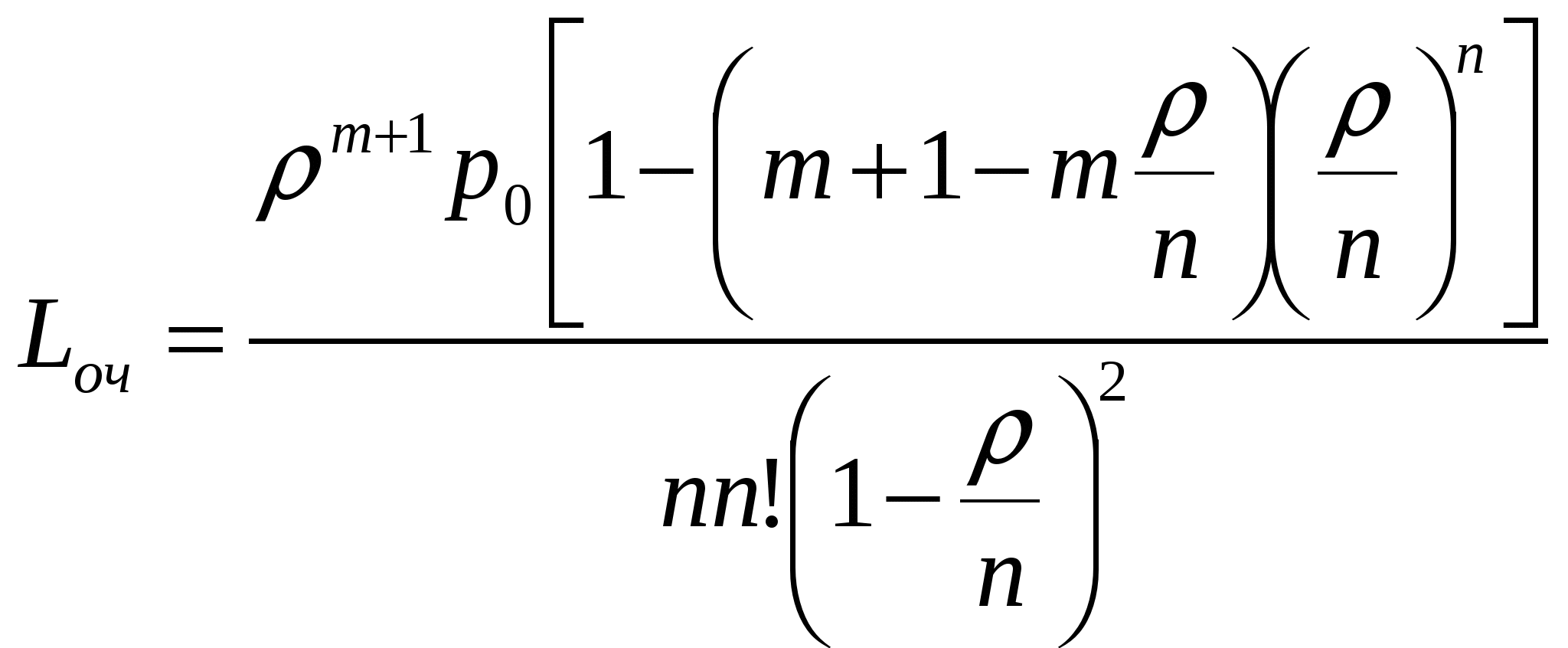 (91)Среднее число заявок под обслуживанием равно среднему числу занятых каналов:  (92)Среднее число заявок в системе (под обслуживанием и в очереди) равно:  (93)Многоканальную СМО с ограниченной очередью можно рассмотреть в Mathcad. Пример: Площадка АЗС вмещает не более 3-х машин одновременно, и если она занята, то очередная машина, прибывшая к станции, в очередь не становится. Интенсивность потока обслуживания λ=0,5 машин в минуту. Интенсивность потока обслуживания μ=0,4 машины в минуту. Определить все характеристики СМО. Фрагмент решения задачи в Mathcad. 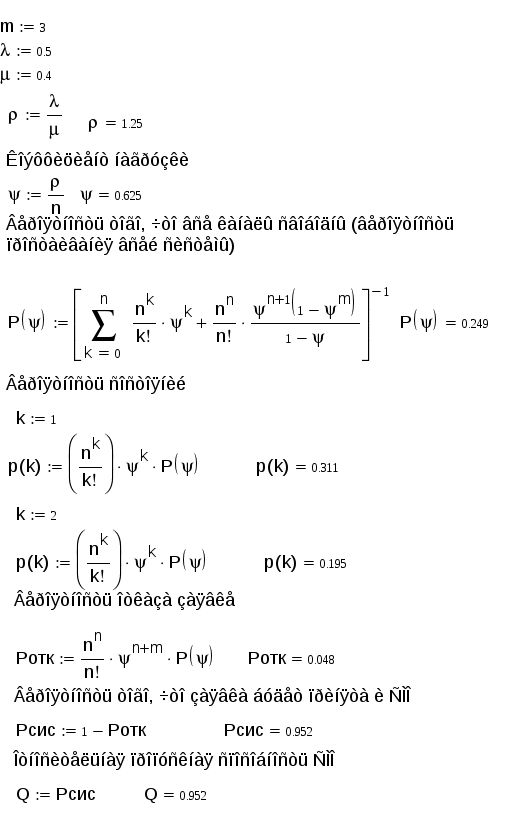 Продолжение задачи в Mathcad. Заключение Многие экономические задачи связаны с системами массового обслуживания (СМО), т. е. такими системами, в которых, с одной стороны, возникают массовые запросы (требования) на выполнение каких-либо услуг, с другой — происходит удовлетворение этих запросов. СМО включает в себя следующие элементы: источник требований, входящий поток требований, очередь, обслуживающие устройства (каналы обслуживания), выходящий поток требований. Исследованием таких систем занимается теория массового обслуживания. Методами теории массового обслуживания могут быть решены многие задачи исследования процессов, происходящих в экономике. Так, в организации торговли эти методы позволяют определить оптимальное количество торговых точек данного профиля, численность продавцов, частоту завоза товаров и другие параметры. Другим характерным примером систем массового обслуживания могут служить склады или базы снабженческо-сбытовых организаций, и задача теории массового обслуживания в данном случае сводится к тому, чтобы установить оптимальное соотношение между числом поступающих на базу требований на обслуживание и числом обслуживающих устройств, при котором суммарные расходы на обслуживание и убытки от простоя транспорта были бы минимальными. Теория массового обслуживания может найти применение и при расчете площади складских помещений, при этом складская площадь рассматривается как обслуживающее устройство, а прибытие транспортных средств под выгрузку — как требование. Модели теории массового обслуживания применяются также при решении ряда задач организации и нормирования труда, других социально-экономических проблем. В работе рассматривались такие СМО, как: - Одноканальная СМО с отказами; - Многоканальная СМО с отказами; - Одноканальная СМО с ожиданием; - Одноканальная СМО с ограниченной очередью; - Многоканальная СМО с неограниченной очередью; - Многоканальная СМО с ограниченной очередью. Предметом теории СМО является построение математических моделей (т. е. образов реального экономического объекта, описанных с помощью уравнений, формул, графиков, схем и т. д.) для теоретического анализа и практического использования свойств СМО. Эффективность функционирования СМО описывается такими показателями: 1) Эффективность использования СМО; 2) Качество обслуживания. По дисциплине обслуживания: — СМО с отказами; — СМО с ожиданием (очередью); — Системы с ограничением длины очереди; — Системы с ограниченным временем ожидания; По месту нахождения источника требований: — Замкнутые СМО; — Открытые СМО; По числу обслуживающих каналов: — Одноканальные; — Многоканальные. Задачи для самостоятельного решения Задача 1 Одноканальная СМО с отказами представляет собой одну телефонную линию. Заявка (вызов), пришедшая в момент, когда линия занята, получает отказ. Все потоки событий простейшие. Интенсивность потока  = 0,95 вызова в минуту. Средняя продолжительность разговора  =1 мин. Определите вероятностные характеристики СМО в установившемся режиме работы.Задача 2 В одноканальную СМО с отказами поступает простейший поток заявок с интенсивностью = 0,5 заявки в минуту. Время обслуживания заявки имеет показательное распределение с =1,5 мин. Определите вероятностные характеристики СМО в установившемся режиме работы.Задача 3 В вычислительном центре работает 5 персональных компьютеров (ПК). Простейший поток задач, поступающих на ВЦ, имеет интенсивность = 10 задач в час. Среднее время решения задачи равно 12 мин. Заявка получает отказ, если все ПК заняты. Найдите вероятностные характеристики системы обслуживания (ВЦ).Задача 4 В аудиторскую фирму поступает простейший поток заявок на обслуживание с интенсивностью = 1,5 заявки в день. Время обслуживания распределено по показательному закону и равно в среднем трем дням. Аудиторская фирма располагает пятью независимыми бухгалтерами, выполняющими аудиторские проверки (обслуживание заявок). Очередь заявок не ограничена. Дисциплина очереди не регламентирована. Определите вероятностные характеристики аудиторской фирмы как системы массового обслуживания, работающей в стационарном режиме.Задача 5 На пункт техосмотра поступает простейший поток заявок (автомобилей) интенсивности = 4 машины в час. Время осмотра распределено по показательному закону и равно в среднем 17 мин., в очереди может находиться не более 5 автомобилей. Определите вероятностные характеристики пункта техосмотра в установившемся режиме.Задача 6 На промышленном предприятии решается вопрос о том, сколько потребуется механиков для работы в ремонтном цехе. Пусть предприятие имеет 10 машин, требующих ремонта с учетом числа ремонтирующихся. Отказы машин происходят с частотой = 10 отк/час. Для устранения неисправности механику требуется в среднем = 3 мин. Распределение моментов возникновения отказов является пуассоновским, а продолжительность выполнения ремонтных работ распределена экспоненциально. Возможно организовать 4 или 6 рабочих мест в цехе для механиков предприятия. Необходимо выбрать наиболее эффективный вариант обеспечения ремонтного цеха рабочими местами для механиков.Задача 7 В бухгалтерии предприятия имеются два кассира, каждый из которых может обслужить в среднем 30 сотрудников в час. Поток сотрудников, получающих заработную плату, - простейший, с интенсивностью, равной 40 сотрудников в час. Очередь в кассе не ограничена. Дисциплина очереди не регламентирована. Время обслуживания подчинено экспоненциальному закону распределения. Вычислите вероятностные характеристики СМО в стационарном режиме и определите целесообразность приема третьего кассира на предприятие, работающего с такой же производительностью, как и первые два. Задача 8 В инструментальном отделении сборочного цеха работают три кладовщика. В среднем за 1 мин. за инструментом приходят 0,8 рабочего ( = 0,8). Обслуживание одного рабочего занимает у кладовщика = 1,0 мин. Очередь не имеет ограничения. Известно, что поток рабочих за инструментом - пуассоновский, а время обслуживания подчинено экспоненциальному закону распределения. Стоимость 1 мин. работы рабочего равна 30 д. е., а кладовщика - 15 д. е. Найдите средние потери цеха при данной организации обслуживания в инструментальном отделении (стоимость простоя) при стационарном режиме работы.Задача 9 Билетная касса работает без перерыва. Билеты продает один кассир. Среднее время обслуживания - 2 мин. на каждого человека. Среднее число пассажиров, желающих приобрести билеты в кассе в течение одного часа, равно = 20 пасс/час. Все потоки в системе простейшие. Определите среднюю длину очереди, вероятность простоя кассира, среднее время нахождения пассажира в билетной кассе (в очереди и на обслуживании), среднее время ожидания в очереди в условиях стационарного режима работы кассы.Задача 10 Пост диагностики автомобилей представляет собой одноканальную СМО с отказами. Заявка на диагностику, поступившая в момент, когда пост занят, получает отказ. Интенсивность потока заявок на диагностику = 0,5 автомобиля в час. Средняя продолжительность диагностики = 1,2 часа. Все потоки событий в системе простейшие. Определите в установившемся режиме вероятностные характеристики системы.Задача 11 Автозаправочная станция представляет собой СМО с одним каналом обслуживания и одной колонкой. Площадка при АЗС допускает пребывание в очереди на заправку не более трех автомобилей одновременно. Если в очереди уже находится три автомобиля, очередной автомобиль, прибывший к станции, в очередь не становится, а проезжает мимо. Поток автомобилей, прибывающих для заправки, имеет интенсивность = 0,7 автомобиля в минуту. Процесс заправки продолжается в среднем 1,25 мин. Все потоки простейшие. Определите вероятностные характеристики СМО в стационарном режиме.Задача 12 На железнодорожную сортировочную горку прибывают составы с интенсивностью = 2 состава в час. Среднее время, в течение которого горка обслуживает состав, равно 0,4 час. Составы, прибывающие в момент, когда горка занята, становятся в очередь и ожидают в парке прибытия, где имеется три запасных пути, на каждом из которых может ожидать один состав. Состав, прибывший в момент, когда все три запасных пути в парке прибытия заняты, становится в очередь на внешний путь. Все потоки событий простейшие.При установившемся режиме найдите: среднее число составов, ожидающих в очереди (как в парке прибытия, так и вне его); среднее время ожидания в парке прибытия и на внешних путях; среднее время ожидания состава в системе обслуживания; вероятность того, что прибывший состав займет место на внешних путях. Задача 13 Рассматривается работа АЗС, на которой имеется три заправочные колонки. Заправка одной машины длится в среднем 3 мин. В среднем на АЗС каждую минуту прибывает машина, нуждающаяся в заправке бензином. Число мест в очереди не ограничено. Все машины, вставшие в очередь на заправку, дожидаются своей очереди. Все потоки в системе простейшие. Определите вероятностные характеристики работы АЗС в стационарном режиме. |