методичка имитационное моделирование. 1 Основные понятия теории массового обслуживания

• Название: 1 Основные понятия теории массового обслуживания
• Анкор: методичка имитационное моделирование.doc
• Дата: 07.05.2017
• Размер: 0.52 Mb.
• Имя файла: методичка имитационное моделирование.doc
• Тип: Реферат; #7188
• страница: 2 из 4

Пример:

Заявки на телефонные переговоры в переговорный пункт поступают с интенсивностью 90 заявок в час. Считая среднюю продолжительность разговора равной 3 минутам, определить оптимальное число телефонных номеров, чтобы 90% всех заявок на переговоры были удовлетворены.

Фрагмент решения задачи в Mathcad.



4 Одноканальная СМО с ожиданием
Рассмотрим функционирование одноканальной системы S, в которую поступает простейший поток требований интенсивностью λ. Интенсивность потока обслуживания равна μ.

По числу заявок, находящихся в системе, обозначим состояния системы: S₀,S₁,S₂,…,S_k,…S_n , где S_k – состояние системы, когда в ней находится k заявок (одна обслуживается, остальные k-1 стоят в очереди). Никаких ограничений на длину очереди нет. Примерами таких систем может служить телефон-автомат, кассир в магазине, железнодорожная касса и т.д. Так как поток заявок и обслуживания ординарен, и число состояний системы бесконечно, граф состояний такой системы изображается в виде схемы гибели и размножения на рисунке номер 4:

λ λ λ λ λ

……. .…..

S₀ S₁ S₂ S_k

μ μ μ ^………. μ μ ^……..
Рисунок 4: Одноканальная СМО с ожиданием.

Интенсивность μ, потока обслуживаний не меняется при переходе из состояния S_k в состояние S_k-1 и обратна по величине среднему времени обслуживания заявки:

(33)

Финальные вероятности состояний такой системы существуют только в случае, если выполнено условие ρ < 1 , так как в этом случае очередь не будет расти до бесконечности.

Уравнение для нахождения р₀получим аналогично тому как это было сделано для одноканальной системы с отказами:

(34)
С учетом формулы

, (35)

получим

(36)

где ρ – показатель нагрузки канала обслуживания.

Так как при ρ < 1 предельные вероятности существуют, то выражении ев скобках представляет собой сумму бесконечного числа членов убывающей геометрической прогрессии, предел которого равен:

(37)

откуда

(38)

Фрмула для вероятностей предельных состояний будут иметь вид:

, , ……. ,, … (39)

Предельные вероятности состояний S_k также образуют убывающуб геометрическую прогрессию, поэтому наиболее высокой будет вероятность р₀, то есть вероятность простоя системы и готовности принять заявку к обслуживанию.

Формулы для расчета основных показателей эффективности работы системы.

Вероятность отказа в обслуживании заявки при условии неограниченности очереди равна нулю, так как все заявки в конце концов будут обслужены. Отсюда вероятность обслуживания (а также и относительная пропускная способность системы) равна единице:

. (40)

Абсолютная пропускная способность равна интенсивности входящего потока, так как обслуживаются все заявки:

(41)

Среднее время обслуживания каналом одной заявки:

(42)

Так как вероятность того, что в системе находится kзаявок, равна р_k, среднее число заявок в системе определим как математическое ожидание числа заявок в системе (под обслуживанием и в очереди ):

(43)
Подставив в формулу выражение для р_k , получим:

(44)

При ρ < 1 такой ряд сходится, что можно проверить, воспользовавшись каким-либо признаком сходимости числовых рядов.

Заметим, что kρ^k - это производная по ρ функции ρ^k .

Применив правило вычисления производной суммы, поменяем местами знак суммы и знаки дифференцирования:

(45)

Но теперь под знаком суммы находится убывающая геометрическая прогрессия со знаменателем, меньшим единицы. Поэтому

(46)

Среднее число заявок под обслуживанием L_обнайдем как математическое ожидание числа обслуживаемых заявок. Это либо 0 заявок, когда канал свободен, либо 1 заявка, когда канал занят:

(47)

Отсюда видно, что среднее число заявок под обслуживанием равно вероятности того, что канал занят:

(48)

Очевидно, среднее число заявок в очереди равно разности между числом заявок в системе и числом обслуживаемых заявок:

(49)

Среднее время пребывания заявки в системе (или в очереди) можно найти по формулам Литтла, разделив среднее число заявок в системе (в очереди) на интенсивность потока заявок:

(50)

(51)

Формулы Литтла основаны на том, что если система справляется с потоком заявок, то интенсивности входящего и выходящего потока заявок равны, то есть обслуживаются все заявки, поступающие в систему.

Одноканальную СМО с ожиданием можно рассмотреть в Mathcad.

Пример:

Железнодорожная касса обслуживает по одному человеку. Интенсивность потока пассажиров 0,45. Среднее время обслуживания одной заявки 2 минуты. Найти все предельные характеристики

эффективности функционирования одноканальной СМО с ожиданиями.

Фрагмент решения задачи в Mathcad.



5 Одноканальная СМО с ограниченной очередью
В систему поступает пуассоновский поток требований интенсивностью λ, поток обслуживания имеет интенсивность μ, максимальное число мест в очереди – т . Если заявка поступает в систему, когда все места в очереди заняты, она покидает систему необслуженной.

Финальные вероятности состояний такой системы всегда существуют, так как число состояний конечно:

S₀ – система свободна и находится в состоянии простоя;

S₁ – обслуживается одна заявка, канал занят, очереди нет;

S₂ – одна заявка обслуживается, одна в очереди;

…

S_m+1- одна заявка обслуживается, т в очереди.

Граф состояний такой системы показан на рисунке номер 5:

λ λ λ λ λ

…….

S₀ S₁ S₂ S_m+1

μ μ μ ^………. μ μ

Рисунок 5: Одноканальная СМО с ограниченной очередью.
В формуле для р₀найдем сумму конечного числа членов геометрической прогрессии:

(52)

С учетом формулы для ρ получим выражение:

(53)

В скобках находится (m+2) элементов геометрической прогрессии с первым членом 1 и знаменателем ρ. По формуле суммы (m+2) членов прогрессии:

(54)

Отсюда

(55)

Формулы для вероятностей предельных состояний будут иметь вид:

(56)

Вероятность отказа в обслуживании заявки определим как вероятность того, что при поступлении заявки в систему ее канал будет занят и все места в очереди также заняты:

(57)

Отсюда вероятность обслуживания (а также и относительная пропускная способность) равны вероятности противоположного события:

(58)

Абсолютная пропускная способность – число заявок, обслуженных системой в единицу времени:

(59)

Среднее число заявок под обслуживанием:

(60)

Среднее число заявок в очереди:

(61)

Среднее число заявок в системе:

(62)

Одноканальную СМО с ограниченной очередью можно рассмотреть в Mathcad.

Пример:

На стоянке обслуживается 3 машины с интенсивностью потока 0,5 и средним временем обслуживания 2,5 минуты. Определить все показатели системы.


Фрагмент решения задачи в Mathcad.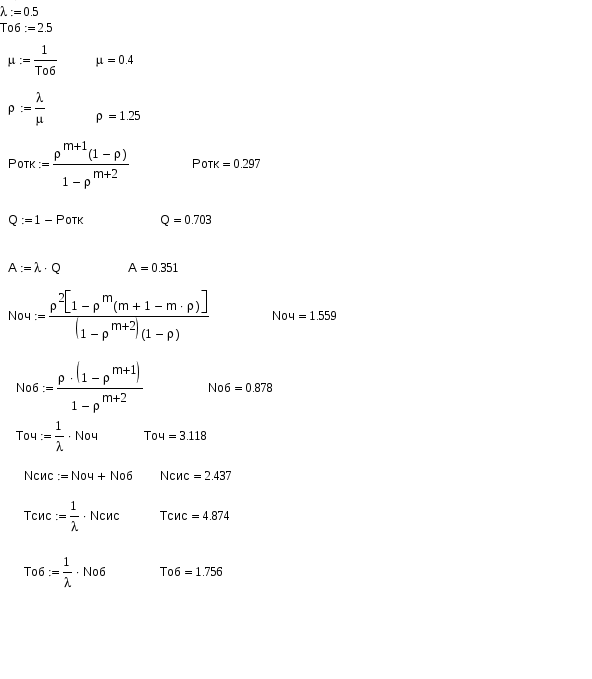



6 Многоканальная СМО с неограниченной очередью
Пусть дана система S, имеющая п каналов обслуживания, на которые поступает простейший поток требований интенсивностью λ. Пусть поток обслуживания также простейший и имеет интенсивность μ. Очередь на обслуживание не ограничена.

По числу заявок, находящихся в системе, обозначим состояния системы: S₀,S₁,S₂,…,S_k,…S_n , где S_k – состояние системы, когда в ней находится k заявок (максимальное число заявок под обслуживанием - n). Граф состояний такой системы изображается в виде схемы на рисунке номер 6:

λ λ λ λ λ λ λ

……. …….

S₀ S₁ S₂ S_m+1 S_n

μ 2μ 3μ ^………. kμ (k+1)μ ^…… nμ nμ
Рисунок 6: Многоканальная СМО с неограниченной очередью.
Интенсивность потока обслуживаний меняется в зависимости от состояния системы: kμпри переходе из состояния S_kв состояние S_k-1 так как может освободиться любой из kканалов; после того, как все каналы заняты обслуживанием, интенсивность потока обслуживаний остается равной пμ, при поступлении в систему следующих заявок.

Для нахождения финальных вероятностей состояний получим формулы аналогично тому, как это было сделано для одноканальной системы.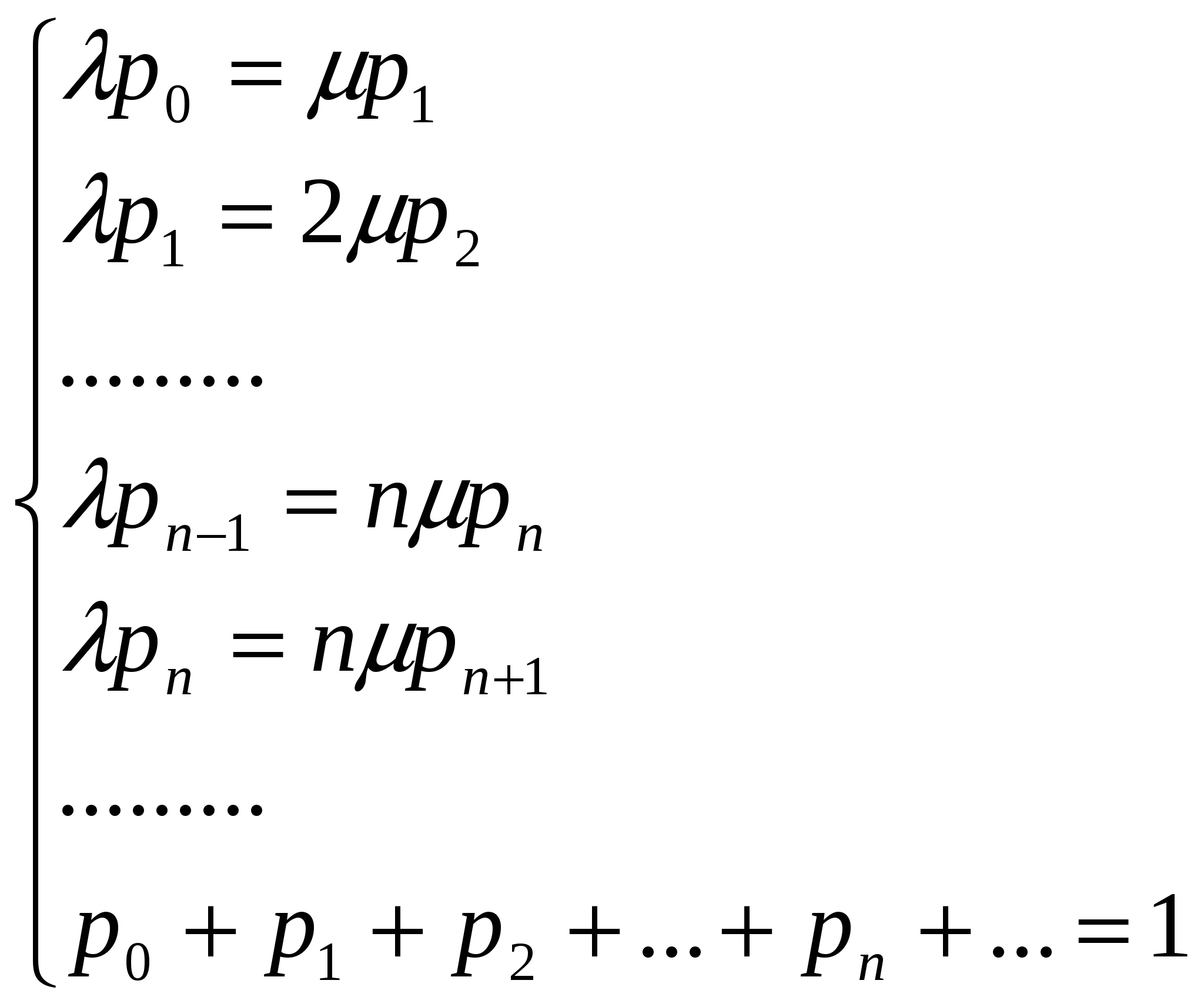

(63)

Отсюда формулы для финальных вероятностей выражаются через

(64)

Для нахождения р₀получим уравнение:

(65)

Для слагаемых в скобках, начиная с (n + 2)-го, можно применить формулу нахождения суммы бесконечно убывающей геометрической прогрессии с первым членом 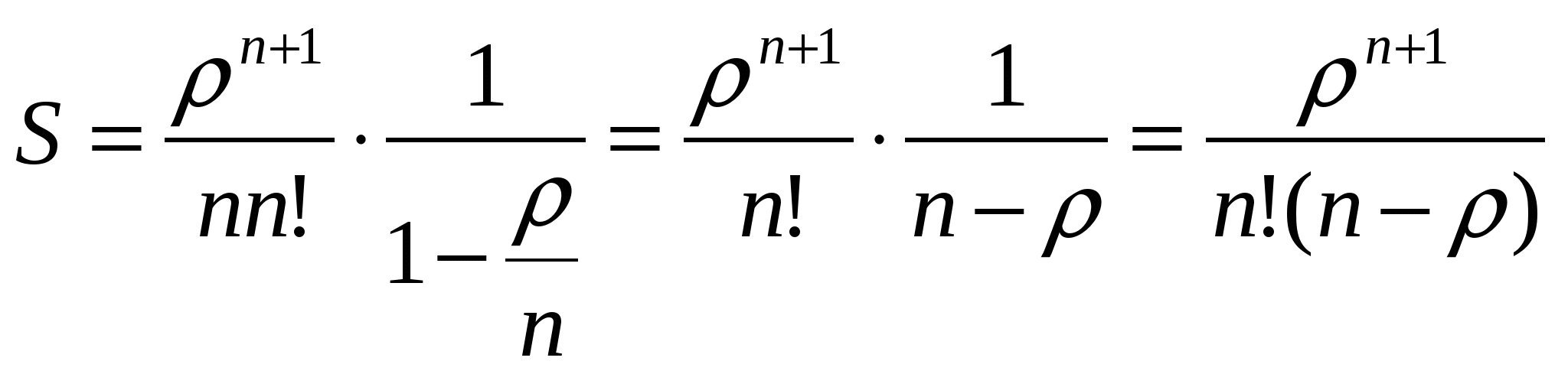и знаменателем ρ/n:

(66)

Окончательно получим формулу Эрланга для нахождения вероятности простоя системы:

(67)

Приведем формулы для расчета основных яоказателей эффективности работы системы.

Система будет справляться с потоком заявок, если

выполнено условие

, (68)

которое означает, что число заявок, поступивших в систему за единицу времени, не превосходит числа заявок, обслуженных системой за это же время. При этом вероятность отказа в обслуживании равна нулю.

Отсюда вероятность обслуживания (а также и относительная пропускная способность системы) равны вероятности противоположного события, то есть единице:

(69)

Абсолютная пропускная способность - число заявок, обслуженных системой в единицу времени:

(70)

Если система справляется с потоком заявок, то в стационарном режиме интенсивность выходящего потока равна интенсивности потока поступающих в систему заявок, так как обслуживаются все заявки:

ν=λ. (71)

Так как каждый канал обслуживает μ заявок в единицу времени, то среднее число занятых каналов можно вычислить:

(72)

Среднее время обслуживания каналом одной заявки;

. (73)

Вероятность того, что при поступлении в систему заявка окажется в очереди, равна вероятности того, что в системе находится более чем п заявок:

(74)

Число заявок, находящихся под обслуживанием, равно числу занятых каналов:

(75)

Среднее число заявок в очереди: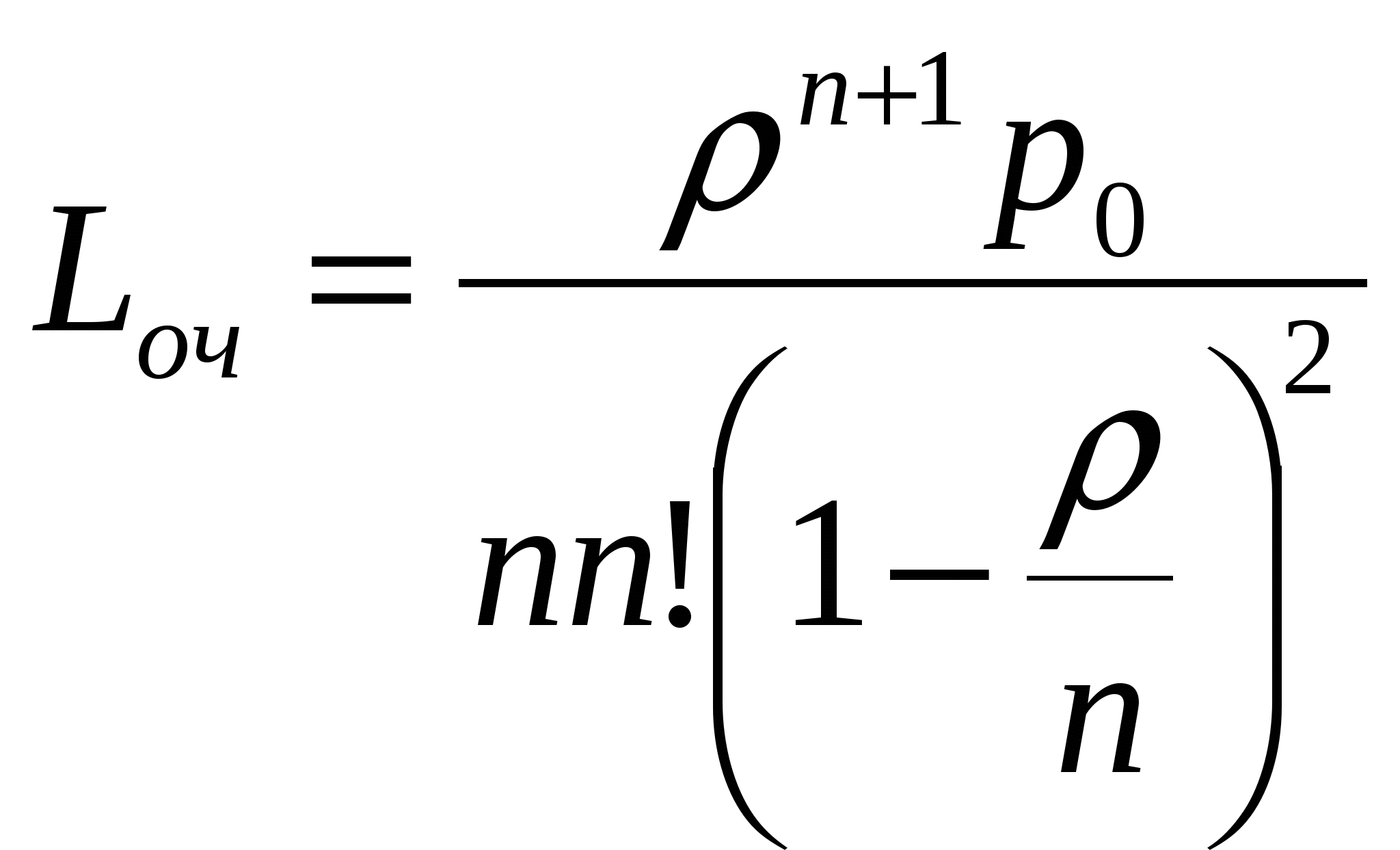

(76)

Тогда среднее число заявок в системе: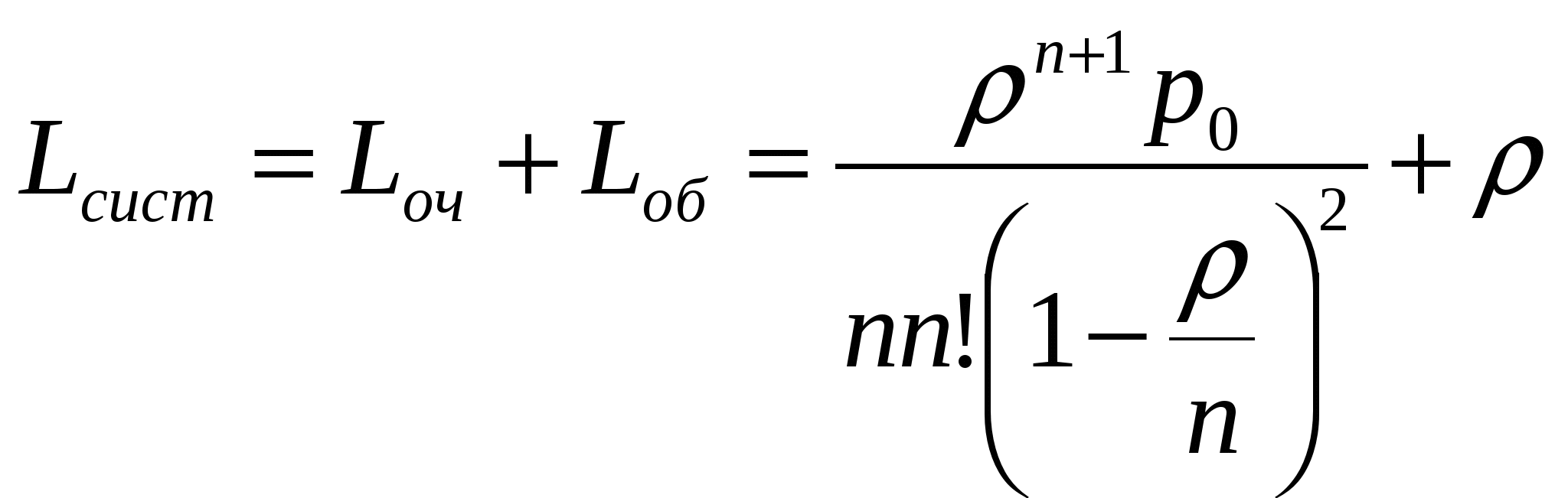

(77)

Среднее время пребывания заявки в системе (в очереди):

(78)

(79)
Многоканальную СМО с неограниченной очередью можно рассмотреть в системе Mathcad.