методичка имитационное моделирование. 1 Основные понятия теории массового обслуживания
 Скачать 0.52 Mb. Скачать 0.52 Mb.
|
|
Содержание Введение……………………………………………………………………………………………..3 1 Основные понятия теории массового обслуживания……………………………....4 2 Одноканальная СМО с отказами…………………………………………………….6 3 Многоканальная СМО с отказами………………………………………………….10 4 Одноканальная СМО с ожиданием…………………………………………..…..15 5 Одноканальная СМО с ограниченной очередью……………………………..……19 6 Многоканальная СМО с неограниченной очередью………………………….…..22 7 Многоканальная СМО с ограниченной очередью…………………………….…..28 Многоканальная с ожиданием Заключение………………………………………………………………………………………....33 Задачи для самостоятельного решения Введение Сложный характер рыночной экономики и современный уровень предъявляемых к ней требований стимулируют использование более серьезных методов анализа ее теоретических и практических проблем. В последние десятилетия значительный вес в экономических исследованиях приобрели математические методы. Математическое моделирование все более и более становится одним из основных и наиболее плодотворных методов изучения экономических процессов и объектов. Математический анализ экономических задач органично превращается в часть экономики. Положительная оценка этого подтверждается и тем, что начиная с 1969 г. Нобелевские премии в области экономики присуждаются, как правило, за экономико-математические исследования. Одним из важных разделов экономико-математического моделирования является теория массового обслуживания, представляющая собой теоретические основы комплекса вопросов эффективности конструирования и эксплуатации систем массового обслуживания. Системы массового обслуживания встречаются во многих областях экономики (производство, техника, военная область, быт и др.) и предназначены для многократного использования при выполнении однотипных задач. Основоположником теории массового обслуживания считается известный датский ученый А.К. Эрланг. Являясь сотрудником Копенгагенской телефонной компании, он опубликовал в 1909 г. работу "Теория вероятностей и телефонные переговоры", в которой решил ряд задач по теории систем массового обслуживания с отказами. Значительный вклад в создание и разработку общей теории массового обслуживания внес выдающийся советский математик А.Я. Хинчин. Его первые труды в этой области стали появляться с 1930 г., когда ему, как члену Совета депутатов, была поручена работа в отделе связи. Благодаря результатам А.Я. Хинчина значительно сократилось время проводившейся тогда автоматизации московской городской телефонной сети, существенно снизились стоимости работ и было введено много технических усовершенствований. Последующие работы А.Я. Хинчина в этой области были изданы после его смерти, в 1963 г., в виде монографии. Сам термин теория массового обслуживания предложен А.Я. Хинчиным. В зарубежной литературе чаще используется название теория очередей. Предлагаемое учебное пособие посвящено изложению основ теории массового обслуживания и ее применению в моделировании систем массового обслуживания различных областей экономики. При этом рассматриваются простейшие системы, в которых протекает марковский случайный процесс "гибели и размножения". 1 Основные понятия теории массового обслуживания Системой массового обслуживания (СМО)называется комплекс взаимосвязанных элементов, состоящий из некоторого числа обслуживающих единиц (каналов), в котором происходит удовлетворение массовых запросов (требований), поступающих в систему в случайные моменты времени. Обслуживание каждой заявки длится в течение некоторого случайного времени и зависит от показателей эффективности системы. После того, как заявка обслужена, она покидает канал, и система готова к приему очередной заявки. Примеры СМО - телефонная станция, автостоянка, кассир магазина, служба занятости. Основные элементы СМО - источник требований, входящий поток заявок, каналы обслуживания, выходящий поток заявок. Предметом теории СМО является построение математических моделей (т. е. образов реального экономического объекта, описанных с помощью уравнений, формул, графиков, схем и т. д.) для теоретического анализа и практического использования свойств СМО. Показатели эффективности СМО - характеристики работы системы, описывающие ее способность справляться с потоком заявок. Эффективность функционирования СМО описывается такими показателями: 1) Эффективность использования СМО - абсолютная или относительная пропускные способности системы, среднее число занятых каналов (коэффициент использования СМО), средняя продолжительность использования СМО, интенсивность нагрузки канала; 2) Качество обслуживания заявок - среднее число заявок, обслуженных СМО в единицу времени, вероятность простоя системы, вероятность отказа в обслуживании, среднёе число заявок в очереди, среднее число заявок в системе и др. Входящий Каналы Выходящий  поток Очередь обслуживания поток поток Очередь обслуживания поток  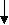 …..… …..… …..… …..…    Поток необслуженных заявок, покидающих систему Рисунок 1: Схема СМО. Поток заявок, поступающих в систему, характеризуется интенсивностью λ, то есть частотой появления заявок в системе, или средним числом заявок, поступающих в систему в единицу времени. Интенсивность μ потока обслуживаний,- это величина, обратная среднему времени обслуживания, или число заявок, обслуженных системой в единицу времени. Интенсивность нагрузки канала обслуживания ρ, - это величина, показывающая среднее число заявок, поступающее в систему за среднее время обслуживания одной заявки: При этом его экономический смысл заключается в том, что показатель ρ, - это среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступающие в систему требования. Условие где п - число каналов обслуживания, означает, что необходимое число каналов обслуживания должно быть больше ρ. Классификация СМО: По дисциплине обслуживания: — СМО с отказами, когда заявка, поступившая в систему в момент, когда все каналы заняты, остается необслуженной; — СМО с ожиданием (очередью), в которых заявка в случае занятости всех каналов становится в очередь и ожидает обслуживания; — Системы с ограничением длины очереди; — Системы с ограниченным временем ожидания; По месту нахождения источника требований: — Замкнутые СМО, когда источник требований находится в самой системе; — Открытые СМО, когда источник требований находится вне системы; По числу обслуживающих каналов: — Одноканальные; — Многоканальные. 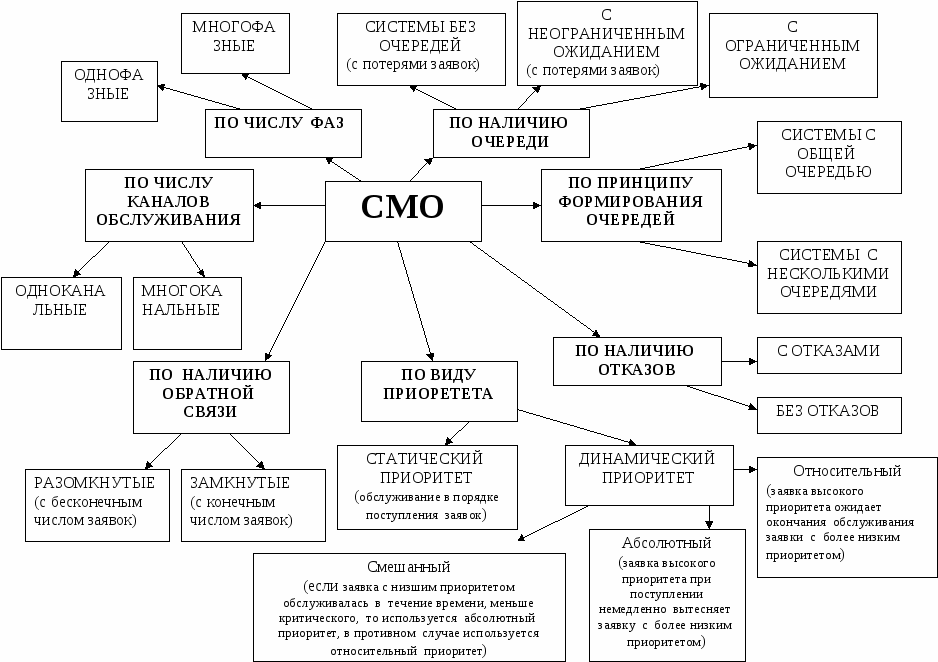 2 Одноканальная СМО с отказами Рассмотрим упорядоченное множество состояний некоторой системы S : S0,S1,S2,…,Sk,…; предположим, что все потоки, переводящие систему из состояния в состояние, - простейшие. Пусть для любого состоянияSk переходы возможны только в соседние состояния: либо в Sk-1,либо в Sk +].Граф состояний такой системы изображен на рисунке номер 2: λ01 λ12 λ23 λk-1,k λk,k+1 λn-1,n 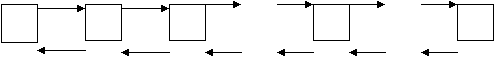 .….. …… .….. …… S0 S1 S2 Sk Sn …… …… λ10 λ21 λ-32 λk,k-1 λk+1,k λn,n-1 Рисунок 2: Граф состояний одноканальной СМО с отказами. Случайные процессы, происходящие в таких системах, имеют специальное название, традиционно происходящее из биологии: схема гибели и размножения (состояние Sk соответствует некоторой популяции численностью k, смена состояния происходит при рождении либо гибели одного члена популяции). Рассмотрим систему с одним каналом обслуживания, в которую поступает простейший поток заявок с интенсивностью λ. Если в момент поступления очередной заявки канал занят, то заявка покидает систему необслуженной. Такие системы называются системами без ожидания, или с отказами в обслуживании. Пусть поток обслуживаний имеет интенсивность μ. Граф состояний такой системы показан на рисунке номер 3:   λ λ  S0 S1 S0 S1μ Рисунок 3: Система без ожидания. Система имеет два состояния: S0 – канал свободен и готов к приему очередной заявки; S1 – канал занят. Эти величины можно интерпретировать как вероятности того, что заявка будет обслужена либо получит отказ: 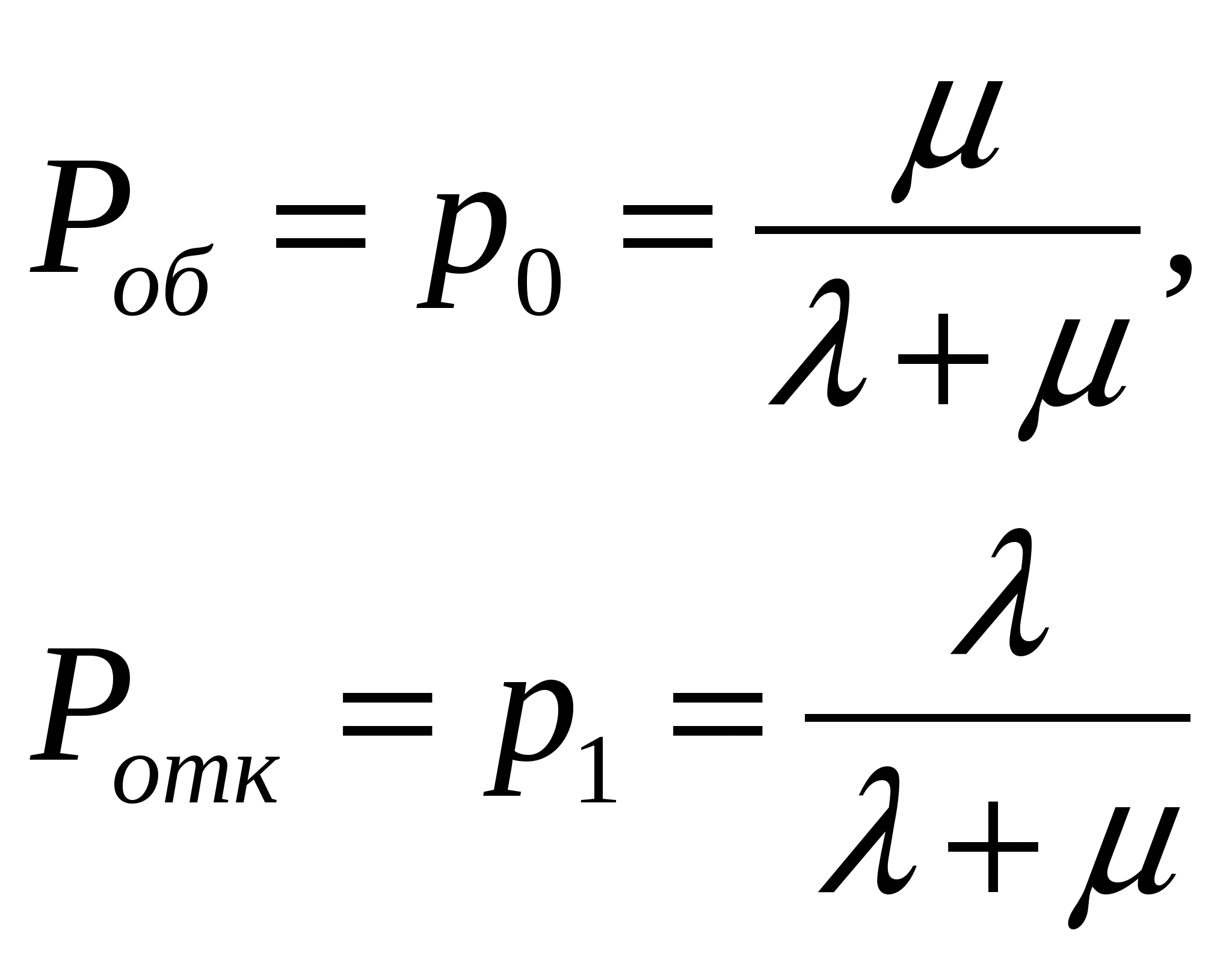 Относительная пропускная способность системы, то есть доля всех обслуженных заявок из числа всех поступивших в систему, равна вероятности обслуживания: Абсолютная пропускная способность системы, то есть число обслуженных заявок в единицу времени, - это произведение интенсивности потока заявок на долю всех обслуженных заявок: Интенсивность μ потока обслуживаний П0б есть производительность канала. Имеет место равенство где Тоб - среднее время обслуживания одной заявки, относящееся только к обслуженным заявкам, т.е. математическое ожидание М [Т0б] случайной величины Т0б. Стационарность потока означает, что его вероятностные характеристики не зависят от времени. Предельные характеристики эффективности функционирования одноканальной СМО с отказами(таблица) Пример. Пусть одноканальная СМО с отказами представляет собой один пост ежедневного обслуживания (ЕО) для мойки автомобилей. Заявка - автомобиль, прибывший в момент, когда пост занят, - получает отказ в обслуживании. Интенсивность потока автомобилей Требуется определить в установившемся режиме предельные значения: относительной пропускной способности q; абсолютной пропускной способности А; вероятности отказа Pотк ; Сравните фактическую пропускную способность СМО с номинальной, которая была бы, если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали один за другим без перерыва. Решение 1. Определим интенсивность потока обслуживания: 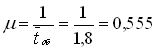 . .2. Вычислим относительную пропускную способность: 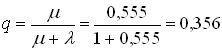 . .Величина q означает, что в установившемся режиме система будет обслуживать примерно 35% прибывающих на пост ЕО автомобилей. 3. Абсолютную пропускную способность определим по формуле: Это означает, что система (пост ЕО) способна осуществить в среднем 0,356 обслуживания автомобилей в час. 4. Вероятность отказа: Это означает, что около 65% прибывших автомобилей на пост ЕО получат отказ в обслуживании. 5. Определим номинальную пропускную способность системы: 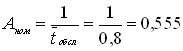 (автомобилей в час). (автомобилей в час). Оказывается, что Аном в 1,5 раза 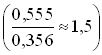 больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания. больше, чем фактическая пропускная способность, вычисленная с учетом случайного характера потока заявок и времени обслуживания. Решение задачи можно осуществить в Mathcad. Пример: Обслуживаются автомобили на посту мойки для автомобилей. Автомобиль, прибывший в момент , когда пост занят, получает отказ. Интенсивность потока автомобилей λ=1 ( автомобиль в час). Средняя продолжительность обслужив. Тобс=1,8 часа. Найти в установившемся режиме: относит. пропускную способность Q; абсолютную пропускную способность А; вероятность отказа Ротк. сравнить фактическую способность с номинальной, которая была бы , если бы каждый автомобиль обслуживался точно 1,8 часа и автомобили следовали бы один за другим без перерыва. Фрагмент решения задачи в Mathcad.  3 Многоканальная СМО с отказами Задача исследования таких СМО впервые возникла в области телефонии и была решена в 1909 г. А.К. Эрлангом. Состояния системы занумеруем по числу занятых каналов. Для СМО с отказами это означает, что мы нумеруем состояния по числу заявок, находящихся в системе, т.е. под обслуживанием, поскольку каждый канал в любой момент времени либо свободен, либо обслуживает только одну заявку. Таким образом, СМО может находиться только в одном из ледующих п + 1 состояний: λ01=λ λ12= λ λk-1,k= λ λk,k+1= λ λn-2,n-1= λ λn-1,k= λ            ……. .….. ……. .….. S0 S1 Sk Sn-1 Sn       ……. ……. ……. …….λ10=μ λ21=2μ λk,k-1=kμ λk+1,k = λn-1,n-2= λn,n-1=nμ =(k+1)μ =(n-1) μ Рисунок номер 4: функционирование системы S. Если СМО находится в состоянии Sk (k=0,1,…,n-1), т. е. когда k каналов заняты обслуживанием заявок, а остальные n-k каналов свободны, то перескок ее в состояние Sk+1 происходит при поступлении на вход новой заявки. Таким образом, по стрелкам слева направо из любого состояния в соседнее состояние справа систему переводит один и тот же входящий поток заявок Пвх с интенсивностью λ. Следовательно, плотность вероятности перехода λk,k+1 (k = 0, 1, ..., n-1) из любого k-го состояния в (k+1)-е состояние равна λ: λ01 = λ12 =…= λn-1,n = λ (15) что и проставлено над стрелками, слева направо. Т.к. входящий поток Пвх простейший, то он является ординарным, т.е. заявки поступают по одной. Поэтому СМО, меняя свои состояния слева направо, не может перескочить через состояние, а переходит только в соседнее справа состояние. По этой причине на графе (рисунок 4) отсутствуют стрелки, перескакивающие через состояния слева направо. Вероятность того, что одновременно, точно в один и тот же момент, освободятся более одного канала, пренебрежимо мала, т.е. такие события практически невозможны. Поэтому на графе нет стрелок, "перескакивающих" через состояния справа налево. На переход занятого канала в состояние свободного действует простейший поток обслуживания Поб с интенсивностью μ. Но тогда переход СМО в целом из состояния Sk (в котором k каналов заняты, а n-k свободны) в состояние Sk-1 (в котором по сравнению с предыдущим освободился один из kзанятых каналов) происходит под воздействием суммарного потока обслуживаний Пkоб, представляющего собой результат наложения k потоков обслуживаний Поб, действующих на каждый из kзанятых каналов. При этом интенсивность суммарного потока равна сумме интенсивностей слагаемых потоков. р0,: или, с учетом формулы получим формулы Эрланга: где ρ - показатель нагрузки канала обслуживания. Формулы для вероятностей предельных состояний буду иметь вид: Приведем формулы для расчета основных показателей эффективности работы системы. Число каналов, которые необходимо иметь, чтобы система справлялась с потоком заявок, определим из условия В этом случае выполняется соотношение которое означает, что число заявок, поступивших в систему за единицу времени, не превосходит числа заявок, обслуженных системой за это же время. Вероятность отказа в обслуживании заявки определим как вероятность того, что при поступлении заявки в систему все п ее каналов будут заняты: Отсюда вероятность обслуживания (а также и относительная пропускная способность системы) равны вероятности противоположного события: Абсолютная пропускная способность - число заявок, обслуженных системой в единицу времени: Так как каждый канал обслуживает μ заявок в единицу времени, то среднее число занятых каналов можно вычислить: или Формула Литтла показывает, что среднее время Тсис пребывания заявки в СМО равно среднему числу заявок в системе Nсис, деленному на интенсивность λ входящего потока заявок, или, другими словами, среднее время Тсис пребывания заявки в СМО прямо пропорционально среднему числу заявок в системе Т сис с коэффициентом прямой пропорциональности, равным обратной величине интенсивности λ входящего потока заявок. Среднее время обслуживания каналом одной заявки: Поток обслуживания Поб каждым каналом будет простейшим с интенсивностью Где Многоканальную СМО с отказами можно решить в Mathcad. |
