Ксения№3. Вариант Одноканальная смо с отказами
 Скачать 84.27 Kb. Скачать 84.27 Kb.
|
|
Вариант 9. Одноканальная СМО с отказами Интенсивность потока обслуживания: Интенсивность нагрузки: ρ = λ*tобс = 140*1/60 = 2.333 Вероятность, что канал свободен: Следовательно, 30% в течение часа канал будет не занят, время простоя равно tпр = 18 мин. Доля заявок, получивших отказ: pотк = 1 - p0 = 1 - 0.3 = 0.7 Относительная пропускная способность: Q = p0 = 0.3 Абсолютная пропускная способность: A = Q*λ = 0.3*140 = 42 заявок/час. Среднее время простоя СМО: tпр = pотк*tобс = 0.7*0.0167 = 0.0117 час Среднее число обслуживаемых заявок: Lобс = ρ*Q = 2.333*0.3 = 0.7 Многоканальная СМО с отказами (3 телефона). Вероятность, что канал свободен: 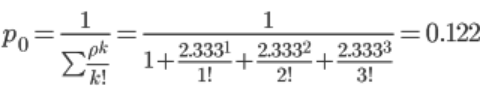 занят 1 канал: заняты 2 канала: заняты 3 канала: Вероятность отказа (вероятность того, что канал занят): Относительная пропускная способность: Q = pобс. pобс = 1 - pотк = 1 - 0.259 = 0.741 Среднее число каналов, занятых обслуживанием: nз = ρ*pобс = 2.333*0.741 = 1.729 Абсолютная пропускная способность: A = pобс*λ = 0.741*140 = 103.731 заявок/час. Среднее время простоя СМО: tпр = pотк*tобс = 0.259*0.0167 = 0.00432 Среднее число обслуживаемых заявок: Lобс = ρ*Q = 2.333*0.741 = 1.729 ед. Среднее время пребывания заявки в СМО: Одноканальная СМО с неограниченной очередью. Интенсивность потока обслуживания: Интенсивность нагрузки: ρ = λ*tобс = 6*3/60 = 0.3 Поскольку ρ < 1, то очередь не будет расти бесконечно, следовательно, предельные вероятности существуют. Вероятность, что канал свободен: p0 = 1 - ρ = 1 - 0.3 = 0.7 p1 = ρk(1 - ρ) = 0.31(1 - 0.3) = 0.21 Относительная пропускная способность: Q = pобс = 1. Абсолютная пропускная способность: A = λ = 6 заявок/час. Среднее число заявок в очереди: Среднее время ожидания заявки в очереди: Среднее число заявок в системе. LCMO = Lоч + Lобс = 0.129 + 0.3 = 0.429 ед. Среднее время пребывания заявки в СМО: |
