Теория Вероятности и Мат статистика ВСЕ темы с описанием Малова. Твимс. 1. Основные понятия теории вероятностей. Пространство элементарных событий. Алгебра событий, основные законы событий. 2

• Название: 1. Основные понятия теории вероятностей. Пространство элементарных событий. Алгебра событий, основные законы событий. 2
• Анкор: Теория Вероятности и Мат статистика ВСЕ темы с описанием Малова
• Дата: 07.10.2022
• Размер: 3.92 Mb.
• Имя файла: Твимс.docx
• Тип: Закон; #720524

Оглавление

1.Основные понятия теории вероятностей. Пространство элементарных событий. Алгебра событий, основные законы событий. 2

2.Основные аксиомы теории вероятностей. 3

3.Классическое определение вероятностей. Геометрический метод задания вероятностей. 3

4.Условная вероятность. Независимость событий. 4

5.Формула полной вероятности. Формула Байеса. 5

6.Последовательность независимых испытаний. Формула Бернулли. 7

7.Теорема Пуассона 7

8.Случайная величина. Законы распределения дискретных случайных величин. 8

9.Функция распределения случайной величины и ее свойства. 11

10.Плотность распределения и ее свойства. 11

11.Распределение двумерной случайной величины и ее свойства. 12

12.Плотность распределения двумерной случайной величины и ее свойства. 14

13.Условные законы распределения двумерной случайной величины. 15

14.Зависимые и независимые случайные величины. 16

15.Общее определение математического ожидания (МО) и его свойства. 17

16.Дисперсия и ее свойства. 18

17.Моменты распределения одномерной случайной величины. 19

18. Ковариация, коэффициент корреляции. 20

19.Характеристические функции и их свойства 22

20.Центральная предельная теорема (знать что такое сходимость по вероятности, слабая сходимость) 24

21.Основные законы распределения вероятностей случайной величины. Биномиальный, Пуассоновский законы. Геометрическое распределение. 25

22.Равномерное, экспоненциальное распределение случайной величины. 26

23.Нормальное распределение. Функция Лапласа. 27

1. 
   Основные понятия теории вероятностей. Пространство элементарных событий. Алгебра событий, основные законы событий.
   

Два события называются совместными в данном опыте, если появление одного из них не исключает появления другого в этом опыте. Например, при подбрасывании двух симметричных монет произошли события A – выпал «герб» и В – выпала «цифра», они являются совместными.

Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании. Например, несовместными являются попадание и промах при одном выстреле.

Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными.

Два события называются противоположными, если появление одного из них равносильно непоявлению другого. Например, события: выпал «герб» и выпала «цифра» - при одном подбрасывании симметричной монеты являются противоположными

Полная группа событий – множество событий 1 2 , ,..., , A A An если они попарно несовместны, появление одного и только одного из них является достоверным событием. Поясним понятие полной группы на примере:

Рассмотрим события, появляющиеся при подбрасывании игрального кубика (т.е. кубика, на гранях которого записаны цифры 1,2,3,4,5,6 или изображены знаки, соответствующие этим цифрам). Когда кубик упадет, то верхней гранью окажется грань с одной из этих цифр. Событие: «верхней гранью оказалась грань с цифрой k » обозначим через ( 1,6). A k k  События A1 A2 A3 A4 A5 A6 образуют полную группу.

Элементарные исходы (элементарные события или шансы) – события, которые могут наступить в результате опыта и которые невозможно (или нет необходимости) разложить на более простые составляющие события. Например, события A1 A2 A3 A4 A5 A6 - элементарные исходы при подбрасывании кубика.

Пространство элементарных событий — множество {\displaystyle \Omega }  всех различных исходов случайного эксперимента. Элемент этого множества {\displaystyle \omega \in \Omega } называется элементарным событием или исходом. 

Простейшие неразложимые результаты опыта называются элементарными событиями (ωi), а вся совокупность элементарных событий называется пространством элементарных событий Ω={ωi}. С каждым опытом связано свое пространство элементарных событий Ω. Например, игральная кость подбрасывается один раз. Элементарные события: w1 – появление 1, w2 – 2, w3 – 3, w4 – 4, w5 – 5, w6 – 6. Пространство элементарных событий W={w1, w2, w3, w4, w5, w6}.

2. 
   Основные аксиомы теории вероятностей.
   

Аксиома 1. Каждому событию соответствует определенное число, удовлетворяющее условию и называемое его вероятностью.

Аксиома 2. Вероятность достоверного события равна единице.

Аксиома 3. Вероятность невозможного события равна нулю.

Аксиома 4. (аксиома сложения). Вероятность суммы двух несовместных событий равна сумме их вероятностей.

3. 
   Классическое определение вероятностей. Геометрический метод задания вероятностей.
   

Вероятностью события называется отношение числа благоприятствующих этому событию исходов к общему числу всех равновозможных несовместных элементарных исходов, образующих полную группу. Вероятность события A обозначается через P (A). По определению

P(A)=n/m

Где m – число элементарных исходов, благоприятствующих событию A;

n – число всех равновозможных элементарных исходов опыта

Эксперимент удовлетворяет классическому определению вероятности, если пространство элементарных исходов состоит из конечного |Ω| = N числа равновозможных исходов. В этом случае вероятность любого события А вычисляется по формуле: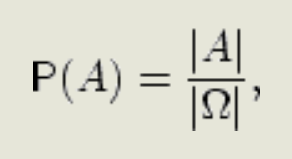



называемой классическим определением вероятности.

Также эту формулу читают как: «вероятность события A равна отношению числа исходов, благоприятствующих событию A, к общему числу исходов»

Подход, называемый геометрическим определением вероятности:

Вероятность наступления некоторого события A в испытании равна отношению , где G – геометрическая мера, выражающая общее число всех возможных и равновозможных исходов данного испытания, а g – мера, выражающая количество благоприятствующих событию A исходов. На практике в качестве такой геометрической меры чаще всего выступает длина или площадь, реже – объём.

4. 
   Условная вероятность. Независимость событий.
   

Условная вероятность:





Свойства:





Также иными словами:




События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.

5. 
   Формула полной вероятности. Формула Байеса.
   

Собственно, продолжаем. Рассмотрим зависимое событие  , которое может произойти лишь в результате осуществления одной из несовместных гипотез  , которые образуют полную группу. Пусть известны их вероятности   и соответствующие условные вероятности  . Тогда вероятность наступления события   равна:



Эта формула получила название формулы полной вероятности. 

Материал тесно связан с содержанием предыдущего параграфа. Пусть событие   наступило в результате осуществления одной из гипотез  .  Как определить вероятность того, что имела место та или иная гипотеза?

При условии, что событие   уже произошло, вероятности гипотез переоцениваются по формулам, которые получили фамилию английского священника Томаса Байеса:

 – вероятность того, что имела место гипотеза  ;
 – вероятность того, что имела место гипотеза  ;
 – вероятность того, что имела место гипотеза  ;
…
 – вероятность того, что имела место гипотеза  .

На первый взгляд кажется полной нелепицей – зачем пересчитывать вероятности гипотез, если они и так известны? Но на самом деле разница есть:

 – это априорные (оцененные до испытания) вероятности.

 – это апостериорные (оцененные после испытания) вероятности тех же гипотез, пересчитанные в связи «со вновь открывшимися обстоятельствами » – с учётом того факта, что событие   достоверно произошло.

6. 
   Последовательность независимых испытаний. Формула Бернулли.
   

Независимые испытания:
Пусть производится несколько испытаний. Если вероятность появления некоего события А в каждом из них не зависит от исходов остальных испытаний, то оно является независимым. При этом под словосочетанием «независимые испытания» часто подразумевают повторные независимые испытания – когда они осуществляются друг за другом.

Последовательностью независимых испытаний называется конечная вероятностная схема, в которой вероятности элементарных событий определяется формулой  =  , как произведение вероятностей исходов отдельных испытаний. Ее называют еще схемой независимых испытаний или полиномиальной схемой.

Формула Бернулли:



Примечание: формула Бернулли справедлива только для тех независимых испытаний, в которых вероятность p события A сохраняется постоянной.

7. 
   Теорема Пуассона
   

Формула Пуассона:



Распределение Пуассона:

8. 
   Случайная величина. Законы распределения дискретных случайных величин.
   

Случайная величина:













Формула дисперсии:



Среднее квадратическое\стандартное отклонение:



Пример дисперсии:

9. 
   Функция распределения случайной величины и ее свойства.
   

Функция распределения случайной величины:



Свойства функции распределения случайной величины:

10. 
    Плотность распределения и ее свойства.
    

Плотность распределения:



Свойства плотности распределения:

11. 
    Распределение двумерной случайной величины и ее свойства.
    

12. 
    Плотность распределения двумерной случайной величины и ее свойства.
    

13. 
    Условные законы распределения двумерной случайной величины.
    

14. 
    Зависимые и независимые случайные величины.
    

15. 
    Общее определение математического ожидания (МО) и его свойства.
    

Формула дисперсии:



Среднее квадратическое\стандартное отклонение:

16. 
    Дисперсия и ее свойства.
    

Пример дисперсии:

17. 
    Моменты распределения одномерной случайной величины.
    

18. 
    Ковариация, коэффициент корреляции.
    

19. 
    Характеристические функции и их свойства
    

Определение:



Свойства:

1. Характеристическая функция всегда существует:



Док-во: Воспользуемся свойством 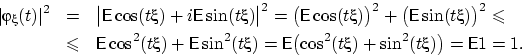, равносильным неравенству :



2. По характеристической функции однозначно восстанавливается распределение (значение случайной величины). Т.е. если две случайные величины имеют одинаковые характеристические функции, то и распределения этих величин совпадают.

Если модуль характеристической функции интегрируем на всей прямой, то у случайной величины есть плотность распределения, и она находится по формуле:



3. Характеристическая функция случайной величины связана с характеристической функцией случайной величины равенством:



4. Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых: если случайные величины и независимы, то, по свойству (Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий: если   и   независимы и их математические ожидания существуют) математических ожиданий:



5. Пусть существует момент порядка 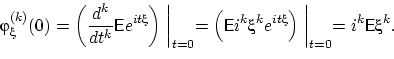  случайной величины  , т.е.  . Тогда характеристическая функция   непрерывно дифференцируема   раз, и её  -я производная в нуле связана с моментом порядка   равенством:



6. Пусть существует момент порядка   случайной величины  , т.е.  . Тогда характеристическая функция   в окрестности точки   разлагается в ряд Тейлора:

20. 
    Центральная предельная теорема (знать что такое сходимость по вероятности, слабая сходимость)
    

Говорят, что последовательность случайных величин   сходится слабо или по распределению к случайной величине   и пишут:  , если для любого   такого, что функция распределения   непрерывна в точке  , имеет место сходимость  при  .

Слабая сходимость — это сходимость функций распределения во всех точках непрерывности предельной функции распределения.

Сходимость по вероятности влечёт слабую сходимость. Обратное утверждение в общем случае смысла не имеет (см. замечание 25). Однако из слабой сходимости к постоянной вытекает сходимость по вероятности.

Свойство: Если  , и функция распределения   непрерывна в точках   и  , то  . Наоборот, если во всех точках   и   непрерывности функции распределения   имеет место сходимость  , то  .

Свойство 20.

1. Если  , то  .

2. Если  , то  .

Итак, сходимость по вероятности влечёт слабую сходимость. Однако из слабой сходимости к постоянной вытекает сходимость по вероятности.

21. 
    Основные законы распределения вероятностей случайной величины. Биномиальный, Пуассоновский законы. Геометрическое распределение.
    

Геометрическое распределение

Говорят, что случайная величина   имеет геометрическое распределение с параметром  , и пишут  , если   принимает значения   с вероятностями  . Случайная величина с таким распределением имеет смысл номера первого успешного испытания в схеме Бернулли с вероятностью успеха  . Таблица распределения   имеет вид:

22. 
    Равномерное, экспоненциальное распределение случайной величины.
    

Равномерное распределение:

Говорят, что   имеет равномерное распределение на отрезке  , и пишут:  , если плотность распределения   постоянна на отрезке   и равна нулю вне него:

 

Очевидно, что площадь под графиком этой функции равна единице и  . Поэтому    является плотностью распределения.

Случайная величина   имеет смысл координаты точки, выбранной наудачу на отрезке  . Вычислим по определению 30 функцию распределения случайной величины  :



Получим следующую непрерывную функцию распределения: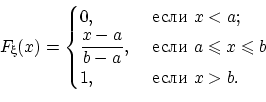

 

Показательное распределение (экспоненциальное):

Говорят, что  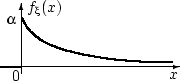 имеет показательное (экспоненциальное) распределение с параметром  , и пишут:  , если   имеет следующую плотность распределения:

    

Функция распределения случайной величины 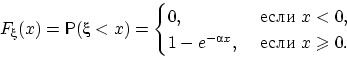  непрерывна:

 

Показательное распределение является единственным абсолютно непрерывным распределением, для которого выполнено свойство «нестарения» (и в этом смысле оно является непрерывным аналогом дискретного геометрического распределения).

23. 
    Нормальное распределение. Функция Лапласа.