Системный анализ. 1. Основные принципы системного анализа Систематический анализ

• Название: 1. Основные принципы системного анализа Систематический анализ
• Анкор: Системный анализ.docx
• Дата: 22.07.2018
• Размер: 50.11 Kb.
• Имя файла: Системный анализ.docx
• Тип: Документы; #21839

1.Основные принципы системного анализа:

1.Систематический анализ:

совокупность методов и средств исследования сложных, многоуровневых и многокомпонентных систем,объектов, процессов, опирающихся на комплексный подход, учет взаимосвязей и взаимодействий междуэлементами системы. С.а. играет важную роль в процессе планирования и управления, при выработке ипринятии управленческих решений.

2. Основоположник кибернетики и теории искусственного интеллекта:

Норберт Винер

3. Различают три ветви науки, изучающей системы:
1) Системологию (теорию систем) которая изучает теоретические аспекты и использует теоретические методы (теория информации, теория вероятностей, теория игр и др.);
2) Системный анализ (методологию, теорию и практику исследования систем), которая исследует методологические, а часто и практические аспекты и использует практические методы (математическая статистика, исследование операций, программирование и др.);
3) Системотехнику, системотехнологику (практику и технологию проектирования и исследования систем). 

4. Математическое программирование – это наука, занимающаяся разработкой и практическим применением методов наиболее эффективного (или оптимального) управления организационными системами (предприятия, фирмы, банки и др.).
5. Определение системы:

Перв. опеделение: система есть средство достижения цели. Причем, системой является не только созд.- объект, но и коллектив создающий его.

Третье опр.: система есть совокупность взаимосвязи элементов, обособленное от среды и взаимодействия с ней как единое целое.

Будем понимать под определением системы (внеш. средой) множество тех элементов системы, которые не являются частями системы, но изменения в любом из которых может повлечь за собой изменение в сост.системы.

6. Модель чёрного ящика:

Модель «черного ящика» - модель системы, представляющая собой структуру с известными выходными и входными параметрами и неизвестным внутренним устройством. Исследуя известные параметры, с помощью такой модели можно получить представление о внутреннем устройстве.

Z

↓↓↓

X 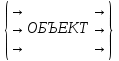Y

↑↑↑



Множество параметров Y называется выходом системы или откликом.
К первой группе входных параметров, которых можно измерить и целенаправленно изменить поддерж. заданный техн.режим.

Вторая группа – контролируемые, но не упр. Входные параметры.

Третья группа – не контр. И не упр. Вход

7. Состояние системы:

Система есть совокупность взаимосвязанных элементов обособленное от среды и взаимодействующее с ней как единое целое.

8.Окружение системы:

Будем понимать под окружением системы (внешней средой) множество тех. Элементов системы, которые не являются частями системы, но изменения в любом из которых может повлечь за собой изменение в состоянии системы.

9. Подсистема, элемент, связь, структура, функц. Произв. Системы, процесс:

Подсистемой будем называть выделенное из системы подмножество взаимосвязь. элементов объед. некоторыми целевым назначением.

Элемент неразложимый далее( в данной системе при данном способе рассм и анализа) компонент сложных объектов явлений, процессов.

Связь- перенос материальных, энергетических или информ. Компонентов из одного объекта в др.

Структура – относительно уст. Функция связей между элементами систем

Разл. Структуры:

1) Линейного типа

2) Иерархического типа

3) Сетевого типа

4) Матричного типа

Процесс- количественное или качественное применение характеристик объекта в течении определения времени.

10. Свойства системы:

1) Целостность

2) Разнообразие

3) Эмерджентность

4) Связанность

5) Целенаправленность

6) Устойчивость

7) Жизненного цикла системы

11. Задачи изучения систем:

Три основные задачи:

1. Анализ систем состоит в изучении свойств и поведения систем в разл. Услов.функций. В процессе анализа уст. Численное значение показателей эффективности систем.

2. Синтез систем состоит в построении возможных вариантов систем разл. структурный и параметр. синтез.

3. Оценка и принятие решений закл. в выборе наилучшего варианта системы из нескольких альтернативных и оценка эффективности ф-я системы.

2. Методы и модели системного анализа:

12. Модель объекта

В зрения системном анализе моделью объекта называется материальная и идеальная система, создаваемая и используемая при решений конкретной задачи с целью получения новых знаний об объекте оригинале адекватная ему с точкой изучаемых свойств и более простая, чем оригинал.
13. Требования к модели

Важнейшие требования к любой модели является:
1)адекватность изучаемому объекту в рамке конкретной задачи.
2)реализуемость имеющимся средствам

3. Задача линейного программирования:

14. Задача линейного программирования:

Общей задачей линейного программирования называется задача, которая состоит в определении максимального( минимального) значения целевой функции

F= 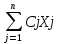(8)

При условиях

(9)

(10)



где  a_ij, b_i, c_j- заданные постоянные величины и  k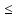m.

Стандартной (или симметричной} задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (9) и (11), где k = m и l = n.

Канонической (или основной) задачей линейного программирования называется задача, которая состоит в определении максимального значения функции (8) при выполнении условий (10) и (11), где k = 0 и l = п.

15. Цель построения, целевая функция и ограничения:

1.Целевая функция – функция, значение которой должно достигнуть искомого (конкретного или экстремального) значения. В excel эта функция записывается в виде формулы, расположенной в определенной ячейке таблицы, поэтому говорят о «целевой ячейке».

2.В большинстве задач целью решения является нахождение экстремального значения некоторой целевой функции( например, нахождение параметров, обеспечивающих получение максимальной прибыли или минимальных затрат).

3.При поиске решения целенаправленному изменению подвергаются, как правило, не один, а несколько параметров (ячеек). Кроме того, на диапазоны изменения параметров могут быть наложены ряды ограничений, которые выражаются в виде формул, описывающих отношения (системы управлений) между значениями параметров и некоторыми величинами.

16. Постановка задачи и производстве товаров и услуг:

Этот класс задач обычно ориентирован на решение вопроса как рациональнее организовать производительный процесс. Целью оптимизации является определение оптимального соотношения объемов между видами выпускаемой продукции, при котором объём реализации достигает максимума. Для этих задач целевая ячейка обычно опр. Объёмом реализации некоторой разнородной продукции в стоимостном выражении.

17. Постановка транспортной задачи:
Под названием “транспортная задача” объединяется широкий круг задач с единой математической моделью. Данные задачи относятся к задачам линейного программирования и могут быть решены симплексным методом. Однако матрица системы ограничений транспортной задачи настолько своеобразна, что для ее решения разработаны специальные методы. Эти методы, как и симплексный метод, позволяют найти начальное опорное решение, а затем, улучшая его, получить оптимальное решение. В общей постановке транспортная задача состоит в отыскании оптимального плана перевозок некоторого однородного груза с баз  потребителям . Различают два типа транспортных задач: но критерию стоимости (план перевозок оптимален, если достигнут минимум затрат на его реализацию) и по критерию времени (план оптимален, если на его реализацию затрачивается минимум времени).
18. Составление скользящих графиков:

Такие графики обычно связаны с расписаниями многосменной работы предприятия в условиях нестационарного спроса на товары или услуги, связанные с деятельностью этого предприятия.
Эти задачи характеризуются наличием многих ограничений действующих в разные периоды времени. Например, спрос на общественный транспорт сильно меняется в зависимости от времени суток, спрос на продаваемые товары в магазине меняется в зависимости от дня недели и времени суток и т. д. Задача состоит в том, чтобы организовать расписание обслуживания клиентов (пассажиров, покупателей и т. п.) таким образом, чтобы издержки от неравномерности спроса были бы минимальны. 

19. Постановка задачи логического выбора:

4. Имитационное моделирование:

20. Определение имитационного моделирования:

По Шеннону «имитационное моделирование» есть процесс конструирования на ЭВМ модели сложной реальной системы, функционирующей во времени и постановки экспериментов на этой модели с целью понять цель системы либо оценить различные стратегии управления, обеспечивающие функционирование данной системы.

21. Этапы имитационного моделирования:

Выделим два этапа:

1) конструирование модели

2) проведение эксперимента

Каждый из этапов использует собственные методы. На первом этапе инф. Обследование и разработка математической модели.
На втором этапе использует метод планирования эксперимента с учетом особенности машинной имитации.

22. Цель имитационного моделирования:

Цели имитационного эксперимента:

Либо понять поведение исследования системы, либо оценить возможные стратегии управления.

23. Случаи использования имитационного модели:

1. Если идет процесса познания объекта моделирования.

2. Если необходимо осуществить наблюдения за поведением компьютерной системы в течение определенного времени.

3. Протекание процессов в системе путем замедление или ускорение явлений.

4. Если модель используют для предсказания так называемых узких мест.

5. Если имитационного моделирование оказывается единственным способом исследования.

24. Достоинства и недостатки имитационного моделирования:

Достоинства:

1.Модель позволяет описать моделируемый процесс.

2. Модель обладает гибкостью варьирования структуры параметров и алгоритмов.

3. Применение ЭВМ сокращает время.

Недостатки:

1.Решение, полученное на имитационной модели всегда носит частный характер, так как оно соответствует фиксированным элементам структуры алгоритмам поведения.
2. Большие трудозатраты на создание модели и проведение эксперимента.

25. Составляющие имитационной модели:

1)Компоненты.

2) Переменных.

3) Параметров.

4)Функ. зависимость.

5) Ограничений.

6)Целевых Функций.

Под компонентами понимают сост. части, которые при соот. объед. обр. систему.

Параметры величины, которые исследуют, может выбирать произвольно, то есть управлять ими.

В отличие от них переменные могут быть только опр.видом данной функции.

26. Три представления времени, которое используют при реализации имитационной модели:

При реализации имитационной модели используются обычно три представления времени:

1.реальное время системы, функционирование которой имитируется;

2.модельное время, по которому организуется синхронизация событий в модели;

3.машинное время имитации, отражающее затраты ресурса времени компьютера.

27.Направление испытания имитационной модели:

Испытание имитационной модели включает работы по четырем направлениям:

1.задание исходной информации;

2.верификацию имитационной модели;

3.проверку адекватности модели;

4.калибровку имитационной модели.

5. Химико-технологический процесс (ХТП) как система. Математическое описание структуры потоков в аппарате.

28. Сущность методов исследования потоков:

Сущность указанных методов заключается в том, что на входе потока в аппарат вводят индикатор, а на выходе измеряют его концентрацию как функцию времени. Полученная выходная кривая называется функцией отклика системы на типовое возмущение по составу потока. В качестве индикаторов обычно используются красители, растворы солей и кислот, изотопы и др. вещества.

29. Характеристики функции РВП:

Функция распределения времени пребывания может быть охарактеризована числовыми характеристиками – моментами. Обычно используют размерные моменты нулевого M_o, первого M₁ и второго M₂ порядков. Общая формула для нахождения размерных моментов:

M_s=,

Где S- порядок момента, - дифференциальная функция распределения времени пребывания. Тогда

M₀= M₁= M₂=

30. Типовые модели структуры потоков:

К типовым моделям относится модель идеального перемешивания (МИП) и модель идеального вытеснения (МИВ). Эти модели теоретические и соответствуют идеальным потокам, однако, в ряде случаев их можно использовать для характеристики реальных потоков. К типовым моделям структуры потоков также относятся диффузионная, ячеечная и комбинированные модели. Эти модели характеризуют реальные потоки и при предельных условиях переходят в одну из теоретических моделей – МИВ и МИП.

Модель идеального перемешивания:

Согласно этой модели принимается, что поступающий в аппарат поток мгновенно распределяется по всему объему вследствие полного перемешивания частиц потока. При этом концентрация распределенного вещества во всех точках зоны идеального перемешивания и в потоке на выходе из него одинакова.

Модель идеального вытеснения:

В соответствии с моделью идеального вытеснении принимается поршневое движение потока без перемешивания вдоль потока, при равномерном распределении концентрации вещества в направлении, перпендикулярном движению. При этом время пребывания всех элементов потока в зоне идеального вытеснения одинаково и равно отношению объема зоны вытеснения к объемному расходу жидкости τ = V/v.

Однопараметрическая диффузионная модель:

Модель предполагает, что поток движется в режиме идеального вытеснения, но в нем происходит продольное перемешивание.

Ячеечная модель:
Основывается на том, что движущийся поток рассматривается состоящим из ряда последовательно соединенных ячеек. При этом принимается, что в каждой ячейке поток имеет структуру идеального перемешивания, а между ячейками перемешивание отсутствует.

31. Параметр, от которого зависит количество уравнений в ячеечной модели:

Число ячеек n отражает степень перемешивания в аппарате и, следовательно, его роль в ячеечной модели аналогична критерию Пекле в диффузионной модели. При определении числа ячеек в ряде случаев можно воспользоваться формальной аналогией между числом Пекле Ре и величиной n. Между этими параметрами существует связь, которая выражается зависимостью

n= =

32. Проверка адекватности модели:

По расположению кривых можно судить об адекватности модели. Если кривые расположены достаточно близко друг к другу, то можно сказать, что модель адекватна структуре потока. Иначе модель выбрана неправильно, и все вычисления надо произвести вновь, начиная с этапа выбора модели.

6. Математическое моделирование кинетики химических реакций:

33. Изучения химической кинетики:

Химическая кинетика – раздел химии, который изучает скорость химической реакции и факторы, влияющие на неё.

34. Скорость химической реакции, запись уравнения скорости, знаки «+», «-»:

Количественной характеристикой, которая определяет динамику процесса химического превращения, является скорость реакции. Скорость химической реакции – это изменение числа молей одного из компонентов в единицу времени в единице объема:

W=

Где V– объём, N- число образовавшихся или прореагировавших молей; t - время.

Знак «+» указывает, что концентрация вещества накапливается в результате реакции, знак «-», что убывает.

Запишем стехиометрическое уравнение реакции:

А+В С

35. Прямая задача кинетики:

Прямая задача заключается в получении кинетических кривых по известным механизмам реакций и уравнениям кинетики при заданных значениях констант скоростей реакции.

Необходимо по известному механизму, заданным константам скоростей, начальным значениям концентраций веществ получить кинетические кривые (зависимости концентраций веществ во времени).

36. Обратная задача кинетики, две постановки обратной

задачи:

Обратная задача заключается в определении механизма реакции и неизвестных констант скоростей по известным экспериментальным данным (кинетическим кривым).

Часто перед исследователями возникает задача определения неизвестных параметров математического описания или даже уравнений модели, так называемая обратная задача кинетики. Это означает, что нужно выбрать такие уравнения и конкретные значения их параметров, чтобы результаты моделирования согласовывались с экспериментальными данными. При этом исходными сведениями являются результаты химических опытов.

Постановки решения обратной задачи:

1. Известен механизм реакции и имеются экспериментальные данные по кинетике химических реакций. Численные значения части или всех параметров реакции не известны. Требуется найти такие значения параметров реакции, чтобы полученные кинетические кривые наилучшим образом аппроксимировали экспериментальные данные.

37. Этапы построения математической модели химической реакции:

1. Получение экспериментальных данных

2. Формулирование гипотезы о механизме протекании реакции.
3. Получение математической модели кинетики химической реакции.

4. Формулирование критерия адекватности.

5. Отыскание параметров модели кинетики химических реакций, минимизирующих критерий адекватности.

6. Принятие полученной модели или повторение пунктов 3-6.

38. Метод Эйлера для решения системы диф. уравнений. Запись уравнения Эйлера.

Если задачу об отыскании решений дифференциального уравнения удаётся свести к конечному числу алгебраических операций, операций дифференцирования и интегрирования известных функций, то говорят, что дифференциальное уравнение интегрируется в квадратурах.

В приложениях крайне редко встречаются уравнения. интегрируемые в квадратурах. Для исследования и решения уравнений, которые не интегрируются в квадратурах, используются численные методырешения задачи Коши.

 

Численное решение задачи Коши y' = f(x, y), y(a) = y₀ на отрезке [a, b] состоит в построении таблицы приближённых значений y₀,y₁, ..., y_i, ..., y_N решения y = y(x), y(x_i) ≈ y_i ,

в узлах сетки a = x₀< x₁< ...< x_i< ...< x_N = b. Если x_i = a + ih, h = (b-a)/N, то сетка называется равномерной.

 

Численный метод решения задачи Коши называется одношаговым, если для вычисления решения в точке x₀ + h используется информация о решении только в точке x₀.

Простейший одношаговый метод численного решения задачи Коши — метод Эйлера.  В методе Эйлера величины y_i вычисляются по формуле: y_i+1 = y_{i + h·f(xi, yi):}

y' = f(x, y),  y(a) = y₀ , x ∈ [a, b],

x_i = a + ih, h = (b-a)/N, i = 0,1 , 2, ..., N,  

y(x_i)≈ y_i ,

y_i+1 = y_i + h·f(x_i, y_i).

Для погрешности метода Эйлера на одном шаге справедлива оценка



а для оценки погрешности решения на всём отрезке [a, b] справедливо


Для практической оценки погрешности можно рекомендовать правило Рунге: производятся вычисления с шагом h — вычисляются значения y^(h)_i, затем производятся вычисления с половинным шагом h/2 — вычисляются значения y^(h/2)_i .

 

За оценку погрешности вычислений с шагом h/2 принимают величину



 

Если соединить точки (x_i,y_i) прямолинейными отрезками, получим ломаную Эйлера — ломаную линию, каждое звено которой с началом в точке (x_i,y_i) имеет угловой коэффициент, равный f(x_i,y_i).

39. Кривые (кинетические кривые):

40. Критерии выбора адекватности модели:
Проверка адекватности модели состоит в сравнении дисперсий модельных и экспериментальных результатов и принятии или отклонении проверяемой гипотезы. В случае непринятия гипотезы осуществляется возврат к этапу 3 (получение математической модели кинетики химической реакции) для проработки следующей гипотезы по всем рассмотренным этапам.