обработка выборочных данных, нахождение интервальных оценок параметров распределения. обработка_выборочных_данных. Обработка выборочных данных. Нахождение интервальных оценок параметров распределения. Проверка статистической гипотезы
 Скачать 41.76 Kb. Скачать 41.76 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. УЛЬЯНОВА (ЛЕНИНА) Кафедра алгоритмической математики ОТЧЕТ по практической работе №3 по дисциплине «Статистический анализ» Тема: Обработка выборочных данных. Нахождение интервальных оценок параметров распределения. Проверка статистической гипотезы.
Санкт-Петербург 2021 Цель работы. Получение практических навыков вычисления интервальных статистических оценок параметров распределения выборочных данных и проверки «справедливости» статистических гипотез. Основные теоретические положения. Интервал (θ*1, θ*2), накрывающий с вероятностью γ истинное значение параметра θ называется доверительным интервалом, а вероятность γ — надежность оценки или доверительной вероятностью. Если интерес представляет ситуация, когда важно сравнения только с одним критическим значением, то использует односторонние доверительные интервалы: для заданного уровня доверия (надежности) γ строят двусторонний доверительный интервал, который затем расширяют за счет одной из его границ. Статистической гипотезой называется любое предположение о генеральной совокупности, проверяемое по выборке. Нулевой (основной) гипотезой H0 называется предположение, которое выдвигается изначально, пока наблюдения не заставят признать обратное. Альтернативной (конкурирующей) гипотезой H1 называется гипотеза, которая противоречит нулевой гипотезе H0 и которую принимают, если отвергнута основная гипотеза. Постановка задачи. Для заданной надежности определить (на основании выборочных данных и результатов выполнения практической работы №2) границы доверительных интервалов для математического ожидания и среднеквадратичного отклонения случайной величины. Проверить гипотезу о нормальном распределении исследуемой случайной величины с помощью критерия Пирсона 𝜒2. Дать содержательную интерпретацию полученным результатам. Выполнение работы. Так как у нас неизвестны σг и N, то в таком случае мы можем рассчитать точность оценки по формуле (1) 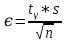 (1) (1)Тогда для заданных уровней доверия, получим доверительные интервалы для математического ожидания, приведенные в табл. 1. Таблица 1 - доверительный интервалы для математического ожидания.
При различной доверительной вероятности величина доверительного интервала будет разной. Чем больше доверительная вероятность, тем больше доверительный интервал. Теперь для вычисления границ доверительного интервала для среднеквадратичного отклонения определим по таблице значение q(γ,n). Для нашей выборки получим q(0.95, 109)=0.138 и q(0.99, 109) =0.19. Рассчитанные доверительные интервалы для среднеквадратичного отклонения занесены в табл. 2. Таблица 2 — доверительные интервалы для среднеквадратичного отклонения.
Для проверки гипотезы была реализована функция, которая находит критическую точку и сравнивает ее с наблюдаемым значением. Результат работы функции приведен на рис. 1. Р  исунок 1 — проверка гипотезы о нормальности заданного распределения. исунок 1 — проверка гипотезы о нормальности заданного распределения.По результатам работы функции принимаем гипотезу о том, что наша величина распределена нормально. Выводы. В ходе практической работы были рассчитаны доверительные интервалы для математического ожидания и среднеквадратичного отклонения при разной доверительной точности, также была принята гипотеза о нормальной распределении нашей величины. ПРИЛОЖЕНИЕ A import csv import random import matplotlib.pyplot as plt import numpy as np import pandas as pd import math import scipy.stats as sts import copy from scipy.stats import chi2 df1 = pd.read_csv("resources/voices_in_my_head.csv", encoding='utf8', index_col=False) class Something: v = 109 k = 1 + math.floor(math.log2(v)) def __init__(self, df, col_idx): self.name = df.columns[col_idx] self.data = df[df.columns[col_idx]].values self.ranged_seq = sorted(self.data) self.h = (self.ranged_seq[-1] - self.ranged_seq[0]) / Something.k self.var_srs = [0] * Something.k self.xi = [0] * (Something.k + 1) self.freq = [0] * Something.k self.rel_freq = [0] * Something.k self.cum_freq = [0] * Something.k self.cum_rel_freq = [0] * Something.k self.xi_plus_half_of_h = [0] * Something.k self.c = 0 self.ui = [0] * Something.k self.vi = [0] * 4 self.mu_i = [0] * 4 self.x_avr_mean = 0 self.x_avr_mean_ln = 0 self.u_avr = 0 self.dispersion = 0 self.sd = 0 self.fixed_dispersion = 0 self.fixed_sd = 0 self.asm_cef = 0 self.kurtosis_cef = 0 self.mode = 0 self.median = 0 self.variation_cef = 0 self.conf_interval_accuracy = {} self.conf_interval_accuracy_sd = {} self.cool_dict = {} def calc_ivs(self): x0 = self.ranged_seq[0] xk = x0 xk1 = xk + self.h for i in range(Something.k): if i == 0: self.var_srs[i] = "[" + str(xk) + "-" + str(xk1) + "]" else: self.var_srs[i] = "(" + str(xk) + "-" + str(xk1) + "]" xk = xk1 xk1 += self.h def calc_new_vs(self): new_vs = [0] * Something.k x0 = self.ranged_seq[0] xk = x0 xk1 = xk + self.h for i in range(Something.k): if i == 0: new_vs[i] = "(-inf" + str(xk) + "-" + str(xk1) + "]" elif i == Something.k - 1: new_vs[i] = "(" + str(xk) + "-" + str(xk1) + "+inf)" else: new_vs[i] = "(" + str(xk) + "-" + str(xk1) + "]" xk = xk1 xk1 += self.h return new_vs def calc_xi_arr(self): xi = self.ranged_seq[0] for i in range(Something.k + 1): self.xi[i] = xi xi += self.h def calc_xi_plus_half_of_h(self): for i in range(Something.k): self.xi_plus_half_of_h[i] = self.xi[i] + self.h / 2 def calc_ui(self): if self.k % 2 == 0: self.c = self.xi_plus_half_of_h[Something.k / 2 - 1] if self.freq[Something.k / 2 - 1] >= self.freq[Something.k / 2] \ else self.xi_plus_half_of_h[Something.k / 2] else: self.c = self.xi_plus_half_of_h[Something.k // 2] for i in range(Something.k): self.ui[i] = (self.xi_plus_half_of_h[i] - self.c) / self.h def calc_cond_vi(self): for i in range(4): for j in range(Something.k): self.vi[i] += math.pow(self.ui[j], i + 1) * self.rel_freq[j] def calc_mu_i(self): for i in range(4): if i == 0: self.mu_i[i] = 0 elif i == 1: self.mu_i[i] = (self.vi[1] - self.vi[0] ** 2) * (self.h ** 2) elif i == 2: self.mu_i[i] = (self.vi[2] - 3 * self.vi[1] * self.vi[0] + 2 * (self.vi[0] ** 3)) * (self.h ** 3) elif i == 3: self.mu_i[i] = (self.vi[3] - 4 * self.vi[2] * self.vi[0] + 6 * self.vi[1] * (self.vi[0] ** 2) - 3 * (self.vi[0] ** 4)) * (self.h ** 4) def calc_x_avr_mean_stand(self): for i in range(Something.k): self.x_avr_mean += self.xi_plus_half_of_h[i] * self.rel_freq[i] def calc_x_avr_mean_log(self): for i in range(Something.k): self.x_avr_mean_ln += math.log(self.xi_plus_half_of_h[i]) * self.rel_freq[i] def calc_dispersion_stand(self): x_sqr = 0 for i in range(Something.k): x_sqr += (self.xi_plus_half_of_h[i] ** 2) * self.rel_freq[i] self.dispersion = x_sqr - (self.x_avr_mean ** 2) def calc_sd(self): self.sd = math.sqrt(self.dispersion) def calc_fixed_dispersion(self): self.fixed_dispersion = (Something.v / (Something.v - 1)) * self.dispersion def calc_fixed_sd(self): self.fixed_sd = math.sqrt(self.fixed_dispersion) def calc_mode(self): ind_max = 0 second_ind_max = -1 elem_max = 0 counter = 0 for i in range(Something.k): if self.rel_freq[i] > elem_max: elem_max = self.rel_freq[i] ind_max = i for i in range(Something.k): if self.rel_freq[i] == max and i != ind_max: counter += 1 second_ind_max = i if counter == 0: if ind_max == 0: self.mode = self.xi[ind_max] + self.h * (self.rel_freq[ind_max] / (2 * self.rel_freq[ind_max]) - self.rel_freq[ind_max + 1]) elif ind_max == Something.k - 1: self.mode = self.xi[ind_max] + self.h * (self.rel_freq[ind_max] - self.rel_freq[ind_max - 1]) /\ (2 * self.rel_freq[ind_max] - self.rel_freq[ind_max - 1]) else: self.mode = self.xi[ind_max] + self.h * (self.rel_freq[ind_max] - self.rel_freq[ind_max - 1]) / \ (2 * self.rel_freq[ind_max] - self.rel_freq[ind_max - 1] - self.rel_freq[ind_max + 1]) elif counter == Something.k: self.mode = None else: self.mode = 'multi_mode' def calc_median(self): key_index = 0 for i in range(1, Something.k): if self.cum_rel_freq[i] >= 0.5 > self.cum_rel_freq[i - 1]: key_index = i if key_index != 0: self.median = self.xi[key_index] + (self.h / self.rel_freq[key_index]) *\ (0.5 - self.cum_rel_freq[key_index - 1]) else: self.median = self.xi[key_index] + (self.h / self.rel_freq[key_index]) * 0.5 def calc_variation_cef(self): self.variation_cef = str(round((self.sd / self.x_avr_mean) * 100, 2)) + '%' def calc_asm_cef(self): self.asm_cef = self.mu_i[2] / (self.dispersion ** (3 / 2)) def calc_kurtosis_cef(self): self.kurtosis_cef = (self.mu_i[3] / (self.dispersion ** 2)) - 3 def calc_x_avr_mean_cond(self): for i in range(Something.k): self.u_avr += self.ui[i] * self.rel_freq[i] return self.h * self.u_avr + self.c def calc_dispersion_cond(self): u_sqr = 0 for i in range(Something.k): u_sqr += (self.ui[i] ** 2) * self.rel_freq[i] return (self.h ** 2) * (u_sqr - (self.u_avr ** 2)) def calc_freq(self): |
