контр. 1). Остроугольный (
 Скачать 2.37 Mb. Скачать 2.37 Mb.
|
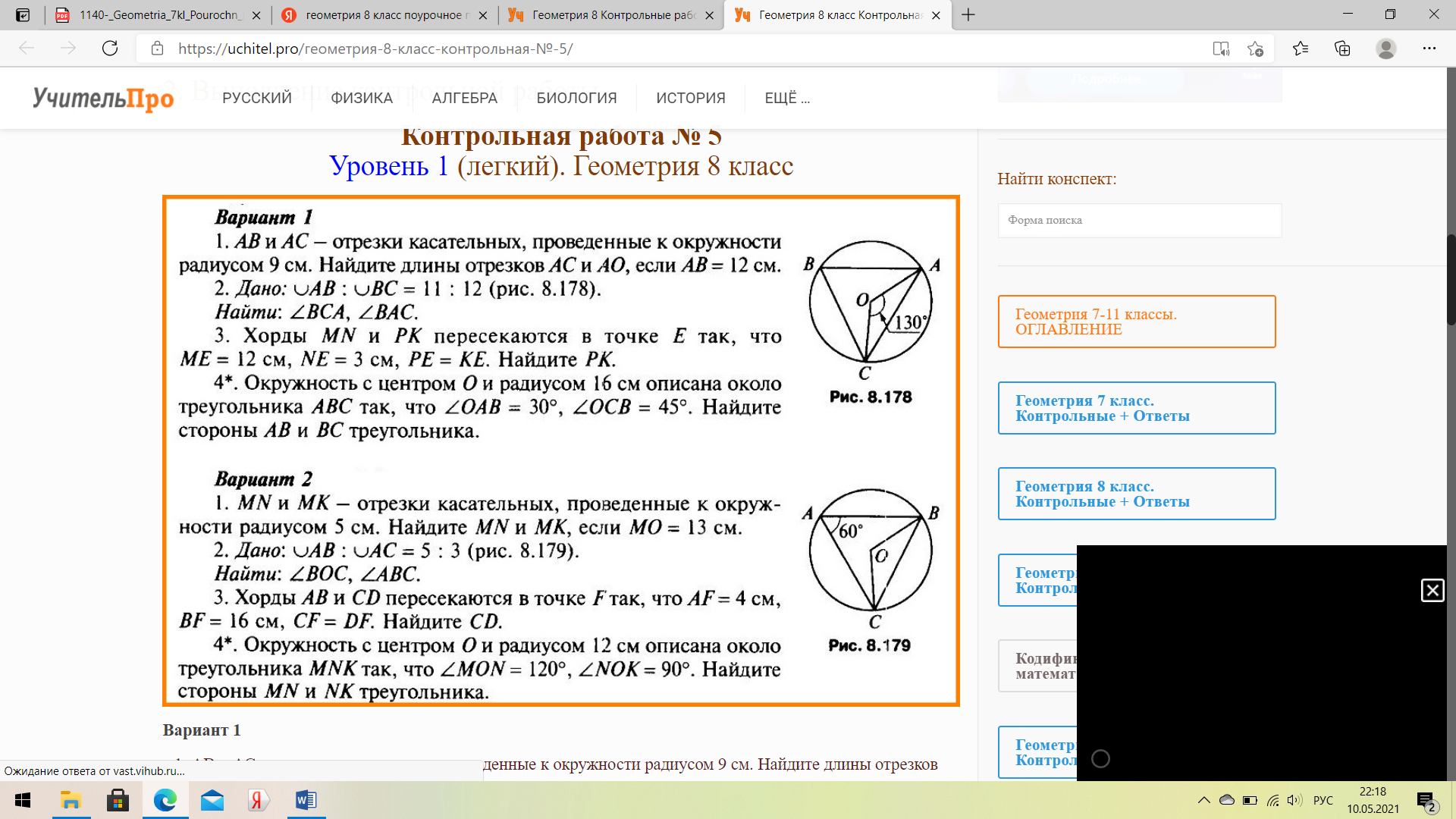  Вариант 1 В треугольник вписана окружность так, что три из шести получившихся отрезков касательных равны 3 см, 4 см, 5 см. Определите вид треугольника. Точки А и В делят окружность с центром О на дуги AMВ и АСВ так, что дуга АСВ на 60° меньше дуги AMВ. AM — диаметр окружности. Найдите углы АМВ, АВМ, АСВ. Хорды АВ и CD пересекаются в точке Е так, что АЕ = 3 см, BE = 36 см, СЕ : DE = 3 : 4. Найдите CD и наименьшее значение радиуса этой окружности. * В равнобедренном треугольнике боковая сторона равна 10 см, а биссектриса, проведенная к основанию, — 8 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. Вариант 2 В прямоугольный треугольник вписана окружность радиусом 2 см так, что один из получившихся отрезков касательных равен 4 см. Найдите стороны треугольника, если его периметр равен 24 см. Точки Е и Н делят окружность с центром О на дуги ЕАН и ЕКН так, что дуга ЕКН на 90° меньше дуги ЕАН, ЕА — диаметр окружности. Найдите углы ЕКА, ЕАН, ЕКН. Хорды MN и РК пересекаются в точке А так, что МА = 3 см, NA = 16 см, РА : КА = 1 : 3. Найдите РК и наименьшее значение радиуса этой окружности. * В равнобедренном треугольнике основание равно 10 см, а высота, проведенная к ней, — 12 см. Найдите радиус окружности, вписанной в этот треугольник, и радиус окружности, описанной около этого треугольника. Ответы на Вариант 1№ 1). Остроугольный (Примечание: в печатном пособии в данном месте опечатка: вместо остроугольный указано прямоугольный). № 2). ∠AMB = 75°, ∠ABM = 90°, ∠ACB = 105°. (Примечание: в печатном пособии в данном месте опечатка, указаны другие ответы). № 3). CD = 21 см; r = 19,5 см. № 4). г = 3 см, R = 6,25 см. Смотреть указания к РЕШЕНИЮ заданий Варианта 1 Ответы на Вариант 2№ 1). 6 см, 8 см, 10 см. № 2). ∠EKA = 90°, ∠EAH = 67°30′, ∠EKH = 112°30′. № 3). РК = 16 см; r = 9,5 см. № 4). г = 3 см, R = 7 см. Смотреть указания к РЕШЕНИЮ заданий Варианта 2 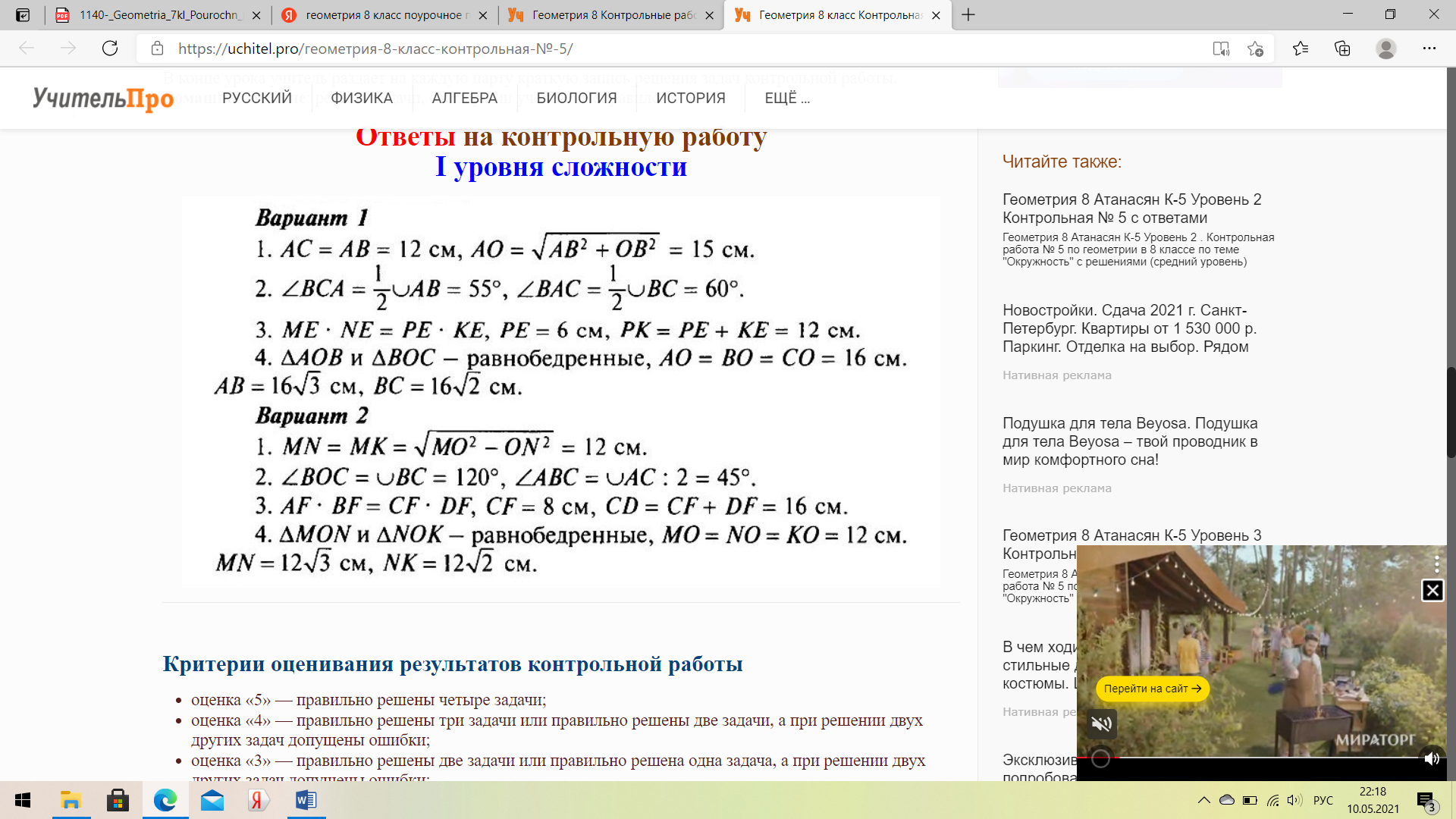 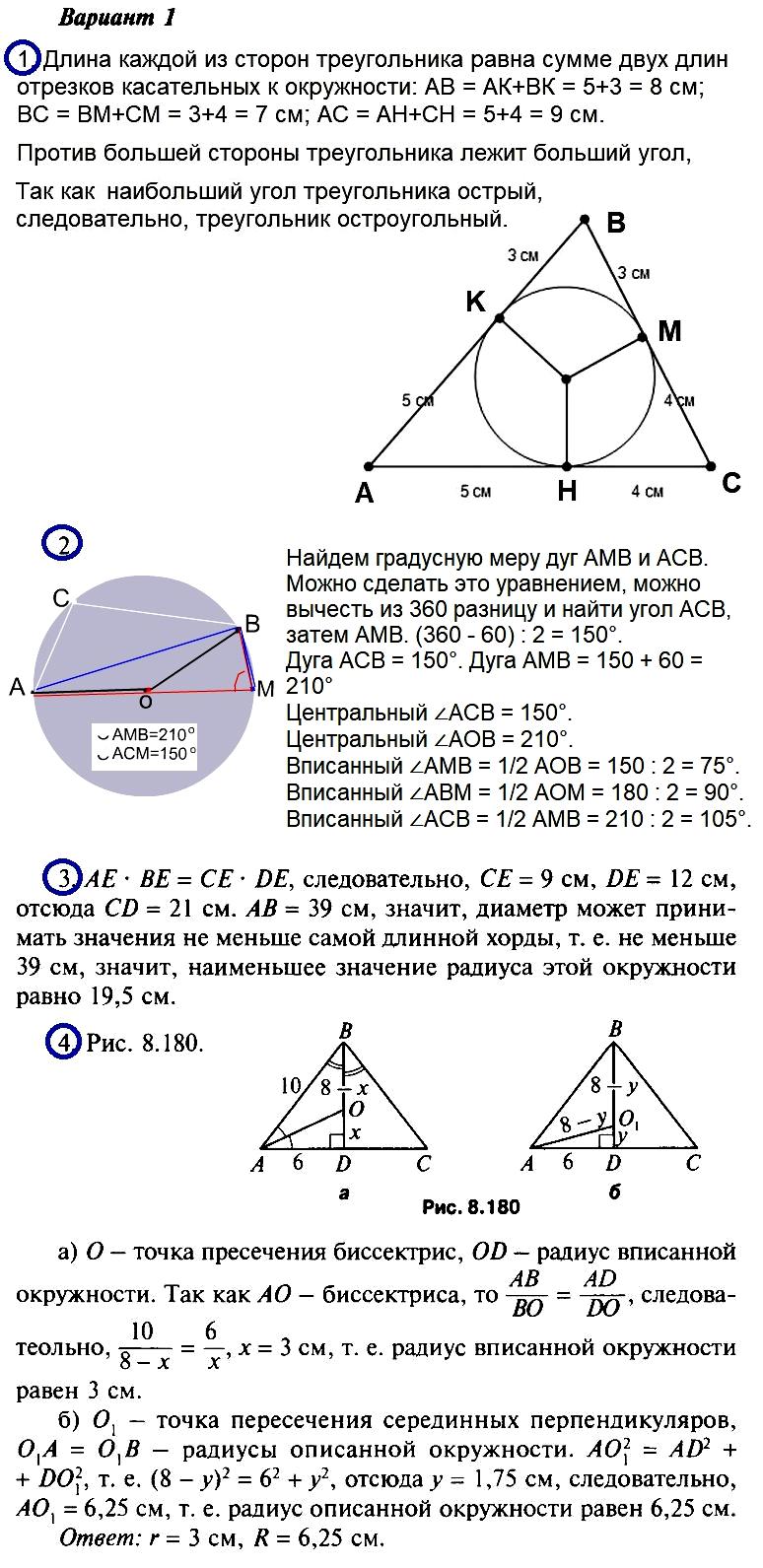 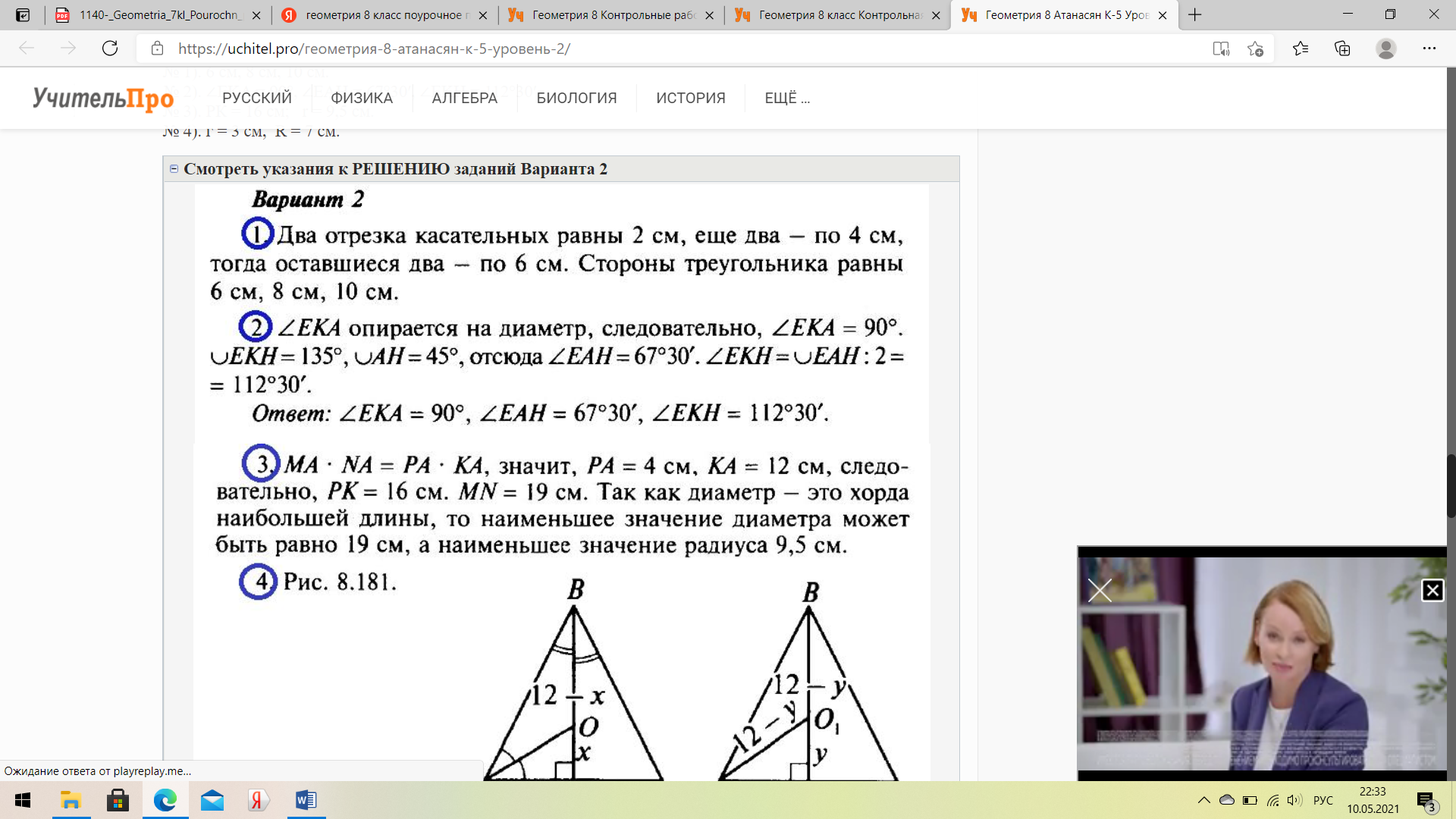  |
