Теория вероятностей и математическая статистика готовые билеты. ТВиМС билеты. 1. Понятие комбинаторики. Виды комбинаций без повторений определения, формулы

• Название: 1. Понятие комбинаторики. Виды комбинаций без повторений определения, формулы
• Анкор: Теория вероятностей и математическая статистика готовые билеты
• Дата: 07.02.2022
• Размер: 469.55 Kb.
• Имя файла: ТВиМС билеты.docx
• Тип: Закон; #354498

1. Понятие комбинаторики. Виды комбинаций без повторений: определения, формулы

Комбинаторика - раздел математики, который изучает, сколько различных комбинаций, подчиненных тем или иным законам или условиям можно составить из объектов. Изучает задачи выбора элементов из заданного множества и размещения в каком либо порядке.

Перестановками называют комбинации, состоящие из одних и тех же n различных элементов и отличающиеся только порядком их расположения. Число всех возможных перестановок Р_n = n!

Размещениями называют комбинации, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений .

Сочетаниями называют комбинации, составленные из nразличных элементов по m элементов, которые отличаются хотя бы одним элементом. Число сочетаний .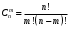

2. Комбинаторные принципы сложения и произведения. Виды комбинаций с повторениями: определения, формулы.

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Р(А + В) = Р(А) + Р(В). ИЛИ

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А –деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. И

Перестановка(опр из в1)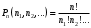

Размещение Ā^r_n=n^r

Сочетание Č^r_n=(n+r-1)!/r!(n-1)!

Каждый объект может участвовать несколько раз/среди которых могут быть одинаковые
3. Понятие случайного события. Совместные и несовместные события. Равновозможные события. Классическое определение вероятности.

Случайное событие - любой факт, который в результате испытания может произойти или не произойти. Это результат испытания. Испытание - эксперимент, выполнение определённого комплекса условий, в котором наблюдается то или иное явление (выпадение кости).

Совместные - называются события А и В, если они не могут произойти одновременно. A*B≠0. В противном случае они называются несовместными.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое (появление герба).

Классическое определение вероятности: Говорят, что совокупность событий образует полную группу событий, для испытания результатом, которого становится хотя бы одно из них. Р(A) = m/n.

4. Понятие случайного события. Виды событий: достоверное, невозможное, равносильное. Классическое определение вероятности. Свойства вероятности события.
Случайное событие - любой факт, который в результате испытания может произойти или не произойти. Это результат испытания. Испытание - эксперимент, выполнение определённого комплекса условий, в котором наблюдается то или иное явление (выпадение кости).

Достоверным называют событие, которое обязательно произойдет, если будет осуществлена определенная совокупность условий S.

Невозможным называют событие, которое заведомо не произойдет, если будет осуществлена совокупность условий S.

События называют равновозможными, если есть основания считать, что ни одно из них не является более возможным, чем другое (появление герба).

Классическое определение вероятности: Говорят, что совокупность событий образует полную группу событий, для испытания результатом, которого становится хотя бы одно из них.

Свойства вероятности события: 1. Вероятность достоверного события равна 1. Р(Ω) = m/n=1; 2. Вероятность невозможного события равна 0. Р(ø)=m/n=0/n=0; 3. Вероятность случайного события есть число положительное между 0 и 1. 0<=P(A)<=1.
5. Вероятность противоположных событий. Произведение событий, сумма событий. Условная вероятность. Теорема умножения.

Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято обозначать .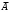

Произведением двух событий А и В называют событие АВ, состоящее в совместном появлении (совмещении) этих событий. Например, если А –деталь годная, В – деталь окрашенная, то АВ – деталь годна и окрашена.

Суммой А + В двух событий А и В называют событие, состоящее в появлении события А, или события В, или обоих этих событий. Например, если из орудия произведены два выстрела и А – попадание при первом выстреле, В – попадание при втором выстреле, то А + В – попадание при первом выстреле, или при втором, или в обоих выстрелах.
Условной вероятностью Р_А(В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило. В урне 3 белых и 3 черных шара. Из урны дважды вынимают по одному шару, не возвращая их обратно. Найти вероятность появления белого шара при втором испытании (событие В), если при первом испытании был извлечен черный шар (событие А).

Теорема умножения: Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило: Р(АВ) = Р(А) Р_А(В). Доказательство. По определению условной вероятности, Р_А(В) = Р(АВ)/ Р(А). Отсюда Р(АВ) = Р(А) Р_А(В).

Для независимых событий теорема умножения Р(АВ) = Р(А) Р_А(В) имеет вид Р(АВ) = Р(А) Р(В),
6. Независимые события. Сумма событий. Формулы Байеса.
Событие В называют независимым от события А, если появление события А не изменяет вероятности события В, т.е. если условная вероятность события В равна его безусловной вероятности: Р_А(В) = Р(В). Подставив (2.12) в соотношение (в5), получим Р(А)Р(В) = Р(В)Р_В(А). Отсюда Р_В(А) = Р(А).

Суммой нескольких событий называют событие, которое состоит в появлении хотя бы одного из этих событий. Например, событие А + В + С состоит в появлении одного из следующих событий: А, В, С, А и В, А и С, В и С, А и В и С.

Теорема Байеса: Вероятность события А, которое может наступить лишь при условии появления одного из несовместных событий Н₁, Н₂,…, Н_n, образующих полную группу, равна сумме произведений вероятностей каждого из этих событий на соответствующую условную вероятность события А: Р(А) = Р(Н₁)Р(А/Н₁) + Р(Н₂)Р(А/Н₂) + ... ... + Р(Н_n)Р(А/Н_n) = .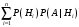
7. Понятие схемы Бернулли. Формула Бернулли. Локальная и интегральная формулы Myавра-Лапласа в схеме Бернулли.
Схема Бернулли - последовательность n независмых испытаний, в каждом из котрых может произойти некоторое событие А (его называют успехом) с вероятностью Р(А) = р или противоположное ему событие 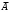(его называют неудачей) с вероятностью .

Формула Бернулли:

Локальная теорема Лапласа. Если вероятность р появления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(m) того, что событие А появится в n испытаниях ровно m раз, приближенно равна (тем точнее, чем больше n) значению функции , где . Выражение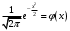 называется функцией Гаусса.

Интегральная теорема Муавра-Лапласа. Если вероятность р наступления события А в каждом испытании постоянна и отлична от нуля и единицы, то вероятность P_n(k₁  m k₂) того, что событие А появится в n испытаниях от k₁ до k₂ раз, может быть найдена по приближенной формул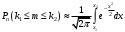е , где . .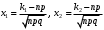

8. Понятие случайной величины. Понятие дискретной случайной величины (ДСВ). Примеры ДСВ. Закон распределения ДСВ.

Случайная величина - величина, которая в результате опыта принимает то или иное значение, причем неизвестно заранее, какое именно. X, Y, Z

Случайной величиной Х называется числовая функция, определенная на пространстве элементарных событий (ПЭС) , которая каждому элементарному событию  ставит в соответствие число Х(), то есть Х = Х(), (или Х = f()).

Дискретной (прерывной) называют случайную величину (сокращено д.с.в.), которая принимает отдельные, счетные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.

Пример. Опыт состоит в бросании монеты 2 раза. На ПЭС  = {₁, ₂, ₃, ₄}, где ₁ = ГГ, ₂ = ГР, ₃ = РГ, ₄ = РР, можно рассмотреть с.в. Х – число появлений герба. С.в. Х является функцией от элементарного события _i: Х(₁) = 2, Х(₂) = 1, Х(₃) = 1, Х(₄) = 0; Х – д.с.в. со значениями х₁ = 0, х₂ = 1, х₃ = 0.

Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.

Пусть Х – д.с.в., которая принимает значения х₁, х₂, …, x_n,… (множество этих значений конечно или счетно) с некоторой вероятностью p_i, где i = 1,2,…, n,… Закон распределения д.с.в. удобно задавать с помощью формулы p_i = P{X = x_i}где i = 1,2,…, n,…, определяющей вероятность того, что в результате опыта с.в. Х примет значение x_i. Для д.с.в. Х закон распределения может быть задан в виде таблицы распределения:
9. Независимые случайные величины. Функции от ДСВ. Методика записи распределения функции от одной ДСВ. Методика записи распределения функции от двух независимых ДСВ.

Две СВ называются независимыми, если закон распределения одной СВ не изменяется от того, какие возможные значения принесла другая другая СВ. Несколько с.в. называют взаимно независимыми, если закон распределения любой из них не зависит от того, какие возможные значения приняли остальные величины.

Сумма х и у, события Х=х, У=у является независимым, т.к. события Х=х и У=у- независимые то по теореме произведения независимых событий. Р(Х=х, У=у)=Р(Х=х)*Р(У=у)

Произведением КХ случайной величины Х на постоянную К называют СВ, которая принимает значения К*Хi, i=i,n с теми же вероятностями pi.(умножается значение на строку х)

Суммой СВ Х и У называют случайную величину, которая принимает все возможные значения Xi+Yi с вероятностями того, что СВ Х примет значение xi СВ. У примет значение yi.

Разностью СВ Хи У называют СВ, которая принимает все возможные значения вида xi-yi с вероятностью pij, того, что СВ примет значение xi. СВ примет значение yj.

Произведение СВ Х и У называют СВ, которая принимает значения вида xi*yj с вероятностью pij того, что СВ примет xi. СВ У примет значение yj. Т.к. СВ Х и У - независимые, то по теореме умножения вероятностей Pij=P(X=xi)*P(Y=yi)=pi*pj
10. Числовые характеристики ДСВ: математическое ожидание, дисперсия, среднее квадратическое отклонение. Определение, сущность, свойства

Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности. М(X) = x₁ р₁ + x₂р₂ + ... + х_nр_n.

Зам1 Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина.

Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Свойство 1. Математическое ожидание постоянной величины равно самой постоянной: М(С) = С. М(С) = С1 = C

Свойство 2. Постоянный множитель можно выносить за знак математического ожидания: М(СХ) = СМ(X).

Свойство 3. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(XY) = M(X)M(Y).

Математическое ожидание М(X) числа появлений события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании М(X) = nр.
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонения случайной величины от ее математического ожидания: (X) = М[X – М(X)]²

Теорема. Дисперсия равна разности между математическим ожиданием квадрата случайной величины X и квадратом ее математического ожидания: D(X) = M(X²) – [М(X)]².

Свойство 1. Дисперсия постоянной величины С равна нулю: D(С) = 0.

Свойство 2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат: D(СX) = C² D(X).

Свойство 3. Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин: D(X + Y) =D(X) + D(Y)

Свойство 4. Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D(X – Y) =D(X) + D(Y).

Средним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии: .
11. Понятие биномиального распределения, характеристики биномиального распределения. Распределения Пуассона.

Биномиальным называют распределение вероятностей, определяемое формулой Бернулли. Закон назван «биномиальным» потому, что правую часть в равенстве можно рассматривать как общий член разложения бинома Ньютона:

.

Таким образом, первый член разложения рⁿ определяет вероятность наступления рассматриваемого события n раз в n независимых испытаниях; второй член nр^n-1q определяет вероятность наступления события n – 1 раз; ...; последний член qⁿ определяет вероятность того, что событие не появится ни разу.
Пуассона. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Для определения вероятности k появлений события в этих испытаниях используют формулу Бернулли. Если же n велико, то пользуются асимптотической формулой Лапласа. Однако эта формула непригодна, если вероятность события мала (p  0,1). В этих случаях (n велико, р мало) прибегают к асимптотической формуле Пуассона.

Как было показано при изучении схемы Бернулли, эта вероятность равна . nр = .
12. Понятие геометрического распределения, характеристики геометрического распределения.

Пусть производятся независимые испытания, в каждом из которых вероятность появления события А равна р (0< р < 1) и, следовательно, вероятность его непоявления q = 1 – р. Испытания заканчиваются, как только появится событие А. Таким образом, если событие А появилось в k-м испытании, то в предшествующих k – 1 испытаниях оно не появлялось.

Обозначим через X дискретную случайную величину – число испытаний, которые нужно провести до первого появления события А. Очевидно, возможными значениями X являются натуральные числа: x₁ = 1, x₂ =2, ...

Пусть в первых k – 1 испытаниях событие А не наступило, а в k-м испытании появилось. Вероятность этого «сложного события», по теореме умножения вероятностей независимых событий, .

Из орудия производится стрельба по цели до первого попадания. Вероятность попадания в цель р = 0,6. Найти вероятность того, что попадание произойдет при третьем выстреле.
13. Понятие НСВ. Равномерное распределение. Геометрическое определение вероятности.

Функцией распределения называют функцию F(х), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х, т.е. .

Уточним определение непрерывной случайной величины: случайную величину называют непрерывной, если ее функция распределения есть непрерывная, кусочно-дифференцируемая функция с непрерывной производной.

Свойство 1. F(х) ограничена, то есть значения функции распределения принадлежат отрезку [0, 1]: 0  F(х)  1

Свойство 2. F(х) – неубыв. функция на R, т.е. F(x₂)  F(x₁), если х₂ > х₁

Свойство 3. Если возможные значения случайной величины принадлежат интервалу (а, b), то: 1) F(x) = 0 при х  а; 2) F(x) = 1 при х  b.



Распределение вероятностей называют равномерным, если на интервале, которому принадлежат все возможные значения случайной величины, плотность распределения сохраняет постоянное значение.
14. Функция плотности НСВ: определение, свойства. Функция плотности для равномерно распределённой НСВ. Интегральная функция распределения НСВ: определение, свойства, её связь с функцией плотности.

Плотностью распределения вероятностей непрерывной случайной величины X называют функцию f(х) – первую производную от функции распределения F(х): f(х) = F' (х).

Установим вероятностный смысл плотности распределения. Из определения производной следует

Плотность распределения есть предел отношения вероятности попадания с.в. в промежуток к длине х этого промежутка, когда х стремится к нулю. Из равенства (10.1) следует, что .

Вероятностный смысл равенства .

Отметим, что плотность f(х) аналогична таким понятиям, как плотность распределения масс на оси абсцисс или плотность тока в теории электричества.
15. Методика вычисления математического ожидания, дисперсии, среднеквадратического отклонения НСВ по её функции плотности. Медиана НСВ: определение, методика нахождения.

Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а, b], называют определенный интеграл . Если возможные значения принадлежат всей оси Ох, то .

Дисперсией непрерывной случайной величины называют математическое ожидание квадрата ее отклонения.

Если возможные значения X принадлежат отрезку [а, b], то ;

Среднее кеадратическое отклонение непрерывной случайной величины определяется, как и для величины дискретной, равенством .

С помощью функции распределения F(x) равенство (11.3) можно записать в виде F(М_еХ) = 1 – F(М_еХ)

Медианой М_еХ н.с.в. Х называется такое ее значение х_р, для которого , то есть одинаково вероятно, окажется ли с.в. Х меньше х_р или больше х_р.
16. Определение и функция плотности нормально распределённой НСВ. Кривая Гаусса и ее свойства. Интегральная функция распределения нормально распределенной НСВ.

Главная особенность закона Гаусса состоит в том, что он является предельным, к которому приближаются, при определенных условиях, другие законы распределения.

Нормальным называют распределение вероятностей непрерывной случайной величины, которое описывается плотностью .

1. 
   По определению математического ожидания непрерывной случайной величины, .
   
2. 
   По определению дисперсии непрерывной случайной величины, учитывая, что М(X) = а, имеем .
   
3. 
   Следовательно, .
   

Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины X по абсолютной величине меньше заданного положительного числа , т.е. требуется найти вероятность осуществления неравенства |Х – а| < .
17. Определение и функция плотности показательно распределенной НСВ. Интегральная функция распределения показательно распределенной НСВ. Характеристики показательно распределенной НСВ.

Найдем вероятность попадания в интервал (а, и) непрерывной случайной величины X, которая распределена по показательному закону, заданному функцией распределения .

Используем формулу (??) . Учитывая, что , , получим . Найдем математическое ожидание: .

Интегрируя по частям, получим .

Найдем дисперсию: .

Интегрируя по частям, получим .

Следовательно, . Найдем среднее квадратическое отклонение, для чего извлечем квадратный корень из дисперсии: .

19. Понятие точечной оценки, Понятие интервальной оценки. 20. Надежность доверительного интервала.

Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, точечные. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, т.е. приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.

Интервальной называют оценку, которая определяется двумя числами - концами интервала. Интервальные оценки позволяют установить точность и надежность оценок (смысл этих понятий выясняется ниже).

Пусть найденная по данным выборки статистическая характеристика служит оценкой неизвестного параметра Ө. Будем считать Ө постоянным числом (Ө может быть и случайной величиной). Ясно, что Ө* тем точнее определяет параметр Ө, чем меньше абсолютная величина разности | Ө - Ө*|. Другими словами, если> Ө и |Ө-Ө| < б, то чем меньше б, тем оценка точнее. Таким образом, положительное число б характеризует точность оценки.

Однако статистические методы не позволяют категорически утверждать, что оценка Ө* удовлетворяет неравенству | Ө - Ө*| < б; можно лишь говорить о вероятности ү, с которой это неравенство осуществляется.

Надежностью (доверительной вероятностью) оценки Ө по Ө* называют вероятность ү, с которой осуществляется неравенство | Ө - Ө*| < б. Обычно надежность оценки задается наперед, причем в качестве ү берут число, близкое к единице. Наиболее часто задают надежность, равную 0,95; 0,99 и 0,999.

21 Интервальная оценка математического ожидания нормального распределения при известной дисперсии.