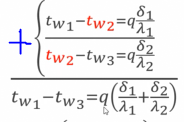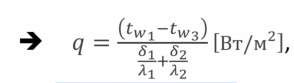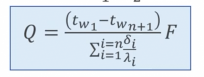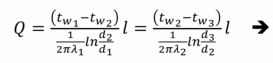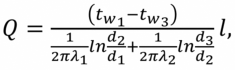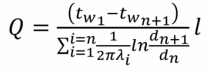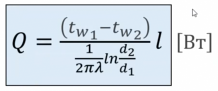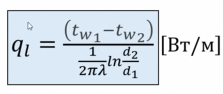эКЗАМЕНАЦИОННЫЕ ВОПРОСЫ ПО ТЕПЛОТЕХНИКЕ. Экзамен_вопрос_ТЕПЛОТЕХНИКА. 1. Понятие о сопле и диффузоре. Истечение из суживающегося сопла. 1
 Скачать 438.59 Kb. Скачать 438.59 Kb.
|
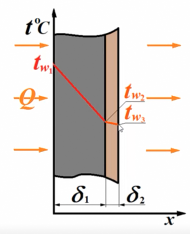
Оглавление1.Понятие о сопле и диффузоре. Истечение из суживающегося сопла. 1 ТЕПЛОПЕРЕДАЧА 1 2.Теплопроводность многослойной плоской стенки. 1 3.Теплопроводность однослойной плоской стенки. 3 1.Теплопроводность сферической стенки. 4 2.Теплопроводность цилиндрической стенки.(многослойной) 4 3.Теплопроводность через однослойную цилиндрическую стенку. 5 4.«Критический диаметр», его определение. 6 5.Излучение. Экспериментальное определение коэффициента лучеиспускания. 6 6.Конвективный теплообмен. Коэффициент теплоотдачи и влияющие на него факторы. 6 7.Конвективный теплообмен: моделирование и использование критериальных уравнений. 7 8.Лучистый теплообмен. Закон Кирхгофа. 7 9.Методика экспериментального определения коэффициента теплопроводности теплоизоляционных материалов. 7 10.Определяющие и определяемые критерии. Критериальные уравнения. Определяющие температуры 7 11.Понятие о температурном градиенте. Передача теплоты теплопроводностью. Уравнение Фурье. 7 12.Теплообмен излучением. 7 13.Теплопередача через многослойную цилиндрическую стенку. Понятие о «критическом диаметре». 7 14.Теплопередача через плоскую многослойную стенку. 7 15.Теплопередача через плоскую стенку. Коэффициент теплопередачи. 7 16.Теплопередача через цилиндрическую стенку. 7 17.Типы теплообменных аппаратов; определение среднего температурного напора. 7 Понятие о сопле и диффузоре. Истечение из суживающегося сопла.ТЕПЛОПЕРЕДАЧАТеплопроводность многослойной плоской стенки.Теплопроводность реализуется на микроуровне за счет переноса теплоты «электронным газом» (металлов) и в результате нестройных упругих колебаний (в диэлектриках). Для процесса теплопроводности характерно (так его можно отличить от другого любого процесса): При теплопроводности отсутствует перемещение в жидкости (конечных масс, объемов и т.д.); В металлах теплопроводность осуществляется электронным газом.
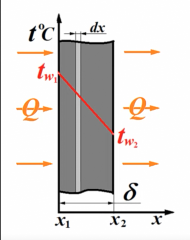
- уравнение Фурье для одномерного потока. Q- тепловой поток (количество теплоты в единицу времени Дж*с) F-площадь поверхности dt/dx – изменение температуры
- толщина tw1- температура тепло принимающей поверхности tw2- температура охлаждающей поверхности Меняем местами tw1 и tw2 => исчезает минус перед дробью, получим:
-[Вт] – расчетная форму определения количества теплоты проходящей через поверхность Разделим тепловой поток на F, получим:
- уравнение плотности теплового потока для многослойной плоской стенки (q- это количество теплоты, передаваемое в 1 ед. времени через один кв. метр поверхности) – это равенство (сколько входит теплоты в стенку столько и выходит) справедливо только для установившегося стационарного процесса! Лямбда λ 1 в уравнении – для первой стенки Лямбда λ 2 – для второй стенки Из формулы для Q, получаем выражение:
- коэффициент теплопроводности (пропорциональности) – есть количество теплоты, передаваемое в 1 ед. времени через 1 кв. метр поверхности стенки толщиной 1 метр, при разности температур в 1К – это физ. смысл коэффициента теплопроводности. Коэффициент теплопроводности λ зависит: от природы вещества (фарфора или сталь, пластмасса и т.д.); от структуры и пористости вещества; зависит от температуры (для большинства металлов – при повышении темп. λ падает, а для строительного материала- при повышении темп. λ тоже повышается) Для пористых веществ, зависит еще от влажности. Материалы обладающие хорошей электропроводность, соответственно имеют и хорошую теплопроводность (золото, медь, платина и т.д.) Из q найдем разность температур, запишем:
tw2 – температура средней поверхности - Просуммируем верхнее и нижнее равенство, сокращаются tw2 и остаются только начальная и конечная температуры, а справа- общая величина q, а в скобках находится сумма термических сопротивлений слоев. Выражаем q и получим:
- формула для определения плотности теплового потока. Где 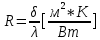 - Термическое сопротивление - Термическое сопротивлениеДля нахождения теплового потока уравнение q домножаем на F, получим:
- формула для нахождения теплового потока. А для нахождения теплоты, еще нужно домножить на время (колич сек.) но уже в Дж.
- формула для нахождения теплового потока с n -слойной стенки. размерность [Вт] Теплопроводность однослойной плоской стенки.Теплопроводность реализуется на микроуровне за счет переноса теплоты «электронным газом» (металлов) и в результате нестройных упругих колебаний (в диэлектриках). Для процесса теплопроводности характерно (так его можно отличить от другого любого процесса): При теплопроводности отсутствует перемещение в жидкости (конечных масс, объемов и т.д.); В металлах теплопроводность осуществляется электронным газом.
- уравнение Фурье для одномерного потока. Q- тепловой поток (количество теплоты в единицу времени Дж*с) F-площадь поверхности dt/dx – изменение температуры
- толщина tw1- температура тепло принимающей поверхности tw2- температура охлаждающей поверхности Меняем местами tw1 и tw2 => исчезает минус перед дробью, получим:
-[Вт] – расчетная форму определения количества теплоты проходящей через поверхность Разделим тепловой поток на F, получим:
- уравнение плотности теплового потока для однослойной плоской стенки (q- это количество теплоты передаваемое в 1 ед. времени через один кв. метр поверхности) Из формулы для Q, получаем выражение:
- коэффициент теплопроводности (пропорциональности) – есть количество теплоты, передаваемое в 1 ед. времени через 1 кв. метр поверхности стенки толщиной 1 метр, при разности температур в 1К – это физ. смысл коэффициента теплопроводности. Коэффициент теплопроводности λ зависит: от природы вещества (фарфора или сталь, пластмасса и т.д.); от структуры и пористости вещества; зависит от температуры (для большинства металлов – при повышении темп. λ падает, а для строительного материала- при повышении темп. λ тоже повышается) Для пористых веществ, зависит еще от влажности. Материалы обладающие хорошей электропроводность, соответственно имеют и хорошую теплопроводность (золото, медь, платина и т.д.) Термическое сопротивление 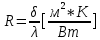 . .Теплопроводность сферической стенки.Теплопроводность цилиндрической стенки.(многослойной)
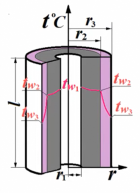
В скобочках стоит сумма термических сопротивлений слоев (первое- для серого, а второе- для фиолетового). Выразим Q, получим:
- расчетная формула формула для нахождения теплового потока.
- формула для нахождения теплового потока(передаваемой теплоты) с n -слойной стенки. Размерность. Теплопроводность через однослойную цилиндрическую стенку.
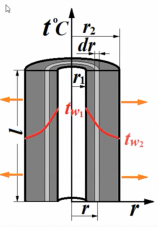
Используем уравнение Фурье применительно к бесконечно тонкому цилиндрическому слою толщиной dr и текущим радиусом r.
Где: 2πrl=F – это есть поверхность бесконечно тонкого слоя.
Меняем местами tw1 и tw2 => чтобы избавиться от знака минус перед дробью, получим:
Т.к. отношение радиусов = отношению диаметров, перепишем:
- расчетная формула для нахождения теплового потока.
- линейная плотность теплового потока – это количество теплоты передаваемая в единицу времени через один погонный (длины) метр трубы.
- разность температур является функцией логарифмической зависимостью (красная на рисунке). «Критический диаметр», его определение.Излучение. Экспериментальное определение коэффициента лучеиспускания.Конвективный теплообмен. Коэффициент теплоотдачи и влияющие на него факторы.Конвективный теплообмен (Теплоотдача) реализуется на макроуровне, в результате переноса теплоты конечными объемами и жидкостями (всеми текучими веществами). Конвективный теплообмен – является следствием совместного проявления конвекции и теплопроводности. Конвекция- это перемещение. Конвекцию различают: Естественную – вызывается перепадом плотности ρ под влиянием разности температур. Вынужденную- вызывается перепадом давления Количество теплоты, которое передается конвективным теплообменом описывается уравнением Ньютона:
Где:
- коэффициент теплоотдачи; Коэффициент теплоотдачи α - это количество теплоты, передаваемое в ед. времени через 1 квадрат. Метр поверхности при разности температур в 1 К. На коэффициент α влияют: Температуры жидкости и ее физические свойства – λ (коэфф. теплопроводности), с (теплоемкость жидкости), ρ (плотности жидкости) и μ (вязкость- чем более вязкое вещество, тем больше конвекция) Режим течения и толщина пограничного слоя
Различают 2 режима течения: Ламинарный (струйный) – все частицы движутся по одинаковым траекториям (не перемешиваются) Турбулентный поток – когда частицы движутся абсолютно беспорядочно Характер движения потока определяется величиной критерием Рейнольдса:
Где: w-скорость потока; l-характерный размер (для трубы- диаметр); ν –кинематическая вязкость Конвективный теплообмен: моделирование и использование критериальных уравнений.Лучистый теплообмен. Закон Кирхгофа.Методика экспериментального определения коэффициента теплопроводности теплоизоляционных материалов.Определяющие и определяемые критерии. Критериальные уравнения. Определяющие температурыПонятие о температурном градиенте. Передача теплоты теплопроводностью. Уравнение Фурье.Теплообмен излучением.Теплопередача через многослойную цилиндрическую стенку. Понятие о «критическом диаметре».Теплопередача через плоскую многослойную стенку.Теплопередача через плоскую стенку. Коэффициент теплопередачи.Теплопередача через цилиндрическую стенку.Типы теплообменных аппаратов; определение среднего температурного напора. |