41. Частотные характеристики последовательного RLC-контура и нормирование его характеристик.
42. Определение полосы пропускания последовательного RLC-контура по его амплитудно-частотной характеристике.
|
43. Включение RL-контура к источнику синусоидального напряжения.
|
44. Прямое преобразование Лапласа. Основные его свойства. Изображения функций: единично- ступенчатой, импульсной, синусоидальной, косинусоидальной, экспоненциальной, линейно-нарастающей. Изображение периодических сигналов.
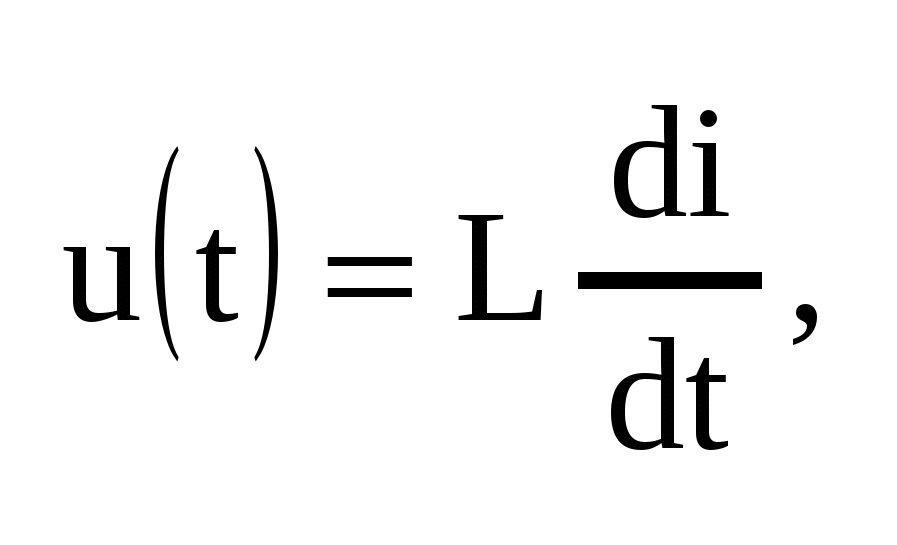 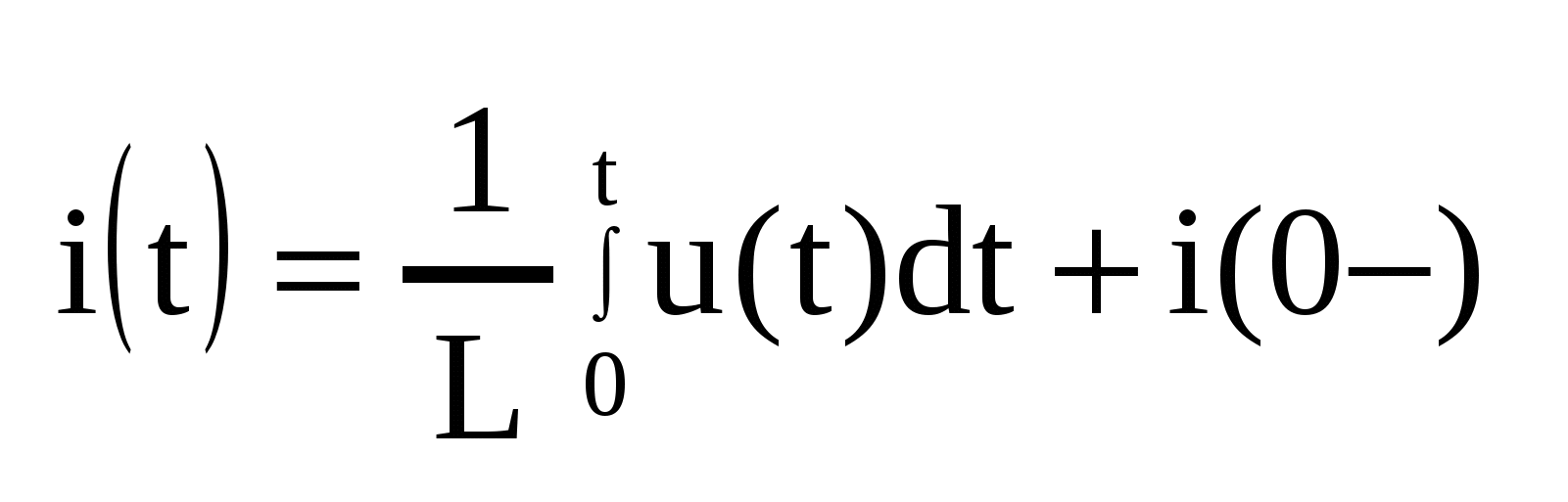
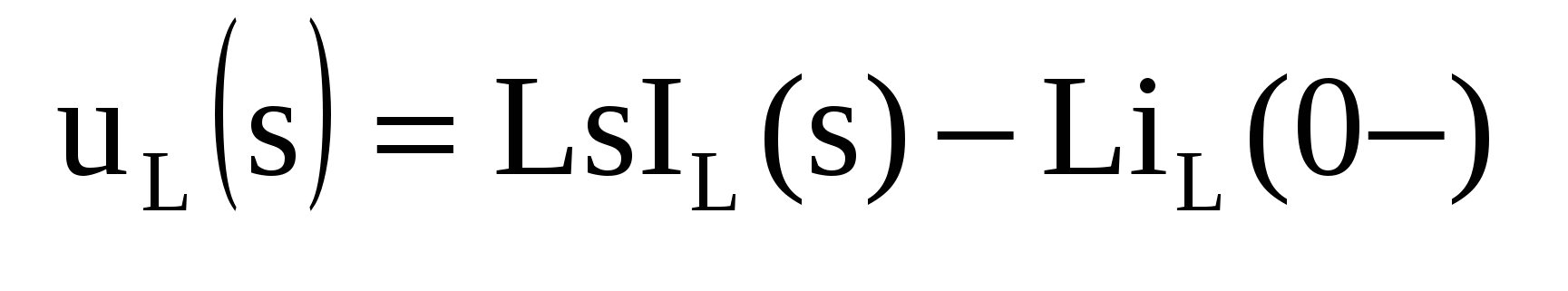
Алгебраическую сумму трактуем как последовательное соединение элементов
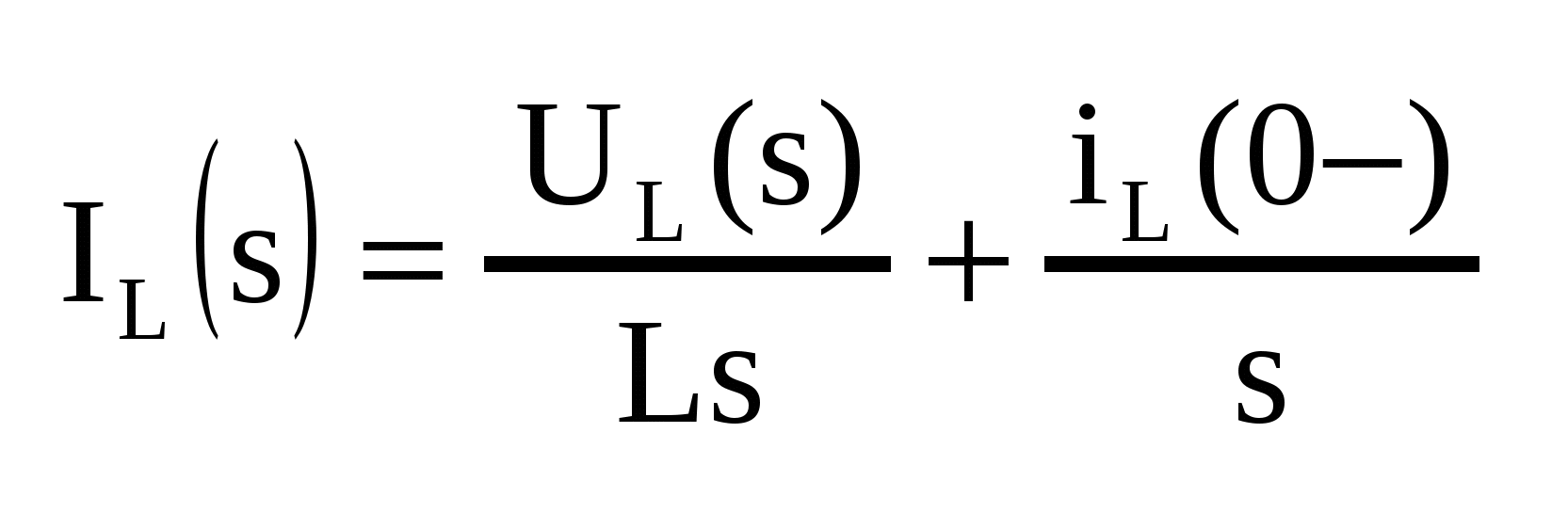
Уравнение параллельного соединения
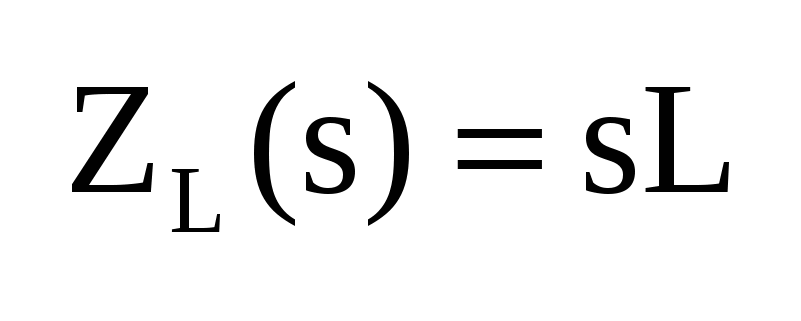 операторное сопротивление L элемента операторное сопротивление L элемента
Вывод: операторные схемы эквивалентны, они соответствуют правилам эквивалентных преобразований ИТ или ИН и удовлетворяет законам Кирхгофа.
|
45. Операторные схемы замещения индуктивного элемента электрической цепи.
|
46. Операторные схемы замещения емкостного элемента электрической цепи.
|
47. Обратное преобразование Лапласа. Теорема разложения для случаев простых вещественных полюсов изображения.
Так как 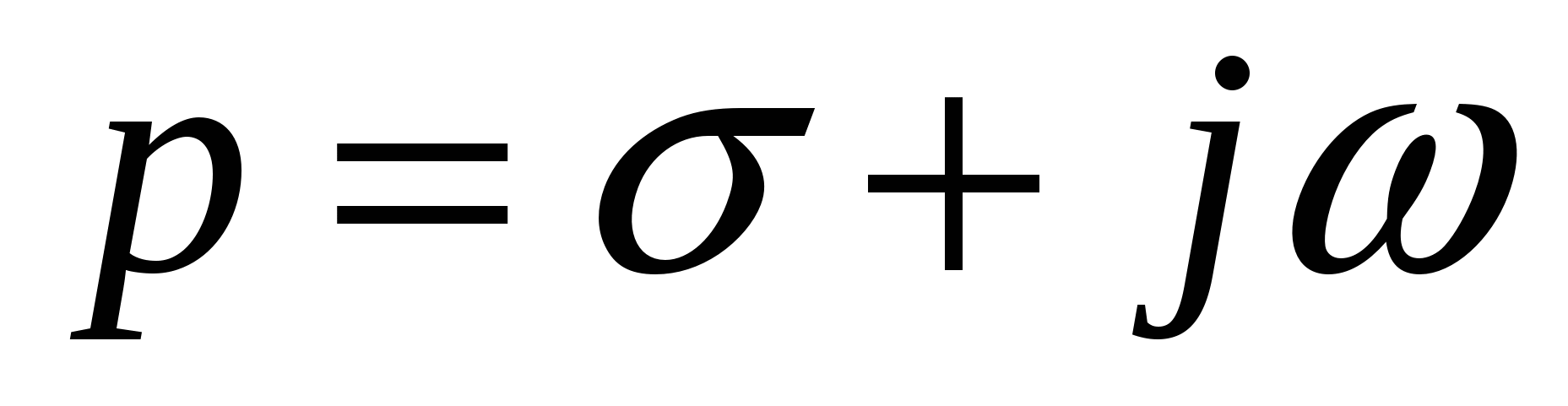 , то , то 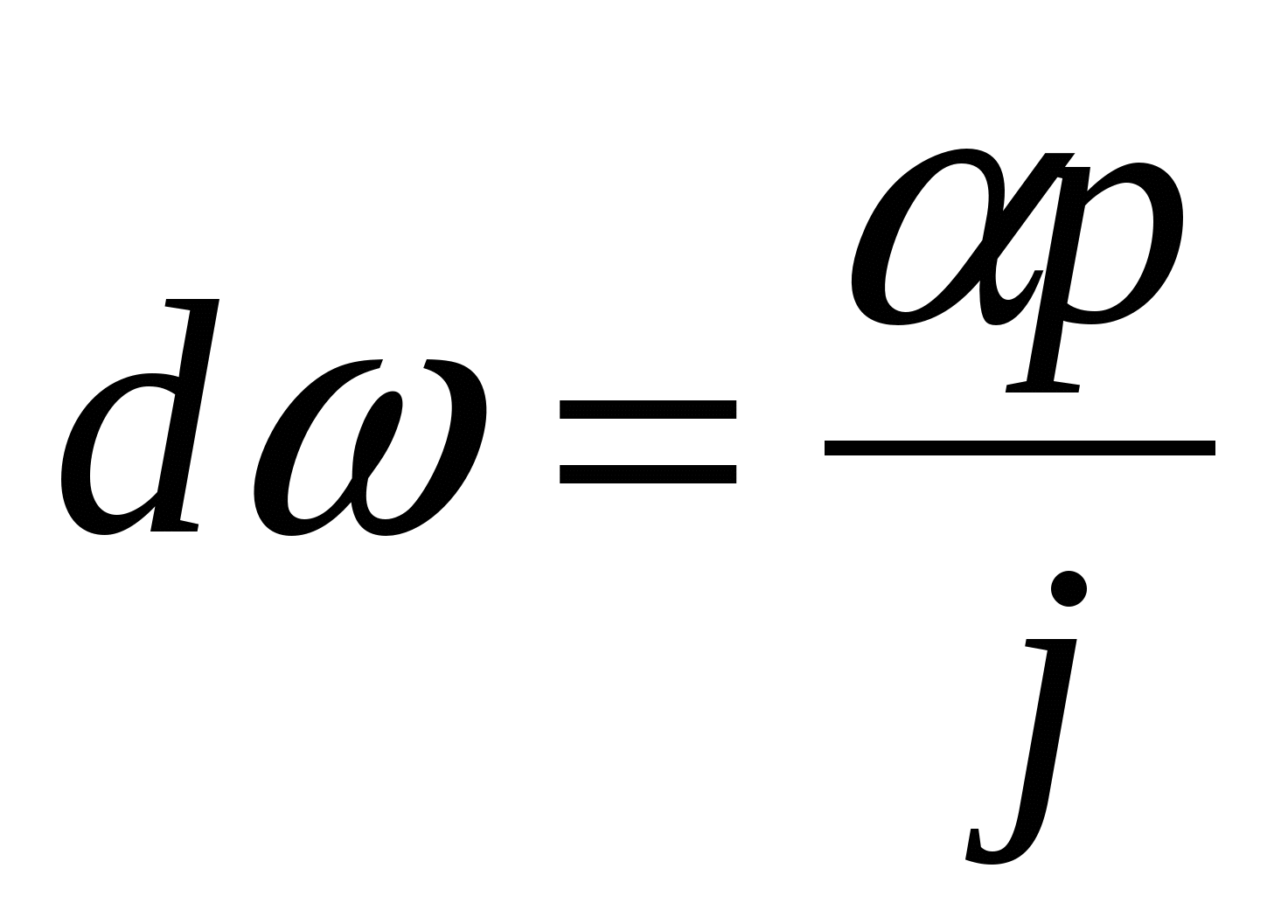 , a пределы интегрирования в при изменении , a пределы интегрирования в при изменении  от от 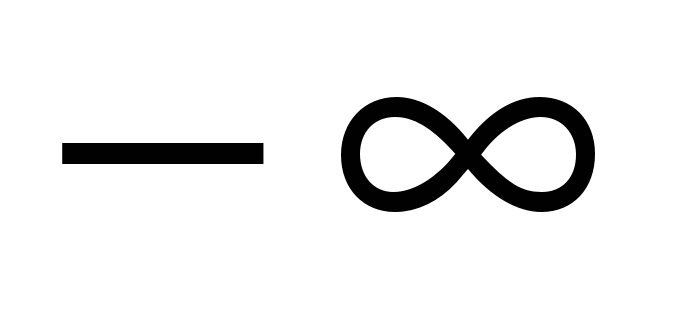 до до 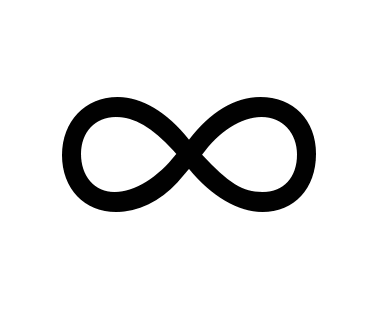 теперь будут соответственно теперь будут соответственно 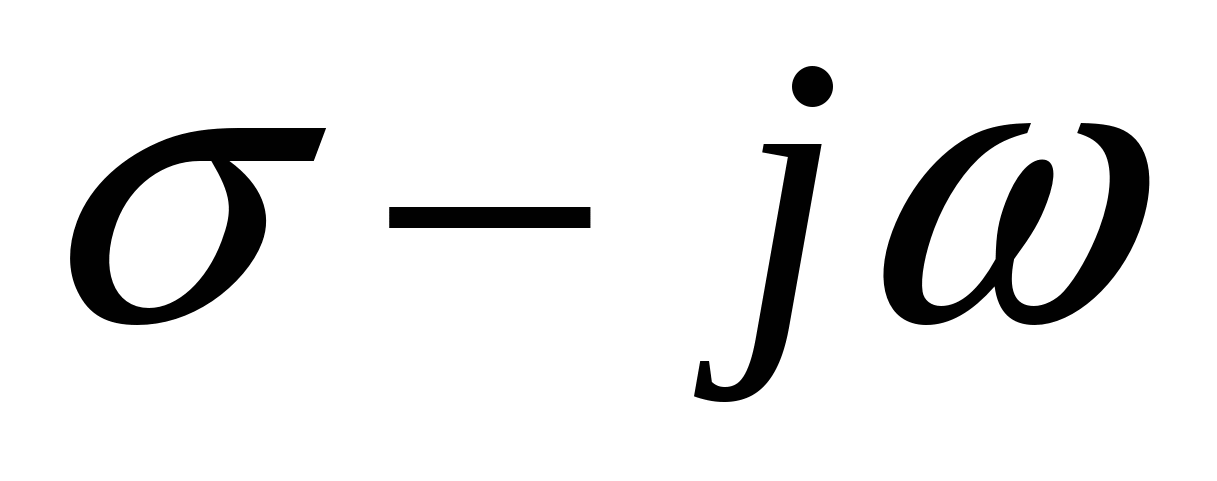 и и 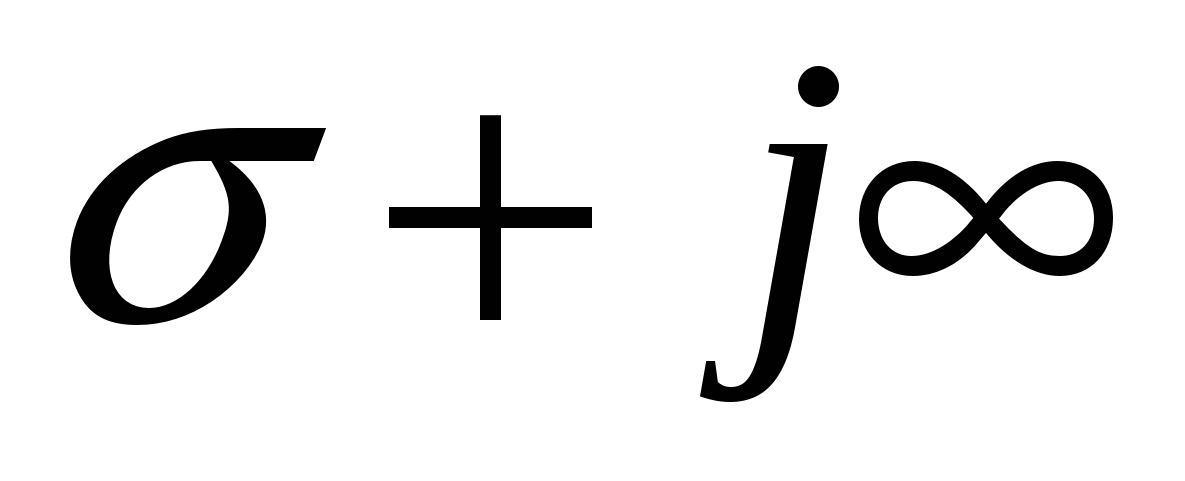 .Тогда получаем: .Тогда получаем:
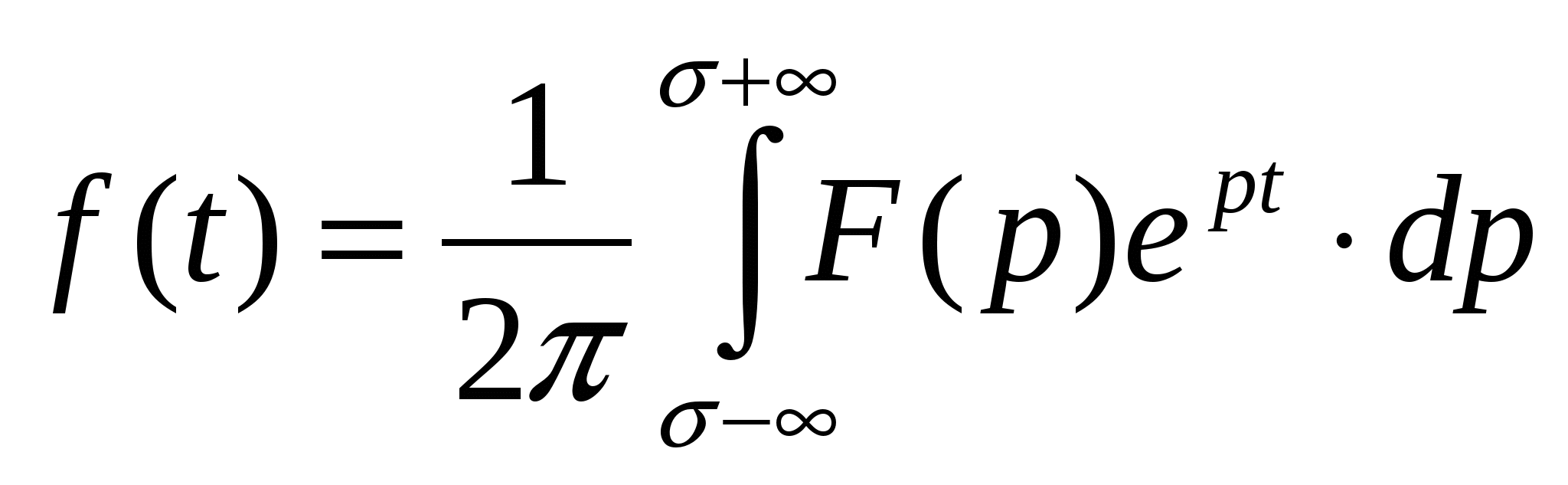 . .
Теорема разложения для Простых вещественных полюсов.
 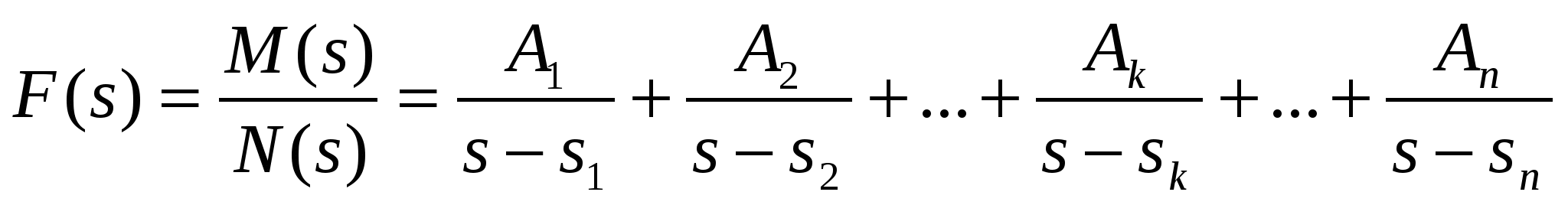 (1) (1)
Коэфиценты А1, А2,…,Аn – вычеты
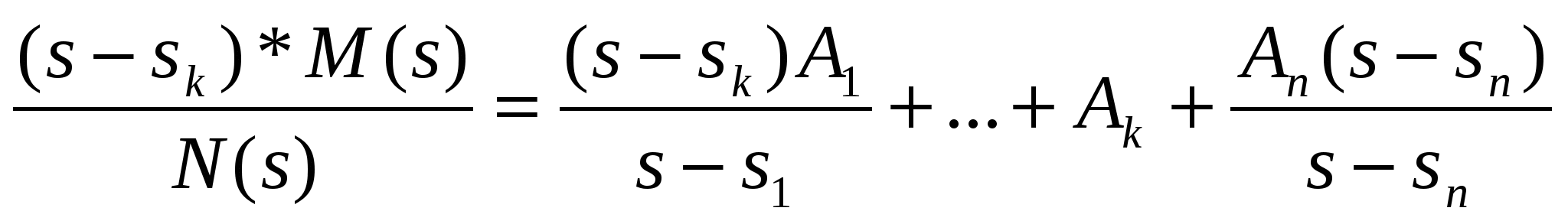 (2) (2)
Положим S=Sk, то есть:
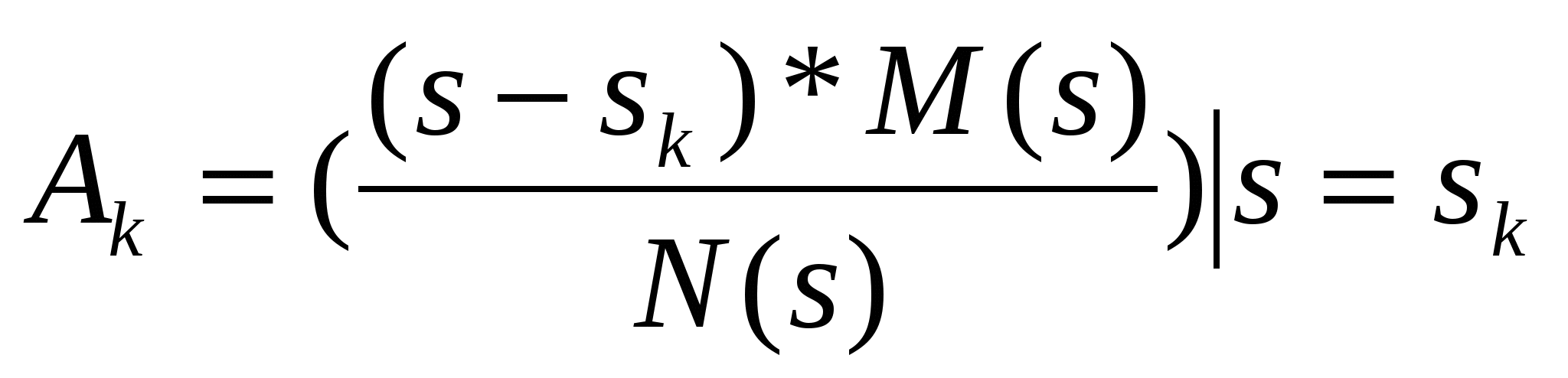
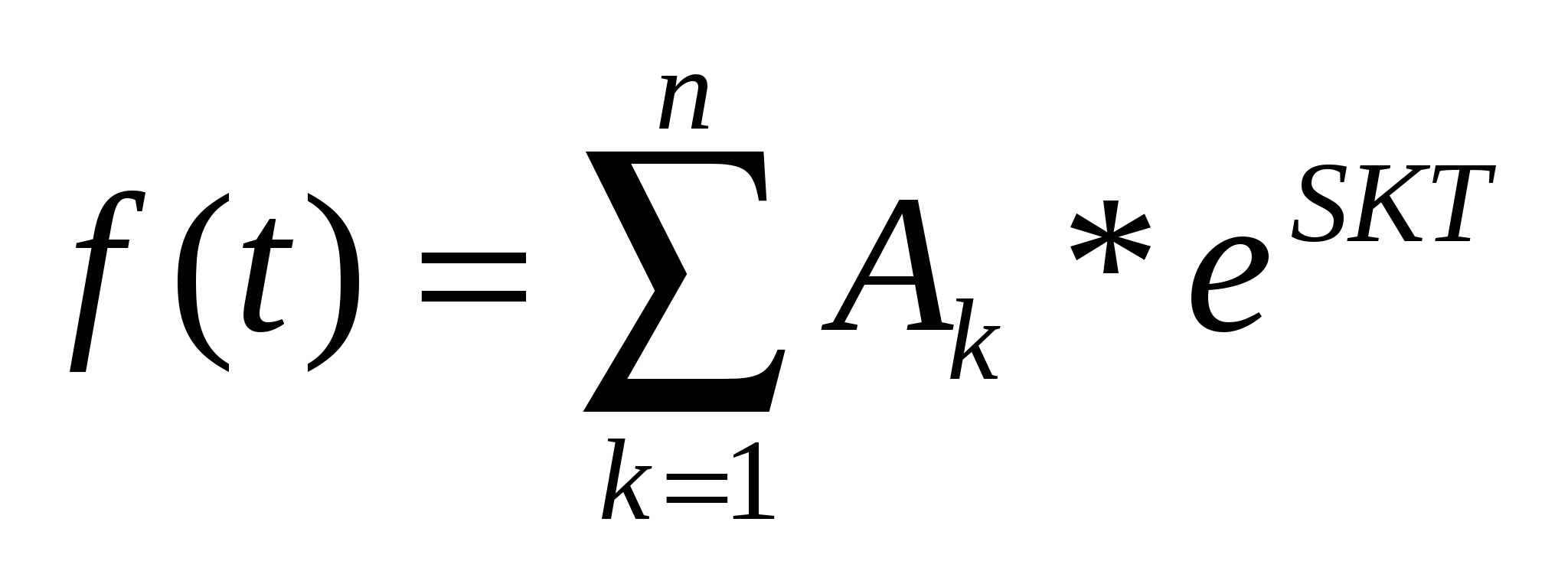 (3) (3)
|
48. Обратное преобразование Лапласа. Теорема разложения для случаев комплексных полюсов изображения.
Так как 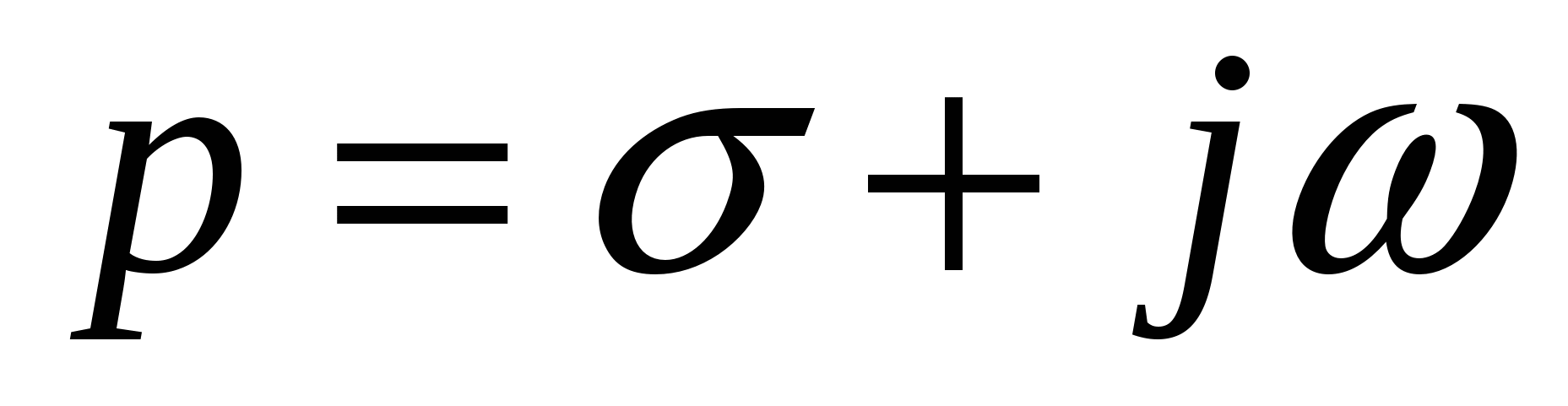 , то , то 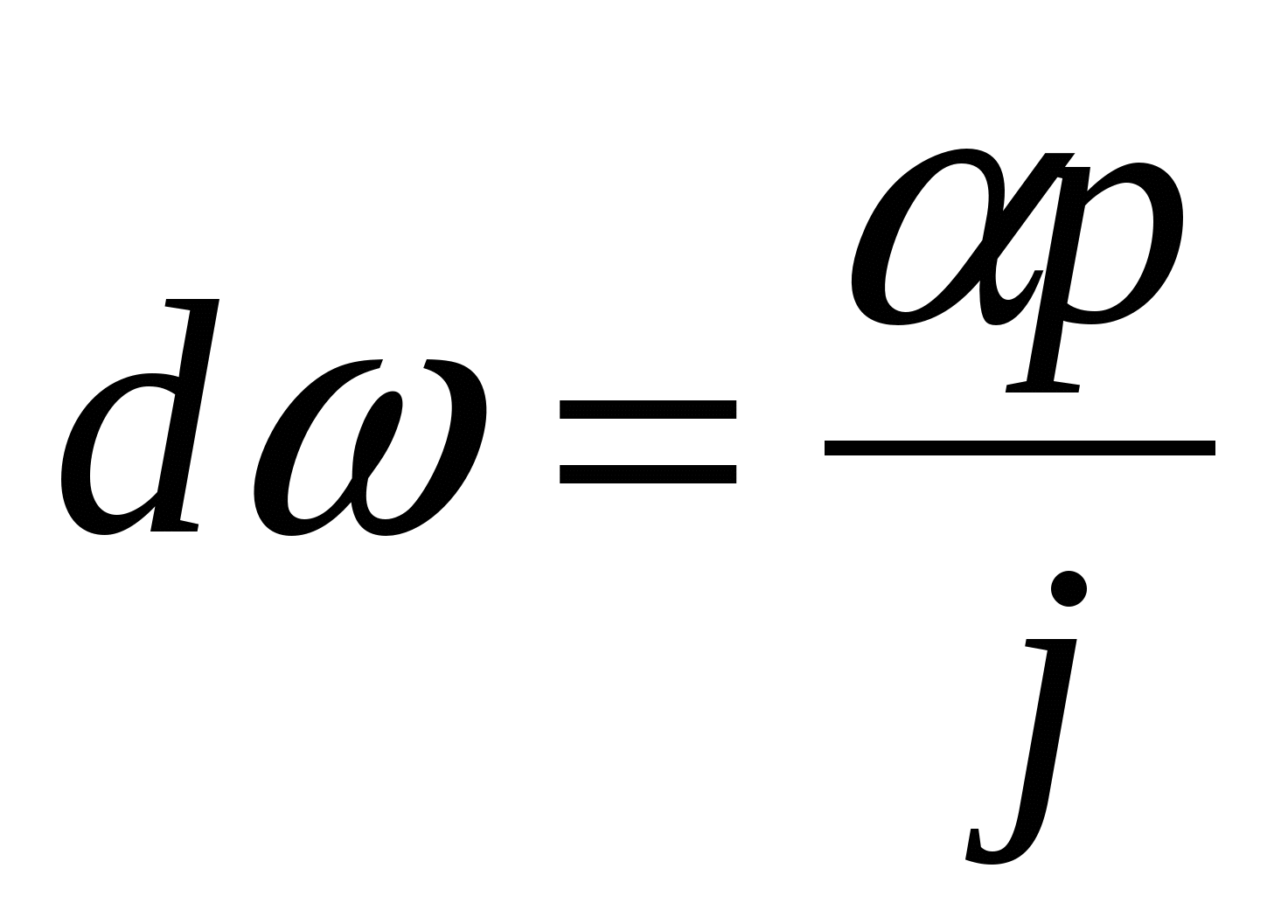 , a пределы интегрирования в при изменении , a пределы интегрирования в при изменении  от от 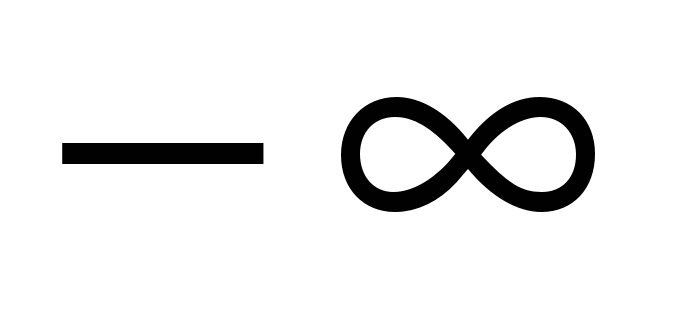 до до 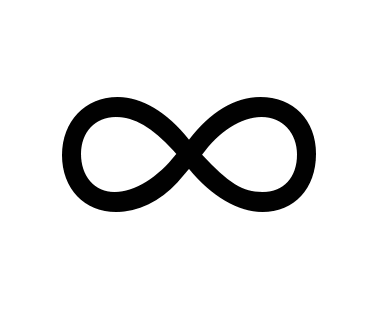 теперь будут соответственно теперь будут соответственно 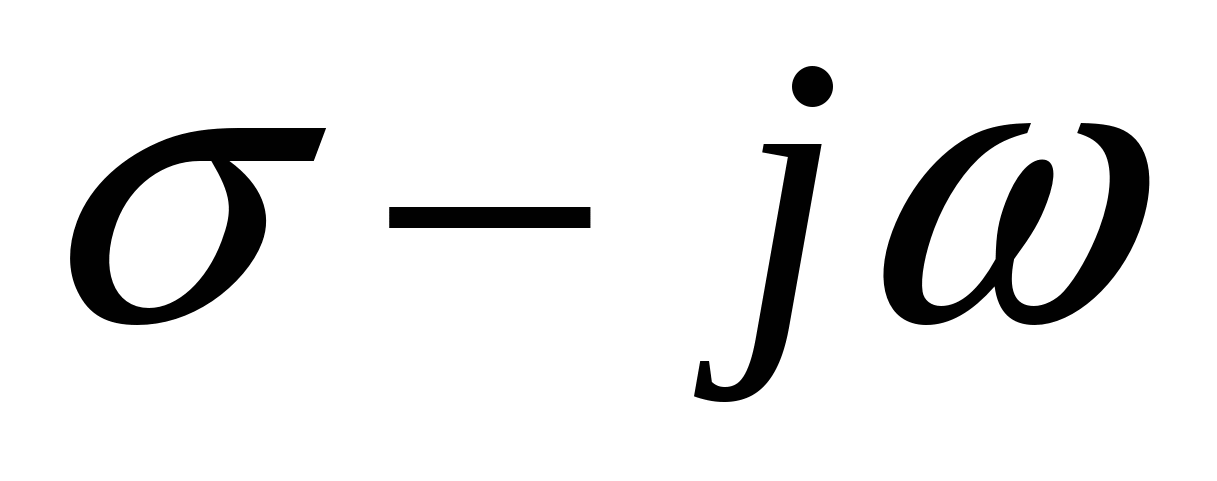 и и 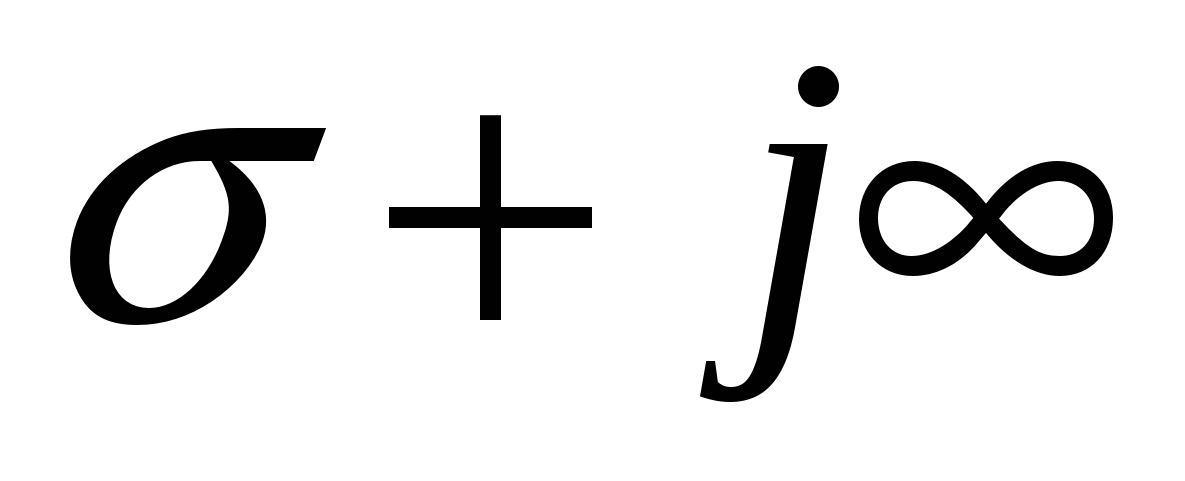 .Тогда получаем: .Тогда получаем:
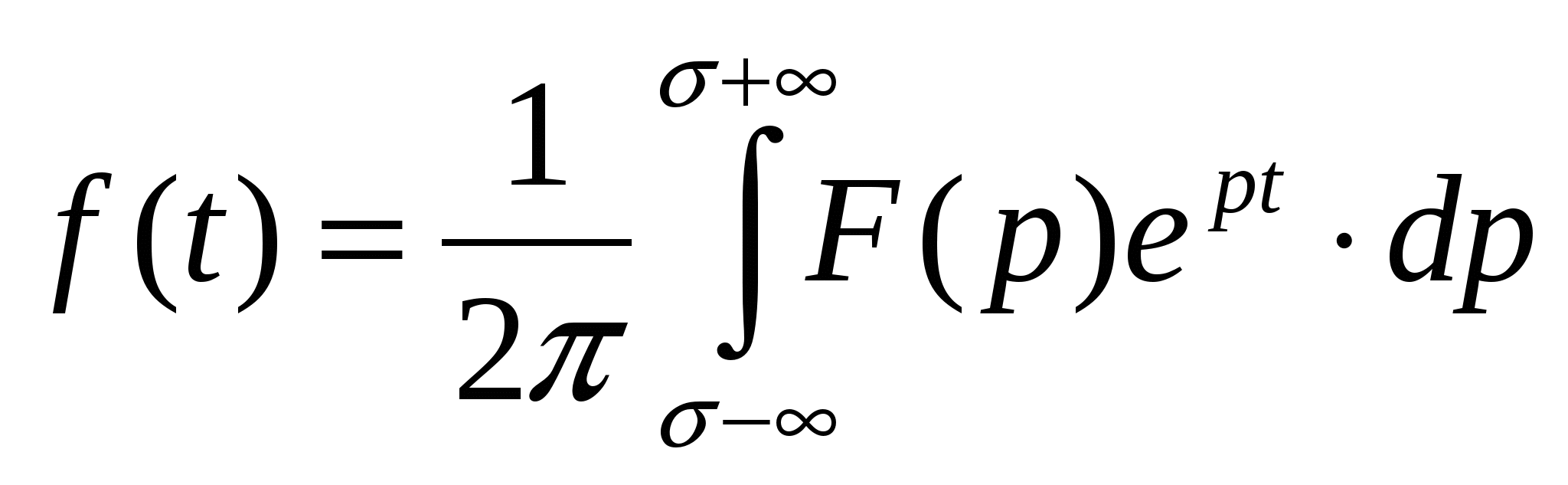 . .
Теорема разложения для Комплексной Байдыыыыыы:
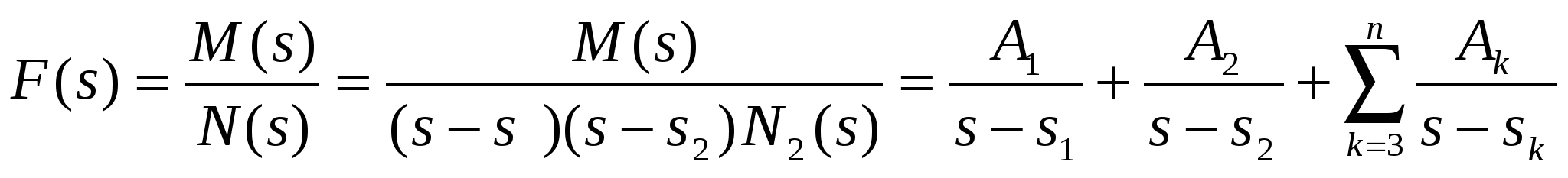
Формула справедлива и для комплексных чисел.
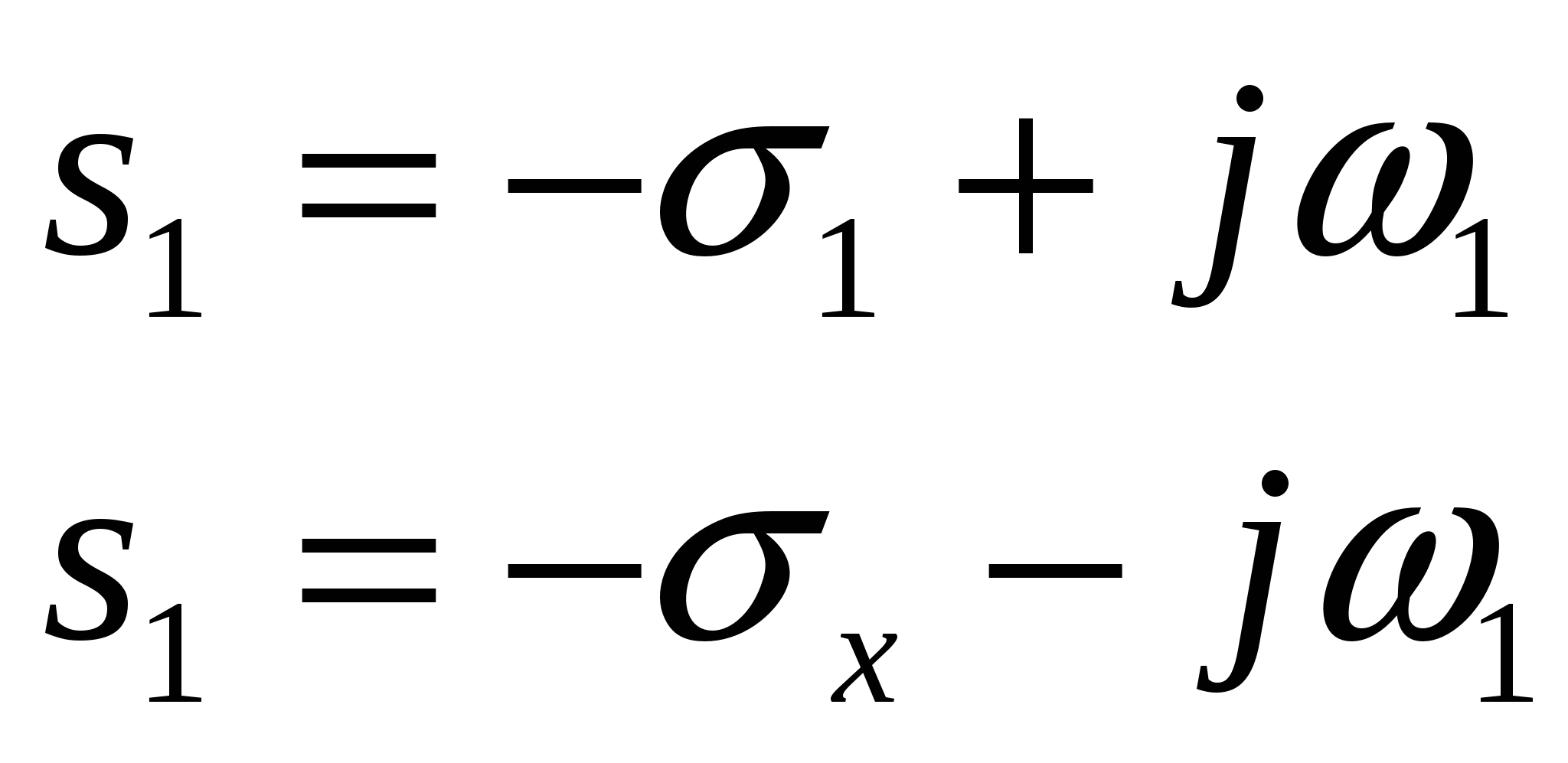 Коэфиценты Ai – комплексные Коэфиценты Ai – комплексные
А2=А1
Воспользуемся формулой (3)
 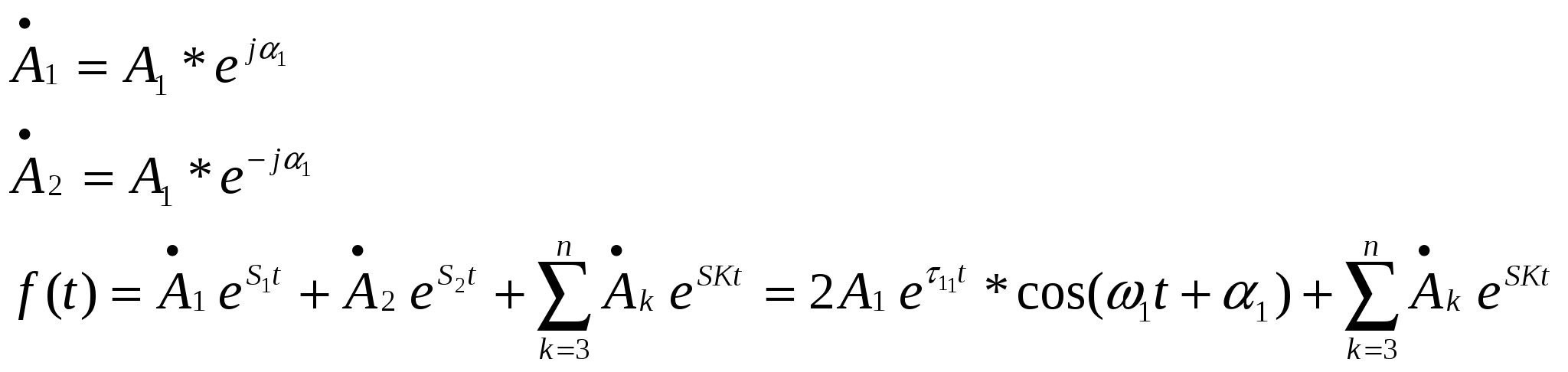
В случае наличия двух комплексных сопряж. полюсов в реакции имеется гарм. Функция, затухающая по е.
|
49. Обратное преобразование Лапласа. Теорема разложения для случаев простых кратных полюсов изображения.
Так как 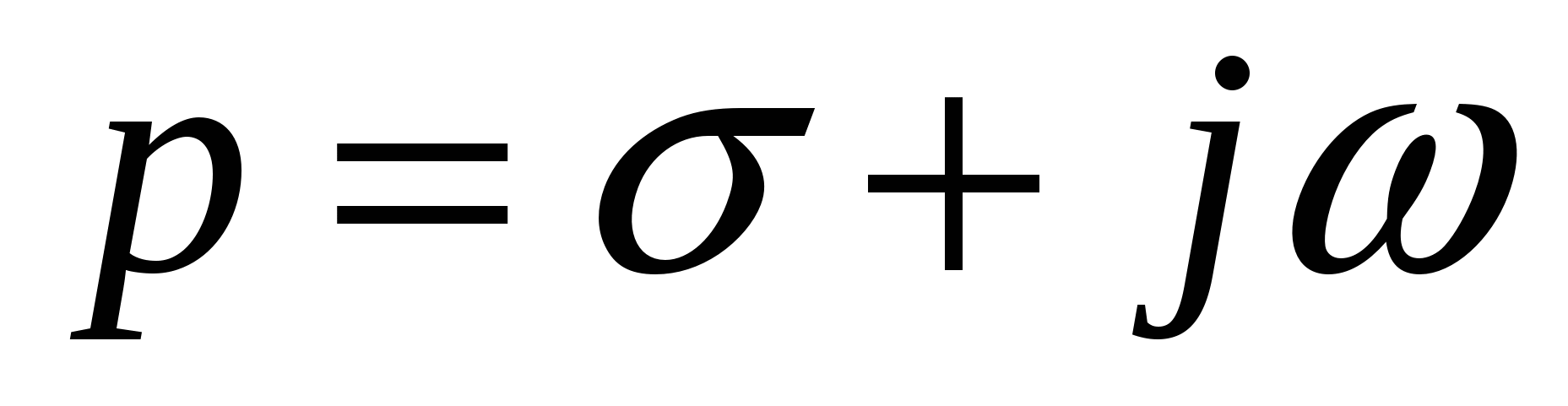 , то , то 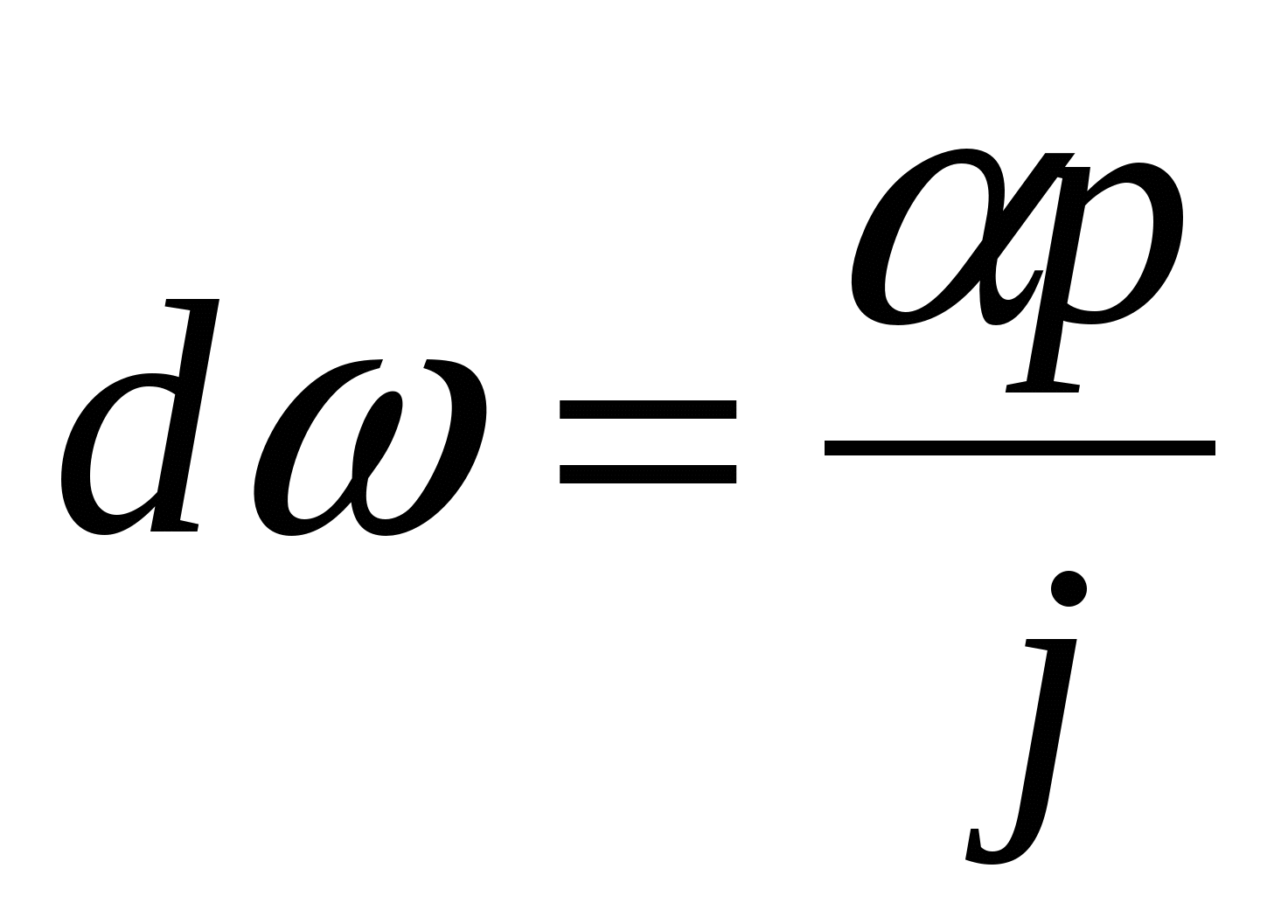 , a пределы интегрирования в при изменении , a пределы интегрирования в при изменении  от от 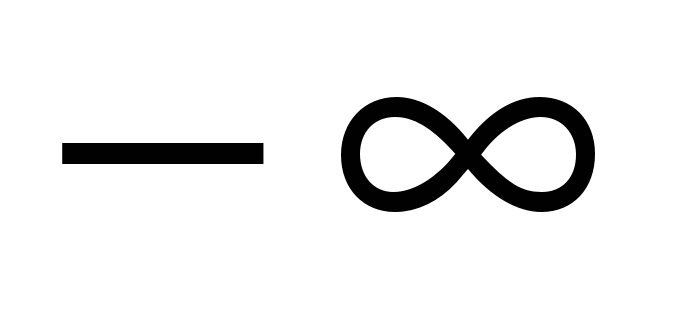 до до 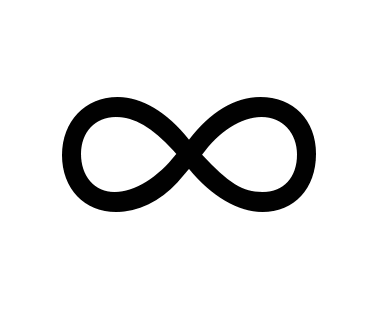 теперь будут соответственно теперь будут соответственно 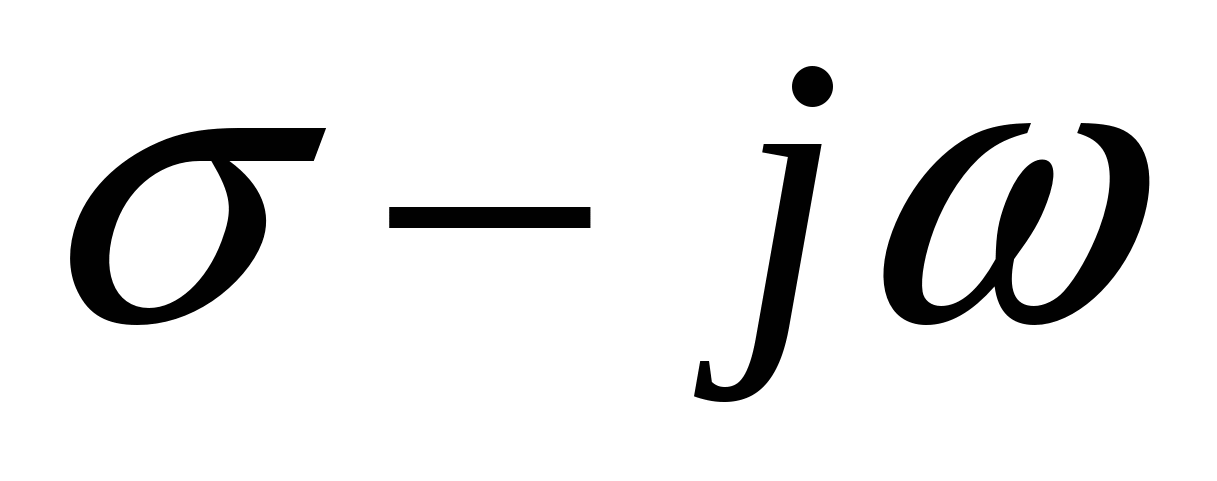 и и 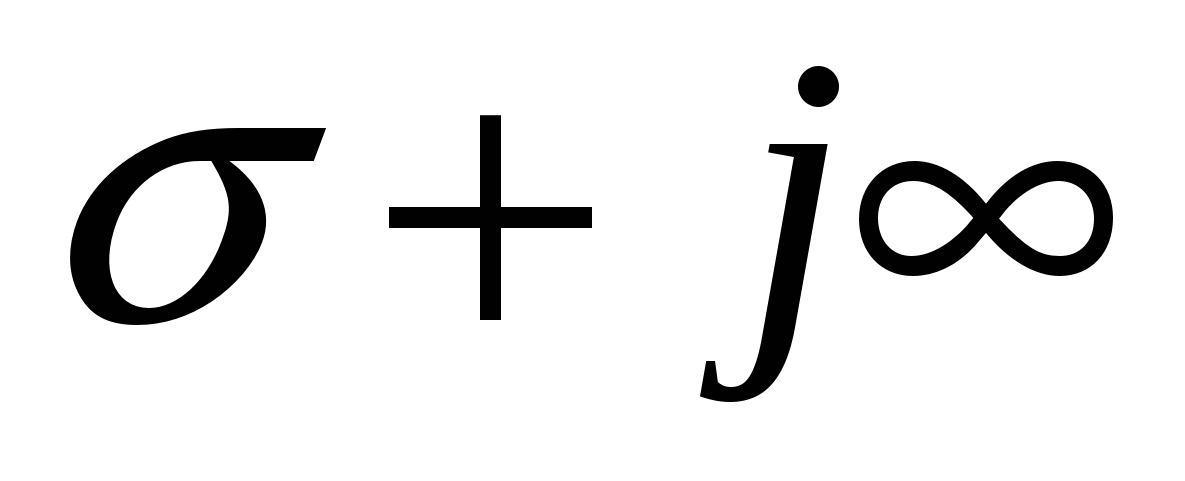 .Тогда получаем: .Тогда получаем:
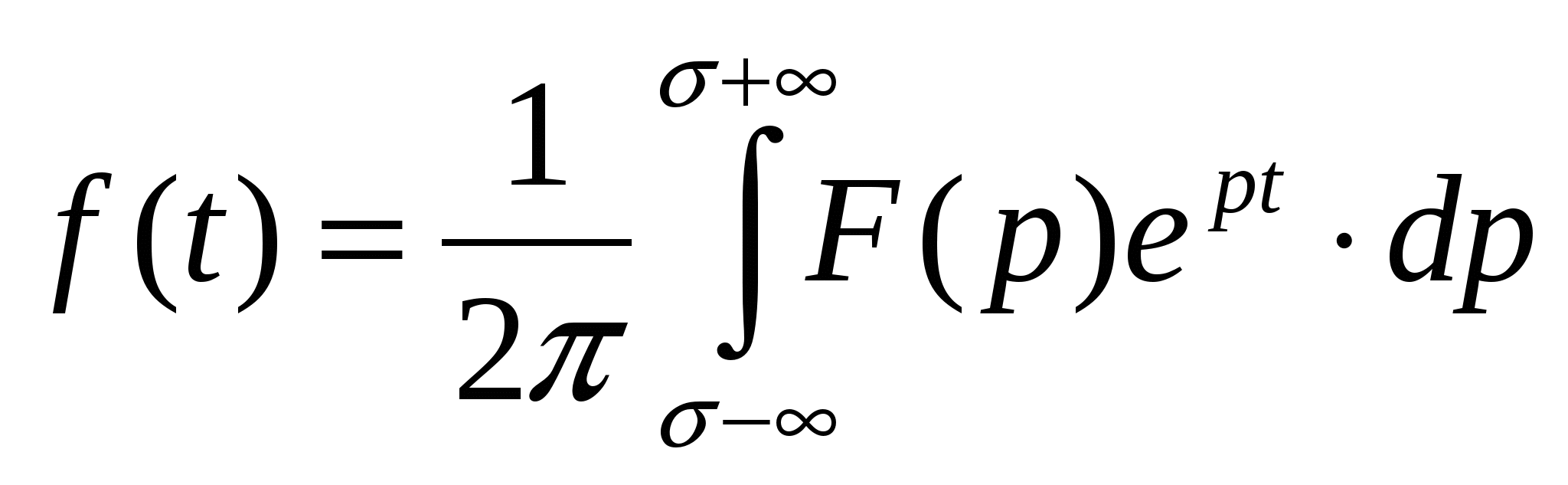 . .
Простая кратная прохерь:
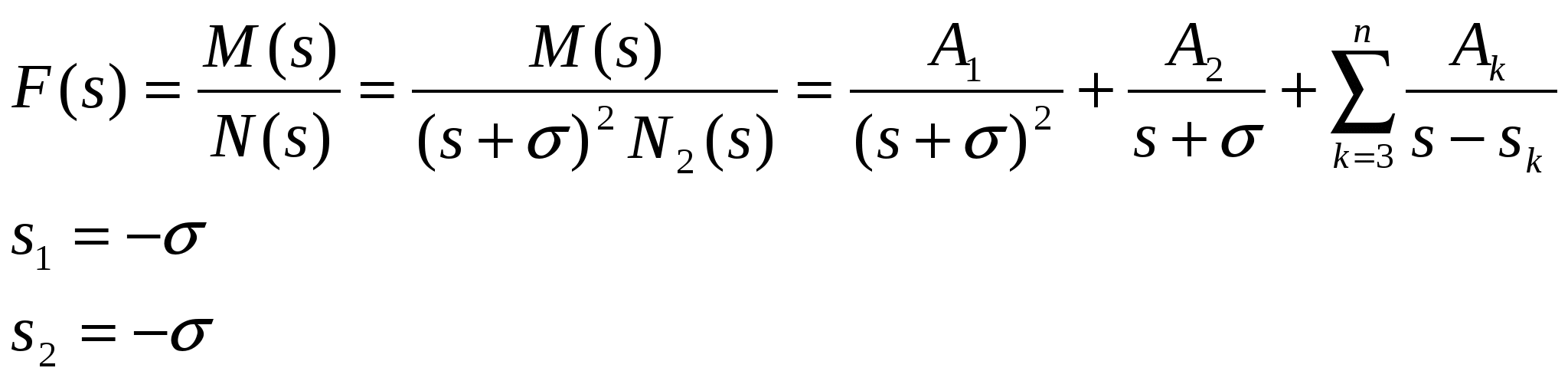
Для нахождения А1 обе части домножим на 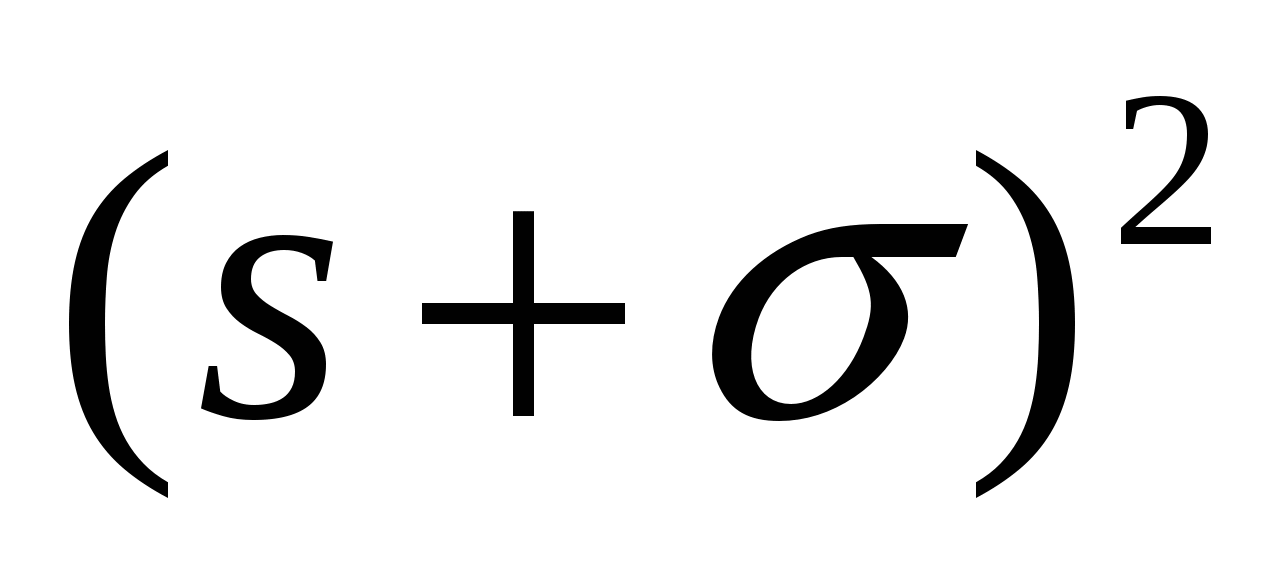 : :
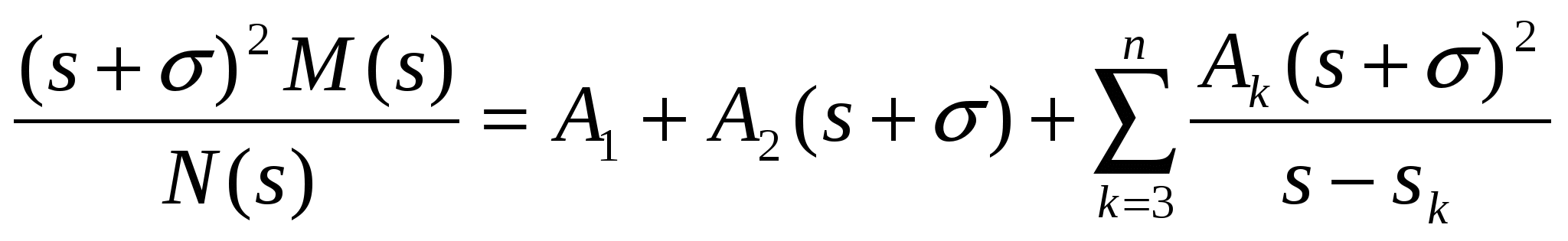 (4) (4)
После подстановки 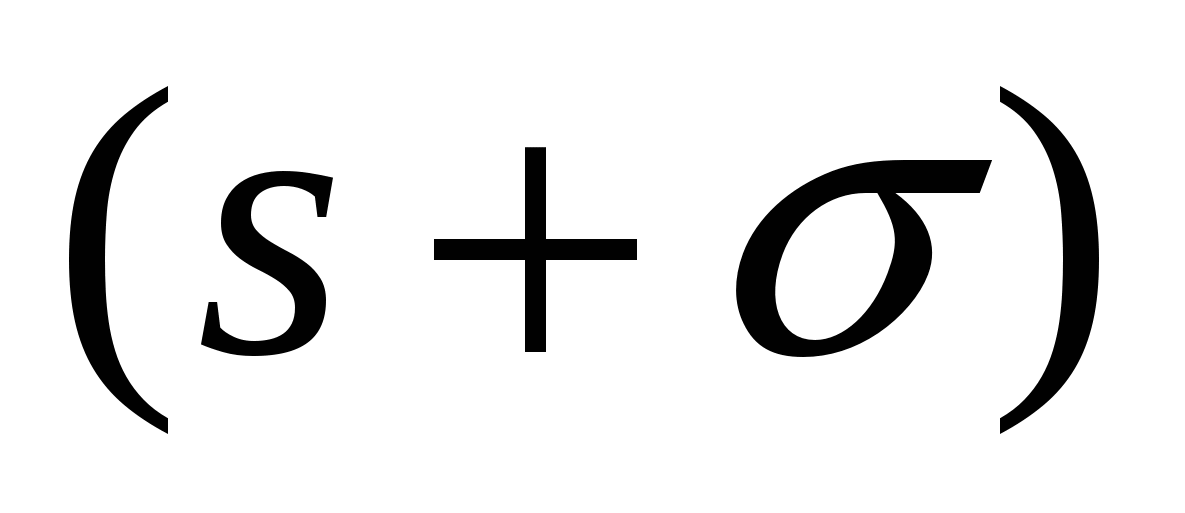 находим: находим:
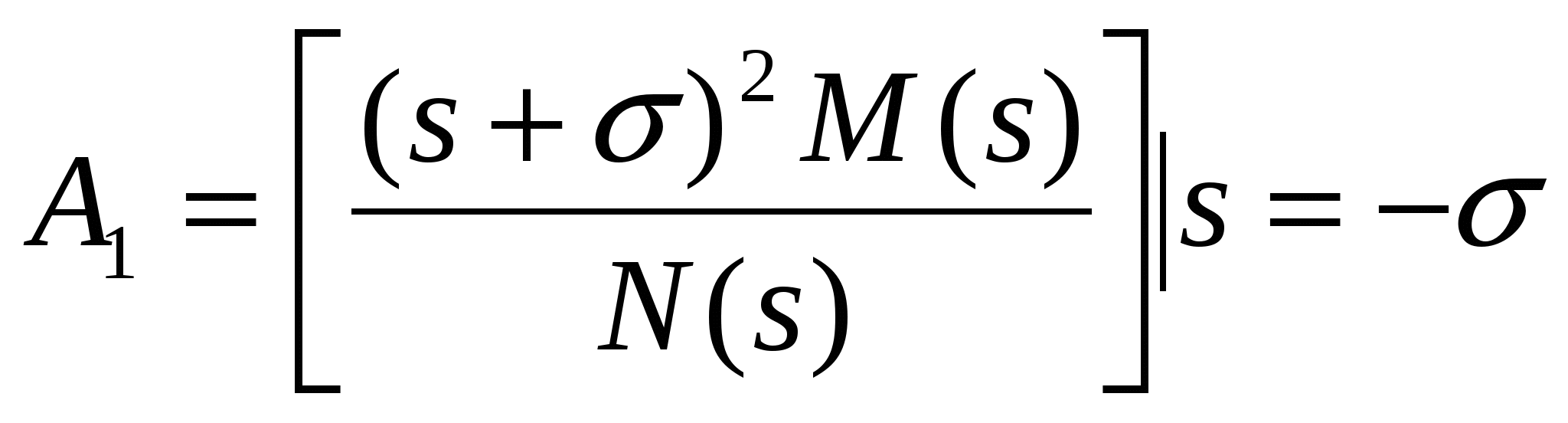
Продифференцируем обе части выражения (4) по S:
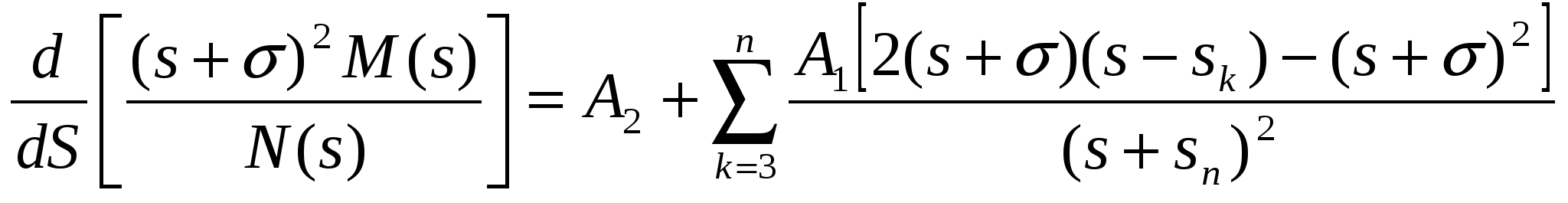
Выполним подстановку 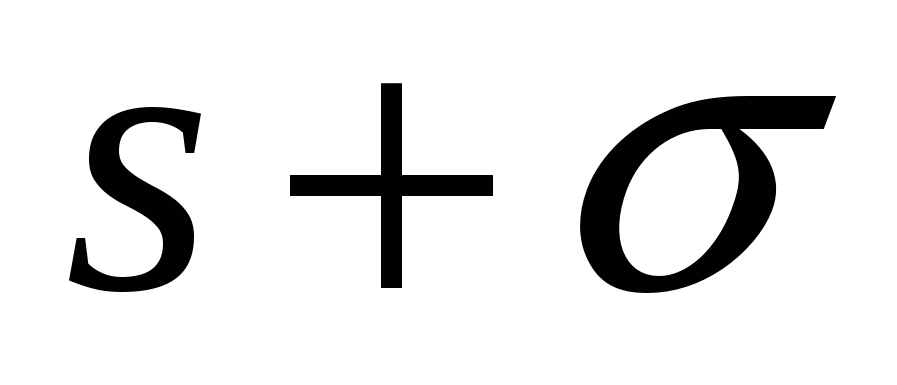 =0 =0
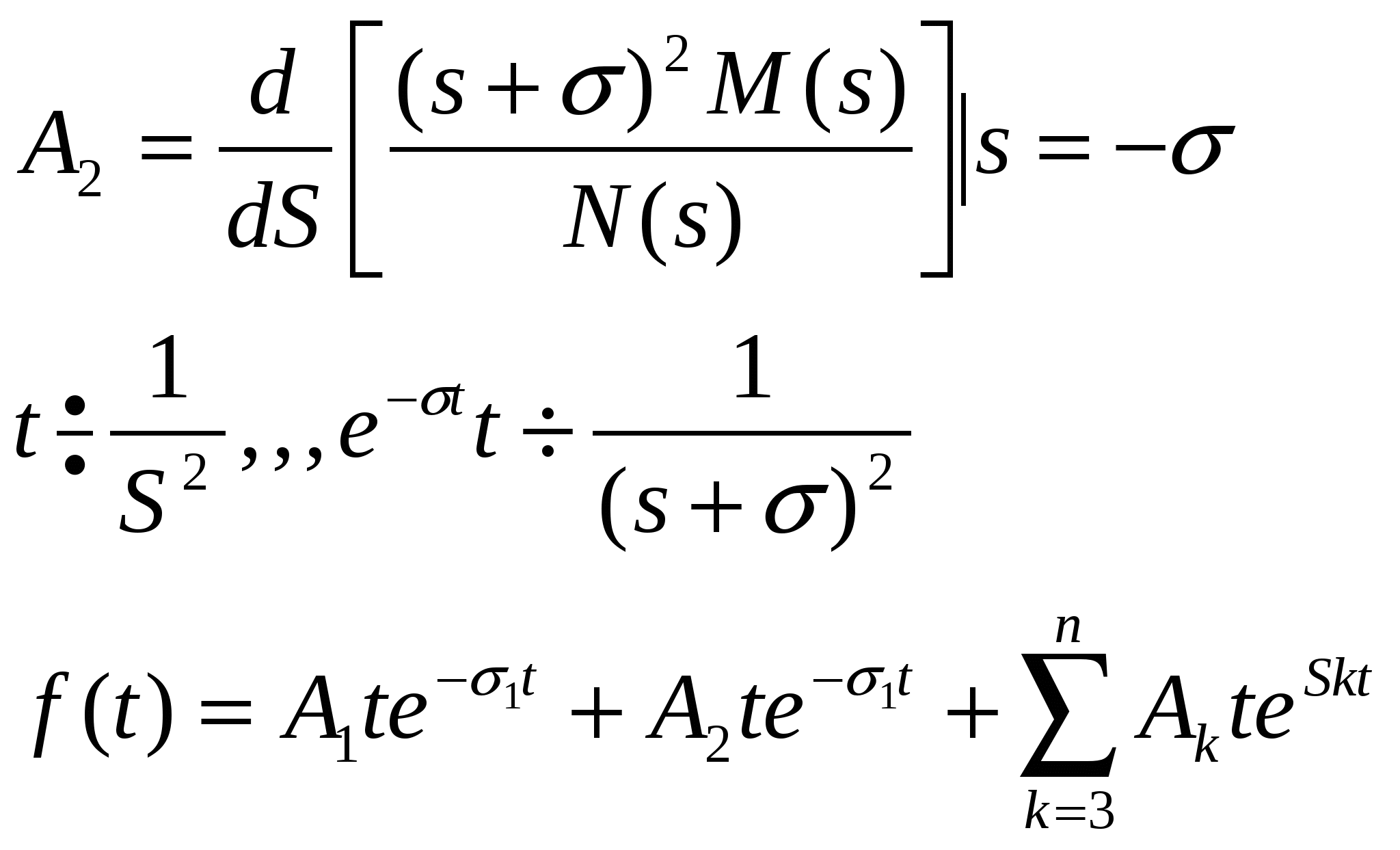
|
50. Операторная передаточная функция цепи и связь ее с изображениями переходной и импульсной характеристик.
|
51. Точный расчет реакции электрической цепи при установившемся периодическом воздействии.
|
52. Тригонометрическая и косинусная формы записи разложения периоди- ческих сигналов в ряд Фурье. Связь между коэффициентами этих рядов.
Тригонометрическая форма: 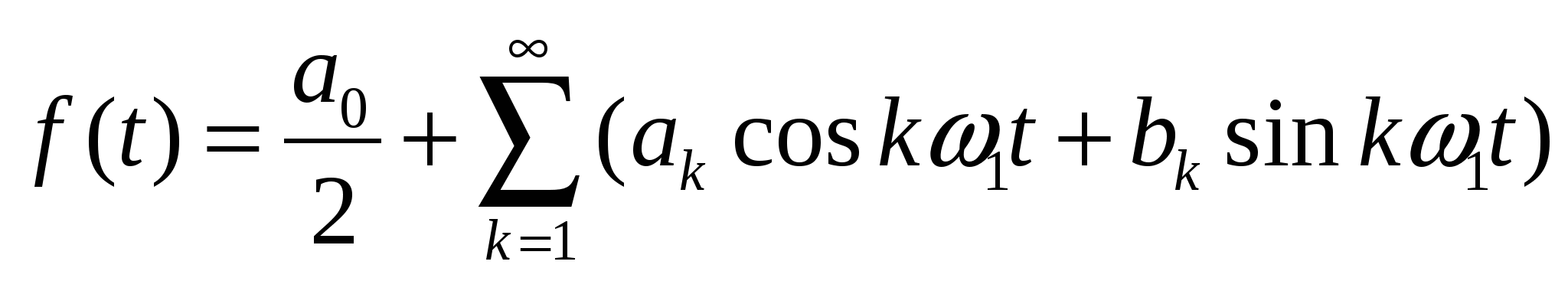 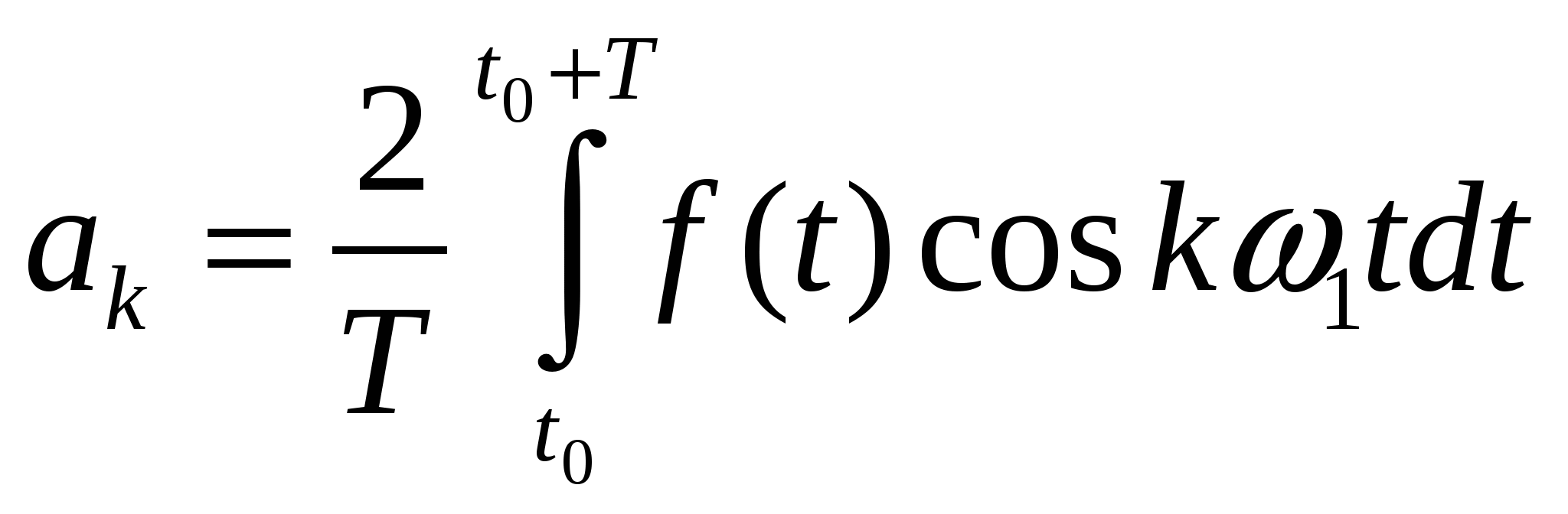
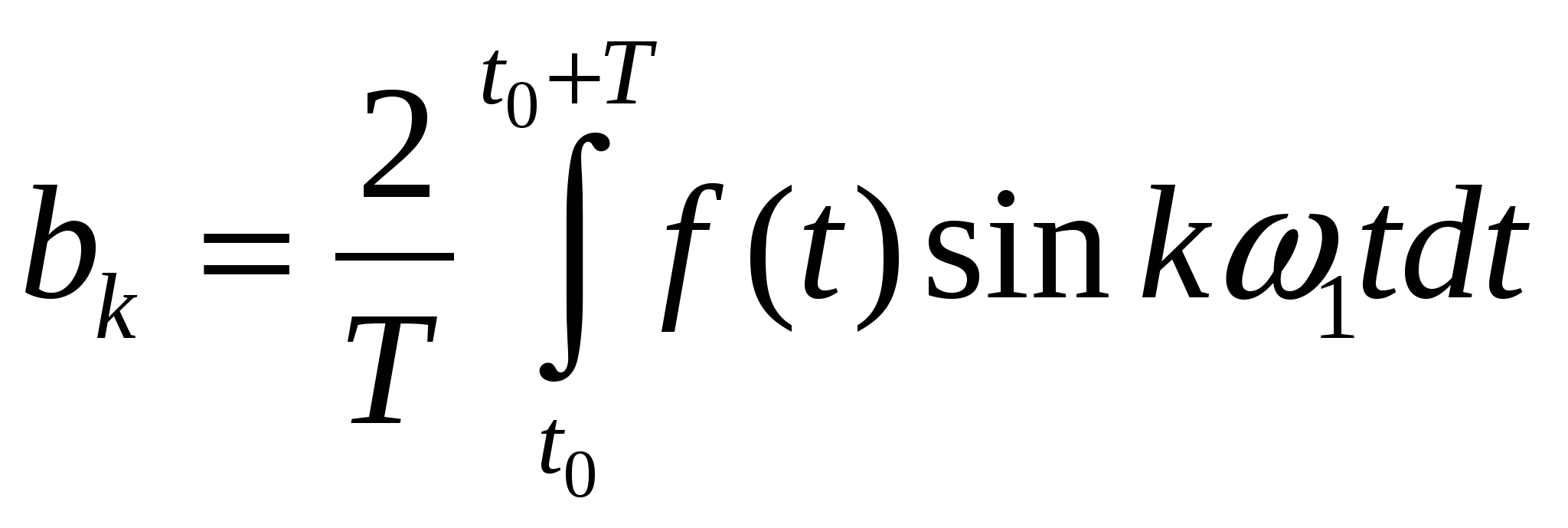 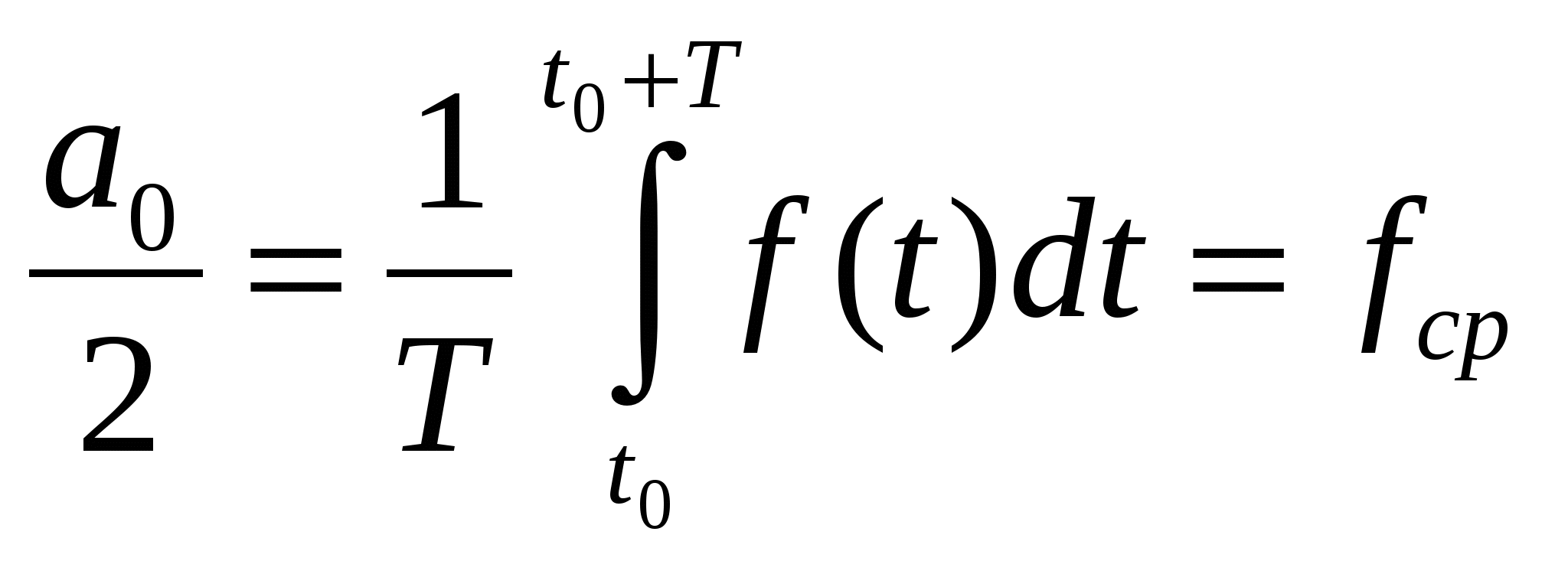 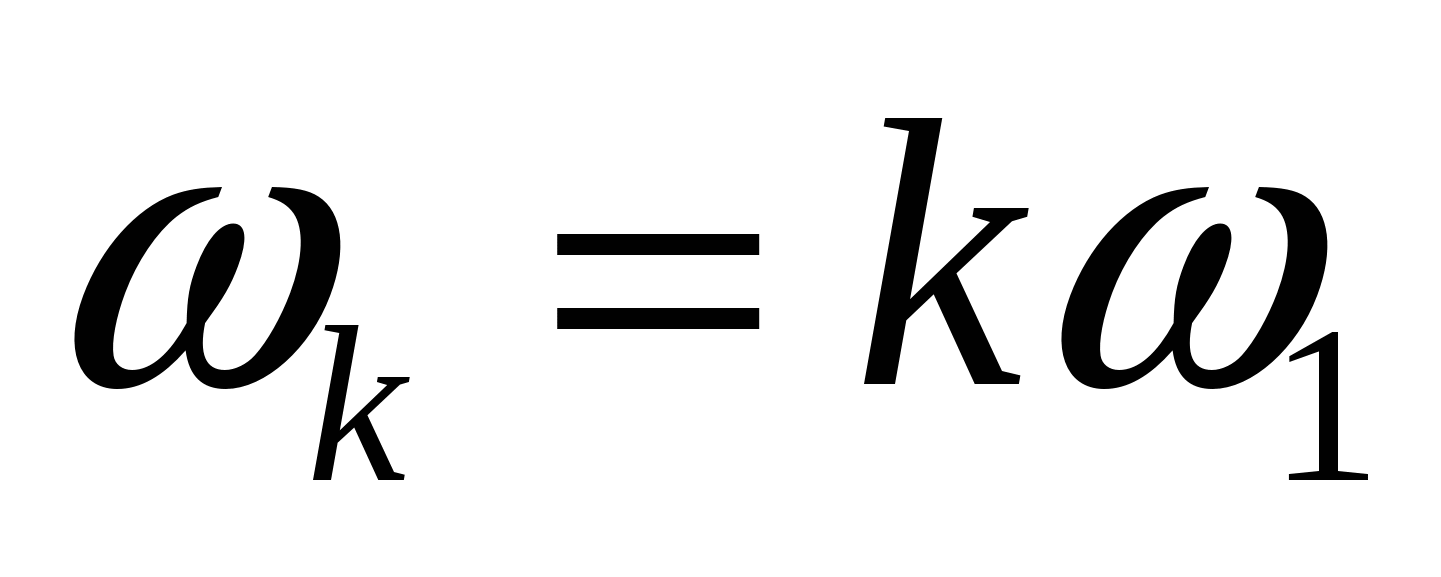
Косинусная форма:
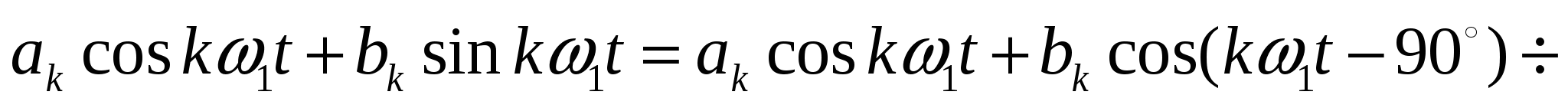
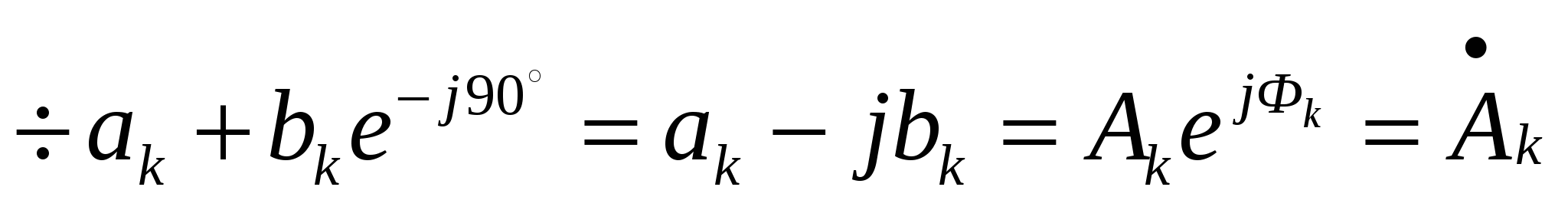
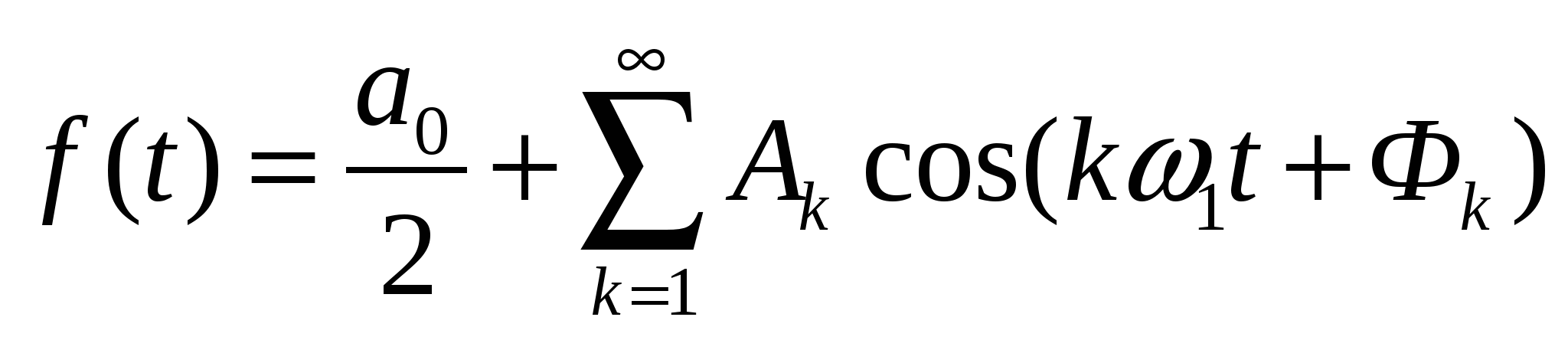 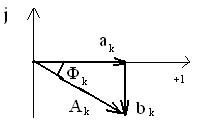
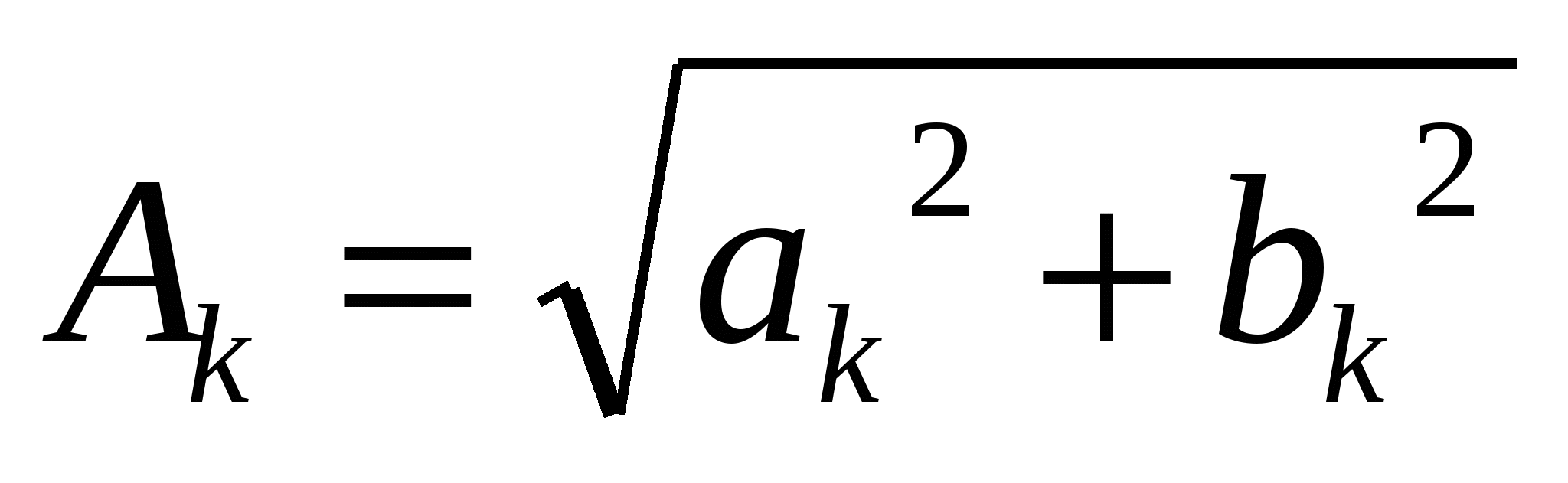 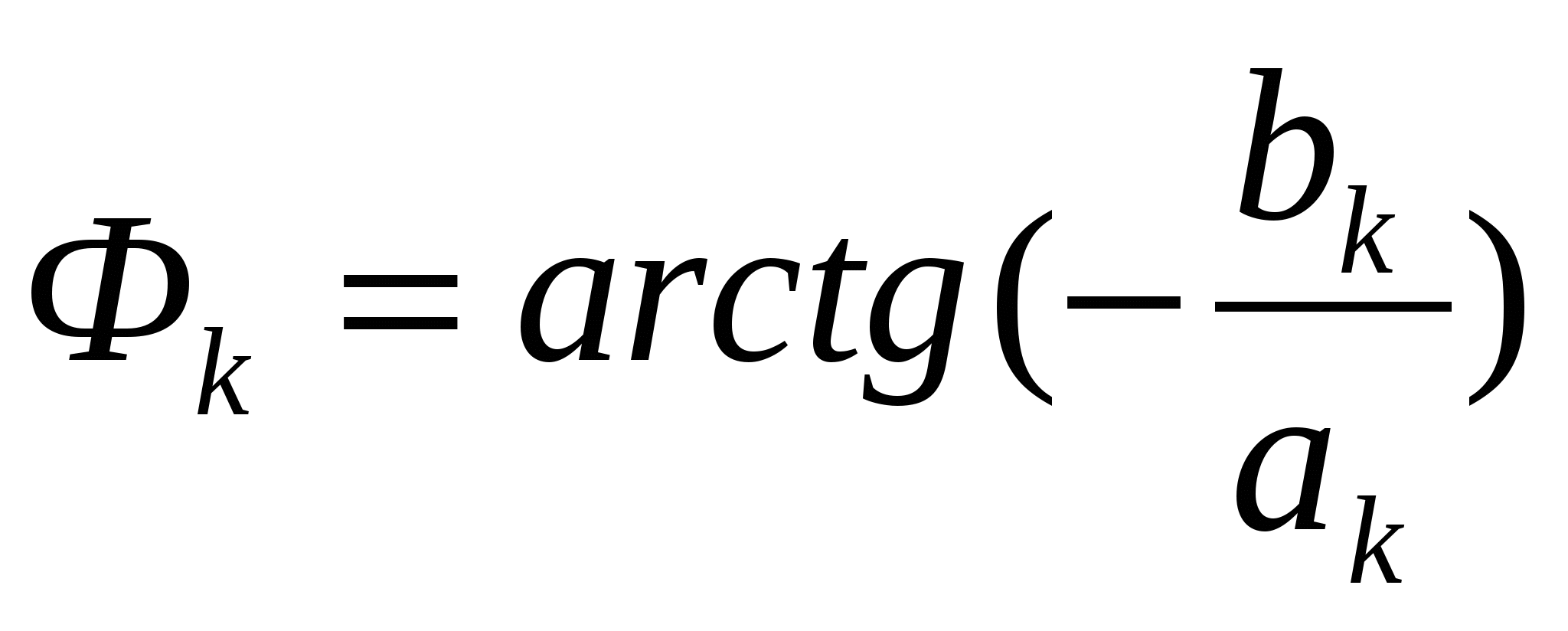
|
53. Расчет активной мощности электрической цепи в установившемся несинусоидальном режиме.
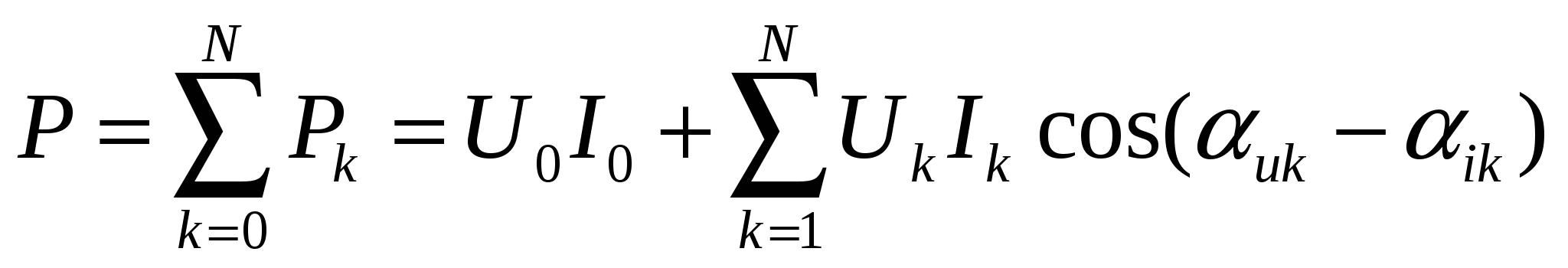
где 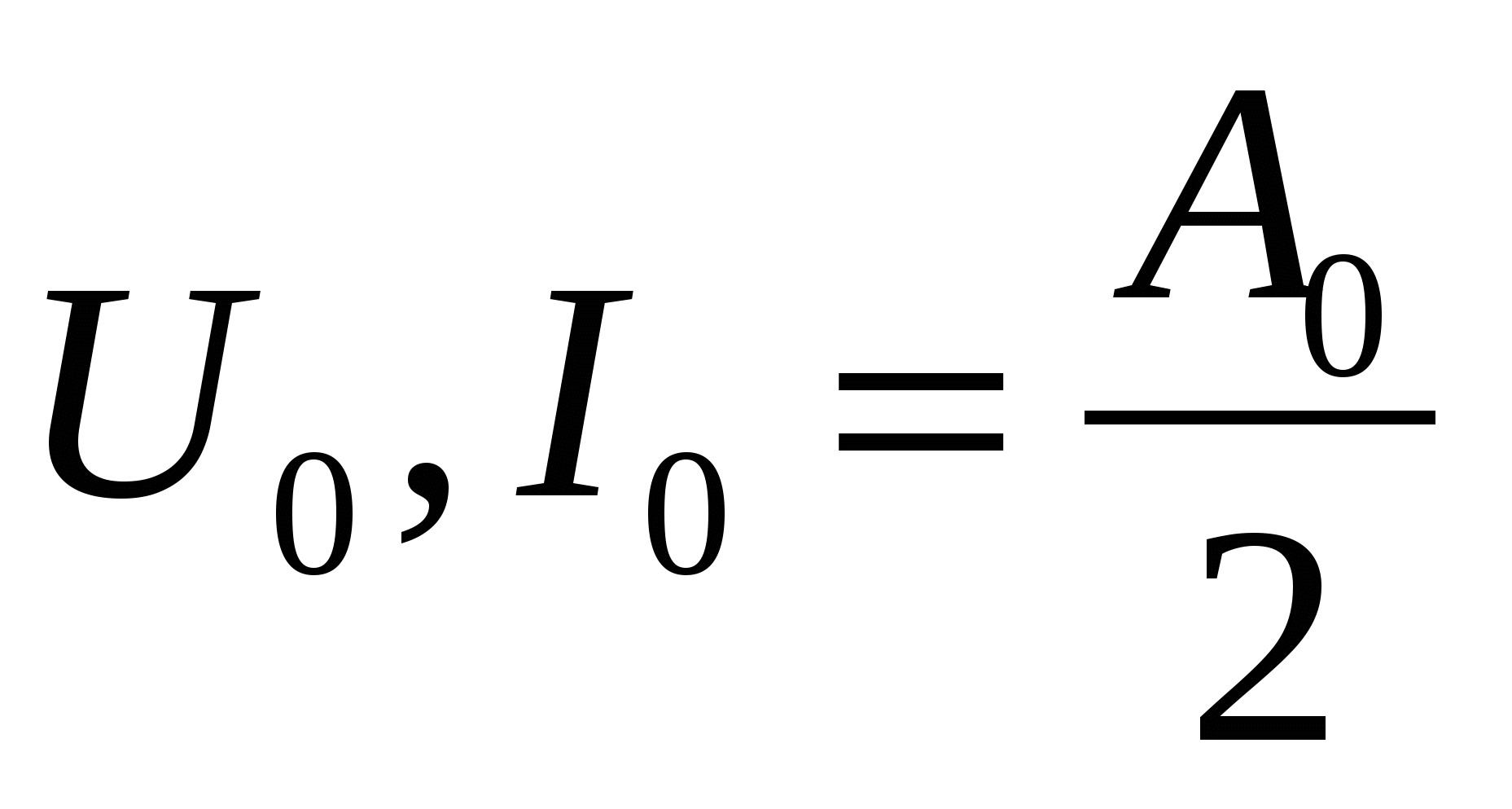 - значения нулевых гармоник - значения нулевых гармоник
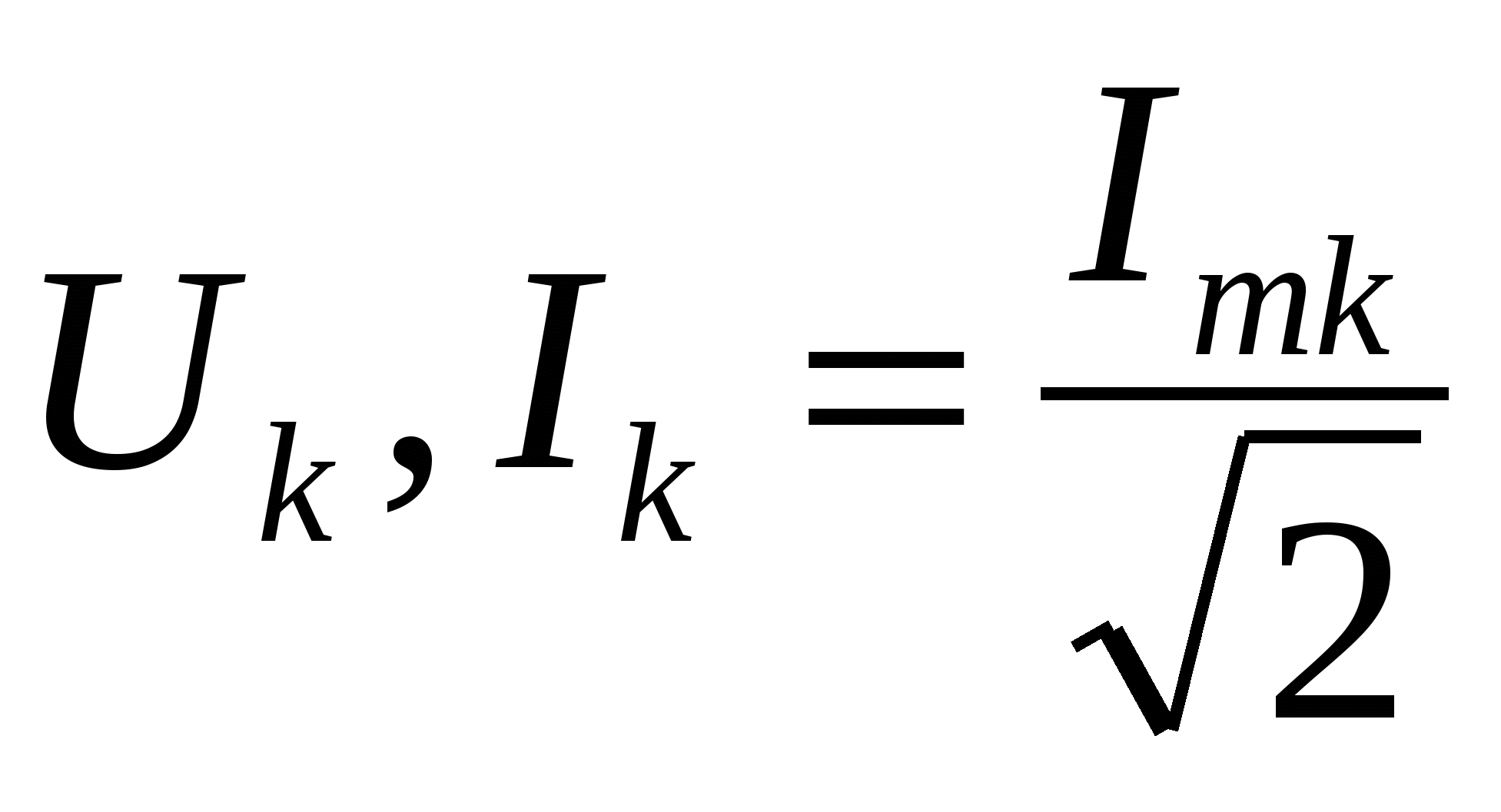 - действующие значения, отдельных гармоник (с амплитудой Ak) - действующие значения, отдельных гармоник (с амплитудой Ak)
|
54. Действующее значение периодических несинусоидальных токов и напряжений.
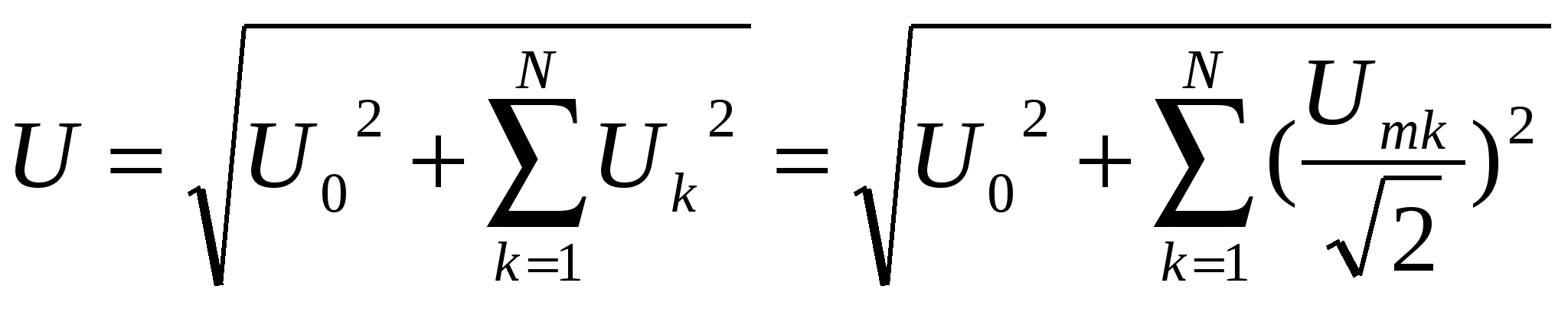
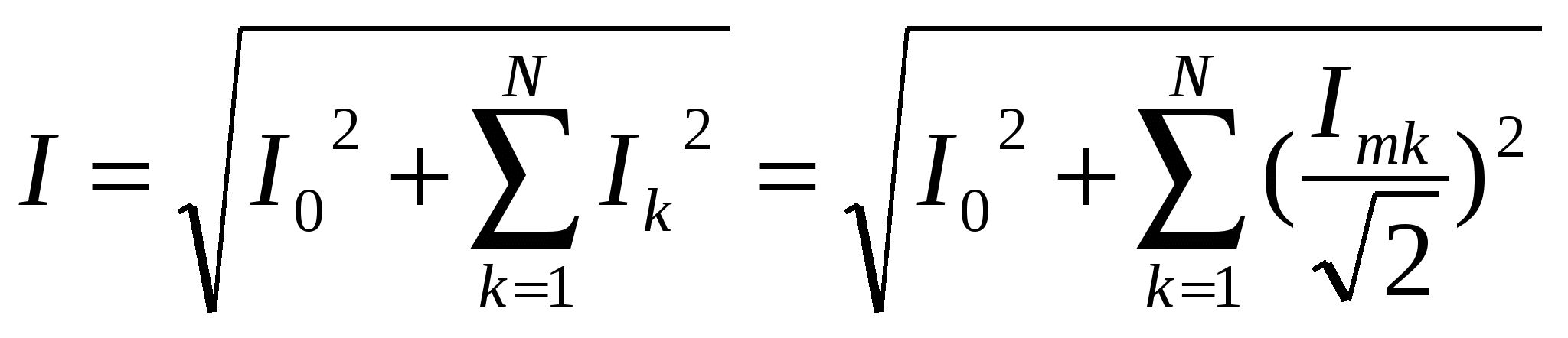
где 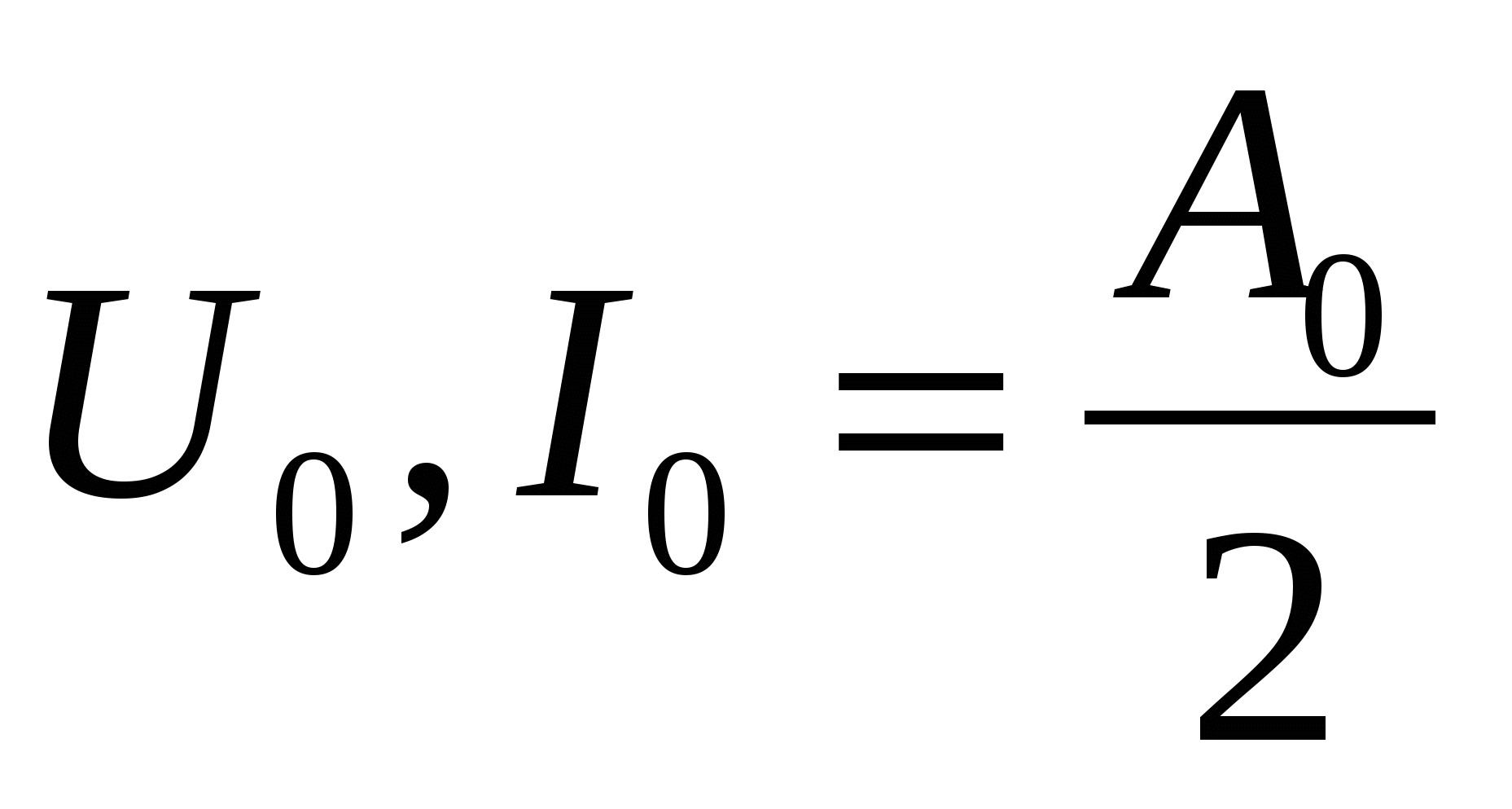 - значения нулевых гармоник - значения нулевых гармоник
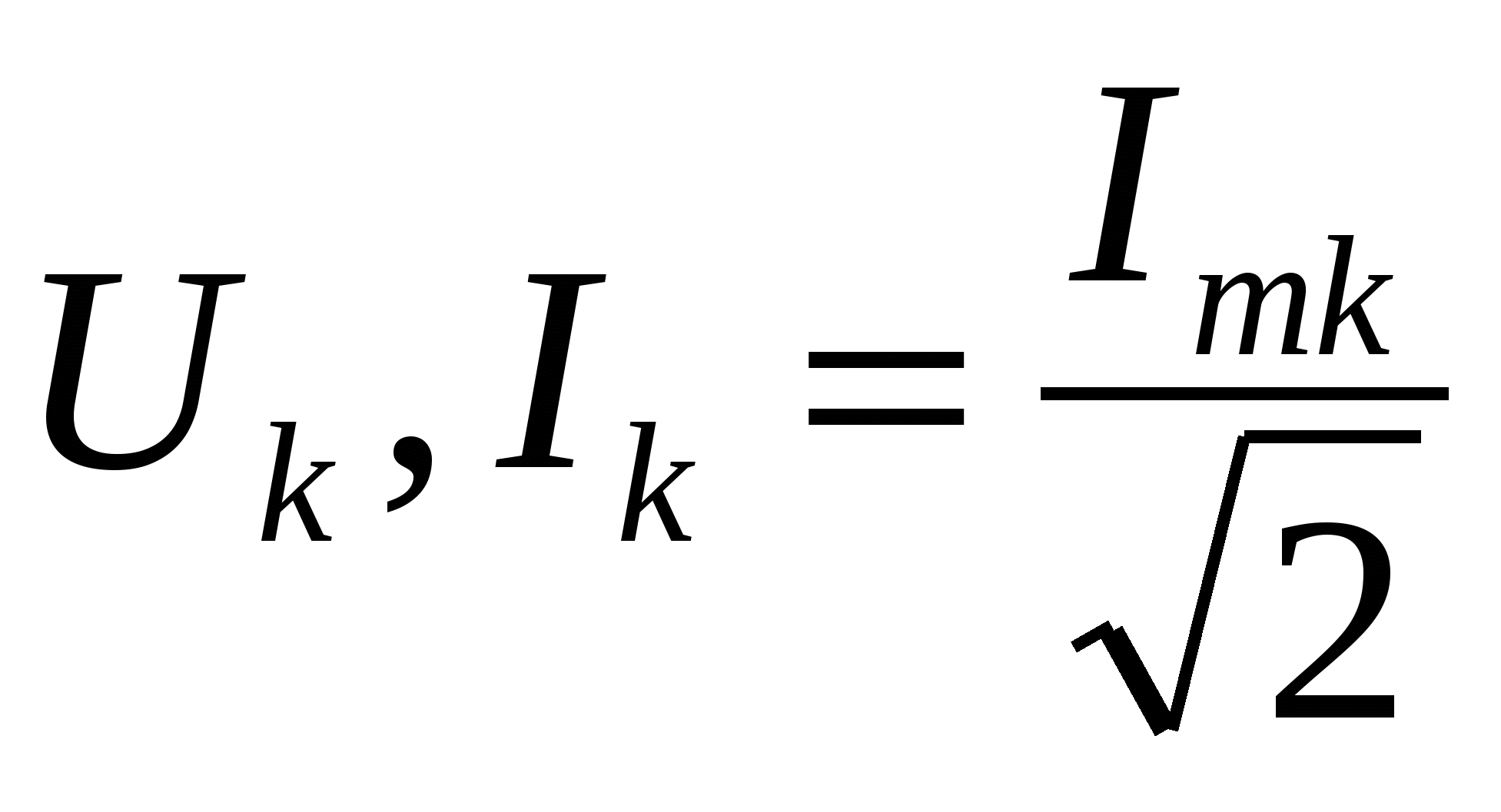 - действующие значения, отдельных гармоник (с амплитудой Ak) - действующие значения, отдельных гармоник (с амплитудой Ak)
|
55. Общая методика расчета установившегося несинусоидального режима электрической цепи.
|
56. Комплексная форма ряда Фурье.
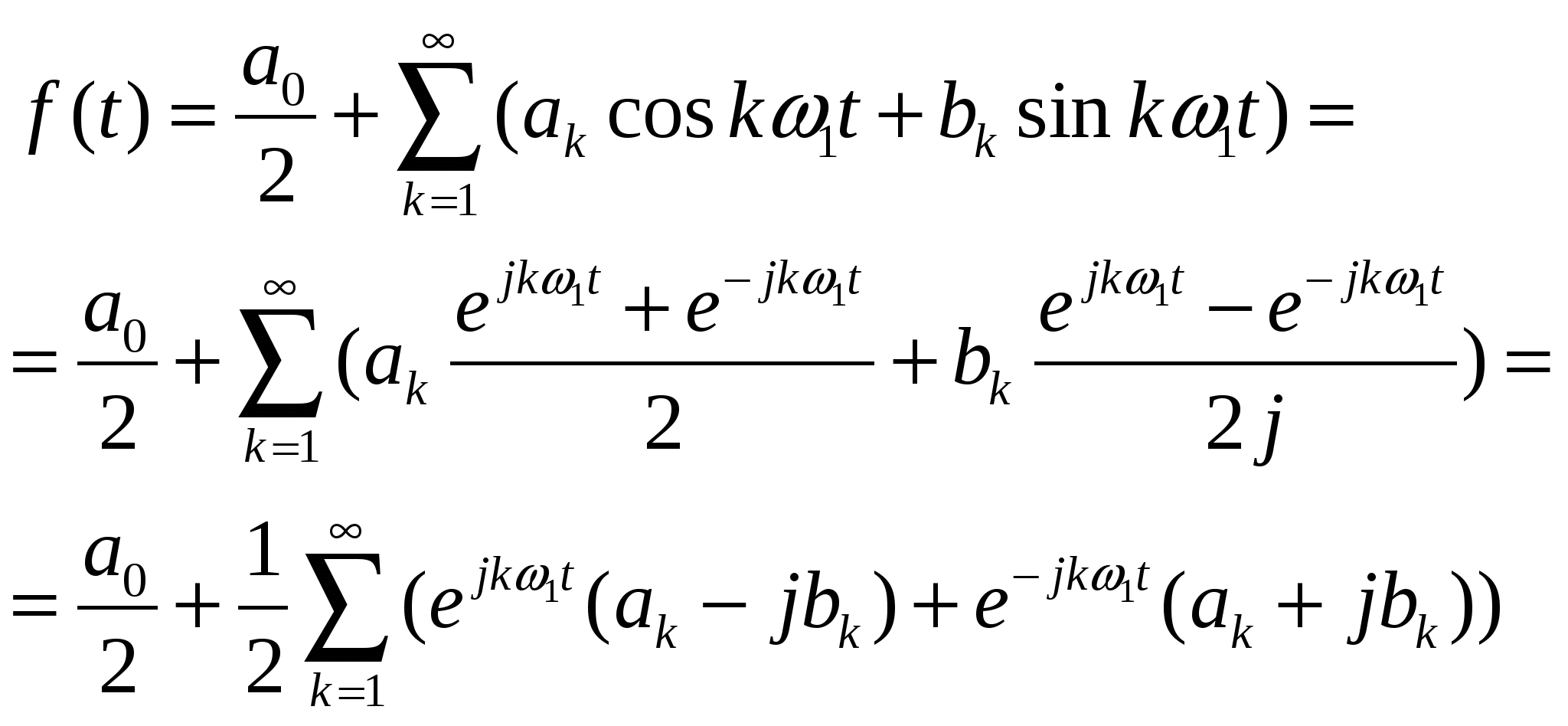 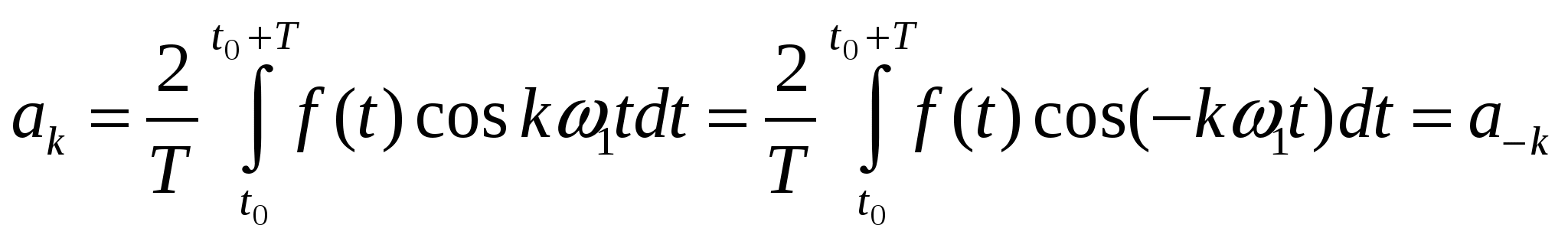 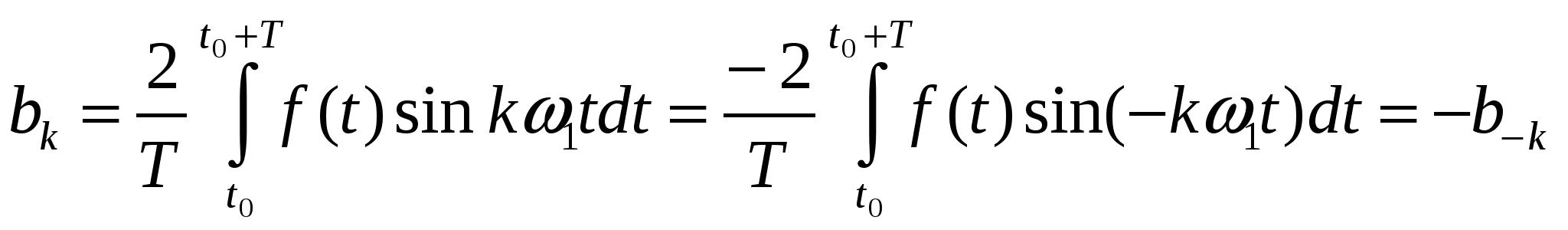 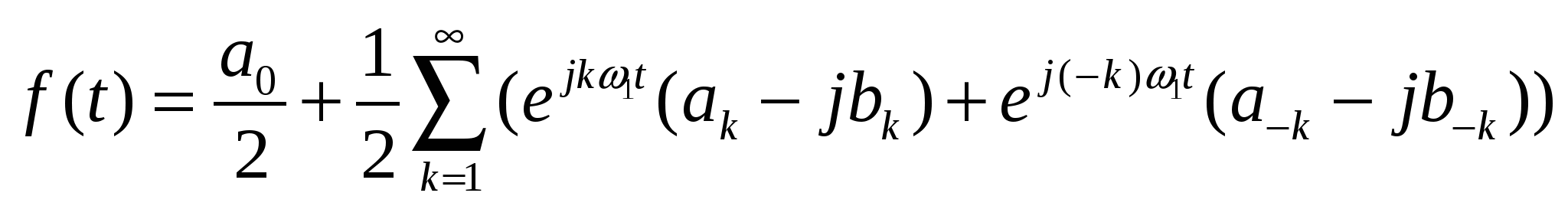 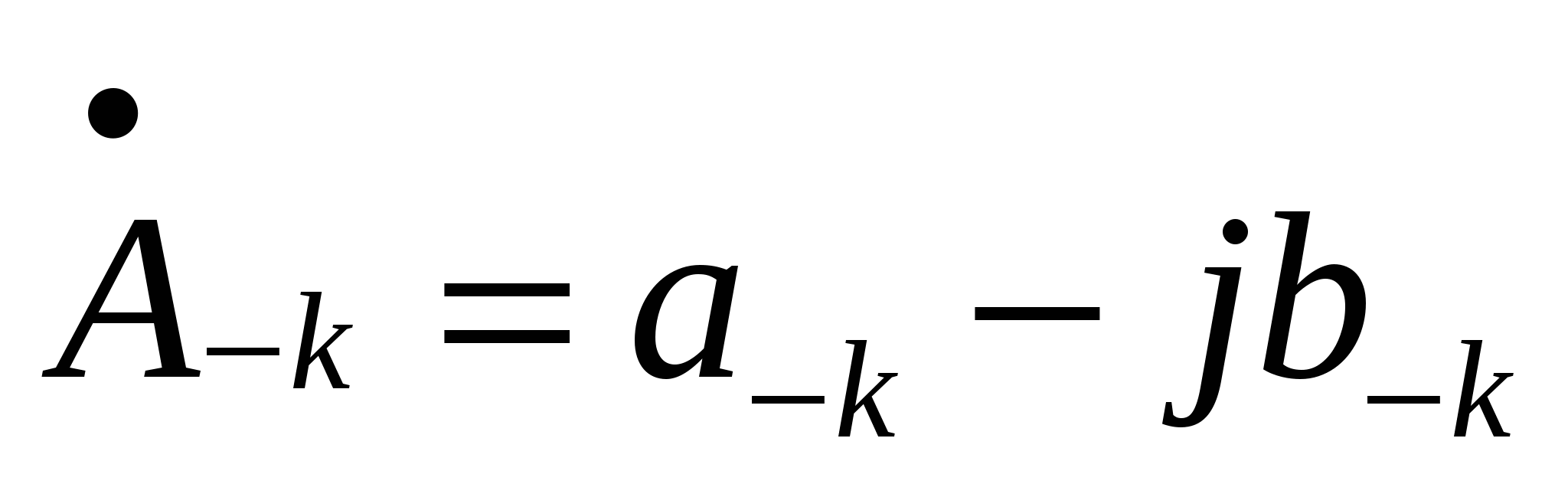
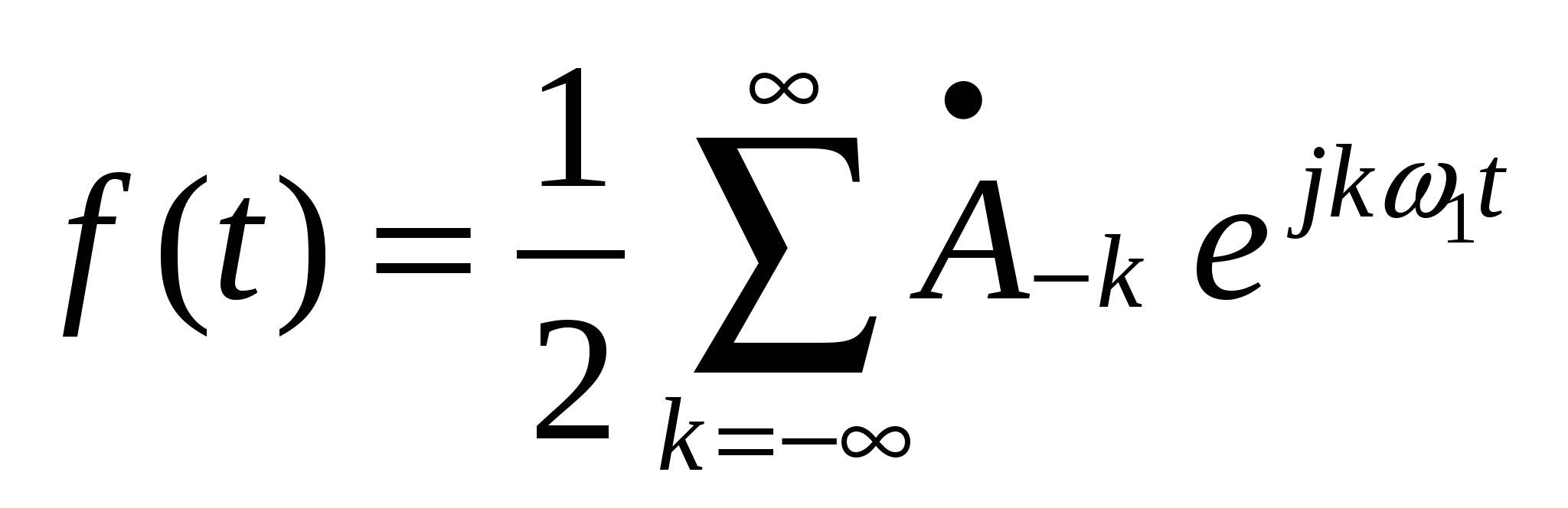
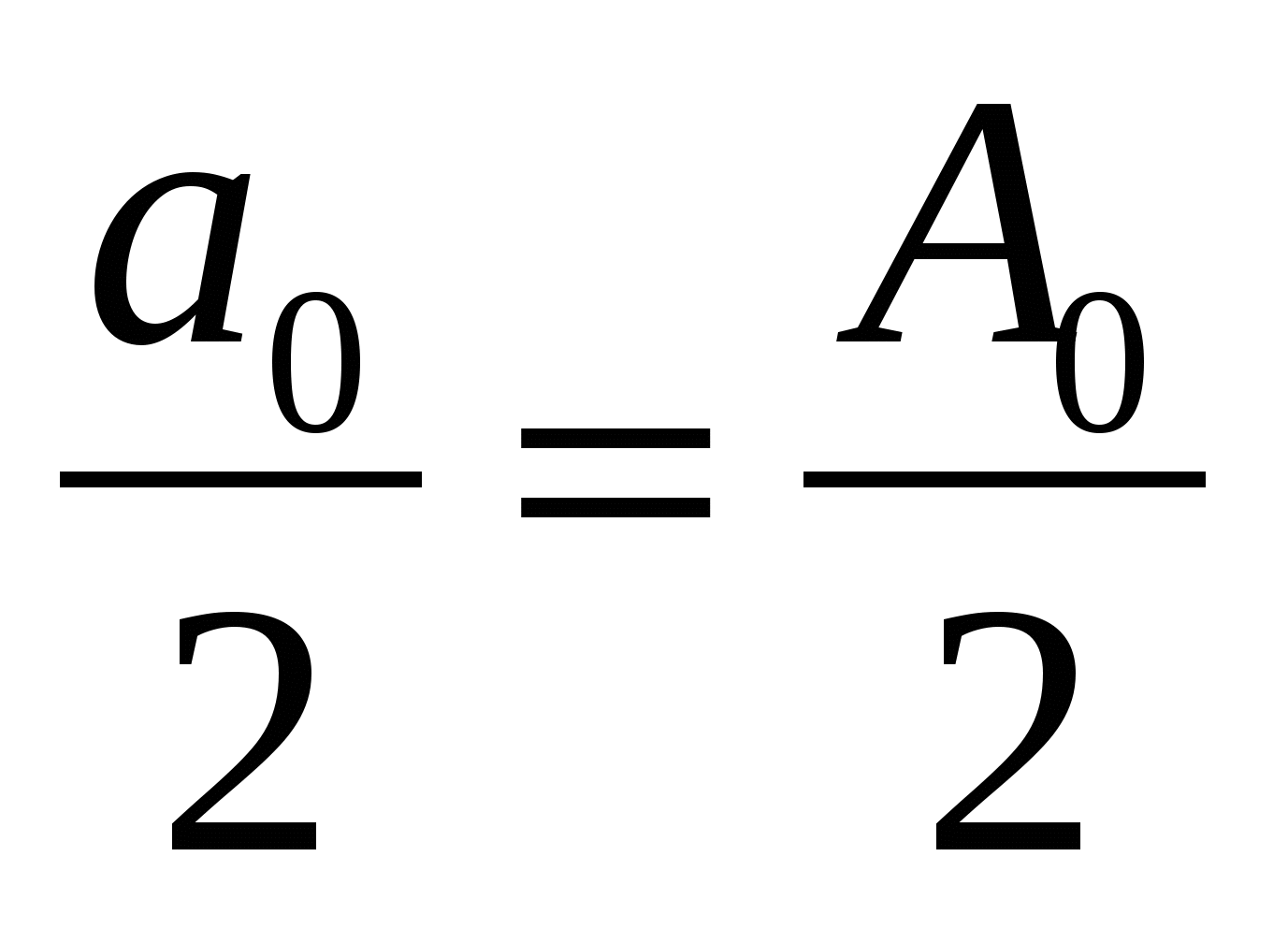 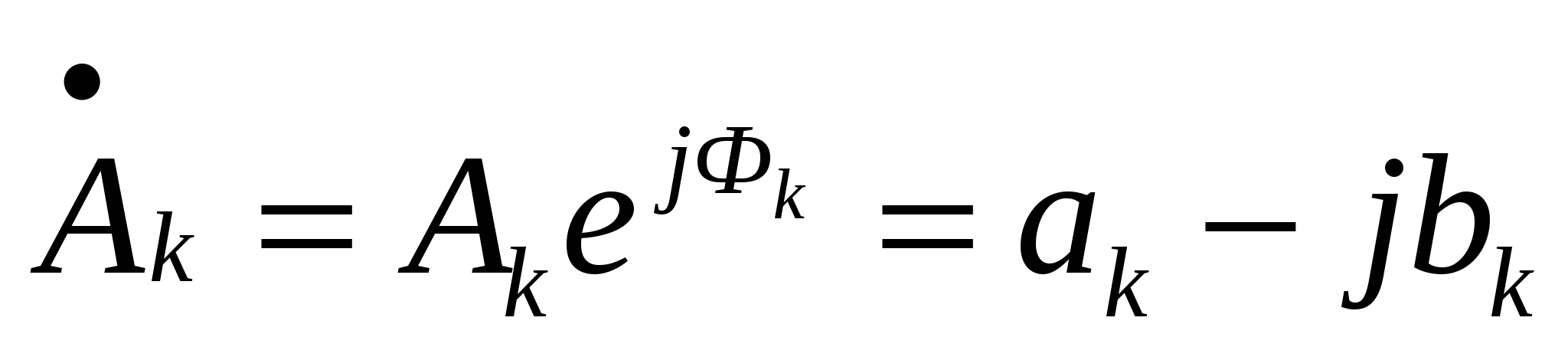
|
57. Понятие о комплексной спектральной характеристике и комплексной амплитуде периодического несинусоидального сигнала.
Спектр сигнала - совокупность синусоидальных составляющих с различными частотами Математической базой для спектрального представления сигналов являются аппарат рядов Фурье для периодических функций и интегралов Фурье — для непериодических. Анализ цепи под действием каждой отдельной синусоидальной составляющей производится с помощью уже изученных методов (например, комплексного метода). Для нахождения временной зависимости искомой величины используют принцип наложения. Описанный подход и составляет частотный (спектральный) метод расчета цепи. Сигнал, обладающий свойством периодичности f(t)=f(t + T ) , удовлетворяющий условиям Дирихле, может быть представлен в виде ряда Фурье:
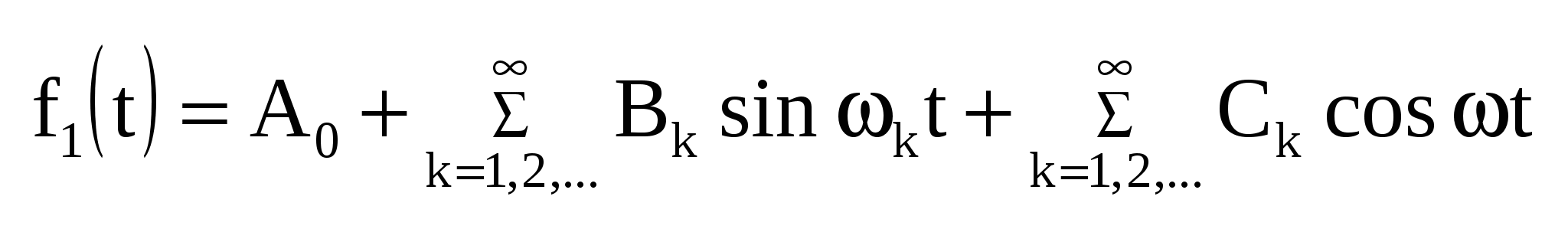 , где , где 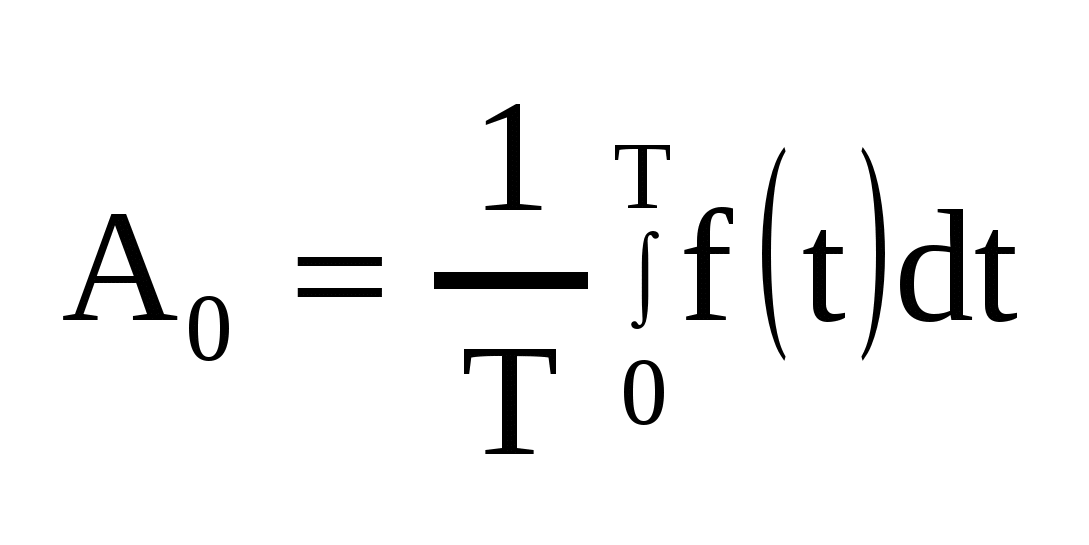 , , 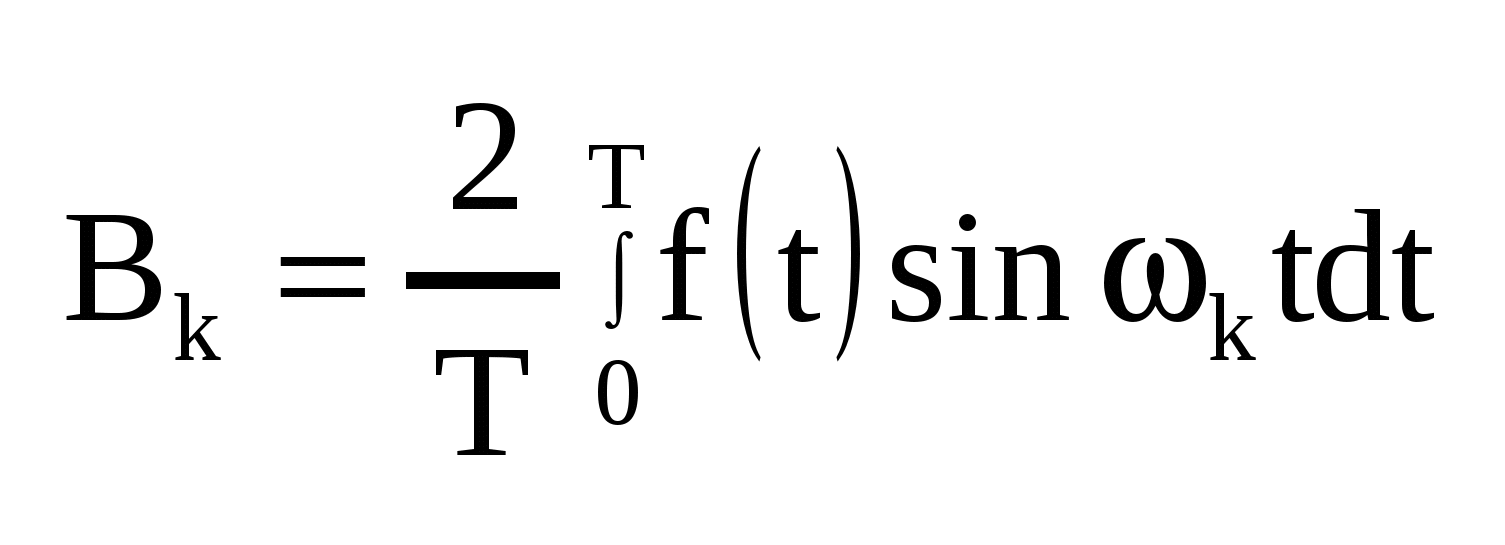 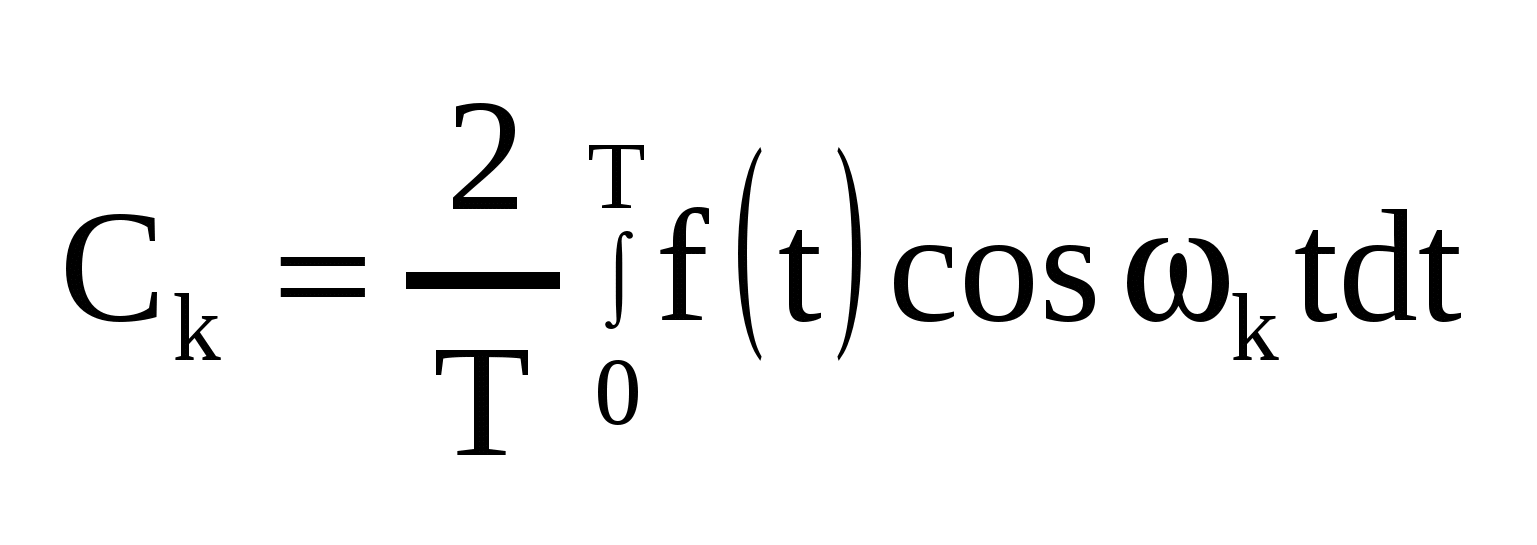 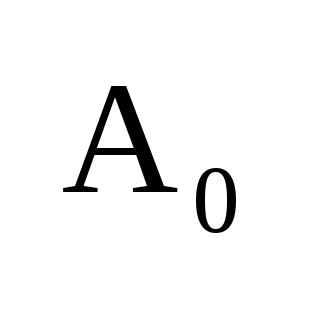 — постоянная составляющая, — постоянная составляющая, 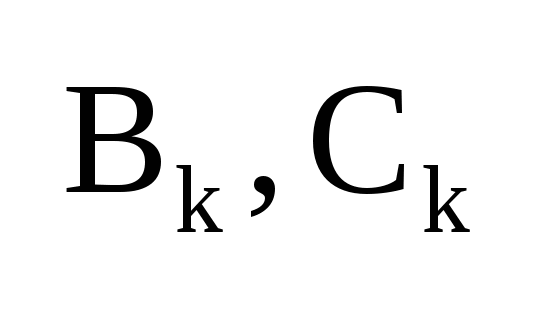 — коэффициенты ряда Фурье, — коэффициенты ряда Фурье, 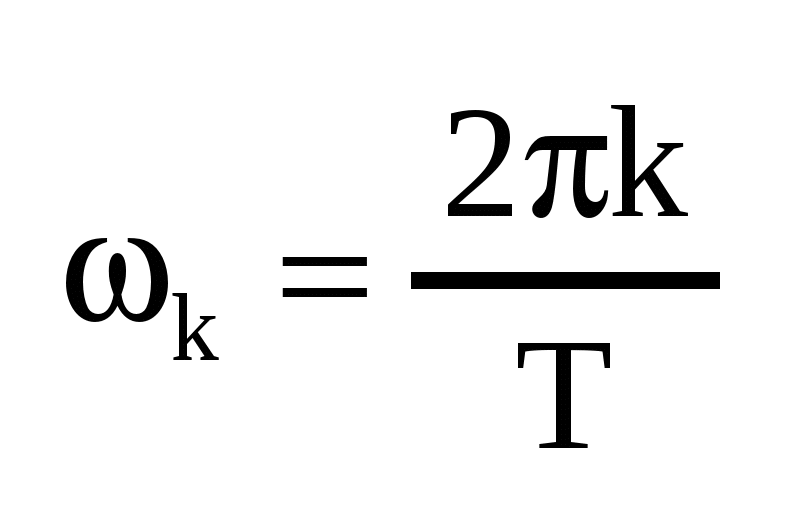 — частоты отдельный синусоидальных составляющих (гармоник), кратные частоте основной(первой) гармоники — частоты отдельный синусоидальных составляющих (гармоник), кратные частоте основной(первой) гармоники 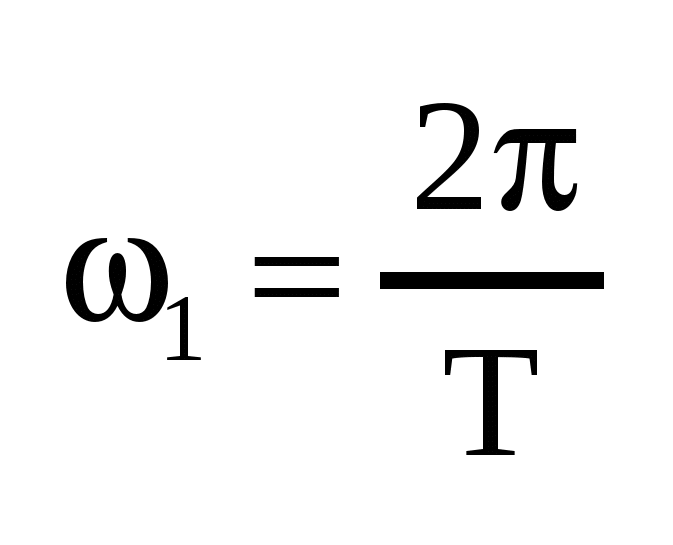 , период которой совпадает с периодом исходного сигнала. , период которой совпадает с периодом исходного сигнала.
Записанное f(t) определяет тригонометрическую форму ряда Фурье. Наиболее компактной и удобной для расчетов формой записи является экспоненциальная (комплексная) форма ряда Фурье.
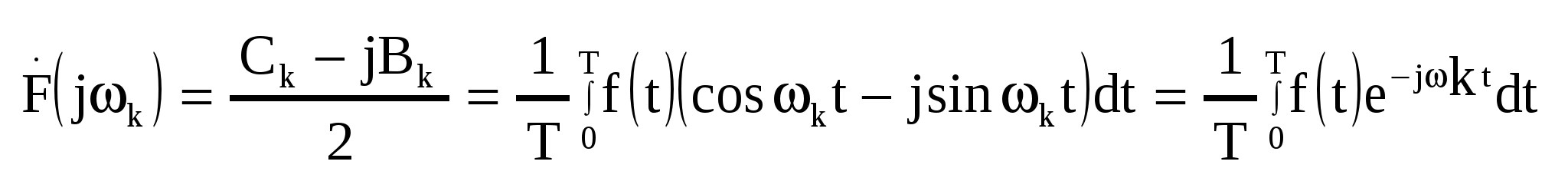
Комплексные коэффициенты позволяют непосредственно выразить амплитуды гармоник и их начальные фазы 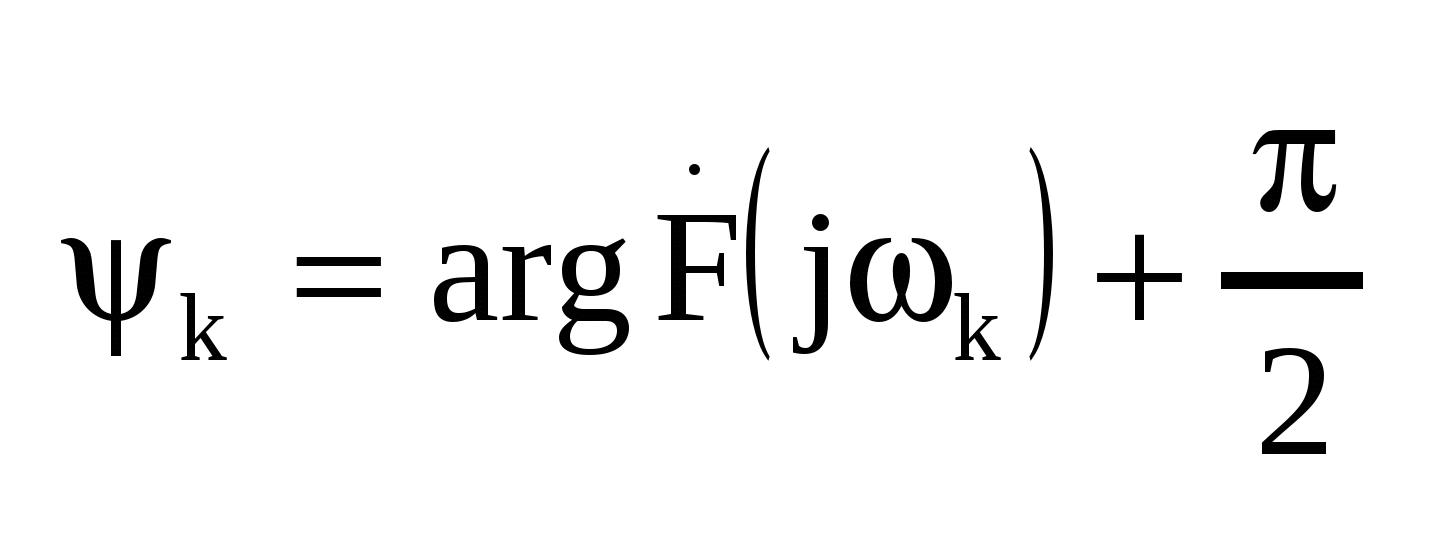 Комплексная амплитуда k-й гармоники выражается следующим образом Комплексная амплитуда k-й гармоники выражается следующим образом 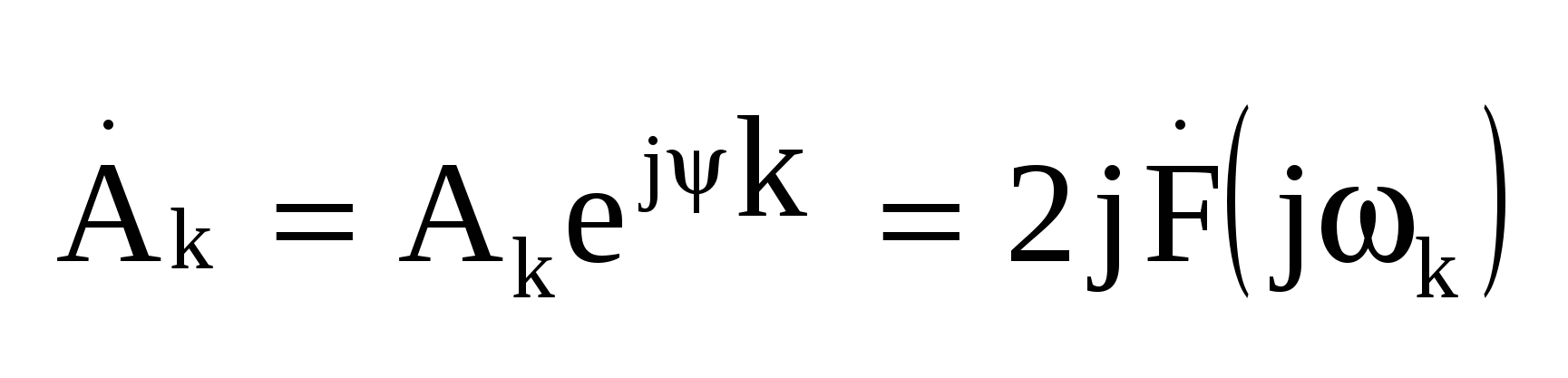 Комплексные коэффициенты с положительными и отрицательными индексами являются комплексно сопряженными. Совокупность комплексных коэффициентов рассматриваемой функции образует ее спектр Комплексные коэффициенты с положительными и отрицательными индексами являются комплексно сопряженными. Совокупность комплексных коэффициентов рассматриваемой функции образует ее спектр
|
58. Спектры непериодических сигналов и их преобразование по Фурье. Интеграл Фурье.
Переход от спектрального представления периодического сигнала к непериодическому можно осуществить, выполняя в полученных соотношениях комплексной формы ряда Фурье для сигналов с периодом T предельный переход к 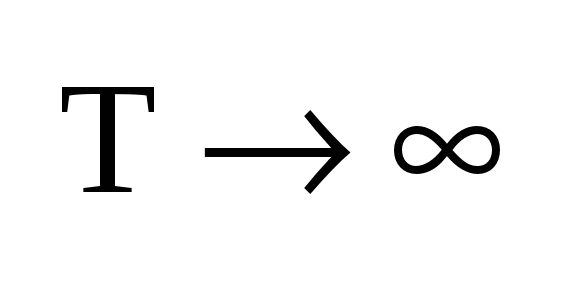 . При таком переходе интервалы между соседними частотами дискретного спектра . При таком переходе интервалы между соседними частотами дискретного спектра 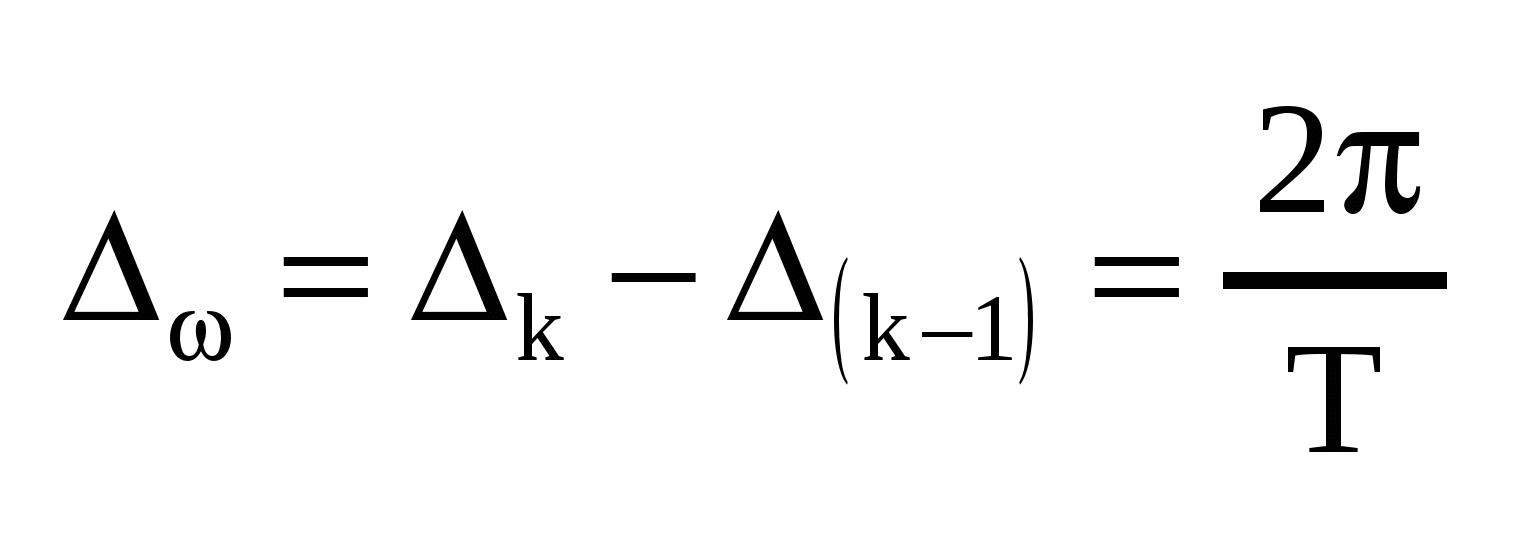 неограниченно уменьшаются, что приводит к непрерывному спектру, соотв-ему непериодическому сигналу. Однако его коэффициенты Фурье неограниченно уменьшаются, что приводит к непрерывному спектру, соотв-ему непериодическому сигналу. Однако его коэффициенты Фурье 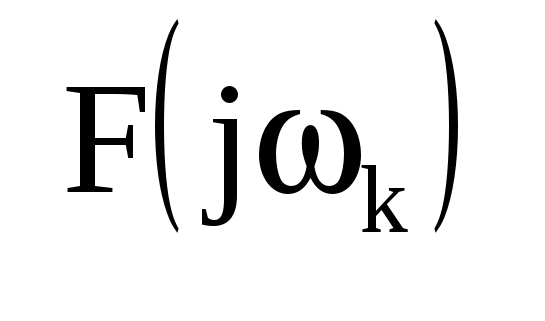 и амплитуды отдельных гармоник становятся бесконечно малыми. Поэтому при выполнении предельного перехода будем оперировать не с коэффициентами и амплитуды отдельных гармоник становятся бесконечно малыми. Поэтому при выполнении предельного перехода будем оперировать не с коэффициентами 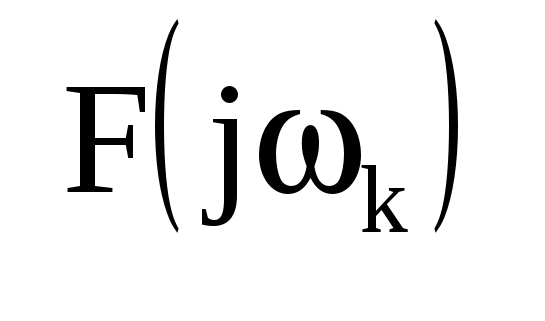 , а выразим через произведение , а выразим через произведение 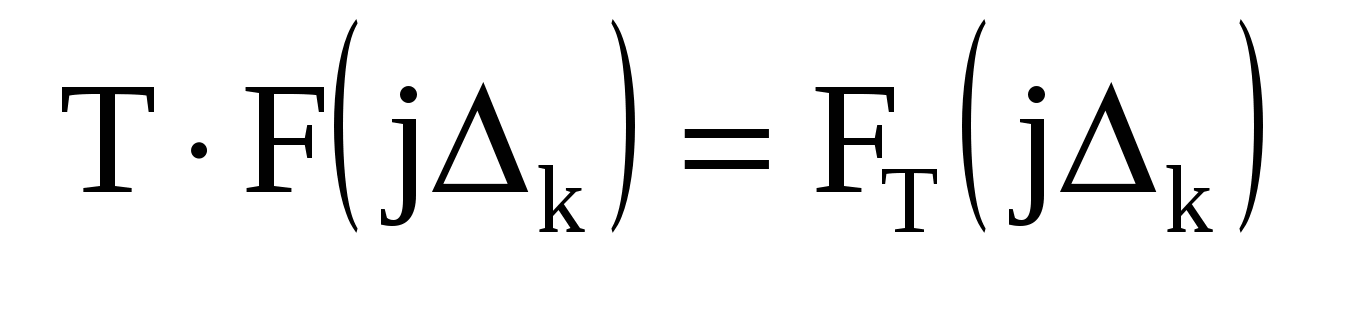 , сохраняющее конечное значение при , сохраняющее конечное значение при 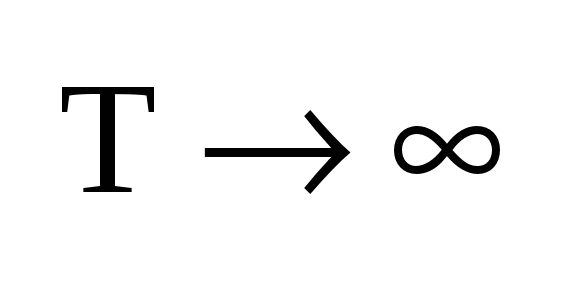 . Выполняя такую замену и учитывая связь . Выполняя такую замену и учитывая связь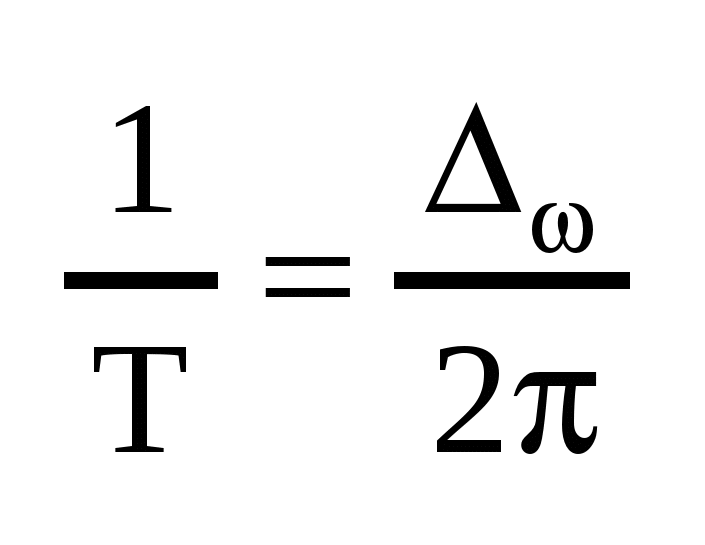 , перепшем: , перепшем:
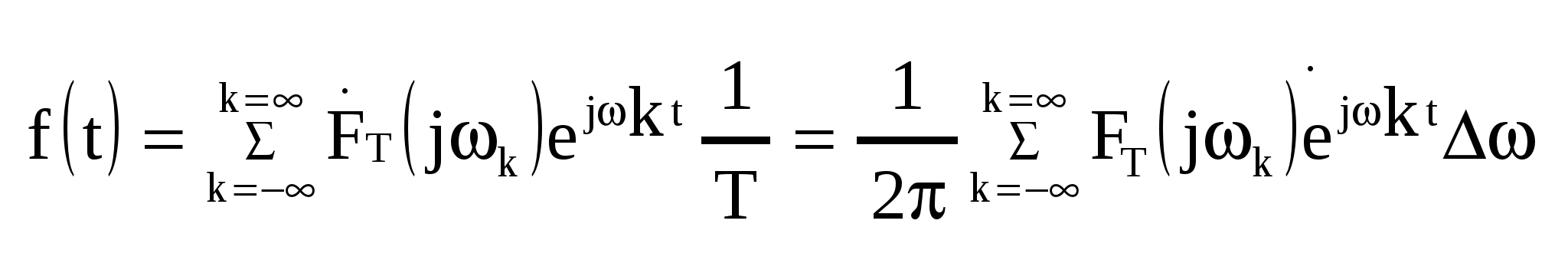 , ,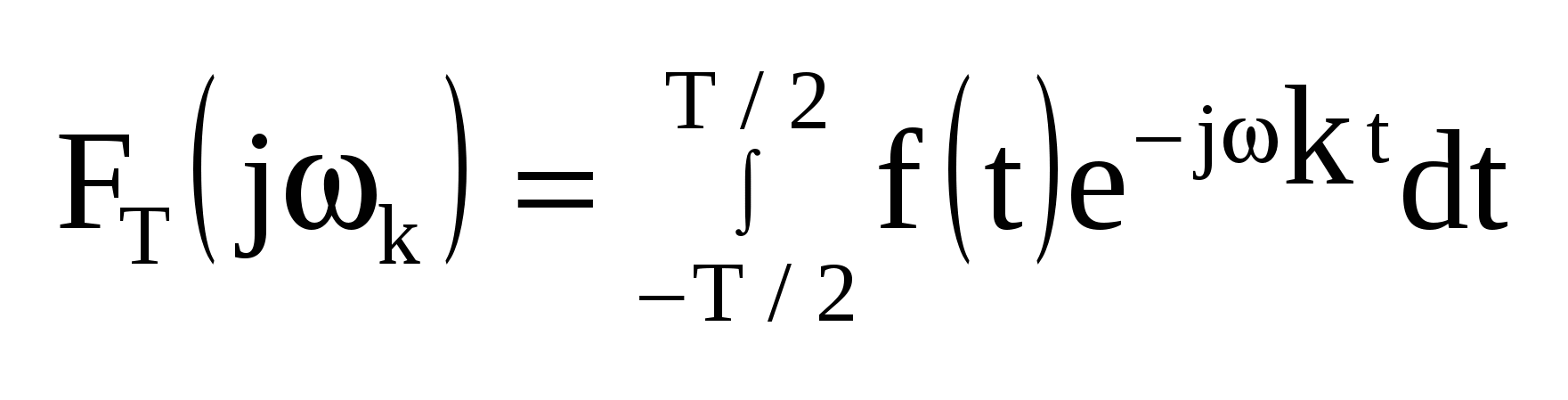 . .
Переходя к пределу при 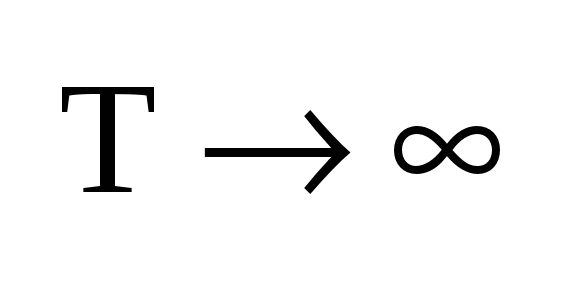 заменим заменим 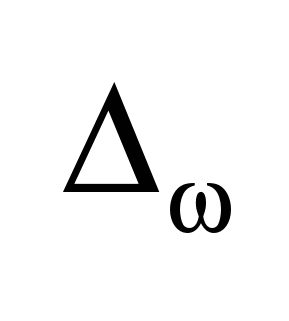 на бесконечно малую величину на бесконечно малую величину 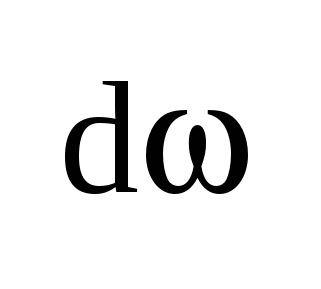 , а дискретные значения частоты , а дискретные значения частоты 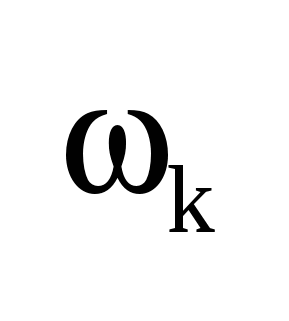 — на непрерывные — на непрерывные  , изменяющиеся в пределах от – , изменяющиеся в пределах от –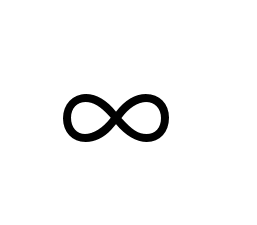 до + до + . В результате сумма в выражении для . В результате сумма в выражении для 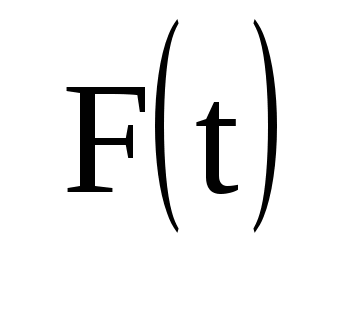 перейдет в интеграл. Заменяя обозначение перейдет в интеграл. Заменяя обозначение 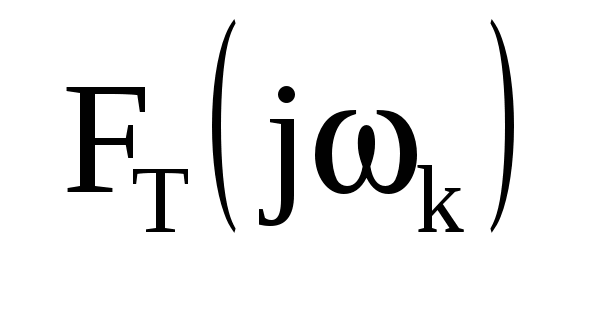 на на 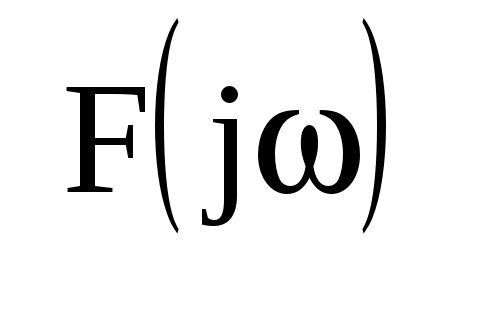 , получим для спектр. представления непериодического сигнала: , получим для спектр. представления непериодического сигнала: 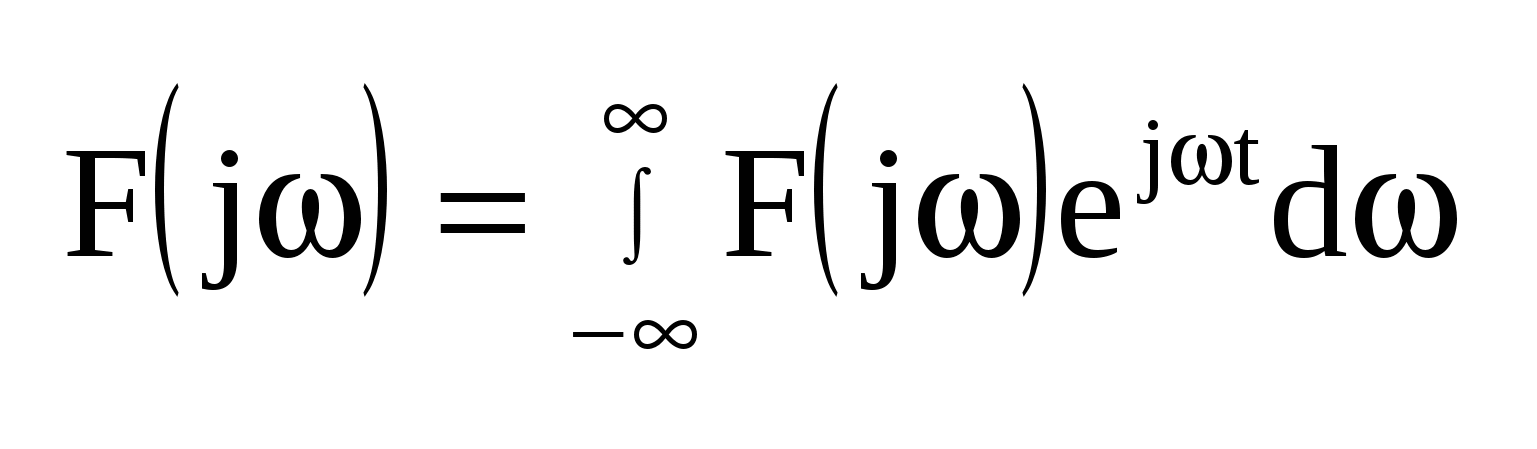 ; ;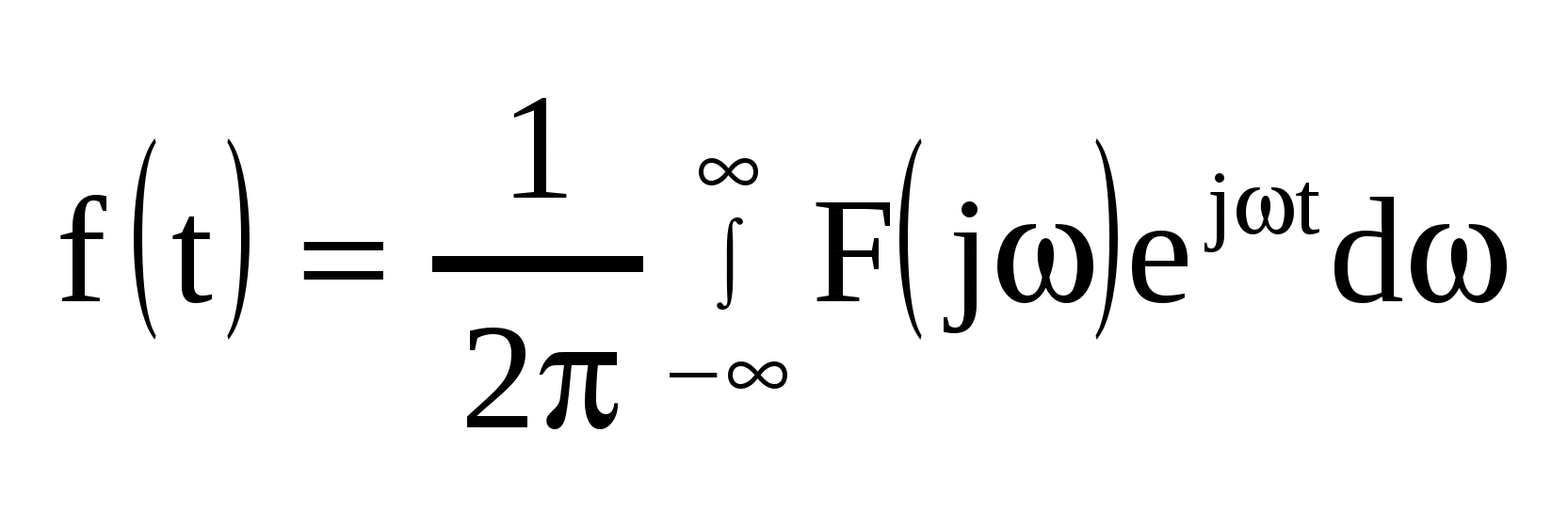 . Полученные формулы определяют прямое и обратное интегральные преобразования Фурье. С их помощью непериодическая функция времени . Полученные формулы определяют прямое и обратное интегральные преобразования Фурье. С их помощью непериодическая функция времени 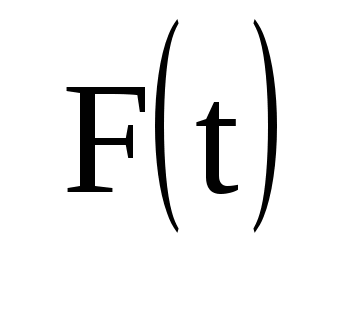 представляется совокупностью бесконечно большого числа синусоидальных составляющих с бесконечно малыми амплитудами представляется совокупностью бесконечно большого числа синусоидальных составляющих с бесконечно малыми амплитудами 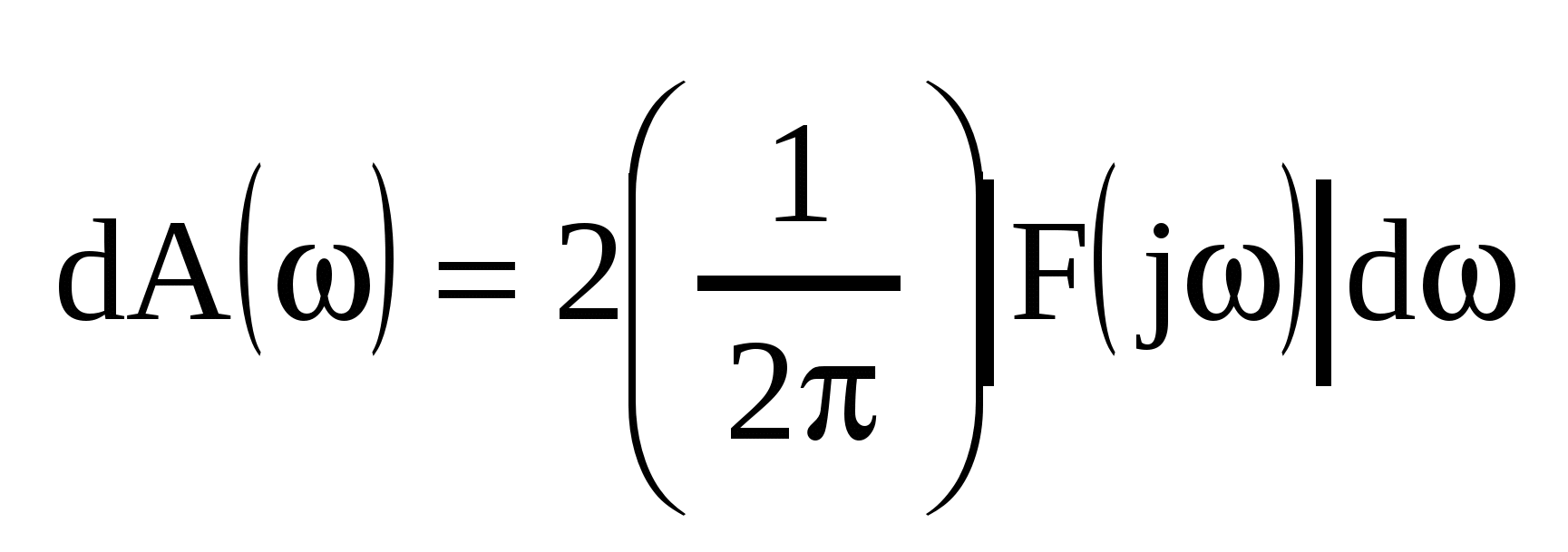 , частоты которых принимают любые значения от 0 до , частоты которых принимают любые значения от 0 до 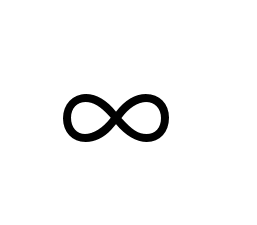 . Величина . Величина 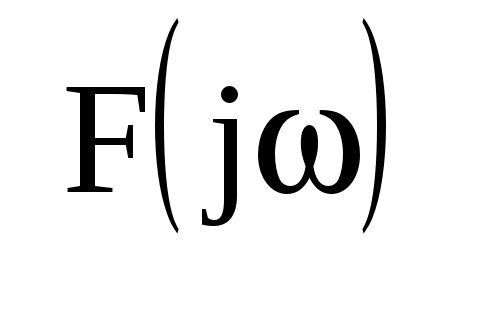 , характеризующая распределение отдельных составляющих в спектре сигнала, называется спектральной плотностью. , характеризующая распределение отдельных составляющих в спектре сигнала, называется спектральной плотностью.
|
59. Связь преобразований непериодических сигналов по Фурье и Лапласу.
|
60. Связь спектральных характеристик одиночного импульса и периодической после-довательности импульсов.
|
61. Спектральная характеристика одиночного прямоугольного импульса. Ширина спектра этого сигнала.
|
62. Амплитудный и фазовый спектры периодической последовательности прямоугольных импульсов. Представление рядом Фурье периодической последовательности прямоугольных импульсов.
|
63. Вычисление частотных характеристик электрических цепей. Экспериментальное определение этих характеристик.
|
64. Частотные характеристики электрической цепи, передающей электрический сигнал без искажения. Понятие о полосе пропускания электрической цепи.
|
65. Частотные характеристики идеальной дифференцирующей цепи.
|
66. Частотные характеристики реальной дифференцирующей RC-цепи.
|
67. Реакция реальной дифференцирующей RC-цепи на линейно-возрастающее воздействие.
|
68. Частотные характеристики идеальной интегрирующей цепи.
|
69. Частотные характеристики реальной интегрирующей RC-цепи.
|
70. Переходная характеристика реальной интегрирующей RC-цепи.
|
©
Жуковский Артём,
Астахов Антон,
Мездрогин Дима
Новик Саша
Сорокин Андрей
Сделано для группы 6151 (http://6151.spb.ru)
|
 Скачать 4.69 Mb.
Скачать 4.69 Mb.