|
|
1. Понятие о токе, напряжении, мощности, энергии
1. Понятие о токе, напряжении, мощности, энергии.
Электрическим током называется упорядоченное движение частиц - носителей тока. Постоянный ток – ток неизменимый во времени. Электрический ток характеризуется силой тока.
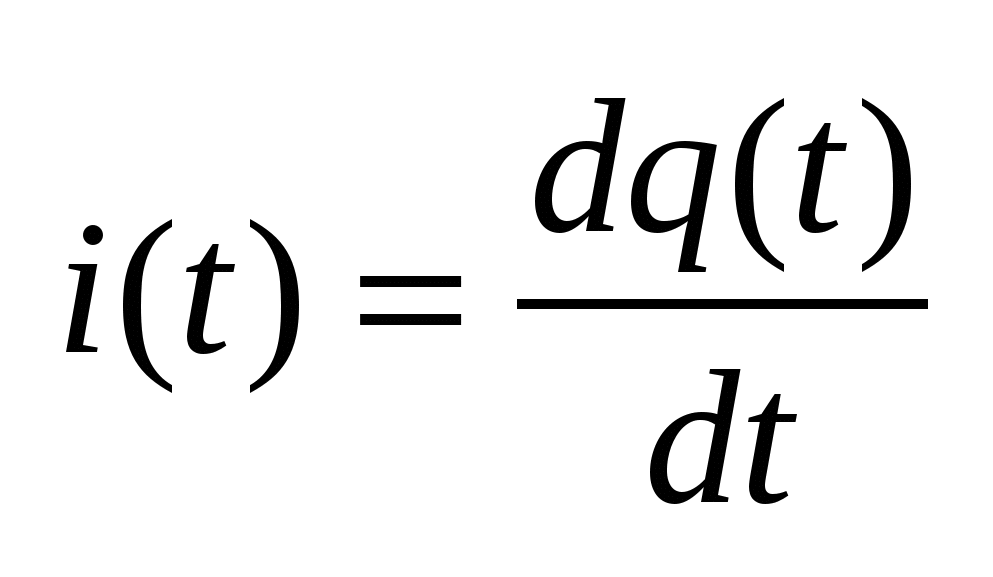 , где , где 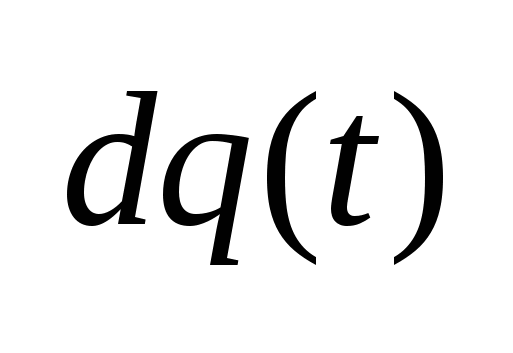 - величина заряда, т.е. - величина заряда, т.е. 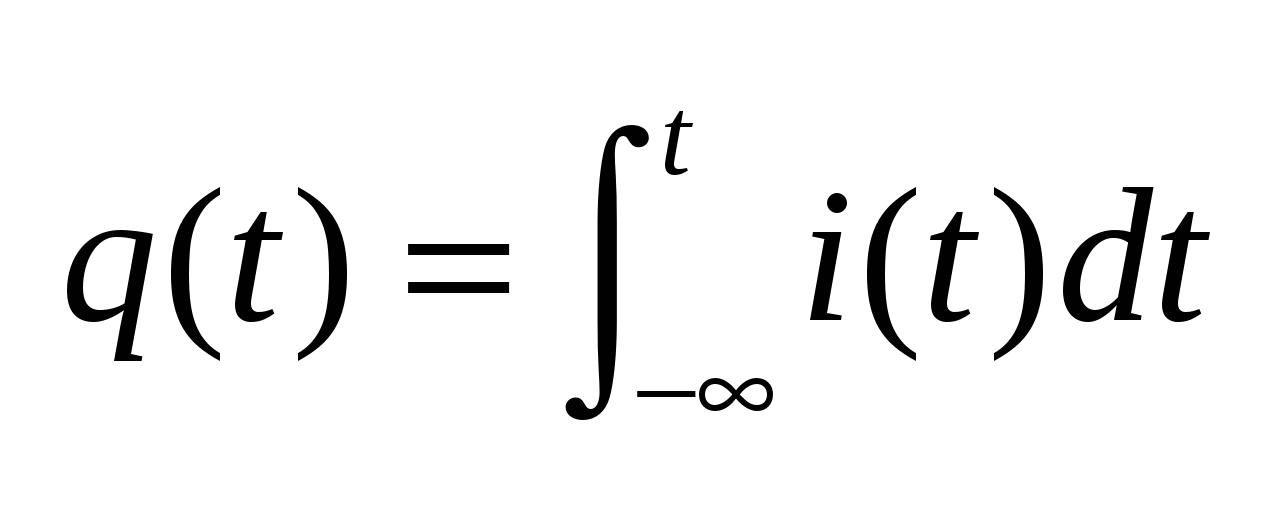 . Помимо величины существует и направление тока, связанное с перемещением положительных зарядов (если I = 2A, то имеются ввиду положит заряды; I=-2A – отрицательные). Направления токов выбираются произвольно. . Помимо величины существует и направление тока, связанное с перемещением положительных зарядов (если I = 2A, то имеются ввиду положит заряды; I=-2A – отрицательные). Направления токов выбираются произвольно.
 При перемещении зарядов в цепи выделяется или потребляется энергия. При перемещении зарядов в цепи выделяется или потребляется энергия. 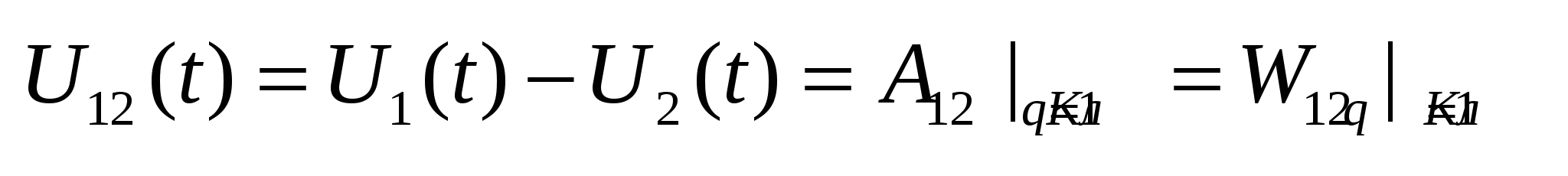 . При расчете цепей рекомендуется выбирать согласованное включение элементов цепи. . При расчете цепей рекомендуется выбирать согласованное включение элементов цепи.
При перемещении элементарного заряда выделяется следующая энергия:
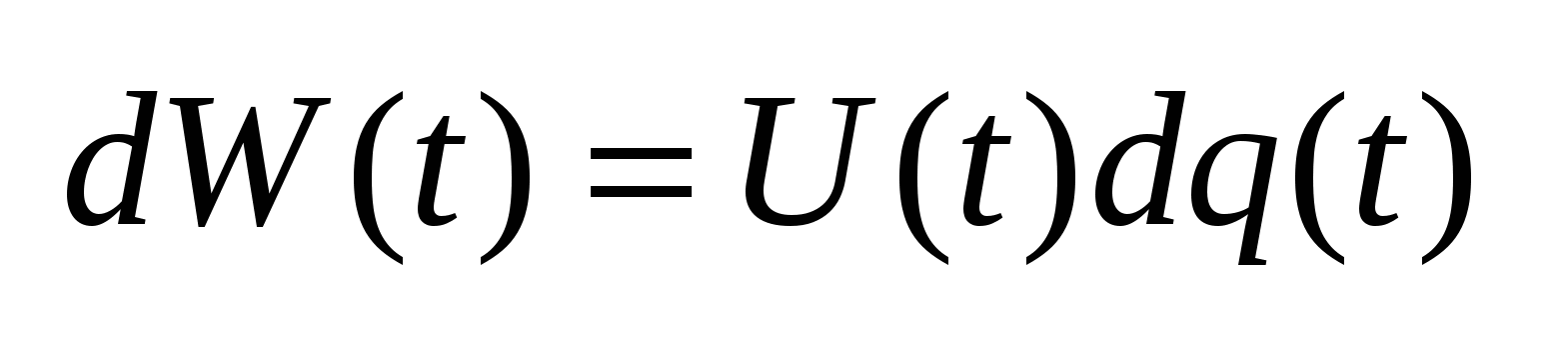 (1). Мощность – скорость потребления энергии элементом: (1). Мощность – скорость потребления энергии элементом: 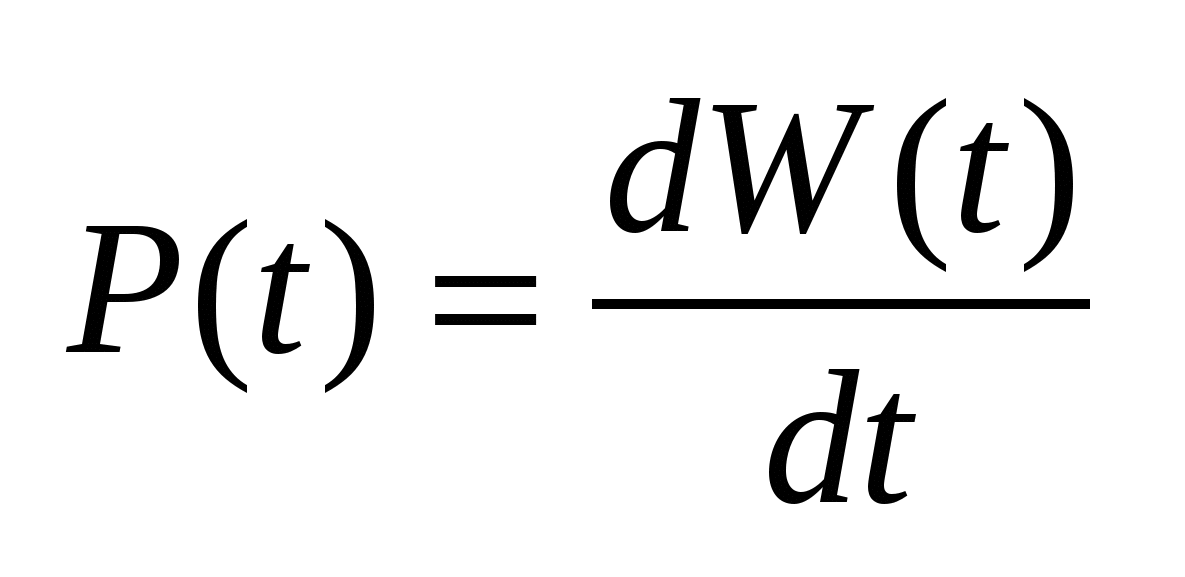 (2). Из (1)и(2) => (2). Из (1)и(2) => 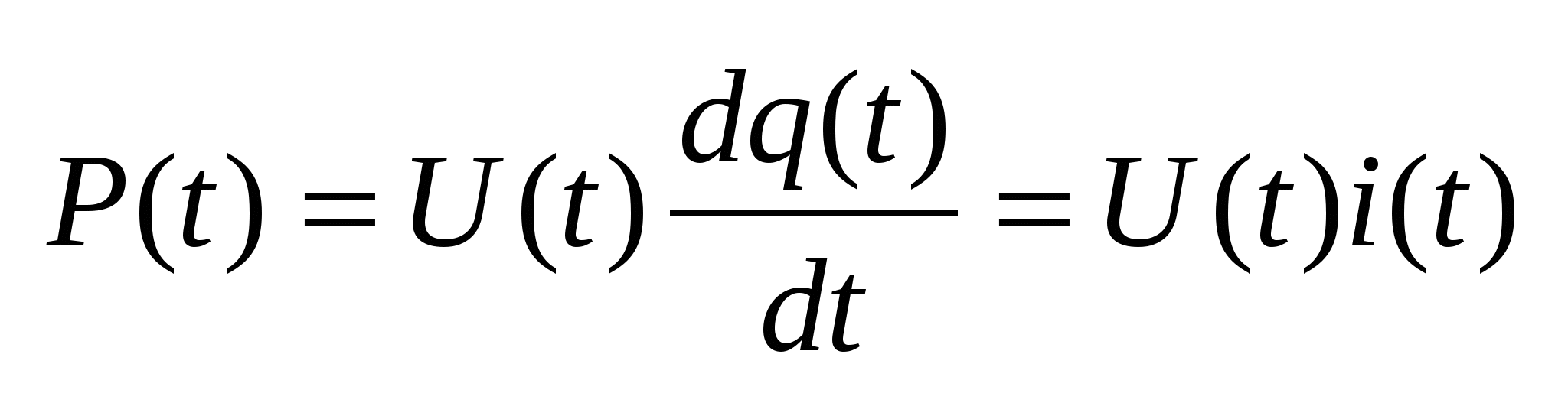 . Из (2): . Из (2):
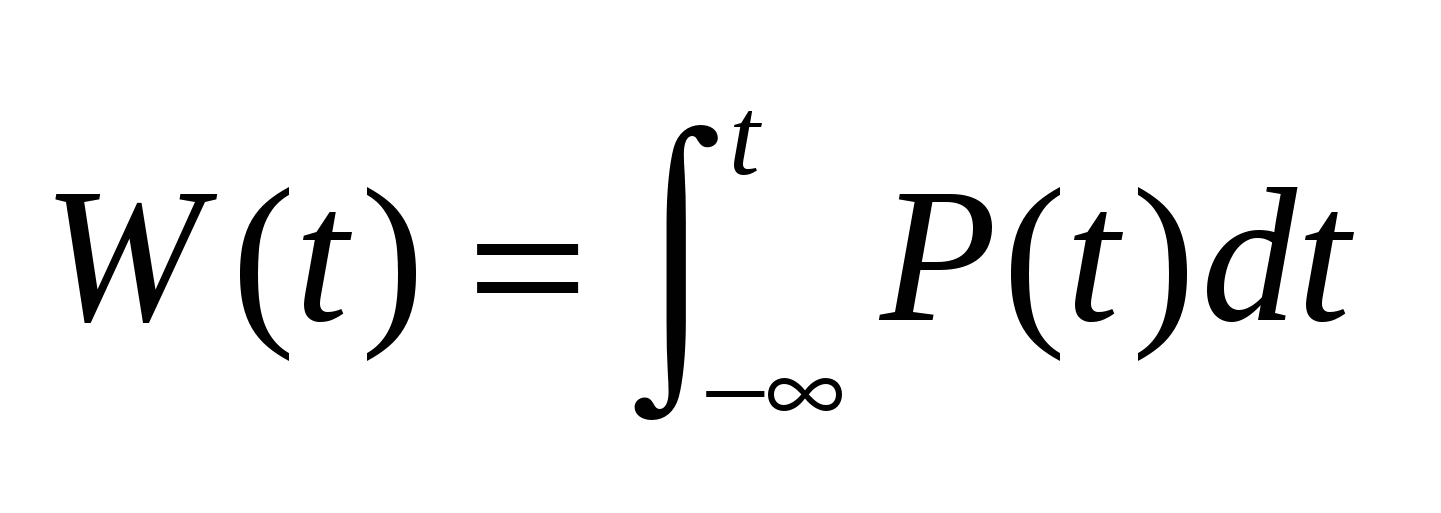 . Элемент называется пассивным, если в любой момент времени их энергия положительна, т.е. . Элемент называется пассивным, если в любой момент времени их энергия положительна, т.е. 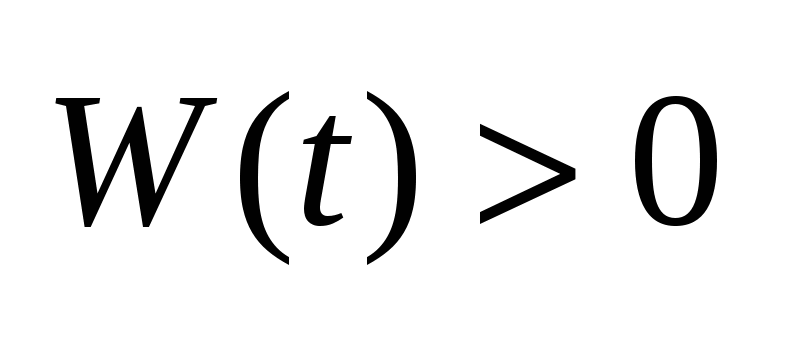 . Если на элементе его мощность >0, то элемент потребляет энергию, в противном случае – отдает . Если на элементе его мощность >0, то элемент потребляет энергию, в противном случае – отдает
|
2. Идеализированный резистивный элемент электрической цепи и его характеристики.
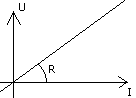
Резистивный элемент характеризуется своим сопротивлением. 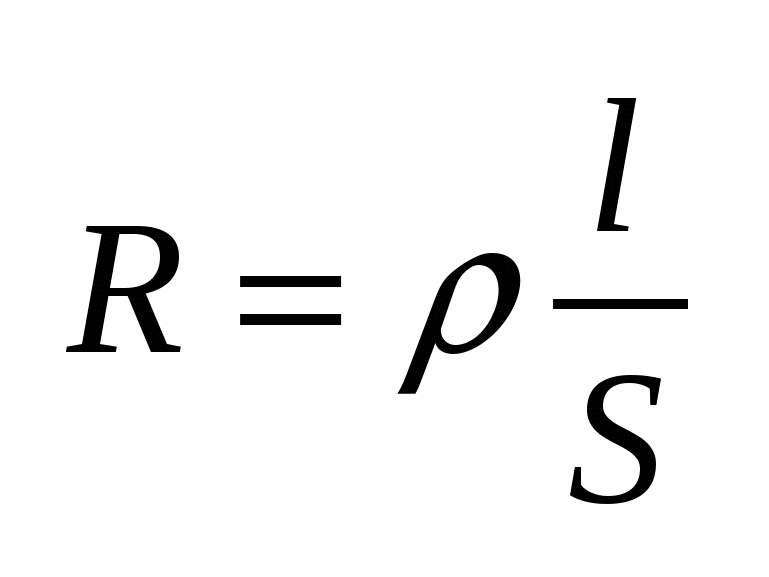 , где , где 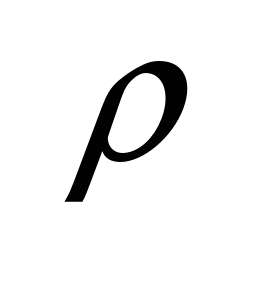 - удельное сопротивление, зависящая от свойств материала. Закон Ома для R-элемента: - удельное сопротивление, зависящая от свойств материала. Закон Ома для R-элемента: 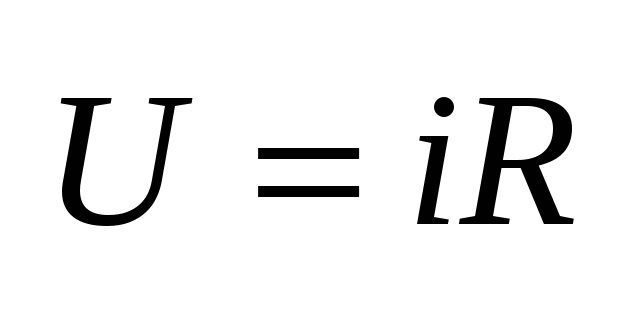 . ВАХ R-элемента ( . ВАХ R-элемента (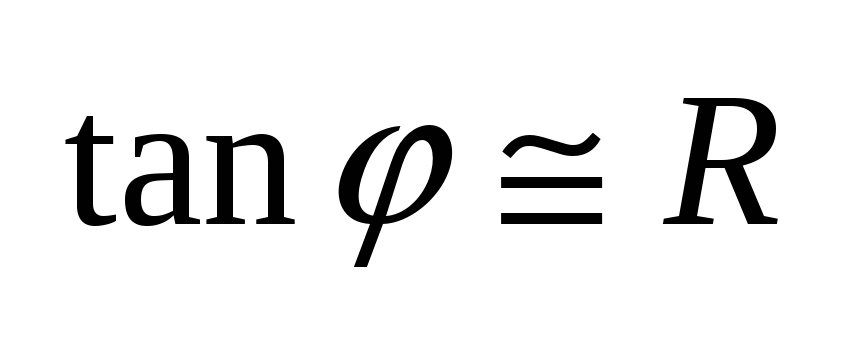 ) )
G – проводимость = 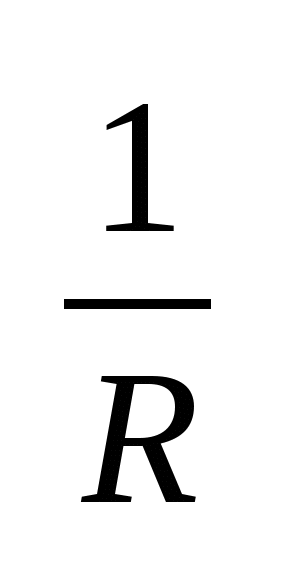 [Сим]. Мощность на R-элементе [Сим]. Мощность на R-элементе
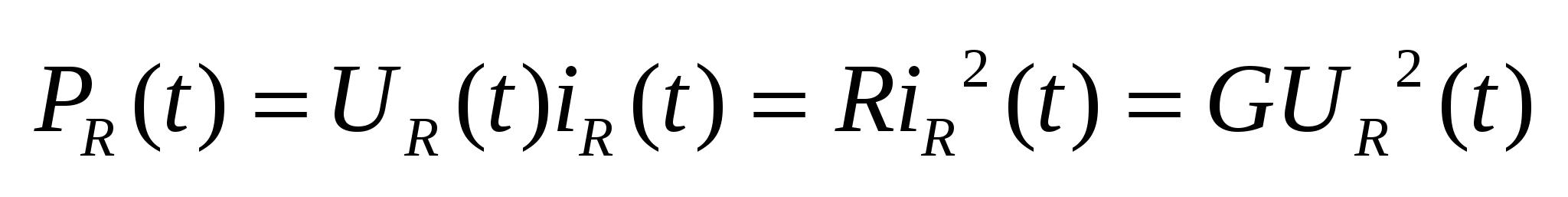 . R-элемент всегда потребляет энегию, т.к. . R-элемент всегда потребляет энегию, т.к. 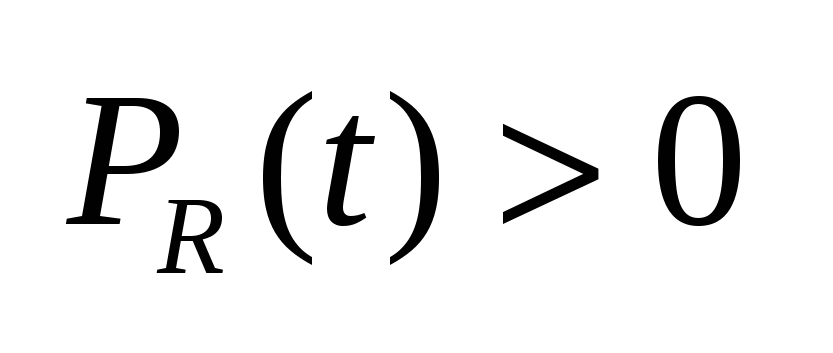 (ВСЕГДА). (ВСЕГДА). 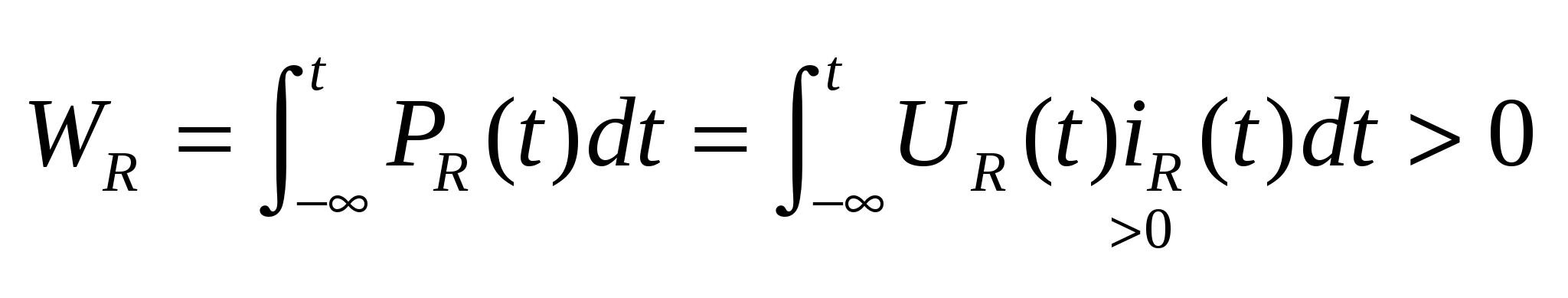 => R-элемент – пассивен. => R-элемент – пассивен.
|
3. Идеализированный индуктивный элемент электрической цепи и его характеристики.
Индуктивность — идеализированное устройство, имеющее два зажима, единственным ЭМ процессом в котором является запасание и полный возврат энергии магнитного поля. Отсюда следует, что для описания индуктивности используется ее ампер-веберная характеристика 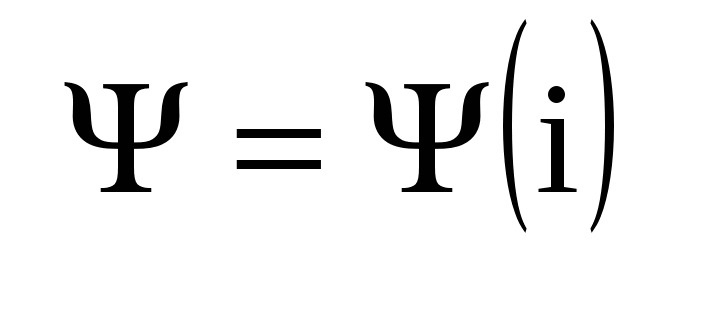 . Характеристика может быть сделана практически любой; нелинейные характеристики аппроксимируют полиномом. . Характеристика может быть сделана практически любой; нелинейные характеристики аппроксимируют полиномом. 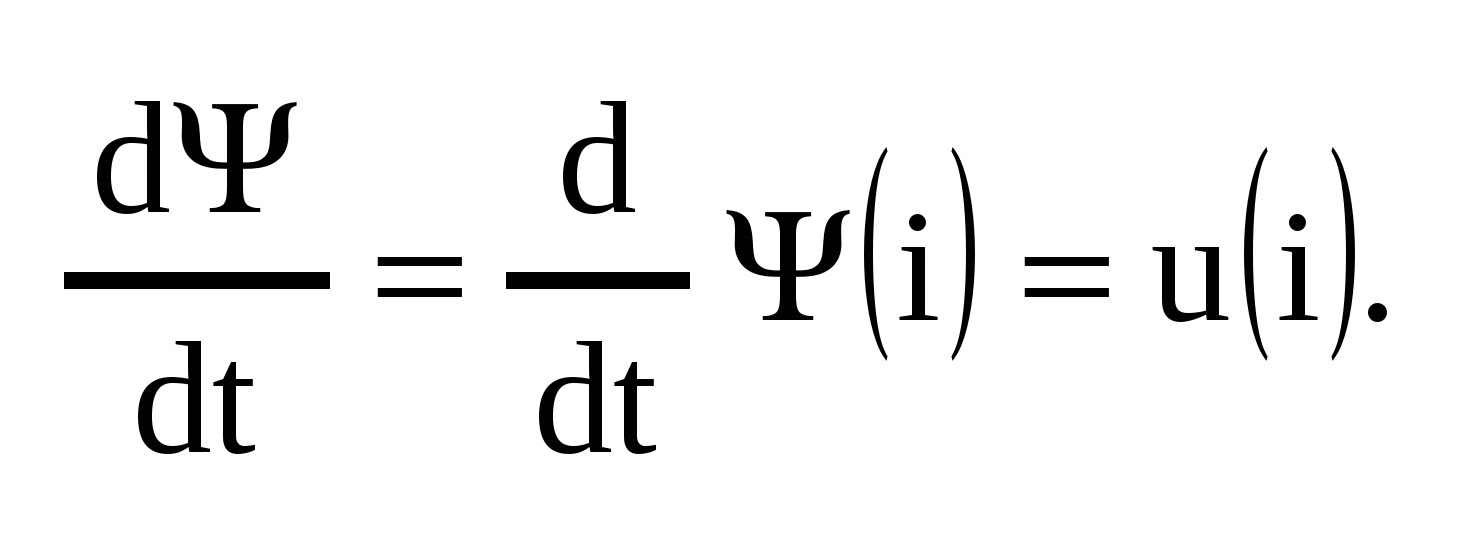
Если речь идет о линейной индуктивности, то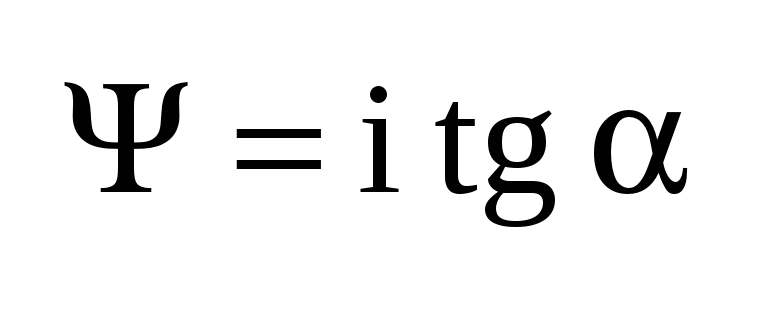 и и
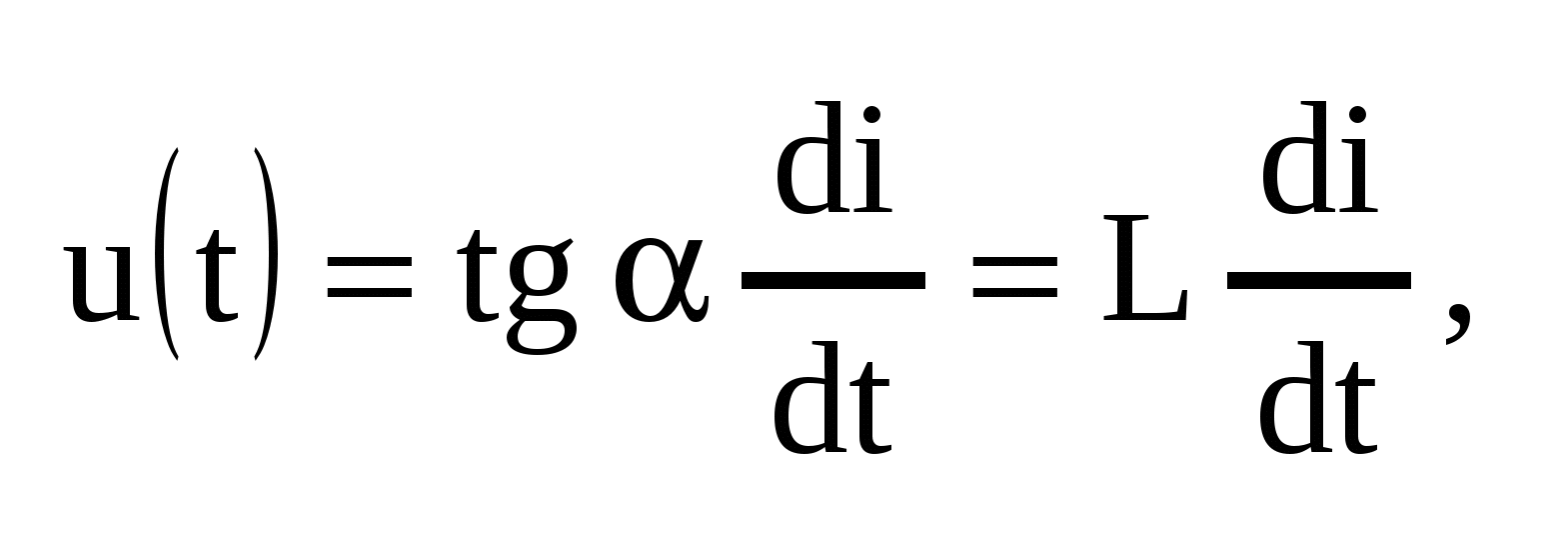
где коэффициент L называют индуктивностью. Размерность [L] = Гн. Можно также записать соотношение для линейной емкости в интегральной форме: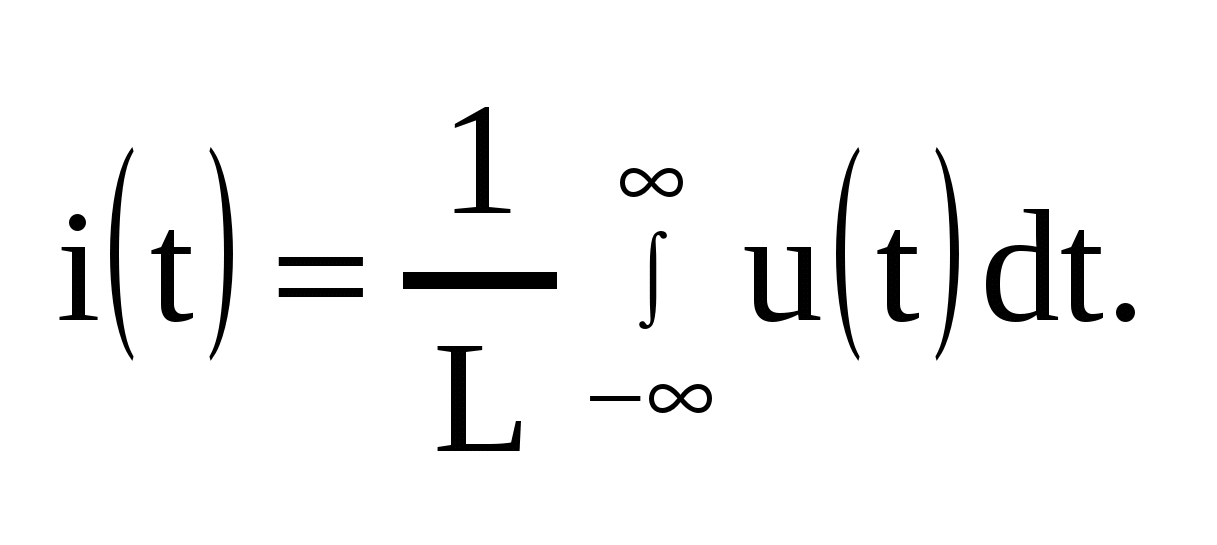
Сделав те же подстановки, что и для емкости, получим
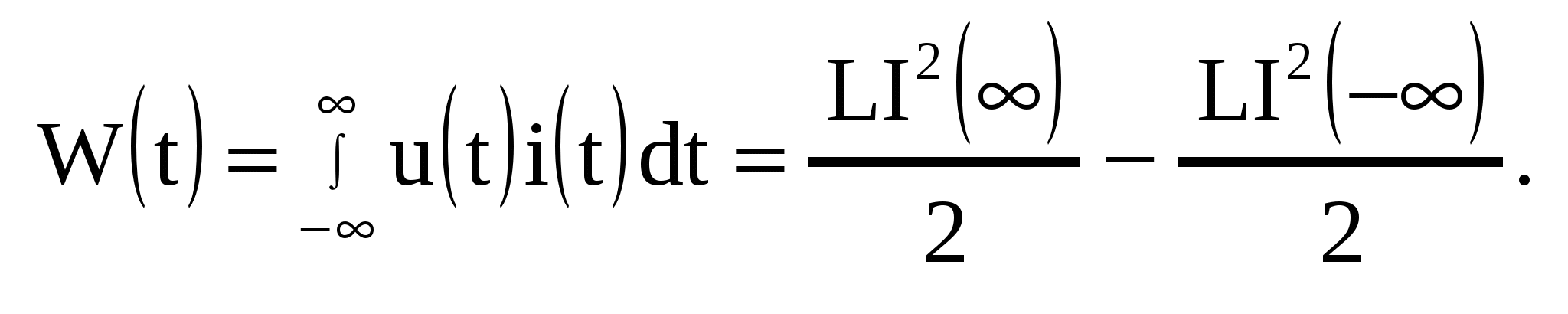
Положив (что вполне естественно) I(−∞) = 0, получим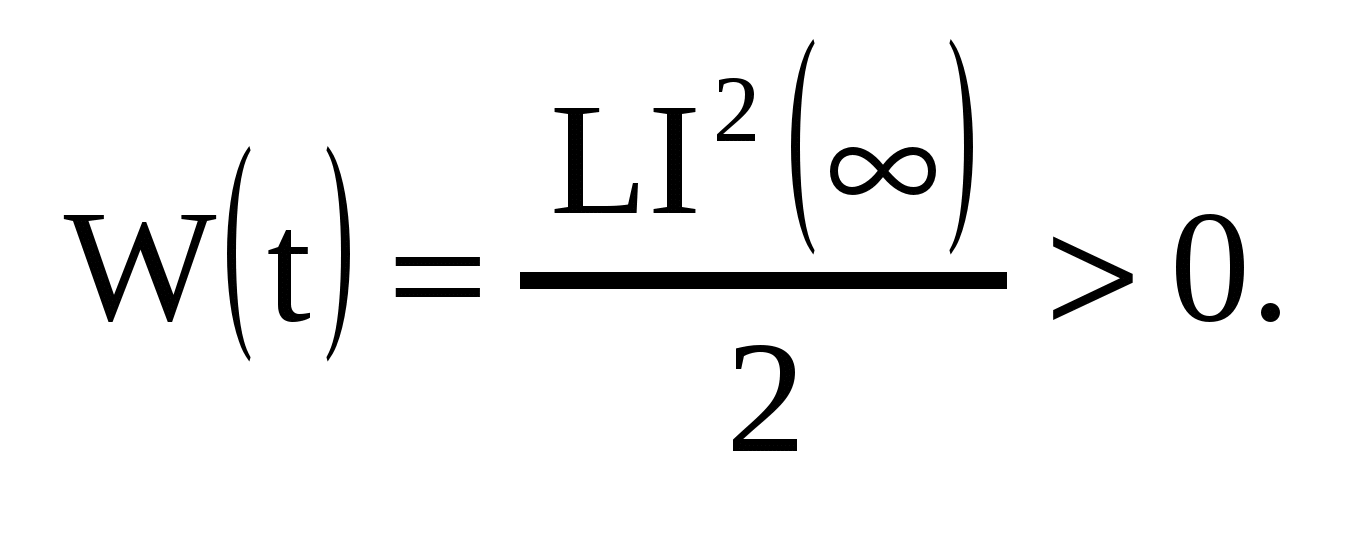
Мощность при этом равна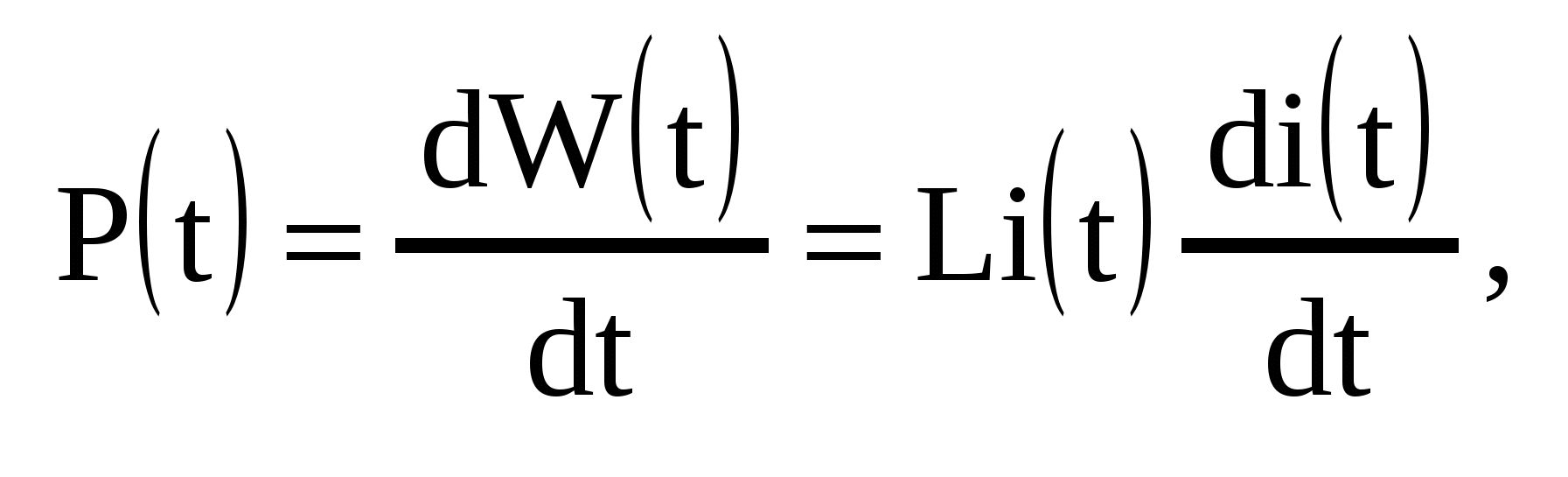
и может быть как положительной, так и отрицательной. Таким образом, индуктивность запасает магнитную энергию и полностью ее отдает.
Обозначение индуктивности
|
4. Идеализированный емкостной элемент электрической цепи и его характеристики.
Емкость — идеализированное устройство, имеющее два зажима, единственным ЭМ процессом в котором является запасание и полный возврат электрической энергии. Отсюда следует, что емкость описывается вольт-кулоновой характеристикой 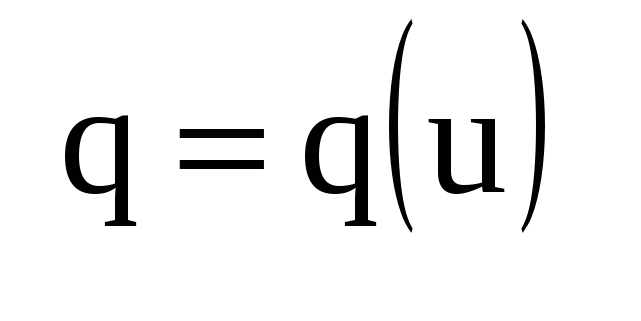 . .
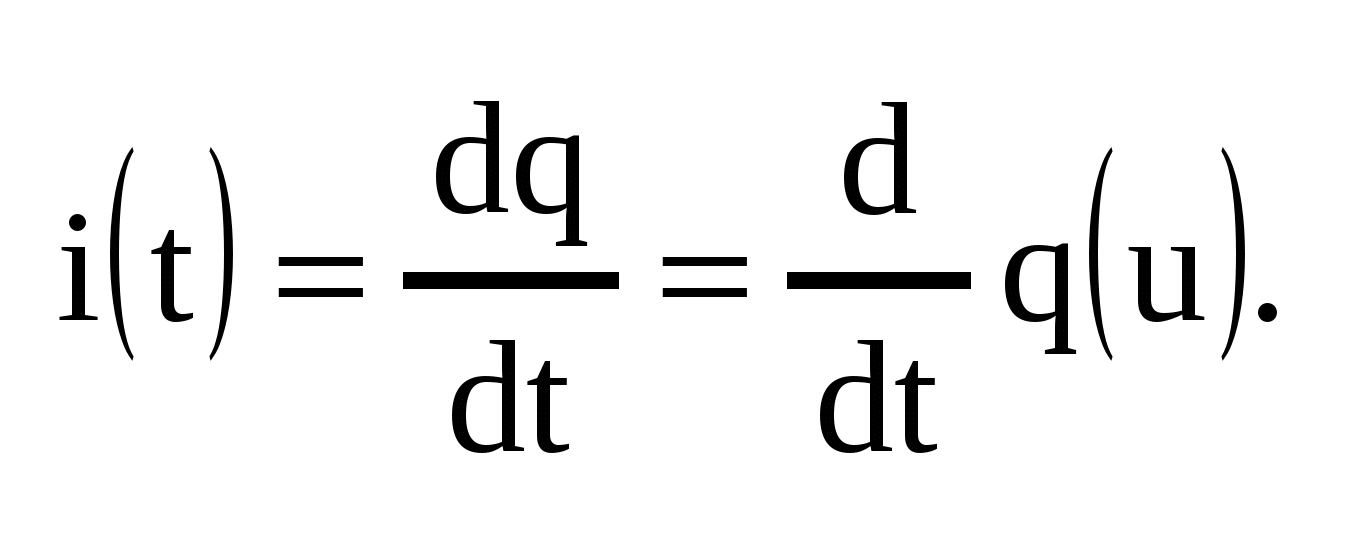
Если мы рассматриваем линейную емкость , то 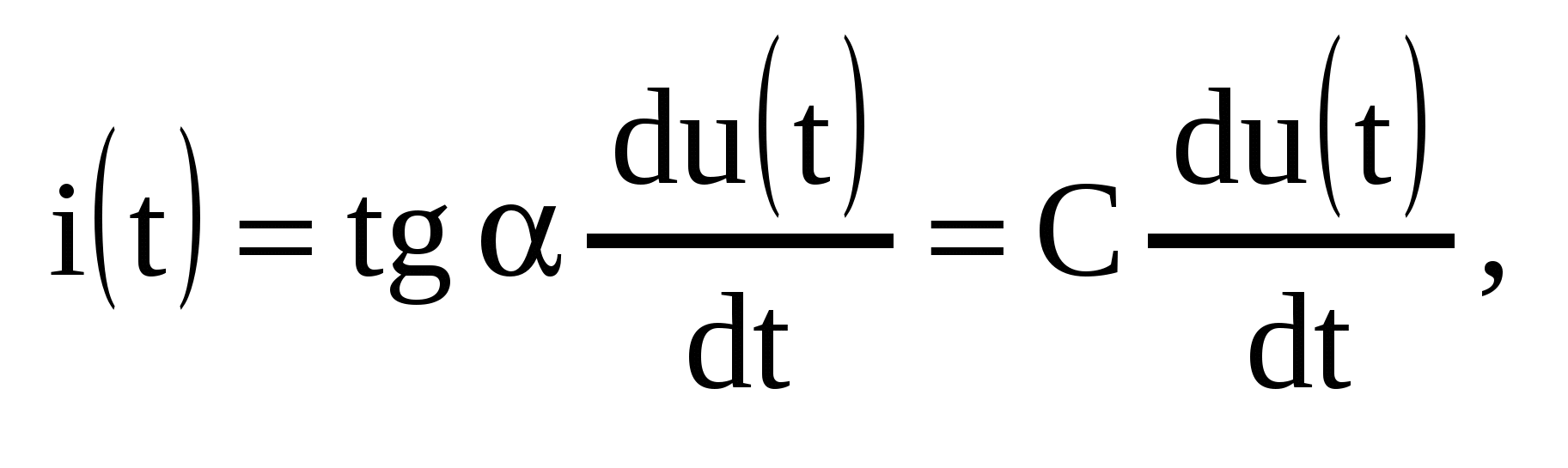
где коэффициент C называют емкостью. Размерность [C] = Ф. Можно также записать соотношение для линейной емкости в интегральной форме
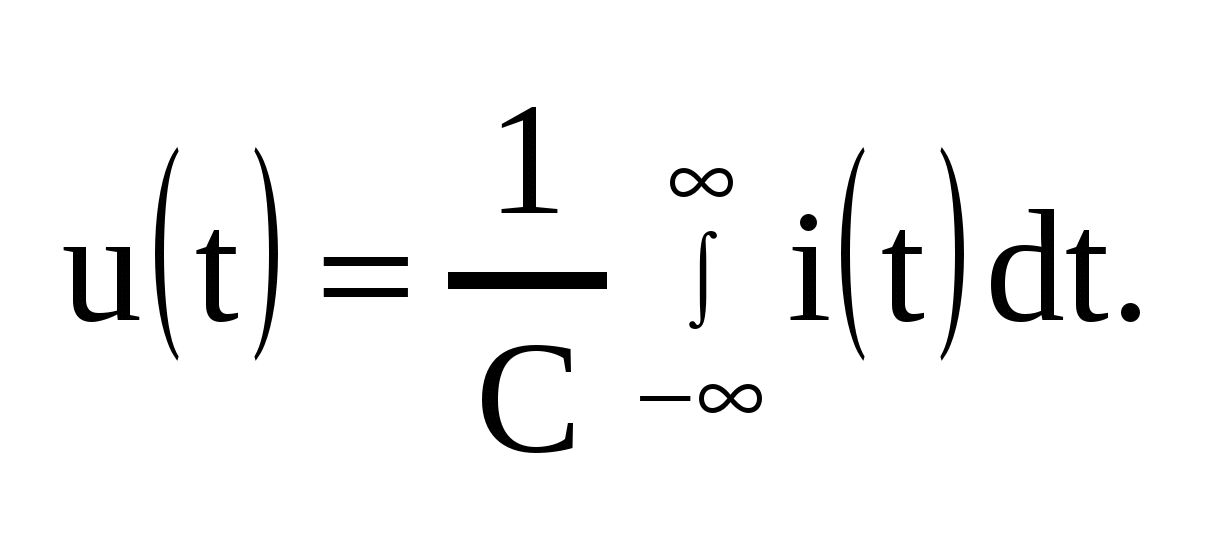
Энергия емкости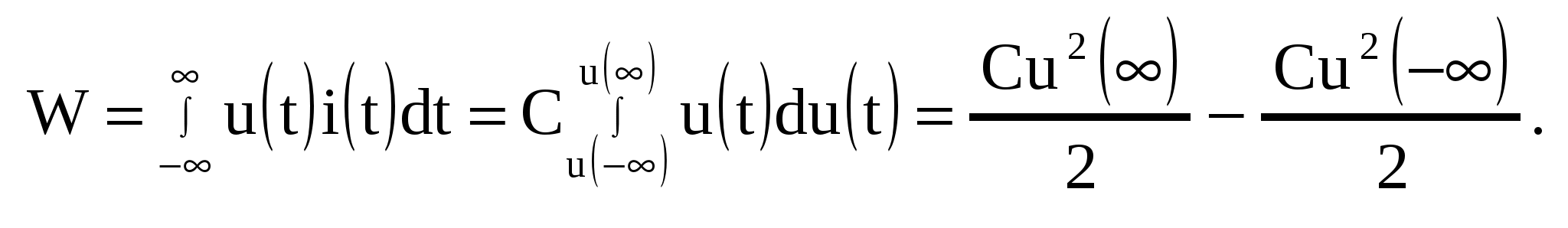
Положив, что вначале емкость не была заряжена: 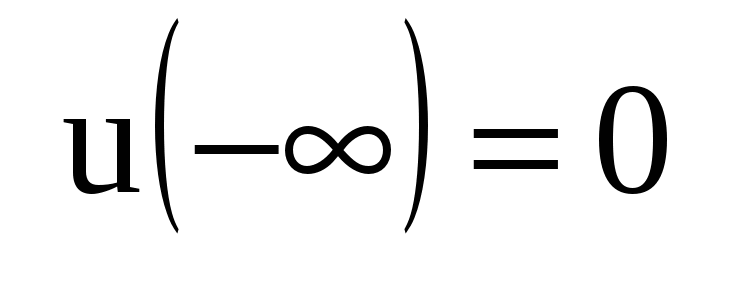 , получим , получим
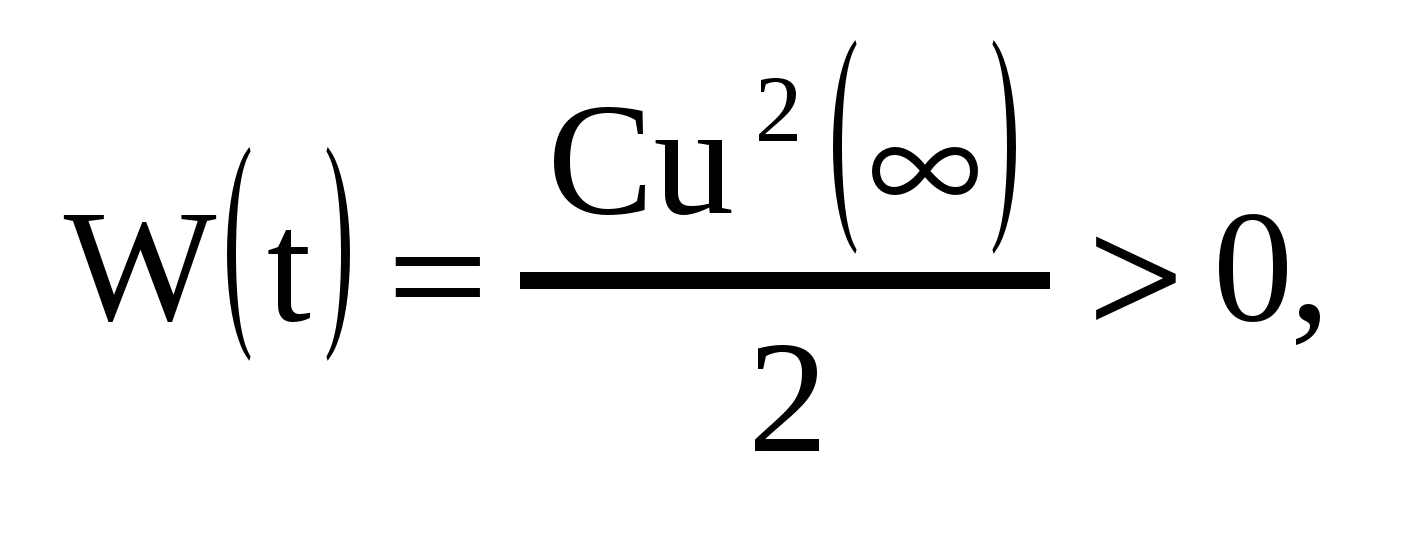 т.е., емкость производит запасание электрической энергии. Мощность равна т.е., емкость производит запасание электрической энергии. Мощность равна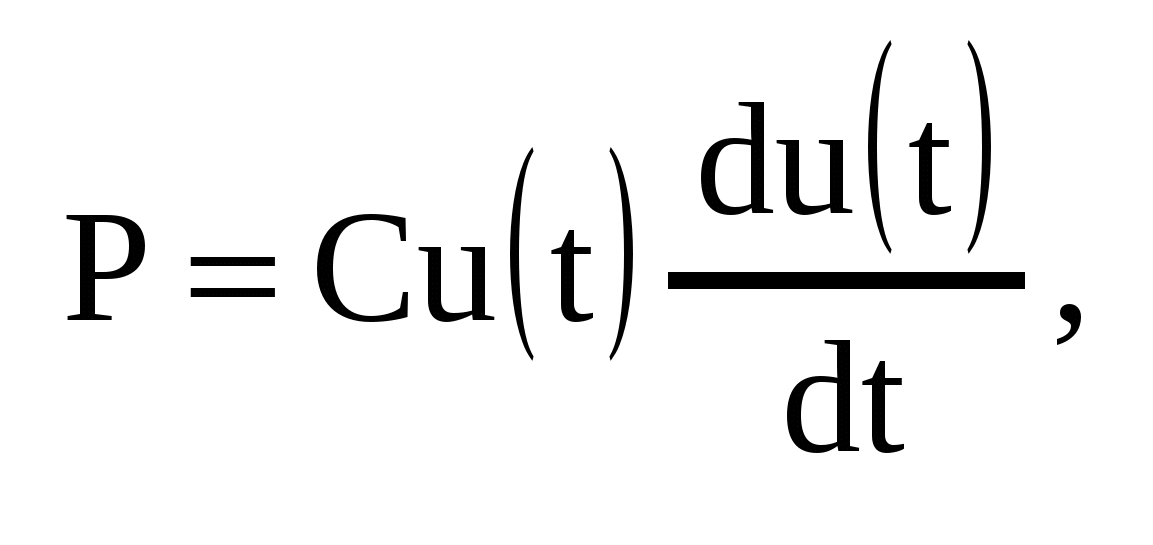
и может быть как положительной, так и отрицательной. Т.е., емкость запасает электрическую энергию и полностью ее отдает.
Обозначение емкости
|
5. Понятие об идеальном и реальном источниках напряжения.
Реальные источники электрической энергии имеет ЭДС 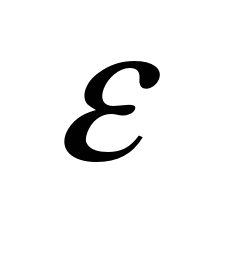 и внутреннее сопротивление и внутреннее сопротивление 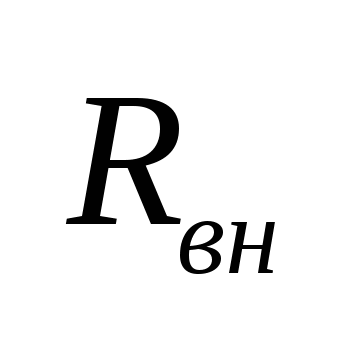 . Тогда сопротивление на его зажимах: . Тогда сопротивление на его зажимах: 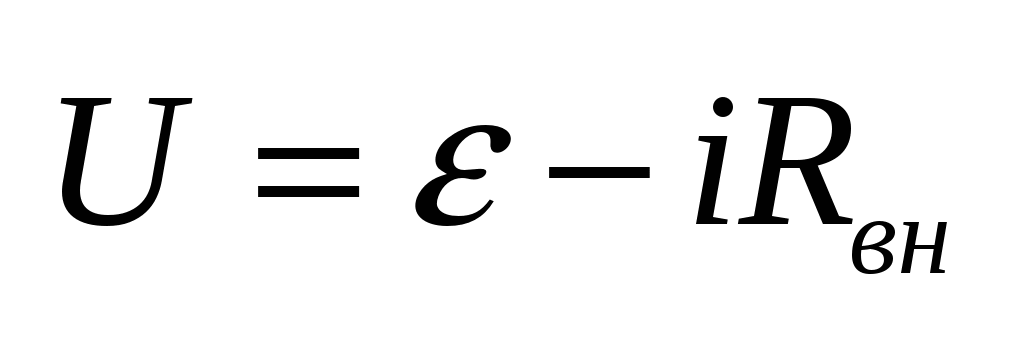 . Если по этому источнику будет протекать ток i, то напряжение будет убывать. . Если по этому источнику будет протекать ток i, то напряжение будет убывать.
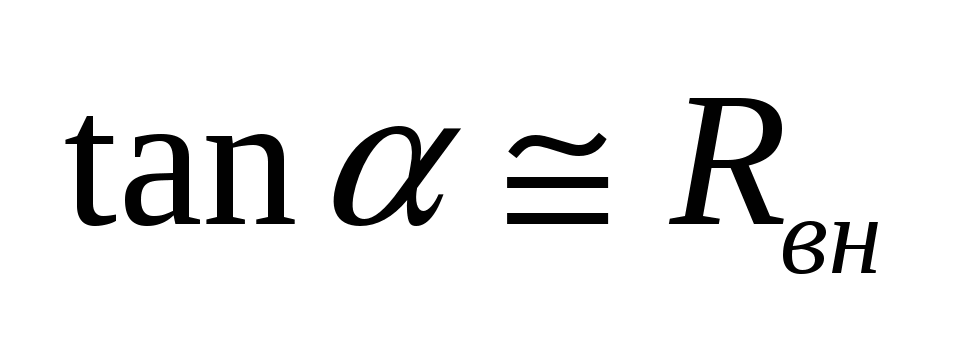 . Рассмотрим два предельных случая: . Рассмотрим два предельных случая:
1. 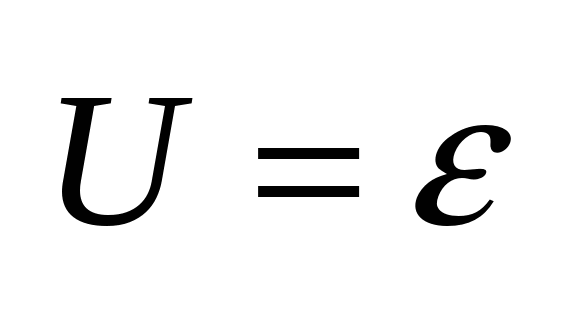 , т.е. напряжение не зависит от протекающего через него тока ( , т.е. напряжение не зависит от протекающего через него тока (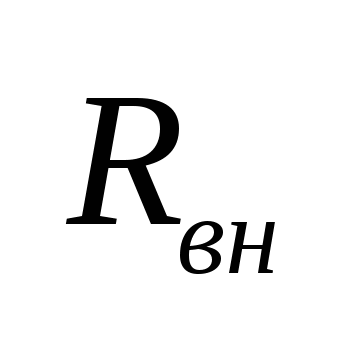 =0). Такой источник называется источником напряжения. =0). Такой источник называется источником напряжения.
2. Пусть 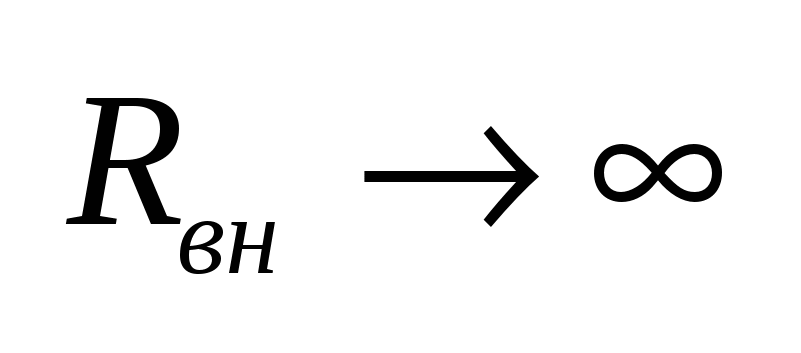 и и 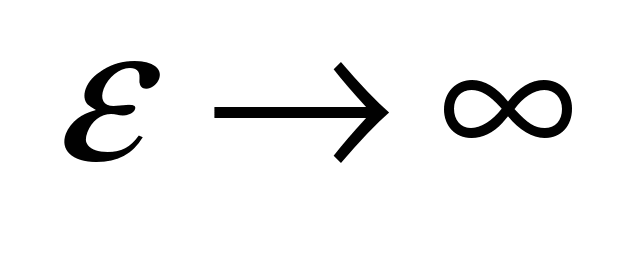 , тогда , тогда 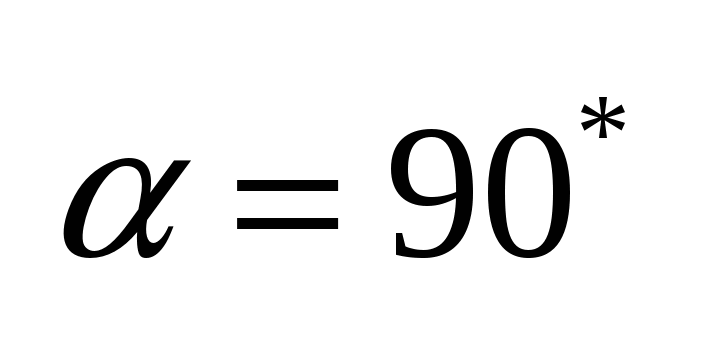 и мы получим, что и мы получим, что 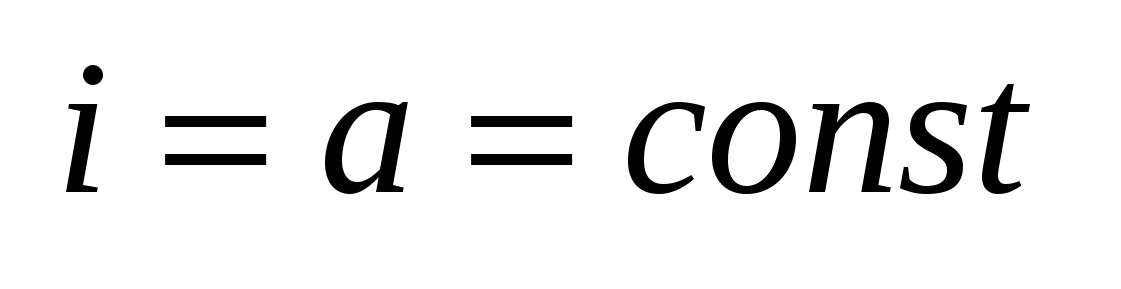 , где а – некоторое число. Такой источник называется источником тока. , где а – некоторое число. Такой источник называется источником тока.
|
6. Понятие об идеальном и реальном источниках тока.
Реальные источники электрической энергии имеет ЭДС 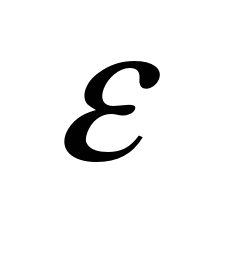 и внутреннее сопротивление и внутреннее сопротивление 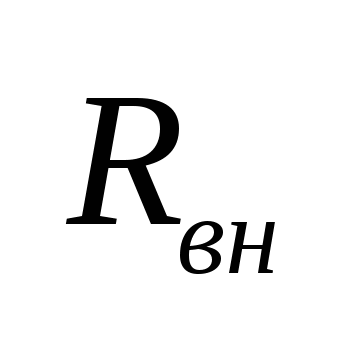 . Тогда сопротивление на его зажимах: . Тогда сопротивление на его зажимах: 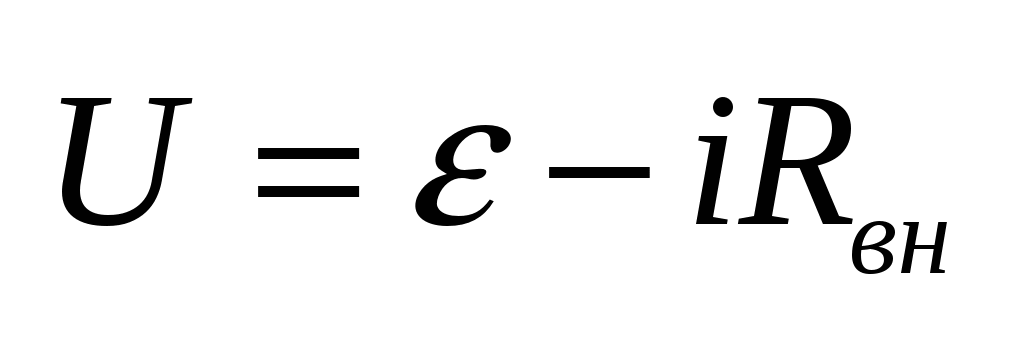 . Если по этому источнику будет протекать ток i, то напряжение будет убывать. . Если по этому источнику будет протекать ток i, то напряжение будет убывать.
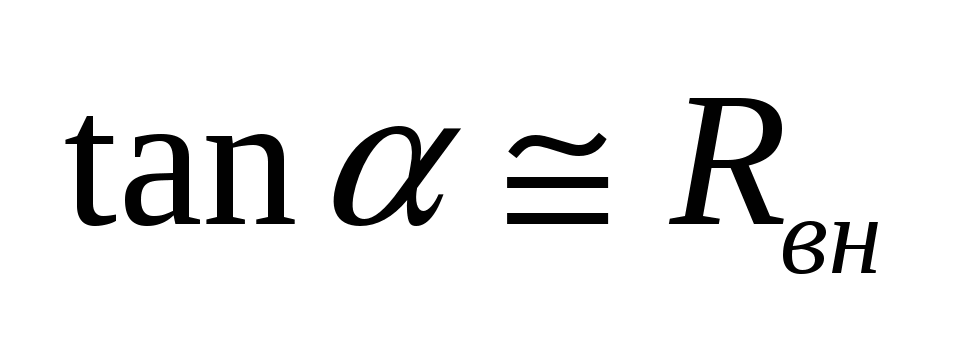 . Рассмотрим два предельных случая: . Рассмотрим два предельных случая:
1. 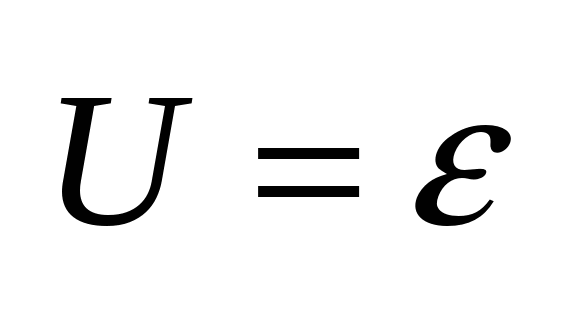 , т.е. напряжение не зависит от протекающего через него тока ( , т.е. напряжение не зависит от протекающего через него тока (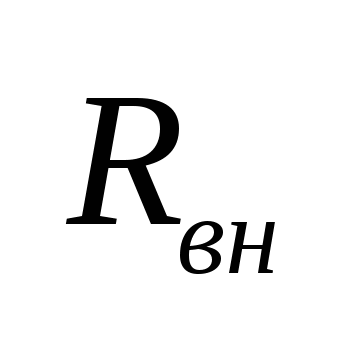 =0). Такой источник называется источником напряжения. =0). Такой источник называется источником напряжения.
2. Пусть 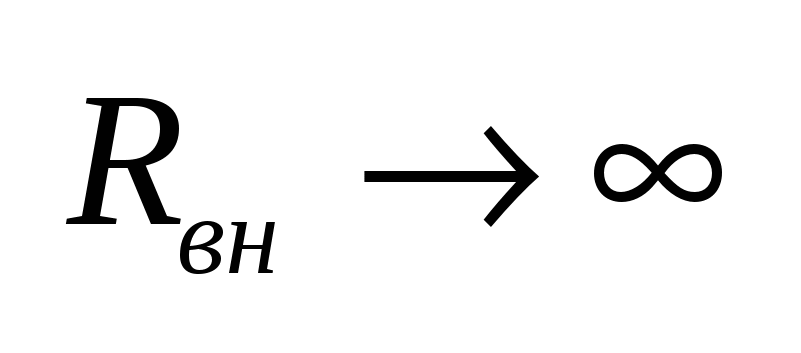 и и 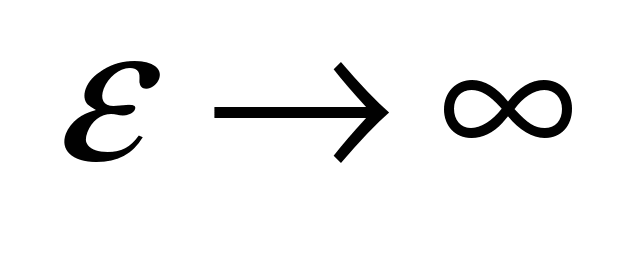 , тогда , тогда 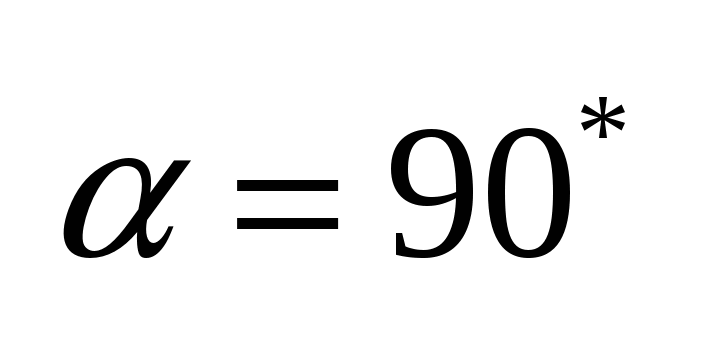 и мы получим, что и мы получим, что 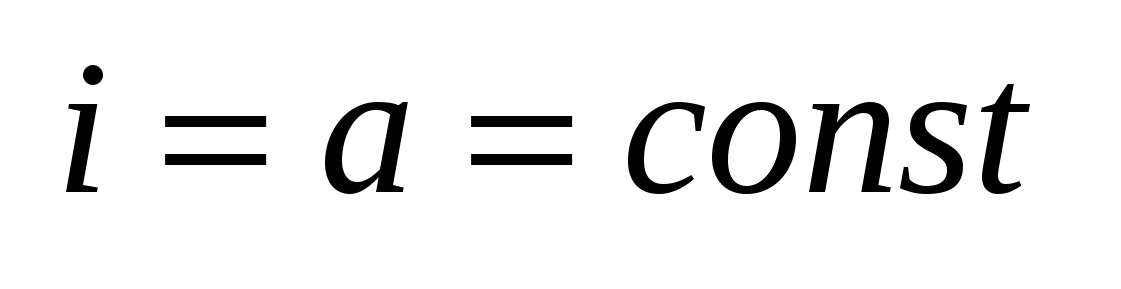 , где а – некоторое число. Такой источник называется источником тока. , где а – некоторое число. Такой источник называется источником тока.
|
7. Эквивалентные преобразования источников.
Эквивалентным называется преобразование, при котором напряжения и токи в частях схемы, не подвергшихся преобразованию, не меняются.
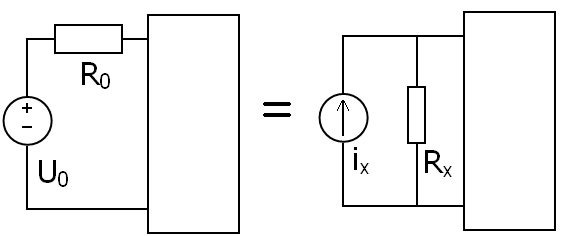
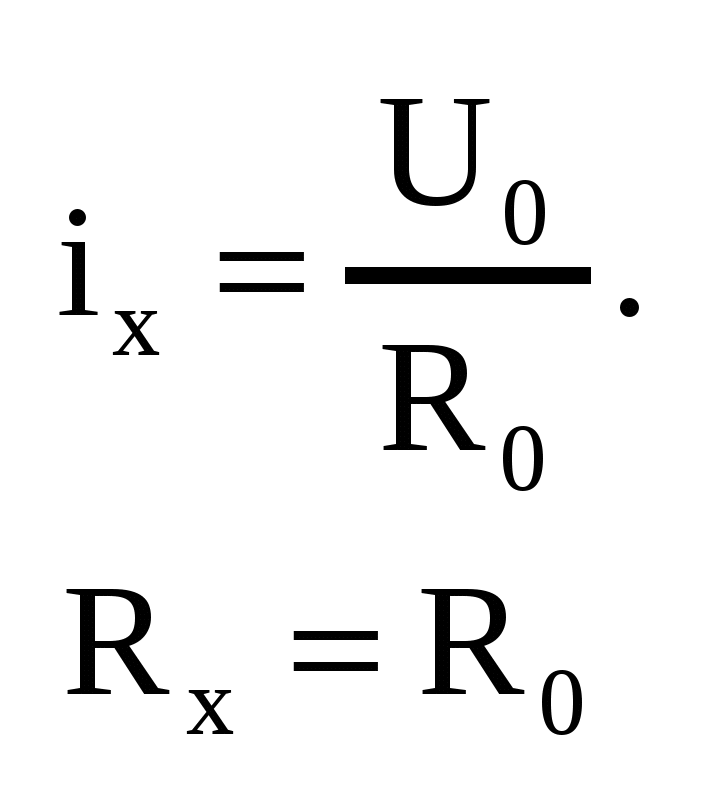 (по закону Кирхгофа) (по закону Кирхгофа)
|
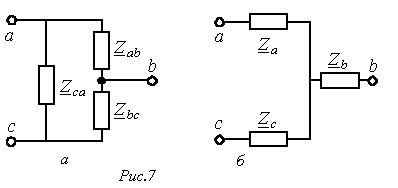
8. Преобразование соединений звездой в соединение треугольником и обратное преобразование.
Соединение 3-х сопротивлений, имеющие вид трелучевой звезды называется соединением ЗВЕЗДА, а соединение 3-х сопротивлений так, что они образуют собой стороны треугольника – соединением ТРЕУГОЛЬНИК. Если преобразование выполнить так, что при одинаковых значениях потенциалов одноименных точек треугольника и звезды подтекающие к этим точкам токи одинаковы, то вся внешняя схема не заметит замены.
Преобразовать треугольник в звезду – значит заменить три сопротивления, соединенных в треугольник между какими-то тремя узлами, другими тремя сопротивлениями, соединенными в звезду между теми же точками. При этом на участках схемы, не затронутых этими преобразованиями, токи должны остаться неизменными.
|
9. Теорема замещения.
После вычисления тока и напряжения какой-либо ветви, для вычисления токов (напряжений) остальных ветвей полезно использовать теорему замещения. Любая ветвь цепи с током ik и напряжением uk для расчетных целей может быть заменена либо на ИТ с током ik , либо ИН с напряжением uk, при этом режим останется прежним.
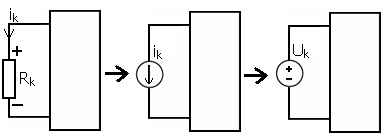
|
10. Метод узловых напряжений. Особенность составления уравнений узловых напряжений при наличии ветвей с идеальными источниками напряжения.
Порядок расчета:
1. Преобразовать ИН в ИТ (если возможно)
2. Расставить узлы преобразованной цепи (каждому узлу соответствует его 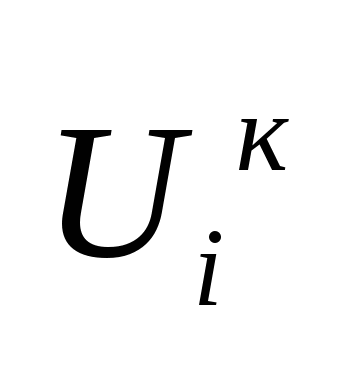 ), один из узлов принять базисным (его потенциал =0). Если остались ИН, то его «-» задает положение базисного узла, а «+» - узел, номер которого рекомендуется задавать последним. ), один из узлов принять базисным (его потенциал =0). Если остались ИН, то его «-» задает положение базисного узла, а «+» - узел, номер которого рекомендуется задавать последним.
3. Составить систему независимых уравнений:
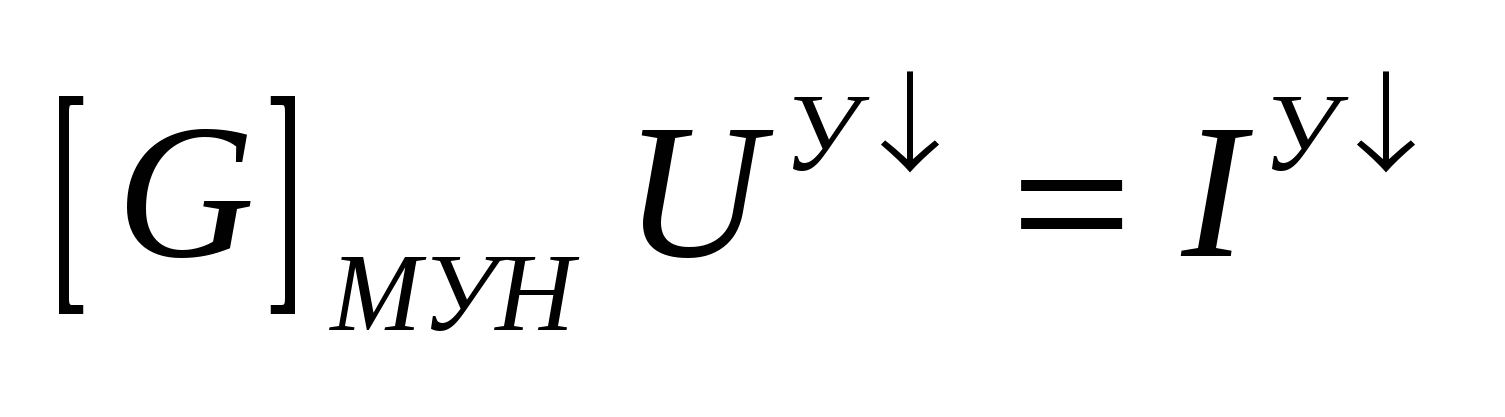 . .
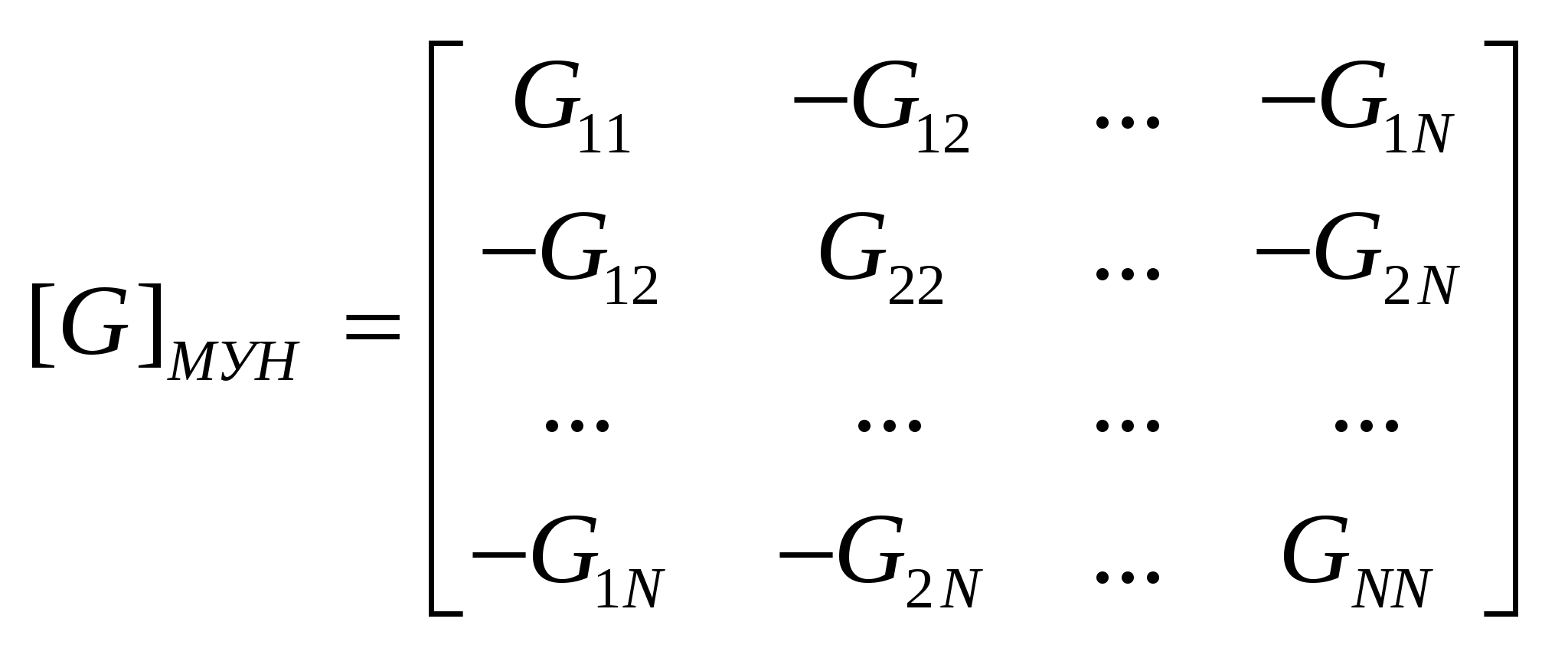 , где , где 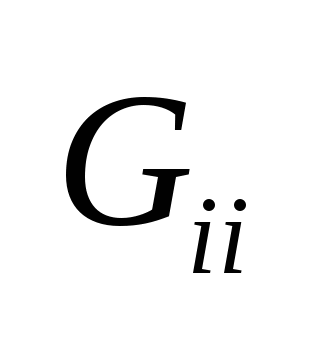 - собственная проводимость i-того узла, а - собственная проводимость i-того узла, а 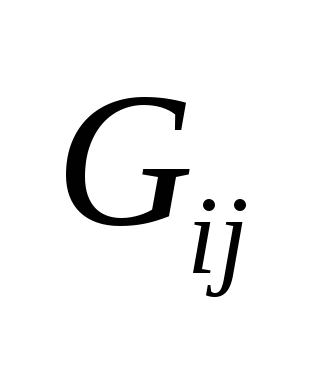 - взаимная проводимость i-того и j-того узлов (всегда «-»). - взаимная проводимость i-того и j-того узлов (всегда «-»).
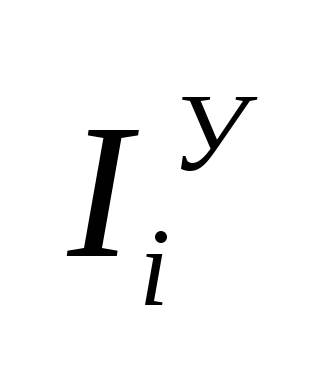 - сумма источников токов, относящихся у i-тому узлу (исход – «-», а вход – «+»). - сумма источников токов, относящихся у i-тому узлу (исход – «-», а вход – «+»).
4. Решить систему и определить напряжения (токи) цепи. 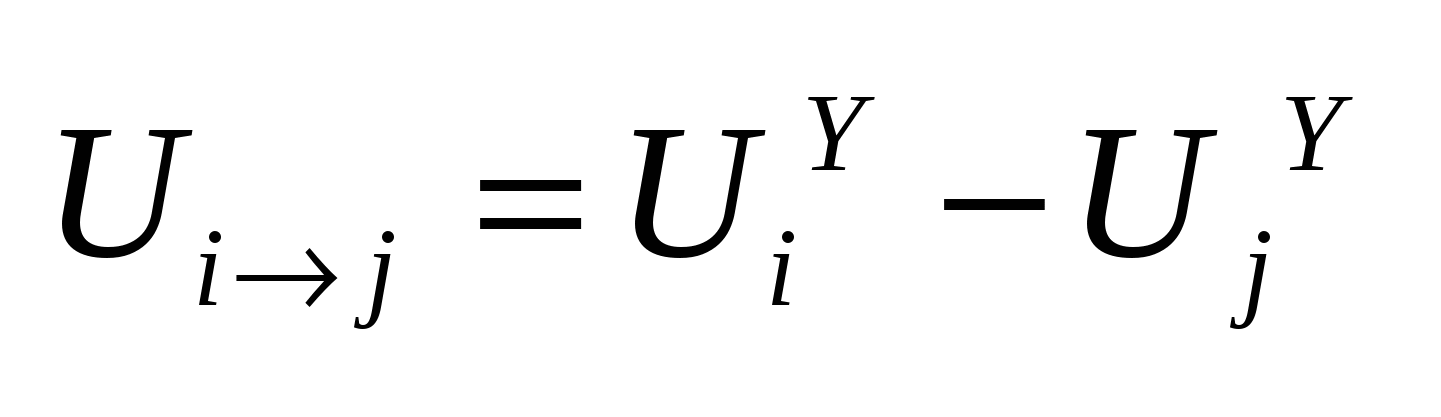 . .
5. Вернуться к исходной цепи.
|
11. Метод контурных токов. Особенность составления уравнений контурных токов при наличии ветвей с идеальными источниками тока.
Порядок расчета:
1. Выбрать направления и задать номера контурных токов. Если есть ИТ, то номер контурного тока, проходящего через ИТ, рекомендуется задавать последним. Через ИТ должен проходить только один контурный ток!
2. Составить систему независимых уравнений:
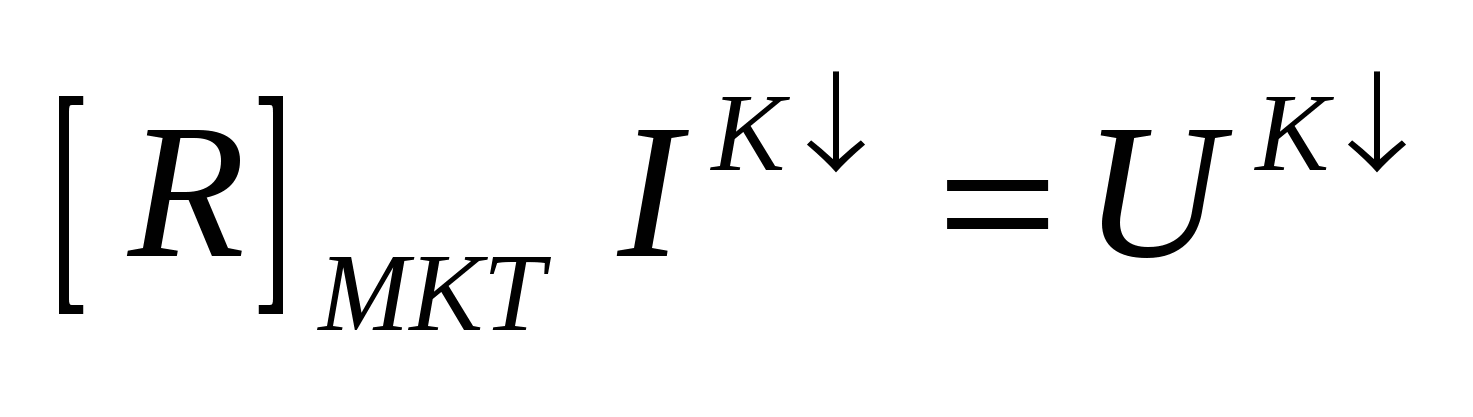 . .
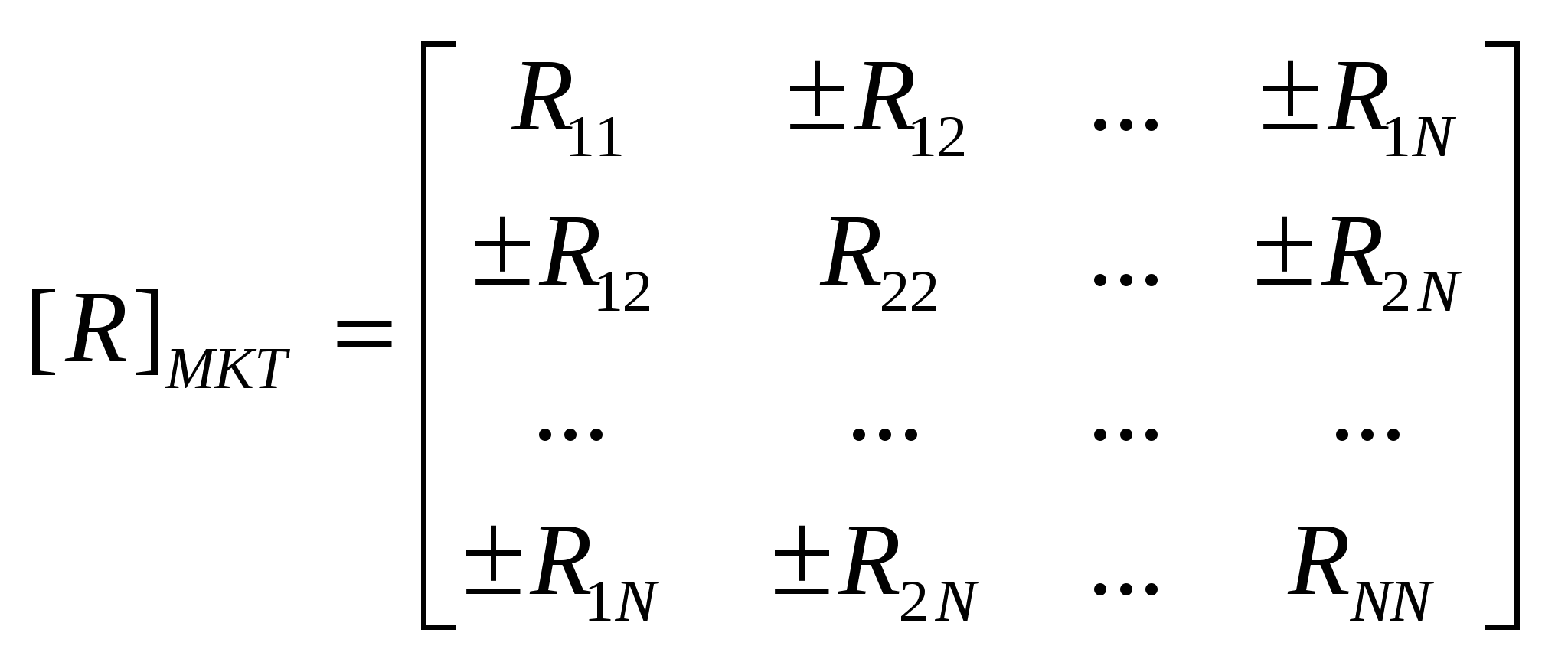 , где , где 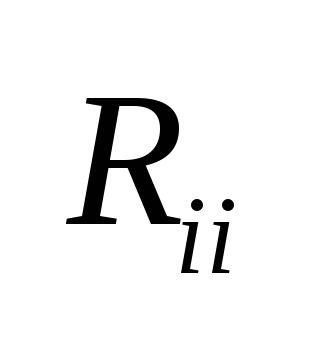 - собственное сопротивление i-того контура, а - собственное сопротивление i-того контура, а 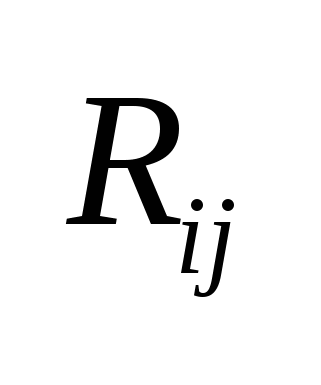 - взаимное сопротивление i-того и j-того контуров («+», если - взаимное сопротивление i-того и j-того контуров («+», если 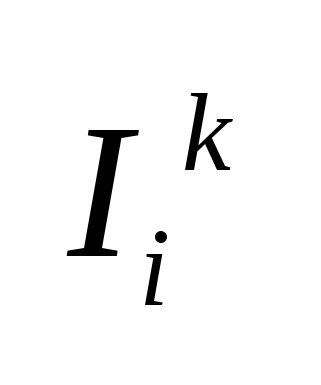 и и 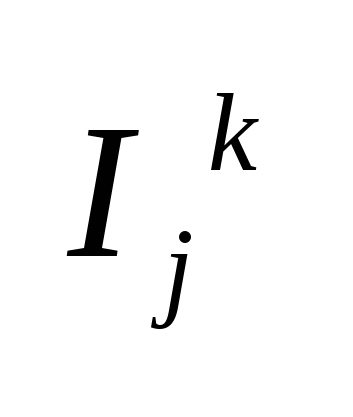 сонаправлены и «-» - в противном случае) сонаправлены и «-» - в противном случае)
 - сумма источников напряжений, относящихся у i-тому узлу (если по направлению обхода «-», то «+», в противном случае – «-»). - сумма источников напряжений, относящихся у i-тому узлу (если по направлению обхода «-», то «+», в противном случае – «-»).
3. Решить систему и определить напряжения (токи) цепи. 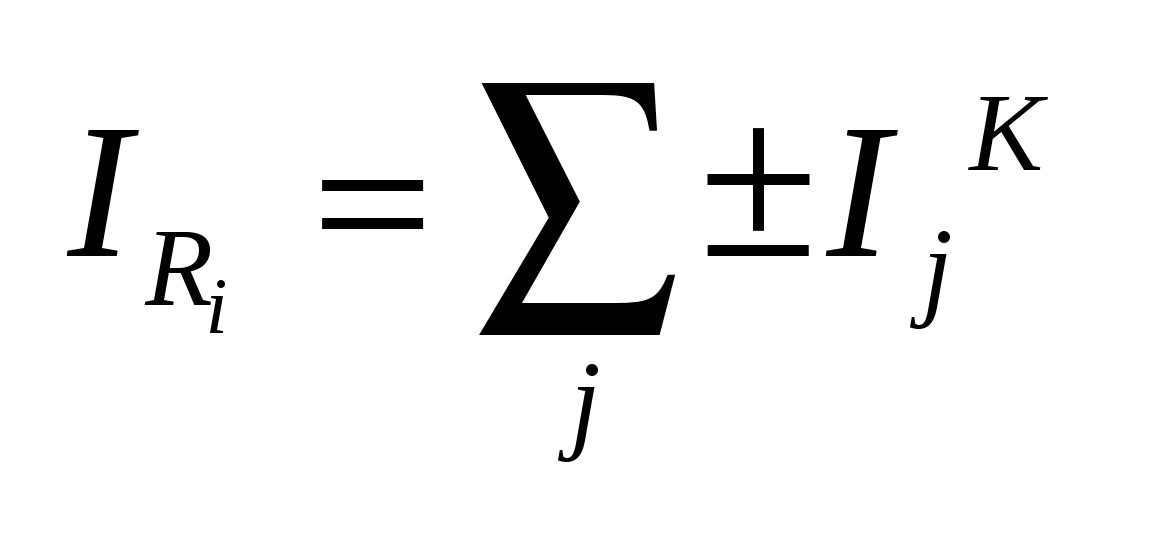 . .
|
12. Теоремы об эквивалентных источниках; теоремы Тевенена и Нортона.
Теорема Тевенена (об эквивалентном источнике): Любую активную цепь с двумя полюсами (зажимами) в установившемся режиме можно заменить источником напряжения и последовательно включенным сопротивлением.
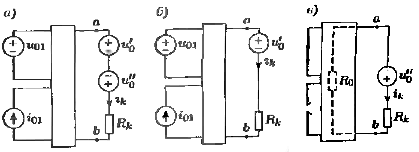
В цепи (рис б) требуется найти ток ik в одной из ветвей с сопротивлением Rk, причём источники вынесены наружу. Заменим всю цепь, по отношению к двухполюснику Rk, одним источником напряжения u0 и последовательно включенным сопротивлением R0 так, чтобы режим работы Rk не изменился (рис в). Если замена возможна, то 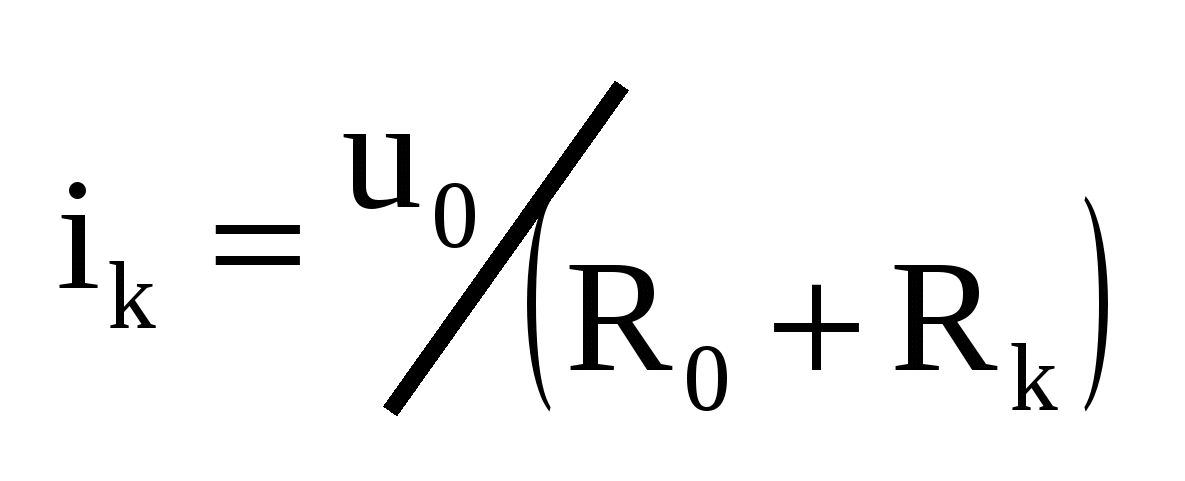 , а u0 и R0 образуют эквивалентный источник напряжения. , а u0 и R0 образуют эквивалентный источник напряжения.
Док-во: (рис а) 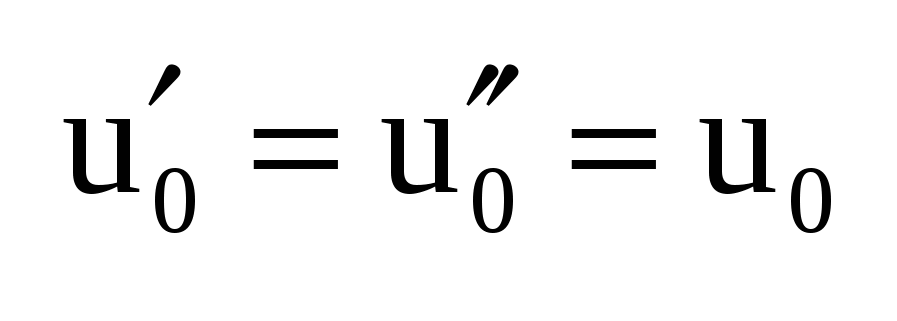 , , 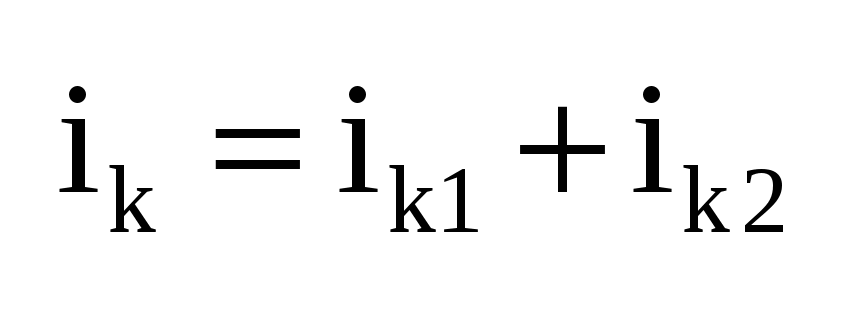 , где ik1 – ток, обусловленный действием всех источников цепи и источником , где ik1 – ток, обусловленный действием всех источников цепи и источником 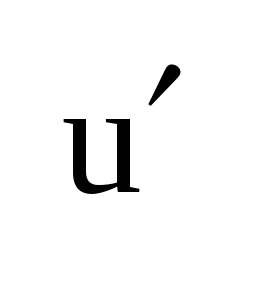 (рис б), а ik2 – ток, вызываемый действием только (рис б), а ik2 – ток, вызываемый действием только 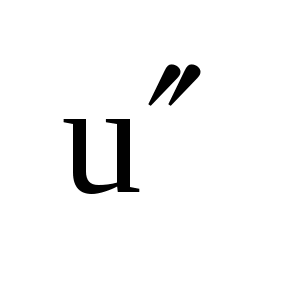 (рис в). Для цепи (рис б) ток (рис в). Для цепи (рис б) ток 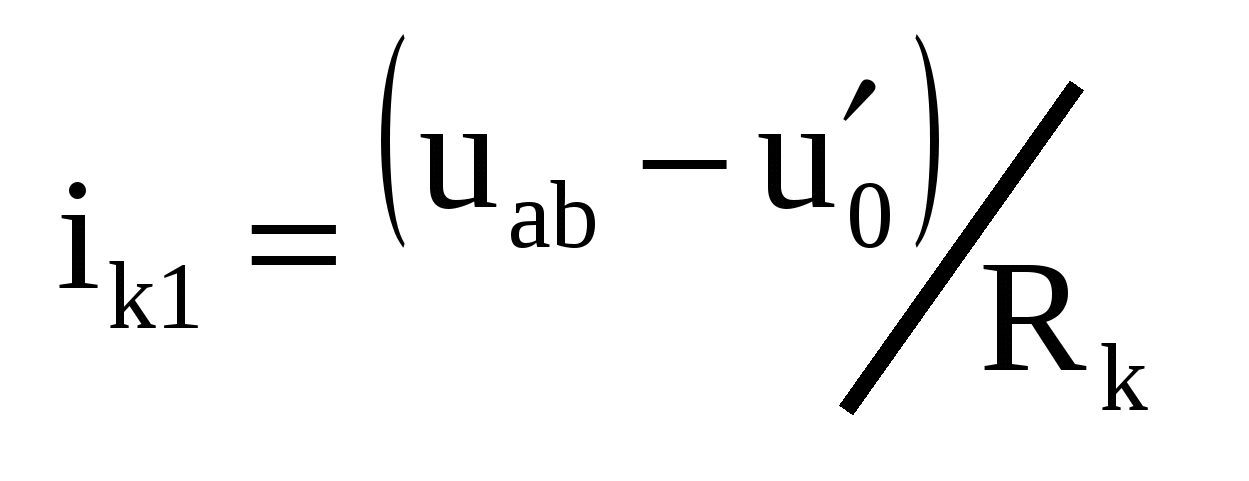 , пусть , пусть 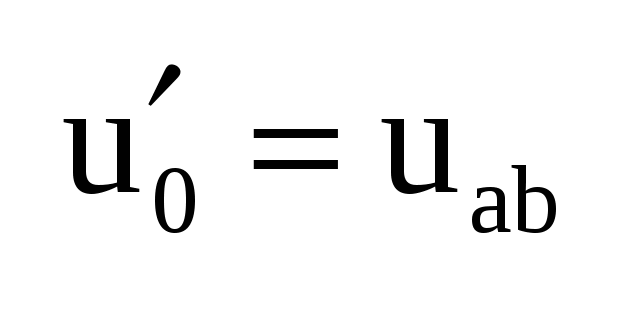 , тогда , тогда 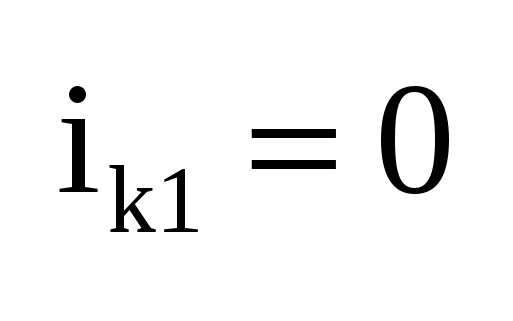 и ветвь ab можно развернуть, и тогда очевидно, что и ветвь ab можно развернуть, и тогда очевидно, что 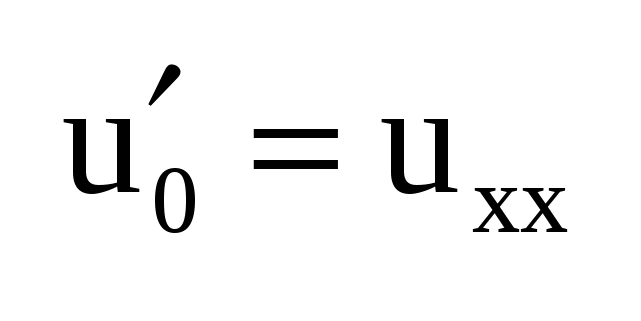 , тогда , тогда 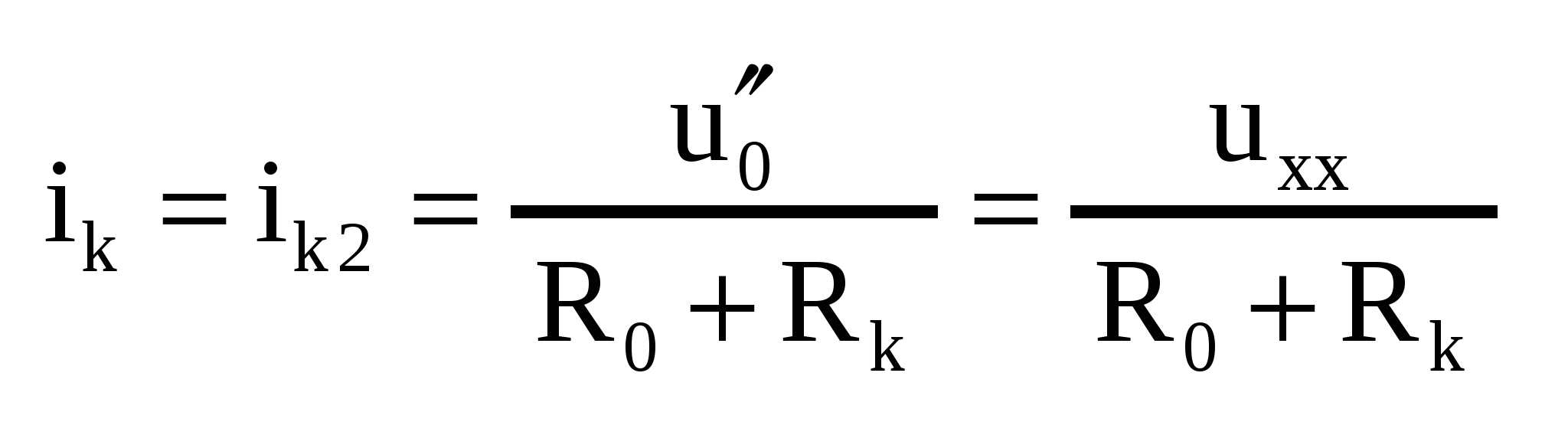 , где R0 – сопротивление полюсов относительно ab при закороченных ИН и разомкнутых ИТ. , где R0 – сопротивление полюсов относительно ab при закороченных ИН и разомкнутых ИТ.
Теорема Нортона. Любой активный двухполюсник можно заменить эквивалентным источником тока с некоторой внутренней проводимостью. (эта теорема дуальна к прошлой, доказывается аналогично)
|
13. Теорема взаимности.
Пользуясь метолом контурных токов, установим еще одно важное свойство линейных электрических цепей — свойство взаимности, или, как его еще называют, принцип взаимности.
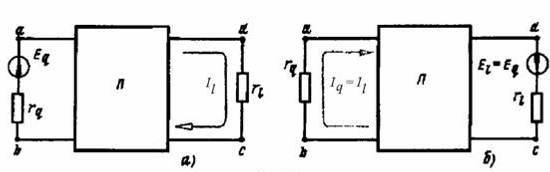
В схеме произвольной конфигурации единственный источник ЭДС Еq действует в ветви с сопротивлением rq в направлении от точки b к точке a (рис. а) и создает в ветви с сопротивлением rl ток Il направленный от точки d к точке с.
Т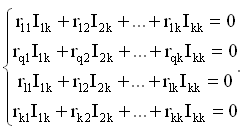 акой же единственный источник ЭДС Еl=Еq, включенный в ветвь с сопротивлением rl и действующий в направлении от d к с (рис. б), создаст в ветви с сопротивлением rq ток Iq, направленный от b к a и равный току Il. акой же единственный источник ЭДС Еl=Еq, включенный в ветвь с сопротивлением rl и действующий в направлении от d к с (рис. б), создаст в ветви с сопротивлением rq ток Iq, направленный от b к a и равный току Il.
Здесь ветвь cd является частью контура l, а ветвь ab входит в состав другого контура q (рис. а), и, как указано, других источников, кроме источника ЭДС Еq, эта цепь не содержит. Контуры выбраны так, чтобы ab и cd вошли каждая в один контур, соответственно q и l. Ток в контуре l, равный току ветви dc,
D(K) - определитель системы уравнений, Dlq - его алгебраическое дополнение, которое получается вычеркиванием из D(K) 1-го столбца и q-й строки и умножением полученного определителя на (-1)l+q. Если источник ЭДС Еq переставить в ветвь cd контура l (рис. 5.3, б) то в правой части системы (5.4) в q-й строке будет 0, а в l-й строке будет Еq. Тогда ток Iq в контуре q, т. е. ток в ветви ab,
В отличии от Dlq, алгебраическое дополнение вида Dql получается из определителя D(K) вычеркиванием столбца q и строки l и умножением получаемого определителя на (-1)l+q. Так как в контурных уравнениях общие сопротивления rlq, и rql равны друг другу, то и Dlq=Dql. Следовательно, при равенстве ЭДС Еl=Еq токи в ветвях cd (рис. а) и ab (рис. б) равны друг другу.
Свойство взаимности справедливо не только для токов, но и для напряжений.
| | |
|
|
 Скачать 4.69 Mb.
Скачать 4.69 Mb.