1. Понятие о токе, напряжении, мощности, энергии
 Скачать 4.69 Mb. Скачать 4.69 Mb.
|
|
13. Первый и второй законы коммутации в электрических цепях. Закон коммутации для индуктивного элемента: Закон коммутации для емкостного элемента: При | 14. Свободный процесс в RL-контуре. Метод подкасательной для определения постоянной времени переходного процесса в электрической RC- и RL-цепи. 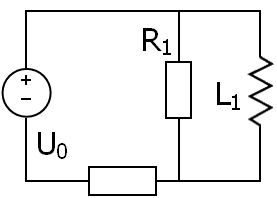 ХП (характ. полином): | 15. Включение последовательного RL-контура к источнику постоянного напряжения. Вычисление энергии, выделяемой в R-элементе при переходном процессе. 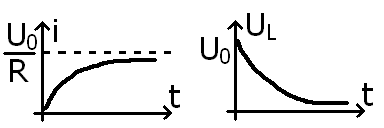 | |
| 16. Включение параллельного RC-контура к источнику постоянного тока (по принципу дуальности). 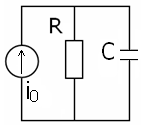 | 17. Определение порядка электрической RLC-цепи. Особый случай коммутации RC-цепи (пример анализа переходного процесса при подключении незаряженной емкости к зараженной емкости). Порядок цепи – это максимальная степень дифференциального уравнения. Во многих случаях порядок равен сумме накопительных элементов ( | 18. Анализ апериодического переходного процесса в последовательном колебательном RLC-контуре при воздействии постоянного источника напряжения. 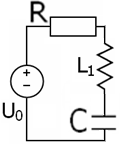 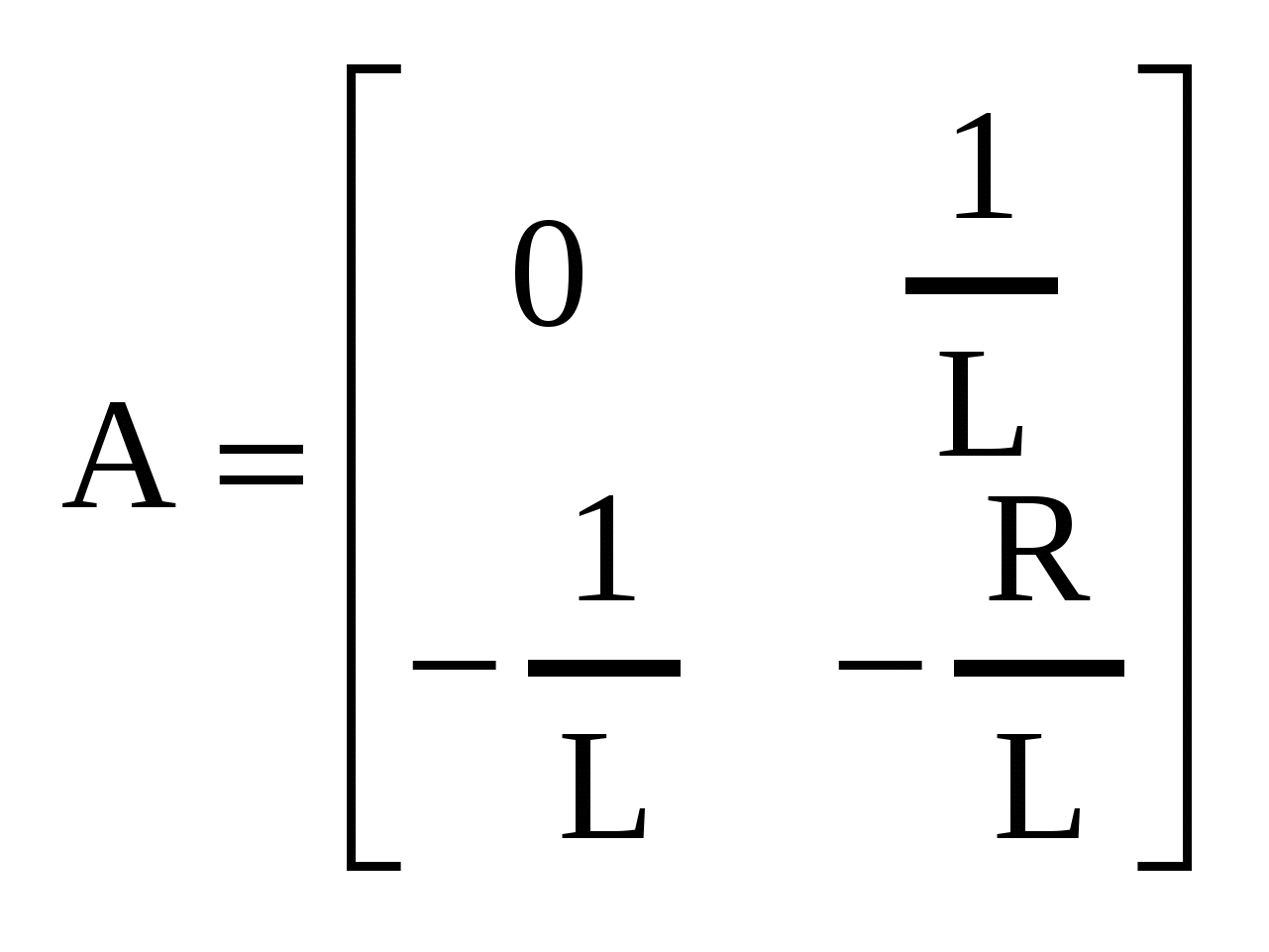 , , | 19. Анализ колебательного переходного процесса в последовательном колебательном RLC-контуре при воздействии постоянного источника напряжения. Колебательный режим |
| 20. Анализ критического переходного процесса в последовательном колебательном RLC-контуре при воздействии постоянного источника напряжения. Критический режим | 21. Составление системы дифференциальных уравнений с использованием переменных состояния. ДУ 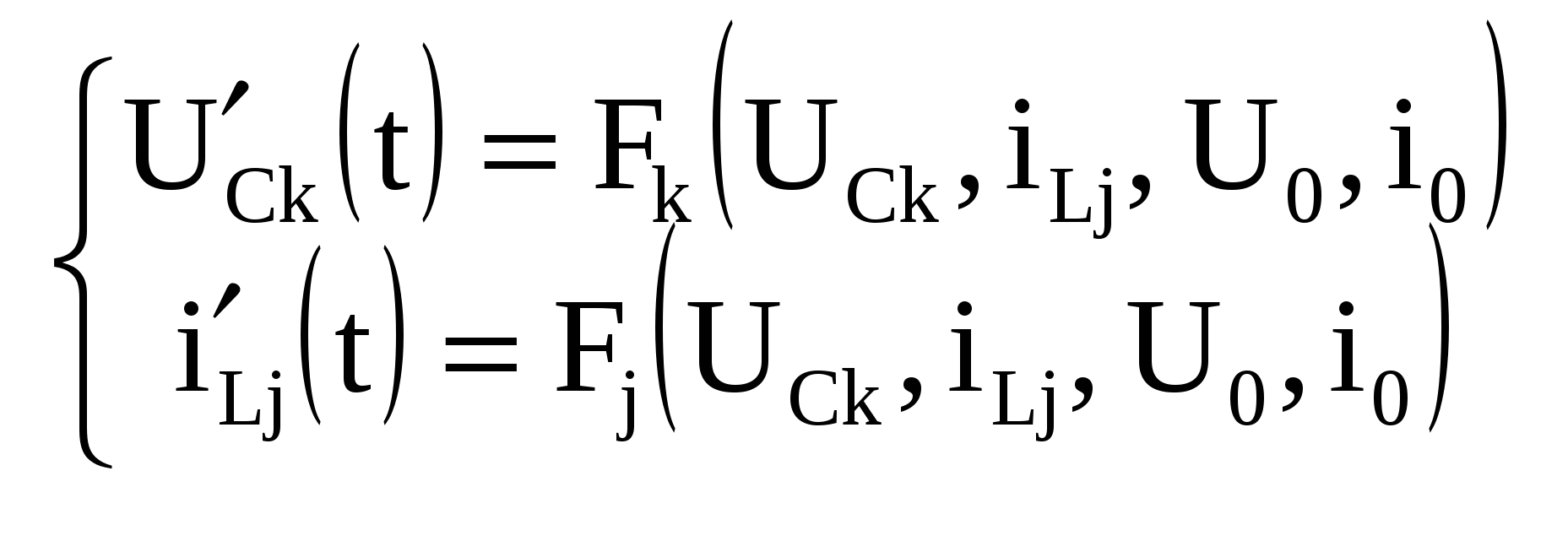 Общий вид: Вспомогательная система: 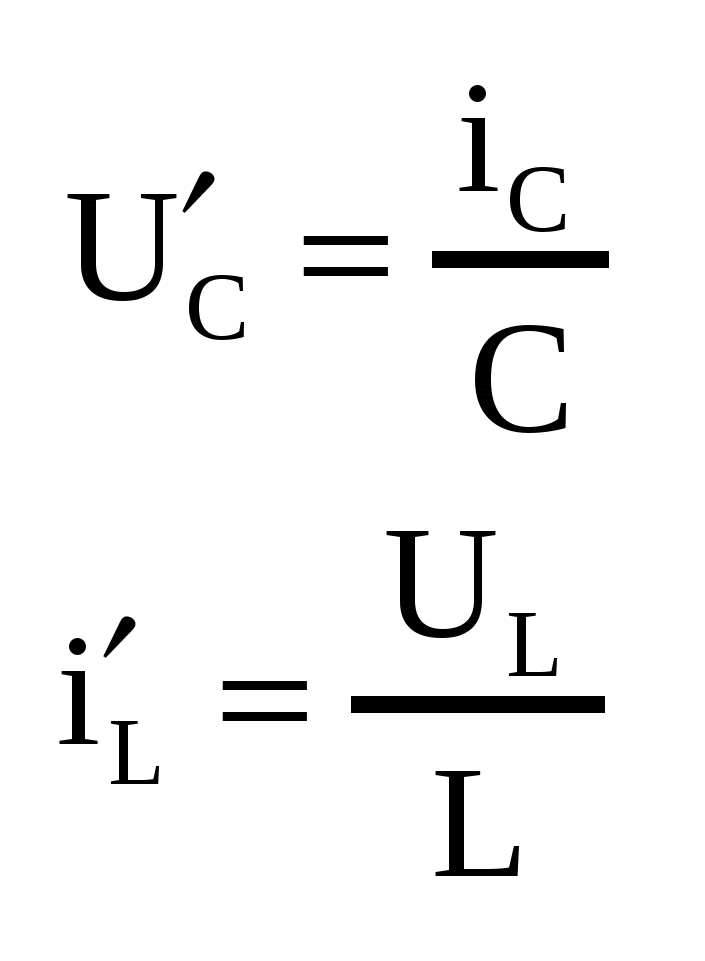 | 22. Аналитическое решение системы дифференциальных уравнений в форме переменных состояния. 1. 2. 3. 4. 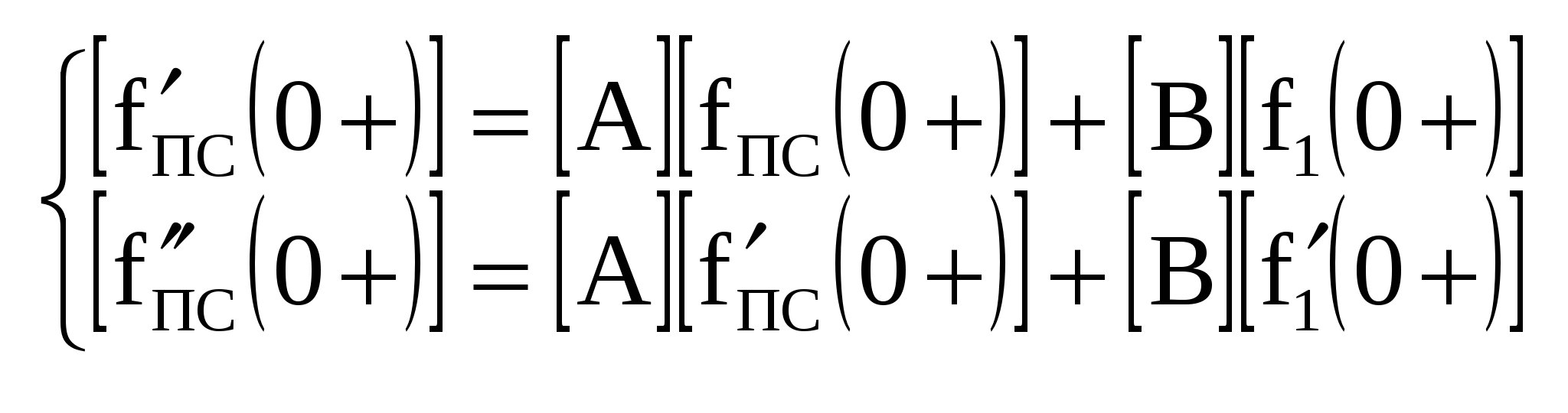 5. Ак: 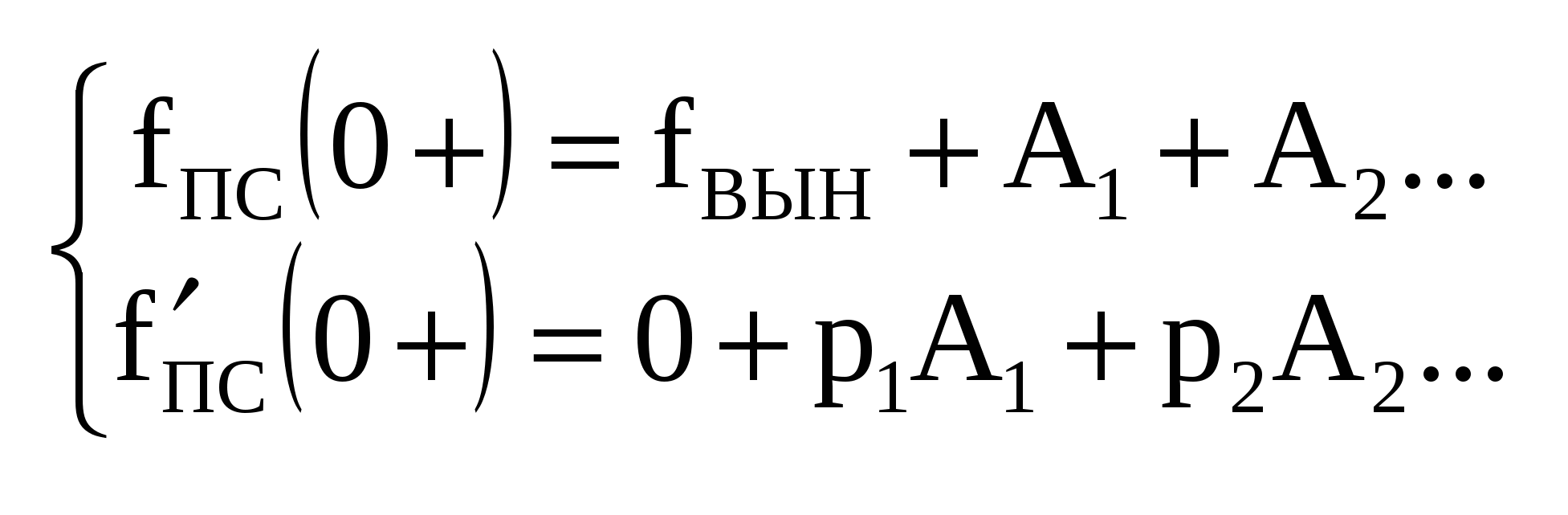 ПС - перем. состояние, СВ - своб., ВЫН – вынужд., ХП – характеристич. полином | 23. Определение единичных ступенчатой и импульсной функций. Некоторые стандартные сигналы, на которые необходимо находить отклики (из них можно выразить все остальные).
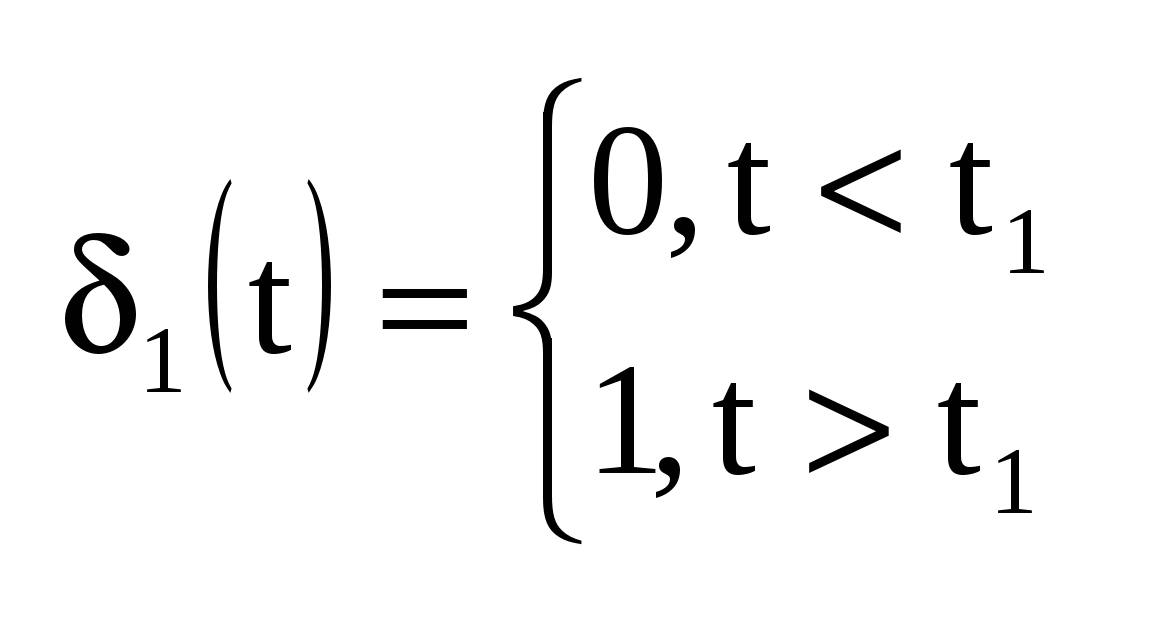 . Свойство: . Свойство: Используется для выделения функции в некотором времени.
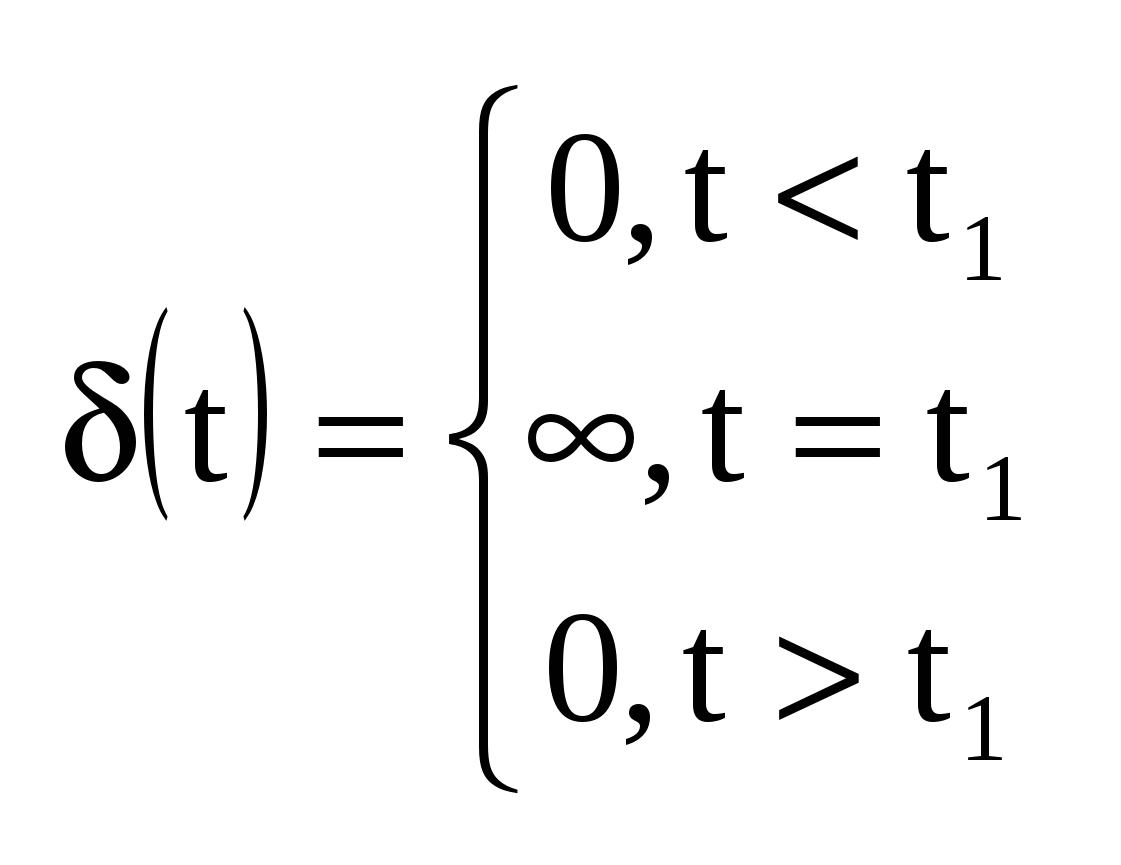 . Свойства: . Свойства:
|
| 24. Связь между единичными импульсной и ступенчатой функциями. 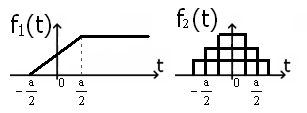 | 25. Переходная и импульсная характеристики электрической цепи. Связь между импульсной и переходной характеристиками электрической цепи. Переходная характеристика Импульсная характеристика: Характеристика | 26. Интеграл свертки (интеграл наложения, выраженный через импульсную характеристику электрической цепи). Пусть реакции, получим Интеграл свертки: | 27. Интеграл Дюамеля (интеграл наложения, выраженный через переходную характеристику электрической цепи). Пусть реакции, получим Интеграл свертки: Интеграл Дюамеля: |
| 28. Нормирование параметров элементов электрической цепи. | 29. Синусоидальные сигналы и их основные параметры. Синусоидальными сигналами или воздействиями называются переменные напряжения и токи источников, которые аналитически можно записать с помощью синусоидальной функции в синусной или косинусной форме: 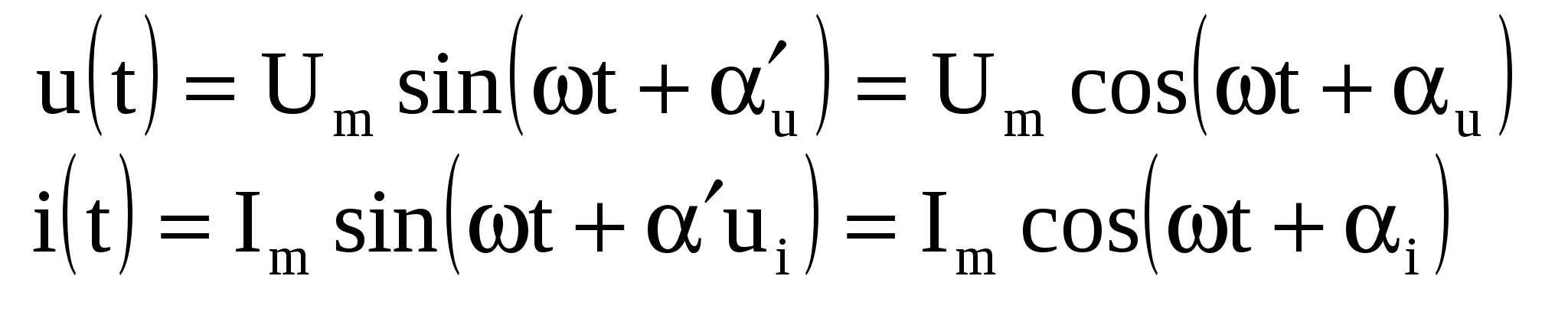 Как правило, в теории электрических цепей синусоидальные функции напряжений и токов записывают в косинусной форме, поскольку косинус функция четная и с ней проще оперировать. В записанных выражениях Um и Im амплитудные значения напряжения и тока, 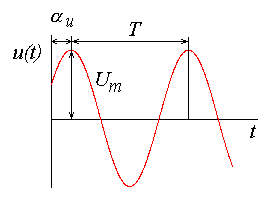 |
