1. Понятие о токе, напряжении, мощности, энергии
 Скачать 4.69 Mb.
|
|
30. Среднее и действующее значения синусоидальных токов и напряжений. Среднее за период T значение определяется как  , если  - гармоническое, то  . Средневыпрямленное значение – среднее значение положительной полуволны.  . Действительное значение периодического тока – такое значение постоянного тока, которое за время, равное периоду, выделит в R равное количество энергии. В общем случае:  , если  , то  | 31. Метод комплексных амплитуд. Законы Кирхгофа в комплексной форме. Формы записи комплексного числа: 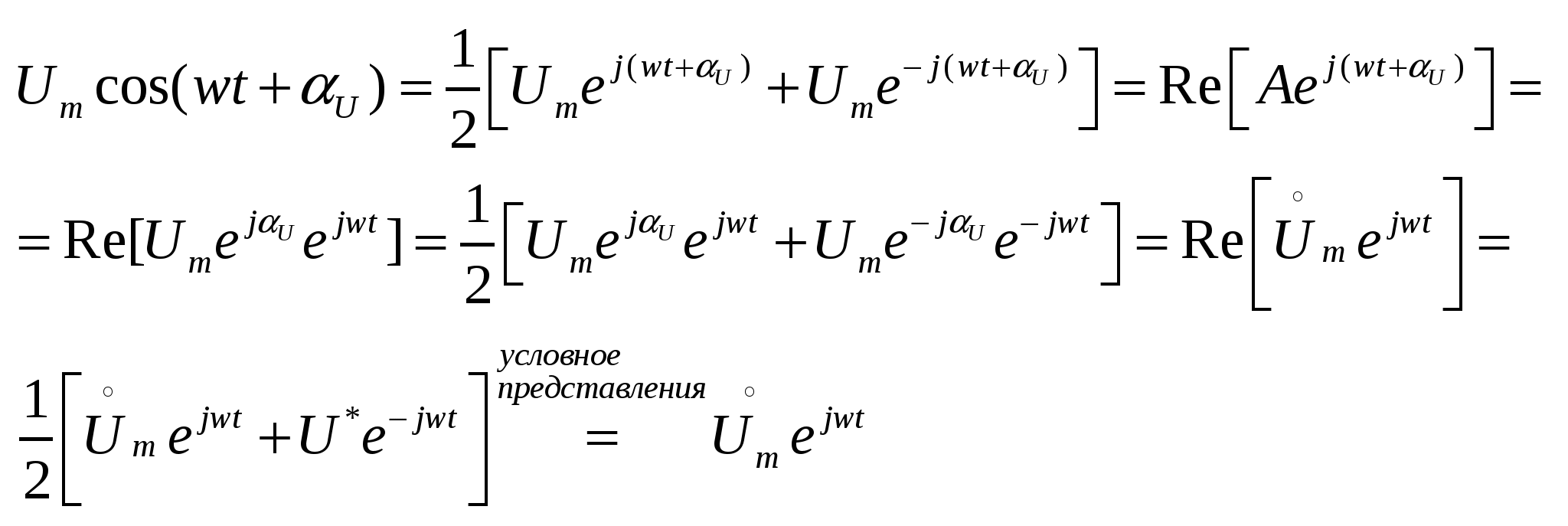 , - сопряженное. Сумма  : , если  ,то  , т.е.  Закон токов Кирхгофа:  , тогда  Закон напряжения Кирхгофа: Проводя аналогичные рассуждения  . Введем понятие комплексного R:  , где  - активное, а  - реактивное сопротивления. | ||
| 32. Характеристики резистивного элемента при установившемся синусоидальном режиме. R-элемент и его схема замещения в комплексной форме. Для определения комплексного сопротивления и комплексной проводимости R-элемента выразим синусоидальный ток, условно протекающий в нем через напряжение и сопротивление, руководствуясь при этом вольт-амперной характеристикой R-элемента:  ,  из полученного равенства можно получить выражение для комплексного сопротивления резистора: 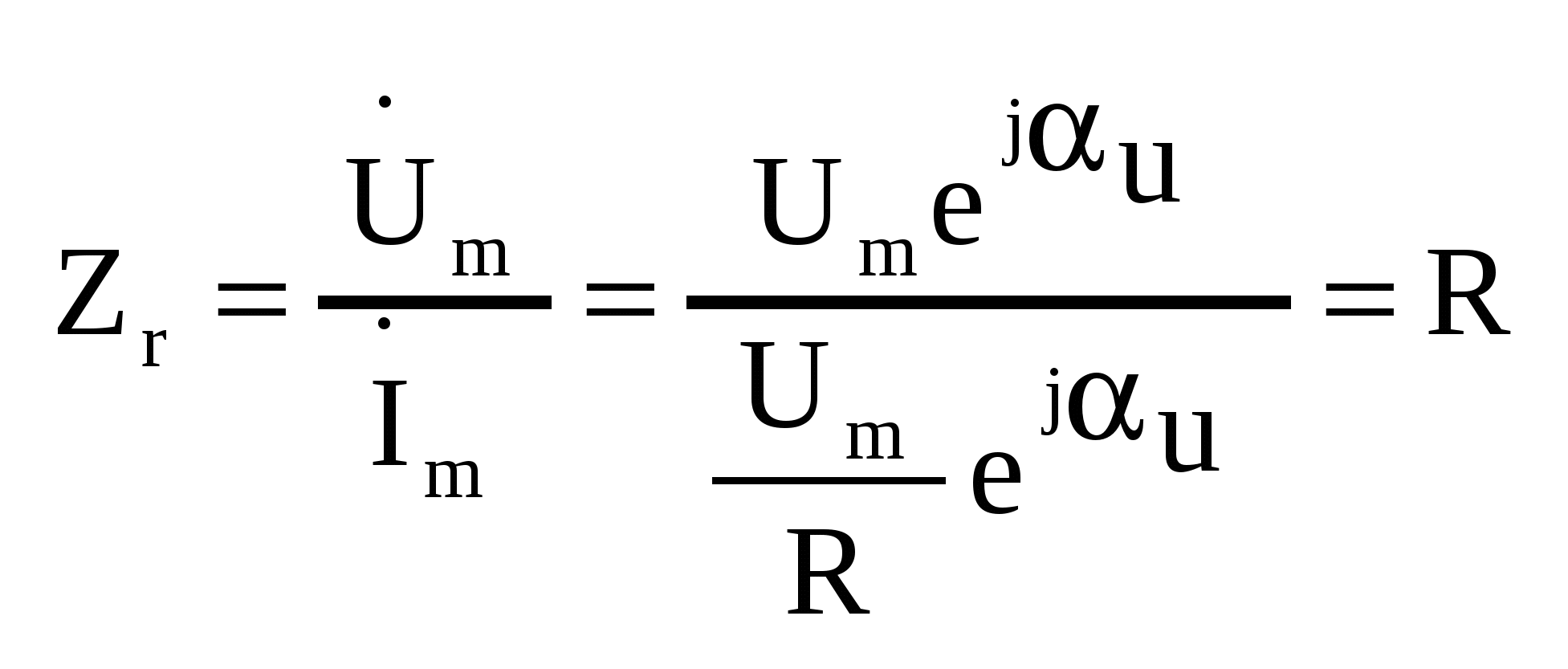 ,  ,  ,  ,  Из записанных выражений можно сделать вывод: в R-элементе ток и напряжения совпадают по фазе. Аналогично можно получить выражение для комплексной проводимости:  ,  ,  .Мгновенная мощность R-элемента определяется произведением тока на напряжения, или: 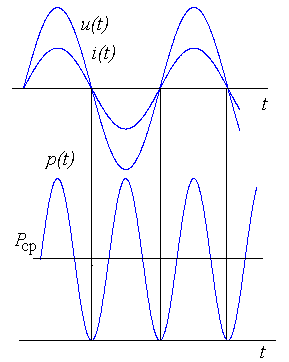  | 33. Характеристики индуктивного элемента при установившемся синусоидальном режиме. L-элемент и его схема замещения в частотной (комплексной) области Для определения комплексного сопротивления и комплексной проводимости L-элемента выразим синусоидальное напряжение на нем через ток, руководствуясь при этом вольт-амперной зависимостью L-элемента:  ,  .Разделив комплексную амплитуду напряжения на комплексную амплитуду тока можно получить выражение для комплексного сопротивления L-элемента:  ,  ,  .Из записанных выражений можно сделать вывод: в L-элементе ток отстает от напряжения на угол 900. Аналогично можно получить выражение для комплексной проводимости:  ,  ,  Мгновенная мощность L-элемента определяется произведением тока на напряжения, или:  Временные диаграммы напряжения, тока, мощности и энергии L-элемента 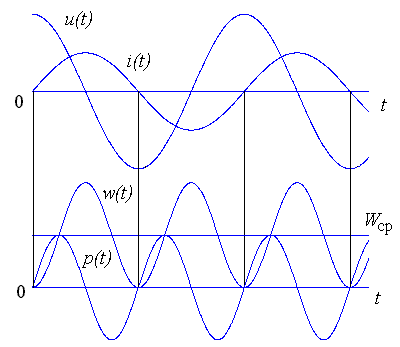 Мгновенная энергия определяется из выражения:  | 34. Характеристики емкостного элемента при установившемся синусоидальном режиме. C-элемент и его схема замещения в частотной (комплексной) области. Для определения комплексного сопротивления и комплексной проводимости C-элемента выразим синусоидальное напряжение на нем через ток исходя из его вольт-амперной характеристики:  ,  .Из записанных равенств можно получить выражение для комплексного сопротивления C-элемента:  ,  ,  .Из записанных выражений можно сделать вывод: в C-элементе ток опережает напряжение на угол 900. Аналогично можно получить выражение для комплексной проводимости:  ,  ,  .Мгновенная мощность С-элемента определяется произведением тока на напряжения, или: 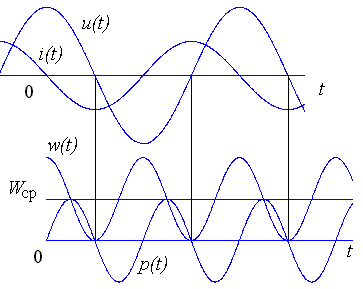  Мгновенная энергия определяется из выражения:  . | 35. Расчет индуктивного, емкостного, резонансного режимов работы в последовательном RLC-контуре. Построение потенциальной векторной диаграммы напряжений ветвей контура.  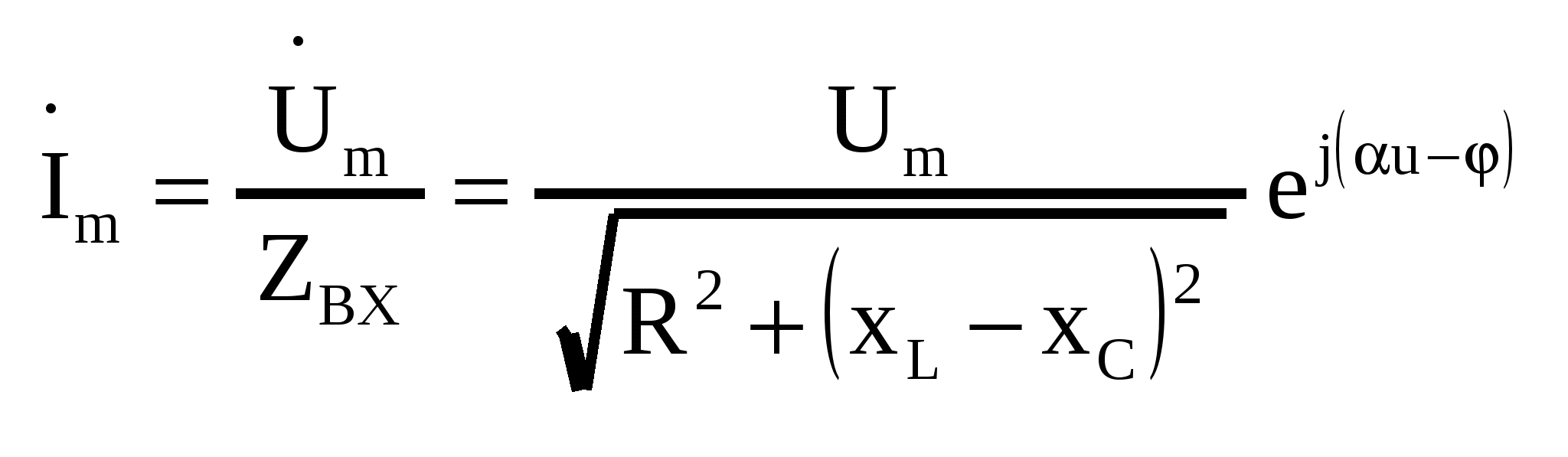 ,  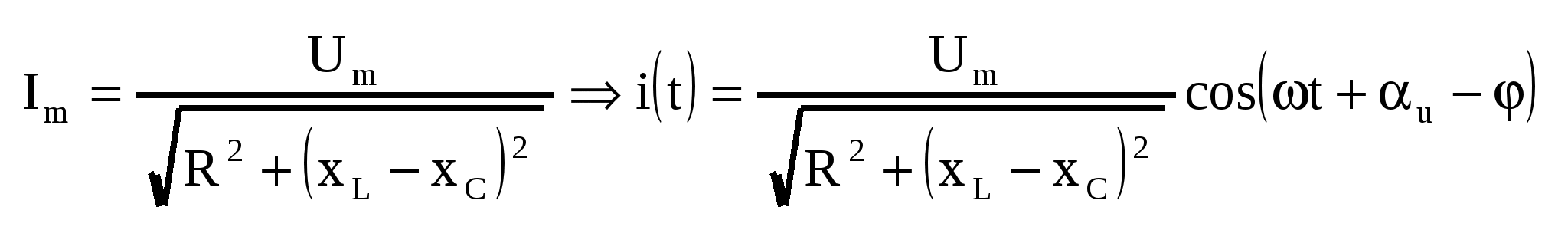,   1.  ,  ,   2.  ,  ,   3.  ,  ,   |
| 36. Расчет мгновенной мощности в двухполюснике при установившемся синусоидальном режиме. Пусть через элемент течет ток  и  ,  .  - мгновенная мощность:  .Активная мощность:  , где  Реактивная мощность:  .Активная мощность зависит от  . При   - полная мощность. | 37. Вычисление мощности двухполюсника в комплексной форме. Мгновенную мощность двухполюсника можно определить, как произведение напряжения на ток:  Это означает, что мгновенная мощность пассивного двухполюсника будет являться синусоидальной функцией с удвоенной частотой. Временные диаграммы тока, напряжения и мощности: 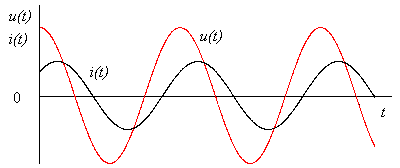 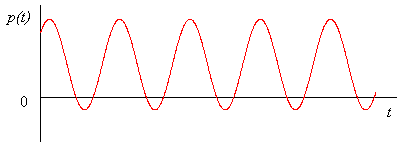 Преобразуем полученное выражение для мгновенной мощности по формулам приведения: 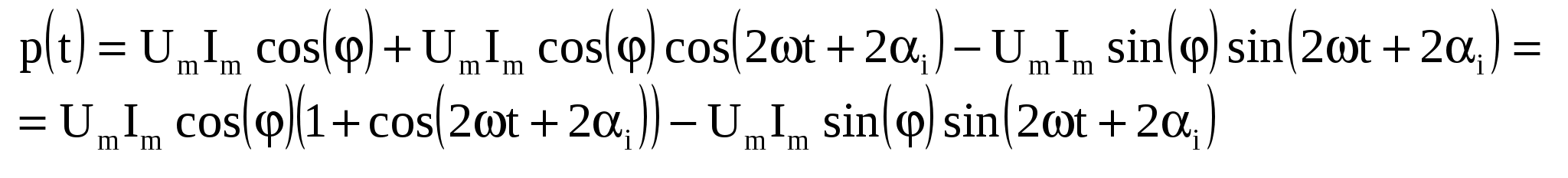 В результате проделанных преобразований мгновенную мощность удалось представить в виде суммы двух составляющих:  , где  - активная составляющая мгновенной мощности, а  - реактивная составляющая мгновенной мощности. Среднее значение активной составляющей мгновенной мощности и амплитудное значение реактивной составляющей мгновенной мощности называются соответственно: [Вт] активная (потребляемая) мощность,  [ВАр] реактивная мощность,  [ВА] полная мощность.Мощности пассивного двухполюсника можно выразить через параметры комплексного сопротивления:  ,  ,  ,  .В комплексной форме полная мощность представляется как комплексное выражение, у которого вещественная часть представляет собой активную мощность, а мнимая часть – реактивную мощность:  | 38. Улучшение коэффициента мощности двухполюсника с помощью конденсатора. При возрастании  уменьшается PQ ( ) ,  в нагрузке с R-характером  | 39. Условие согласования генератора с нагрузкой. Условие передачи максимальной мощности от источника к нагрузке. 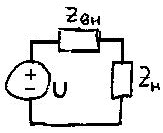 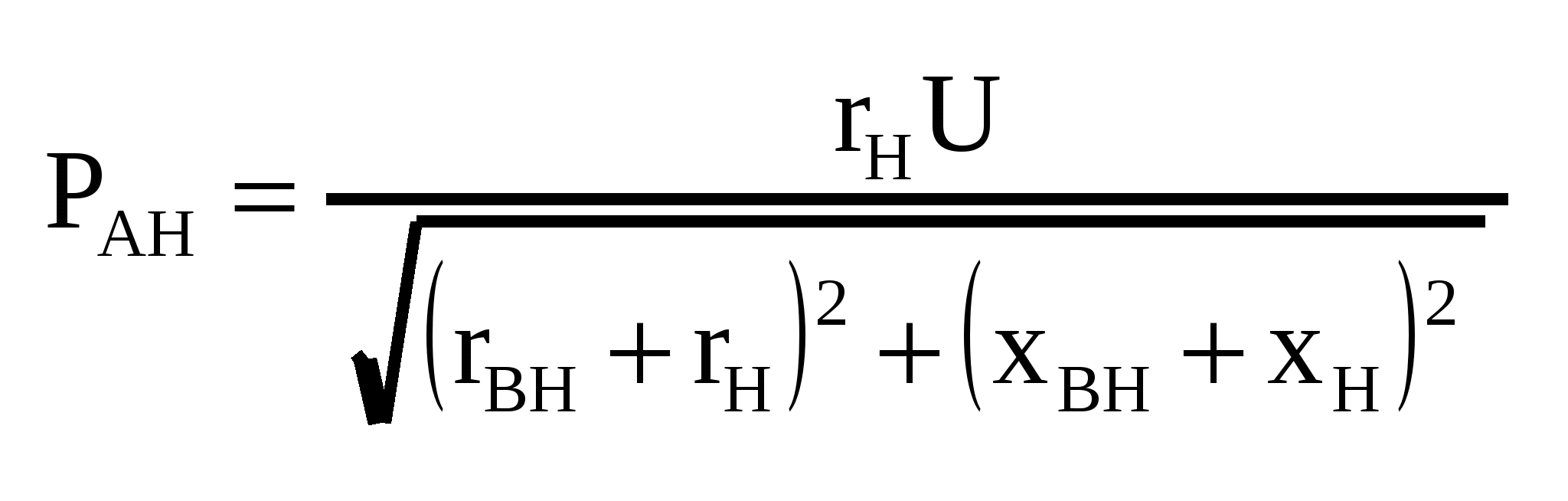 ,   ,   , для мах   ,  Кпд  |
| 4  0. Резонансные явления в электрических цепях при установившемся синусоидальном режиме.Электрическим резонансом в электрических цепях называется такое явление, при котором ток и напряжение на входе цепи в синусоидальном установившемся режиме совпадают по фазе. Такое явление можно наблюдать в том случае, если Im[ZВХ]=0 или Im[YВХ]=0. Поэтому в цепях различают резонанс в последовательном контуре (резонанс напряжений) или в параллельном контуре (резонанс токов). Резонанс в последовательном колебательном контуре. В момент резонанса мнимая часть комплексного сопротивления в таком контуре равна нулю Im[Z]=0.  , отсюда:  ,  , резонансная частота контура  .Сопротивления реактивных элементов колебательного контура зависят от частоты, следовательно, эти зависимости можно построить в функции частоты. Вертикальная линия на рисунке отмечает равенство модулей сопротивлений индуктивного и емкостного элементов, что соответствует частоте резонанса в контуре. Резонанс в параллельном колебательном контуре. Параллельный колебательный контур дуален последовательному, и все процессы в нем схожи с процессами в последовательном контуре. В  момент резонанса мнимая часть комплексной проводимости в таком контуре равна нулю Im[Y]=0.  , отсюда:  ,  , резонансная частота контура.П  роводимости реактивных элементов колебательного контура зависят от частоты, следовательно, эти зависимости можно построить в функции частоты. |