4 Интерполирование. 4 Интерполирование 1 Постановка задачи

• Название: 4 Интерполирование 1 Постановка задачи
• Дата: 04.05.2022
• Размер: 0.65 Mb.
• Имя файла: 4 Интерполирование.doc
• Тип: Документы; #512092

§4 Интерполирование
4.1 Постановка задачи
Пусть в (n+1) точках задана непрерывная функция со своими значениями , то есть фактически задана таблица




(1)

Требуется найти значение функции f для аргумента , но не совпадающего с табличным

Если аналитическое выражение функции неизвестно или очень сложное, то часто прибегают к замене функции на , которая в некотором смысле близка к функции и аналитическое выражение которой будет известно.

Записывают , где - приближающая функция.

Существуют различные способы построения приближающей функции. Это зависит от выбора критерия близости.

Классическое построение приближающей функции основывается на требовании строгом совпадения значений функции и в заданных точках, то есть ;

Нахождение функции, удовлетворяющей этим условиям, называется интерполированием или интерполяцией.

- интерполирующая функция;

- интерполируемая функция;

заданные точки - узлы интерполяции.

Будем искать интерполирующую функцию в виде многочлена степени не выше n, который в заданных точках принимает такие же значения, что и заданная функция .

( * ) – условие интерполирования, . Многочлен называется интерполяционным многочленом, само интерполирование - параболическим.

Таблица 1 задает систему точек геометрический смысл интерполяции заключается в том, что график функции заменяется параболой n –го порядка, являющийся графиком и проходящей через заданные точки , то есть график функции и имеют (n+1) общую точку.

4.2 существование и единственность интерполяционного многочлена
Интерполяционный многочлен можно записать по убывающим степеням.
(2)
Неизвестные коэффициенты многочлена будем искать из условия ( * ).

Получим систему из (n+1) уравнения с неизвестными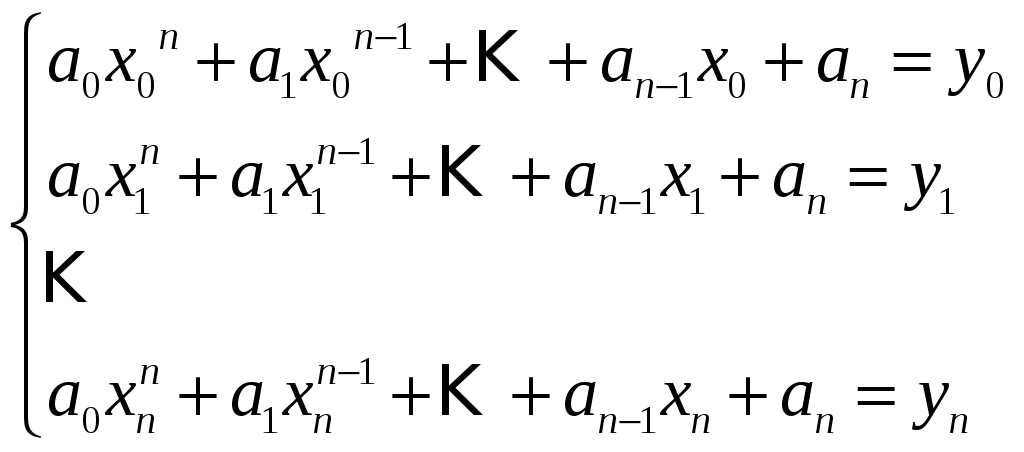
(3)
(3) – линейная неоднородная система.

Запишем определитель системы 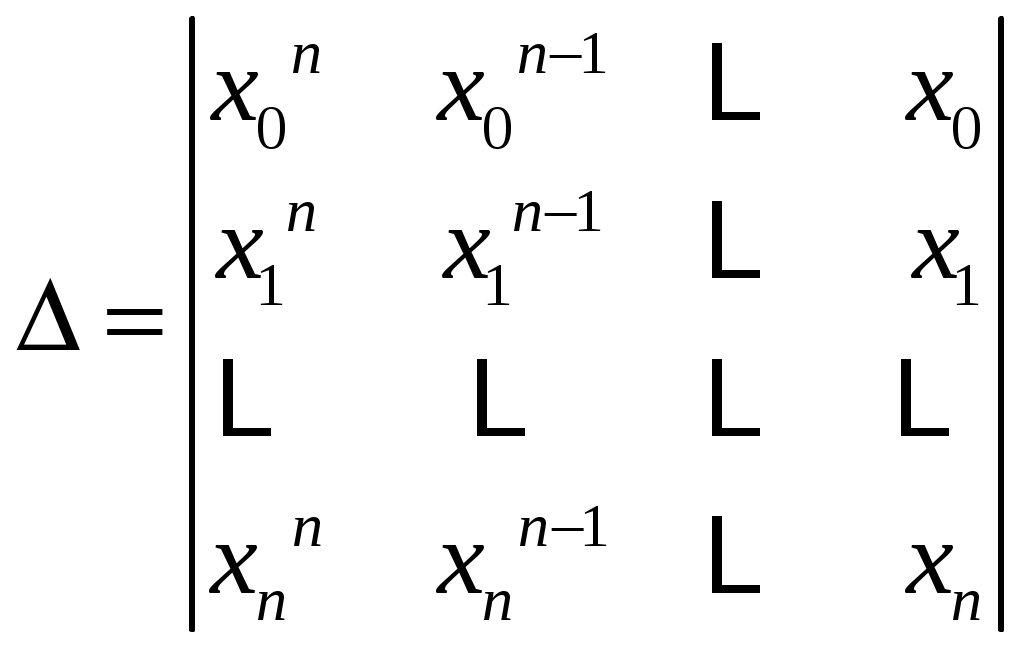, где - определитель Вандермонда,

Так как узлы интерполирования различны, то определитель система (3) имеет единственное решение, то есть коэффициенты многочлена (2) существуют и определяются единственным образом.

Замечание: решая системы с (n+1) неизвестными, то есть имея (n+1) узел интерполяции, мы получаем многочлен степени не выше n.

Такой способ отыскания коэффициентов многочлена связан с решением системы, увеличение количества узлов интерполяции приводит к большим трудоемким вычислениям. Другой способ отыскания коэффициентов был предложен Лагранжом.

4.3 интерполяционный многочлен Лагранжа
Пусть функция 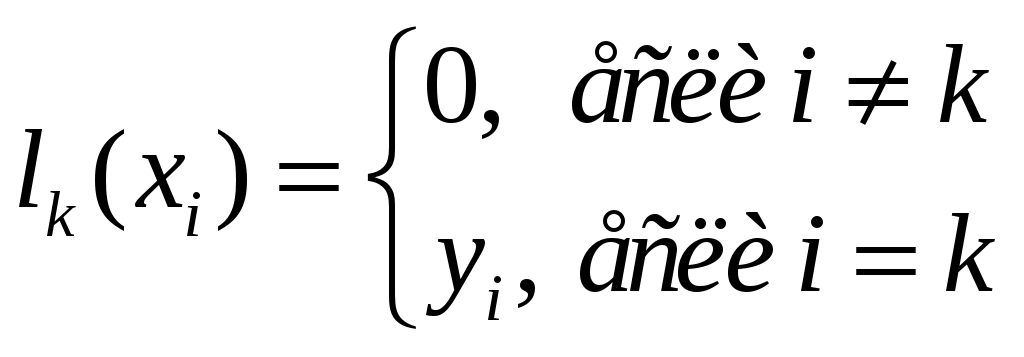задана таблицей 1, построим интерполяционный многочлен , который удовлетворял бы условию (*). Будем искать в виде
(4),
где - многочлен степени не выше n и удовлетворяет следующему условию:

(**)

Из условия (**) следует, что все узлы, кроме одного, а именно являются нулями многочлена .

(5)
А при ; ,

тогда

Подставляя в (5) получаем



Так как , то окончательно получим
(6)
Многочлен (6) и есть многочлен Лагранжа.

Многочлен (6) можно записать и в более краткой форме.

Обозначим - многочлен (n+1) степени.

Производная от точки имеет вид:


(7)
Многочлен (7) и есть краткая запись многочлена Лагранжа.

Приближенное равенство
(8)
называется интерполяционная форма Лагранжа.

Пример: построить интерполяционный многочлен Лагранжа для функции заданной таблицей.

	0	0.5	1	2
	1	2	4	3

n +1=4 – количество узлов;

n=3 - степень многочлена.



4.4 Оценка погрешности интерполяционной формулы Лагранжа

(8)
Заменяем в вычислениях значение функции значением интерполяционного многочлена в формуле (8), мы допускаем тем самым погрешность.

Обозначим разность

- остаточный член формулы Лагранжа. Он и дает погрешность метода.

Теорема: если функция 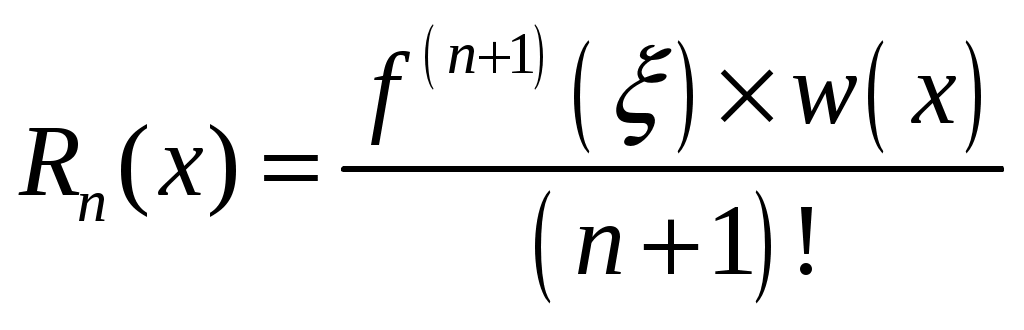имеет на непрерывную производную до (n+1) порядка , то остаточный член можно представить в виде , где .

Если будет известно, что 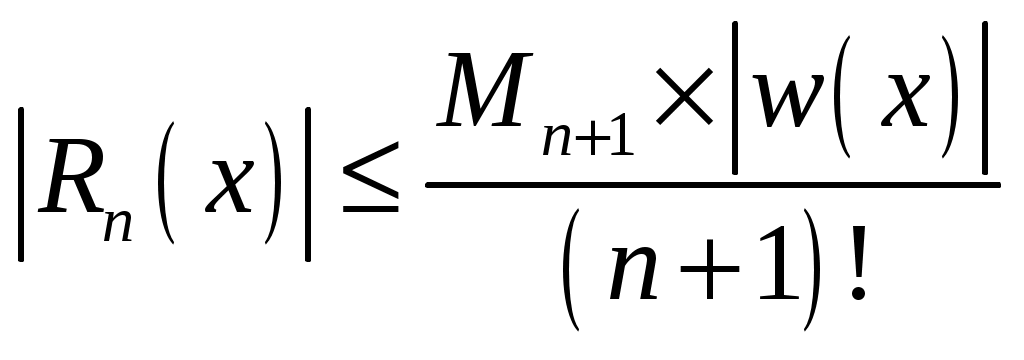, то получим оценку погрешности.
(9)
Формула (9) дает погрешность метода

Пример: С какой точностью можно вычислить 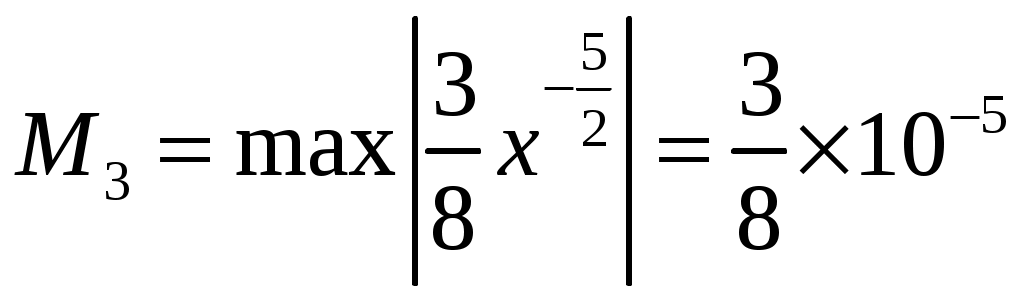, с помощью интерполяционной формулы Лагранжа построенный для функции ,используя 3 узла интерполяции.

n+1=3, n=2 – степень многочлена

За можно принять на отрезке





, на отрезке


4.5 Табличные разности (конечные разности)
Пусть функция задана в равноотстоящих узлах интерполяции. Назовем узлы интерполирования равноотстоящими, если они пронумерованы в порядке возрастания и расстояние между соседними узлами одинаковое равное h , то есть задается таблица с постоянным шагом h.



Разности между соседними табличными значениями функции называют табличными разностями 1-го порядка (первые табличные разности).











- единственное значение

Пример:

Табличные разности любого порядка могут быть выражены через значения функции:










4.6 Интерполяционный многочлен Ньютона
Пусть функция задана таблицей с постоянным шагом h, то есть

Будем искать интерполяционный многочлен в виде:
(10)
Неизвестный коэффициент найдем из (*)

При



Полагая, что при





Полагая, что при







Проведя аналогичные рассуждения, получаем:



Подставив полученные коэффициенты в ( 10 ), будем иметь
(11)
Многочлен (11) и есть интерполяционный многочлен Ньютона.

На практике многочлен Ньютона применяют в несколько ином виде.

Если обозначим , то

Многочлен (11) примет вид
(12)


Многочлен (12) и называют первый интерполяционный многочлен Ньютона.

В выражение многочлена входят табличные разности

Поэтому этот многочлен используют для интерполирования в начале таблицы, когда t мало по абсолютной величине

Замечание: если требуется вычислить значение функции для аргумента , то за выбирают ближайшее, причем меньшее табличное значение аргумента.

Пример:

1.5	3.7
1.6	3.9
1.7	4.1
1.8	4.5
1.9	5.0

Приближенное равенство

(13)

называют интерполяционной формулой Ньютона.
4.7 Погрешность интерполяционной формулы Ньютона
, заменяя в вычисленияx значение функции значением интерполяционного многочлена мы допускаем погрешность.

Обозначим

- остаточный член формулы Ньютона,он и дает погрешность метода.

В силу единственности интерполяционного многочлена 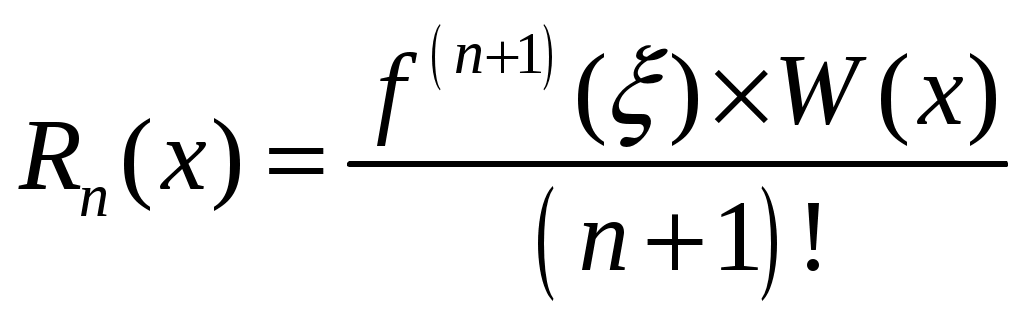и для многочлена справедливо будет

, где



Если узлы равноотстоящие, то введя замену 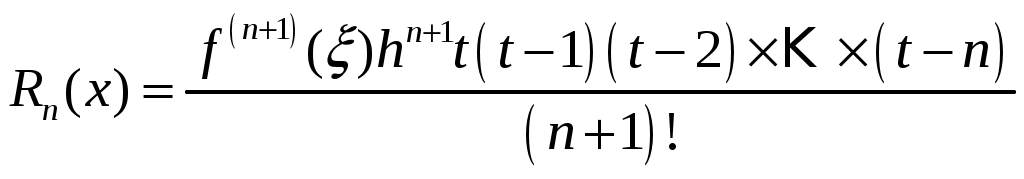, погрешность выражается формулой



Если будет известно, что , то получим оценку погрешности.
(14)
Можно принять

на

Если аналитическое выражение функции заданной таблицей, неизвестно, то используют формулу практической оценки погрешности.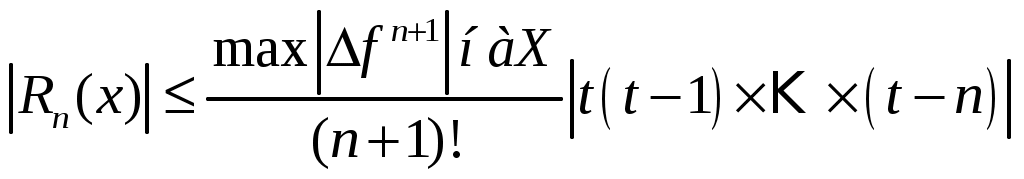
(15)
Так как при малых h и в силу непрерывности производных


4.8 Частные случаи интерполирования
1) линейное интерполирование

Имеем 2 узла интерполирования . n=1 – степень интерполяционного многочлена.

Из формулы (12) при n=1 получим , а

приближенное равенство (13) примет вид
(16)
Формула (16) и есть формула линейного интерполирования.

Геометрический смысл линейного интерполирования:
y M₁




M₀



0 x₀ x₁ x


дается 2 узла .

При линейном интерполировании дуга кривой заменяется отрезком прямой

2) квадратичное интерполирование. Имеем 3 узла интерполирования , равноотстоящие, n=2 – степень интерполяционного многочлена, тогда из (12) при n=2 получим



А интерполяционная формула примет вид
(17)
Формула (17) и есть формула квадратичного интерполирования.

Геометрический смысл: при квадратичном интерполировании дуга кривой заменяется дугой параболы, проходящей через точки


3) допуск линейного интерполирования

Определение: говорят, что таблица допускает интерполирование n-го порядка, если погрешность метода при использовании интерполяционного многочлена n-го порядка не превосходит точности табличных значений функции, то есть , где - точность значений функции.

Итак, пусть задана таблица, в которой все значения функции записаны с точностью

Воспользуемся формулой практической оценки погрешности (15) при n=1, будем иметь



Рассмотрим функцию

Исследуя ее на экстремум на , получим , тогда

Очевидно, что если вторые табличные разности не превосходят 4х единиц младшего разряда табличных значений функции, то есть , то получим

Значение функции вычислимое с помощью линейного интерполирования имеет ту же точность, что и табличные значения функции, а это значит, что таблица допускает линейное интерполирование.

Отсюда критерий:таблица или ее часть допускает линейное интерполирование, если модули вторых табличных разностей не превосходят 4х единиц младшего разряда табличных значений функций.

4) критерий допуска квадратичного интегрирования.

Пусть - точность табличных значений функции

При n=2 из (15) получим



Рассмотрим функцию , исследуя ее на экстремум на отрезке и

Тогда условие допустимости запишется

Если то значение функции, вычисленное с помощью формулы квадратичного интерполирования будет иметь ту же точность, что и значения функции в таблице, а это значит, что таблица допускает квадратичное интерполирование. Отсюда критерий: таблица или ее часть допускает квадратичное интегрирование, если модуль третьих табличных разностей не превосходит семи единиц младшего разряда значений функции


4.9 Интерполяционный многочлен Лагранжа для равноотстоящих узлов
Рассмотрим многочлен Лагранжа в краткой форме

, где - значение функции





Будем рассматривать равноотстоящие узлы с шагом h, h – шаг интерполирования, тогда





Рассмотрим дробь

Введем новую переменную

Если , то

и многочлен Лагранжа запишется в виде



Это и есть многочлен Лагранжа для равноотстоящих узлов интерполирования.