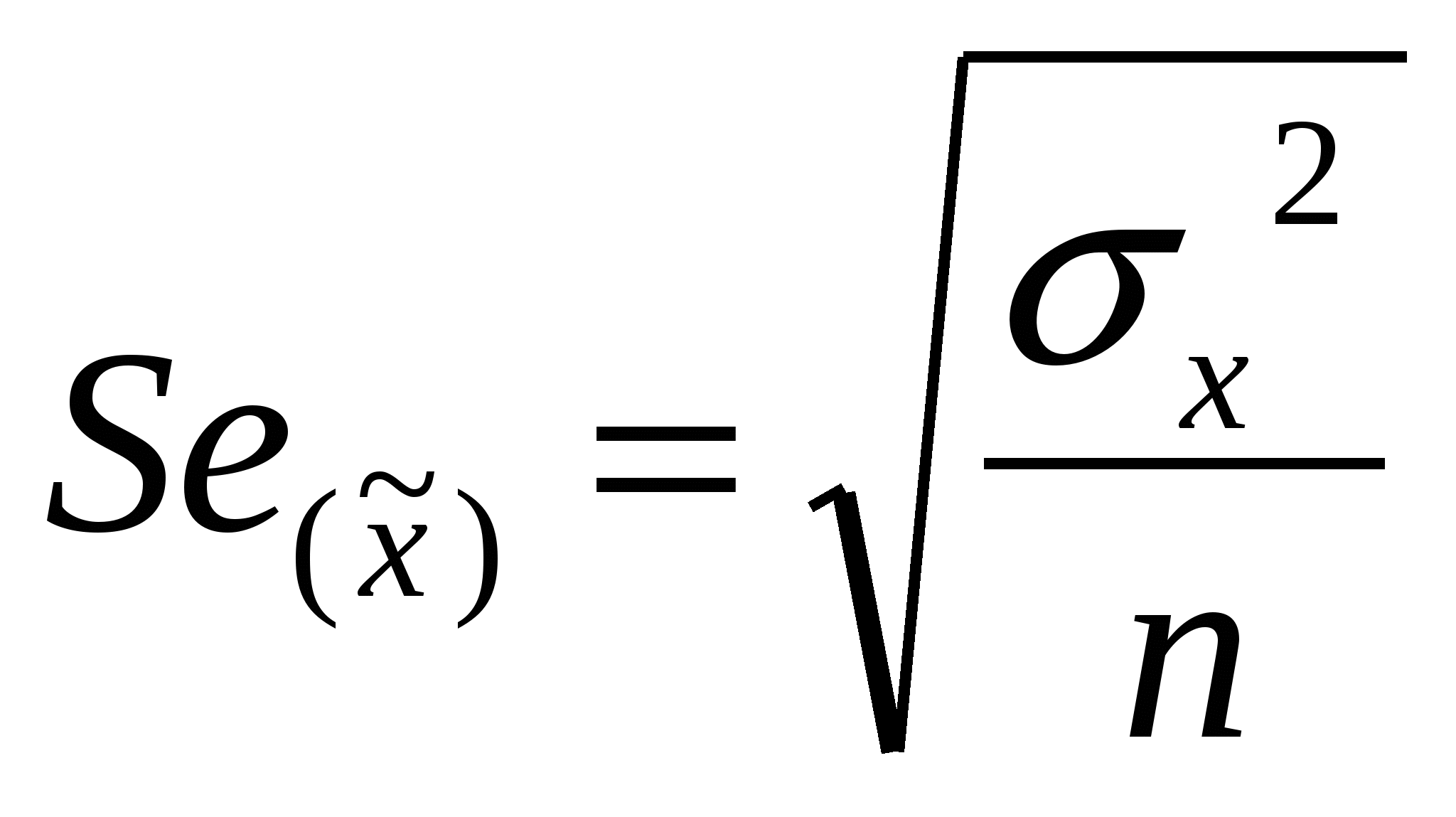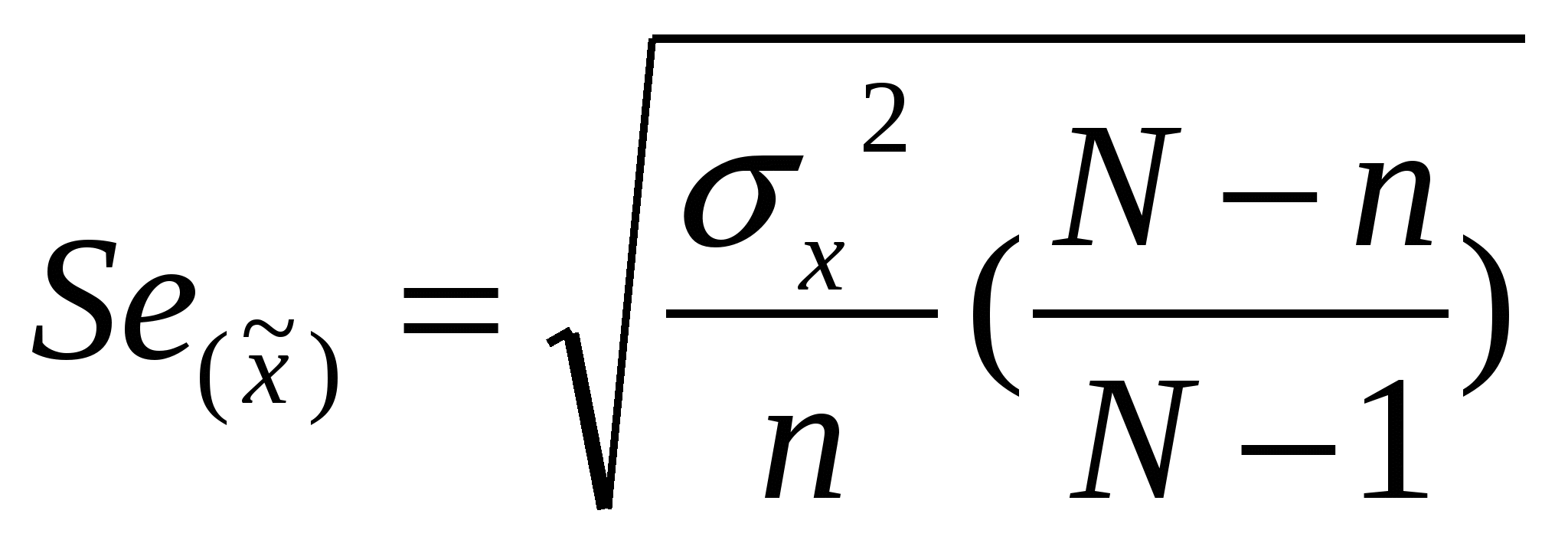Шпора по статистике. 1. Понятие об учете, виды учета. Статистический учет, его значение, задачи и особенности. Организация статистической деятельности в России
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
18. Задачи и значение статистического изучения связи. Виды связей социально-экономических явлений, основные методы их статистического изучения. Особенность связей в экономике состоит в том, что их закономерный характер проявляется лишь в массе явлений – в среднем по совокупности. Например, затраты на рекламу, способствуя продвижению товара. Приводят к увеличению выручки от продаж. Но по отношению к отдельному товару, отдельному продавцу эта закономерность может не подтвердиться. Она проявляется лишь в целом для многих товаров и фирм, и на основе обобщенных характеристик делается вывод об эффективности рекламы. Такого рода связи называют статистическими. Они проявляются в том, что при изменении значения фактора изменяется распределение результативного признака. Виды связей: 1. Функциональные (жестко детерминированные) – связи, при которых определенное значение факторного признака соответствует определенному значению результативного признака. Эти связи можно выразить в виде определенных формул, например: Q=qp. Где Q - стоимость продукции, q -физический объем продукции, р - цена. 2. Стохастические или статистические (корреляционные) – это связи, при которых факторному признаку соответствует не одно конкретное значение результативного признака, а их совокупность. Эти связи нельзя выразить определенными формулами. Они проявляются лишь в массовых явлениях. Например, затраты на рекламу и объем продаж. Виды связей (по общему направлению факторного и результативного признаков):Прямые связи - направление изменения факторного и результативного признаков совпадает. Обратные связи - направление изменения факторного и результативного признаков не совпадает. По форме связи могут быть линейные и нелинейные. Пути возникновения корреляционной связи: 1. Причинная зависимость результативного признака от факторного признака. 2. Сопряженность, возникающая при наличии общей причины. 3. Взаимосвязь признаков, каждый из которых и причина, и следствие. Методы измерения связей количественных признаков: 1. Прямые (балансовый метод, индексный метод) – используется для измерения функциональных связей. Индексный метод – аналитические индексы. 2. Косвенные методы – основаны на соответствии вариации значения факторного и результативного признака. Это: а. Метод параллельных рядов, б. Метод аналитической группировки, в. Корреляционно-регрессионный анализ. 1 Э В 1 2 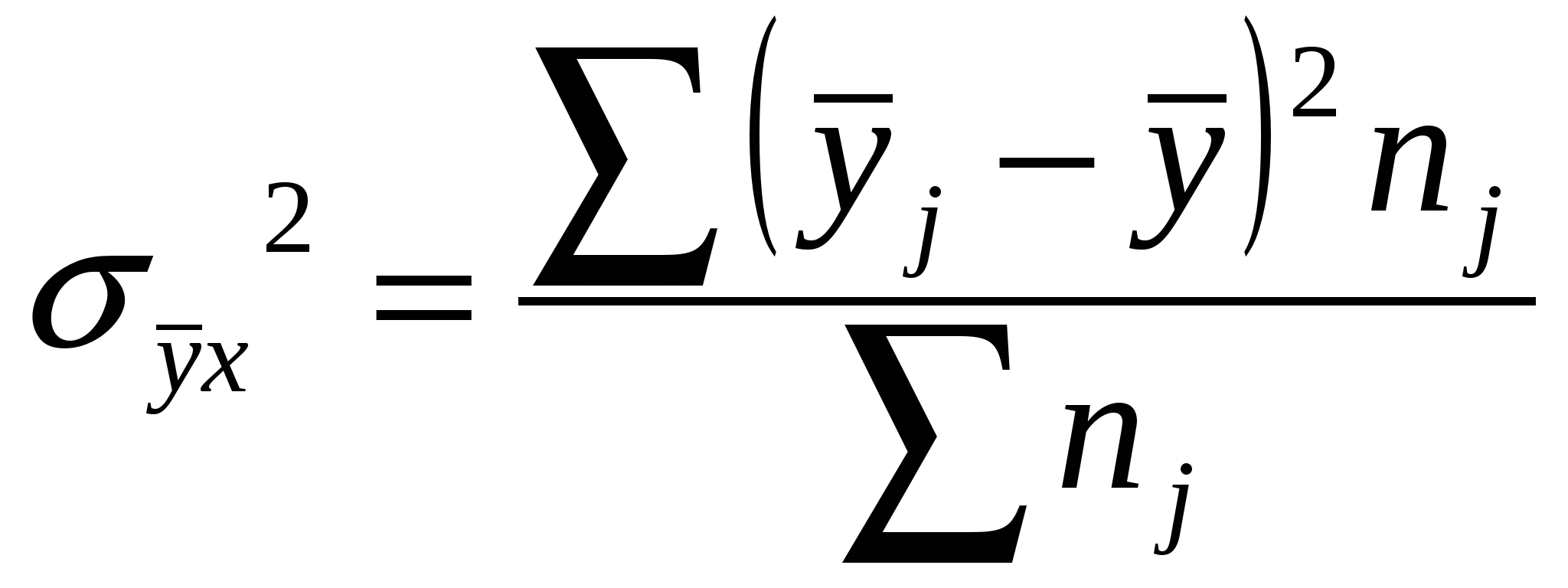 . Межгрупповая дисперсия, характеризует влияние данного фактора на результат, заложенного в основу группировки. Рассчитывается по сгруппированным данным: . Межгрупповая дисперсия, характеризует влияние данного фактора на результат, заложенного в основу группировки. Рассчитывается по сгруппированным данным: 3 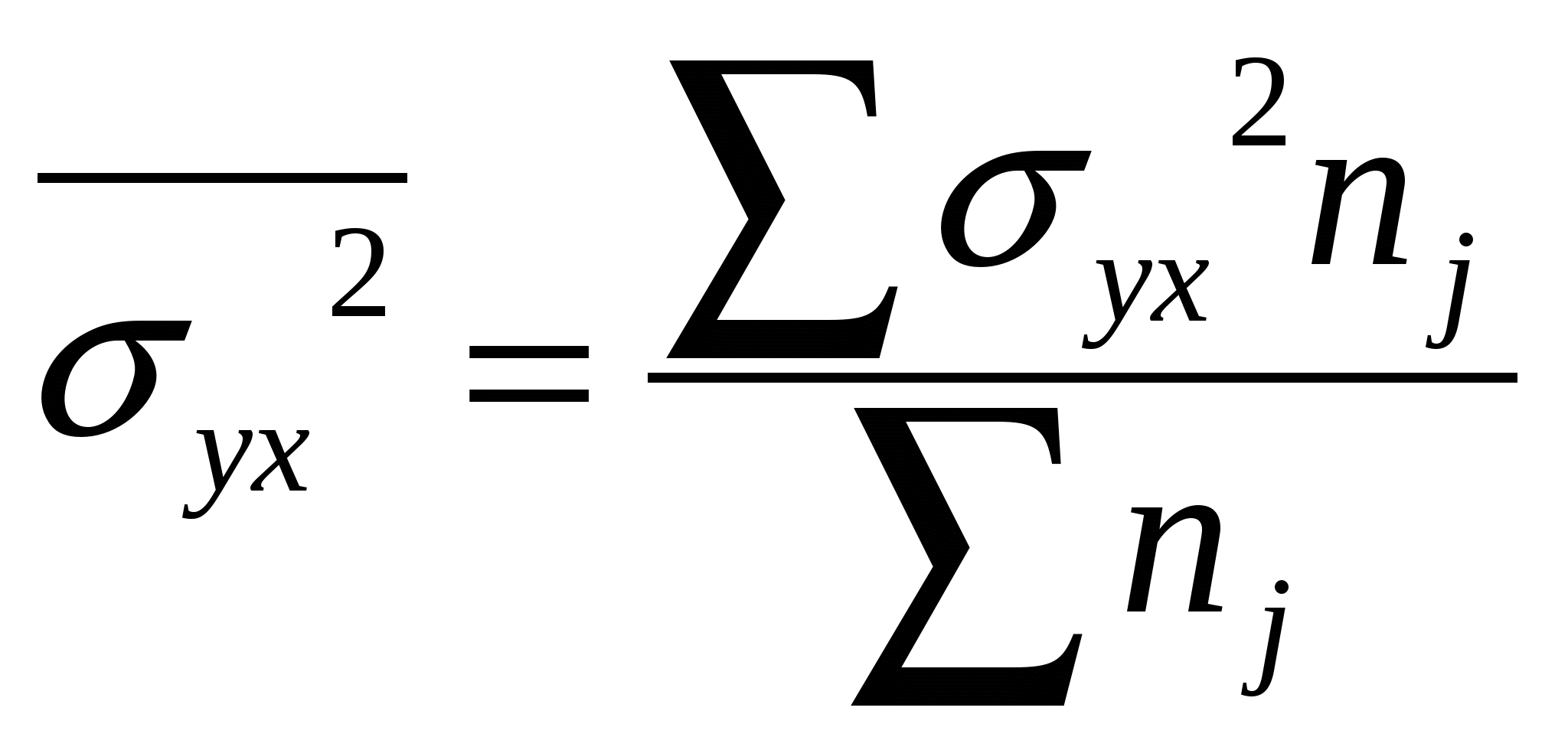 . Средняя (остаточная) из внутригрупповых дисперсий характеризует влияние прочих неучтенных факторов: . Средняя (остаточная) из внутригрупповых дисперсий характеризует влияние прочих неучтенных факторов:К 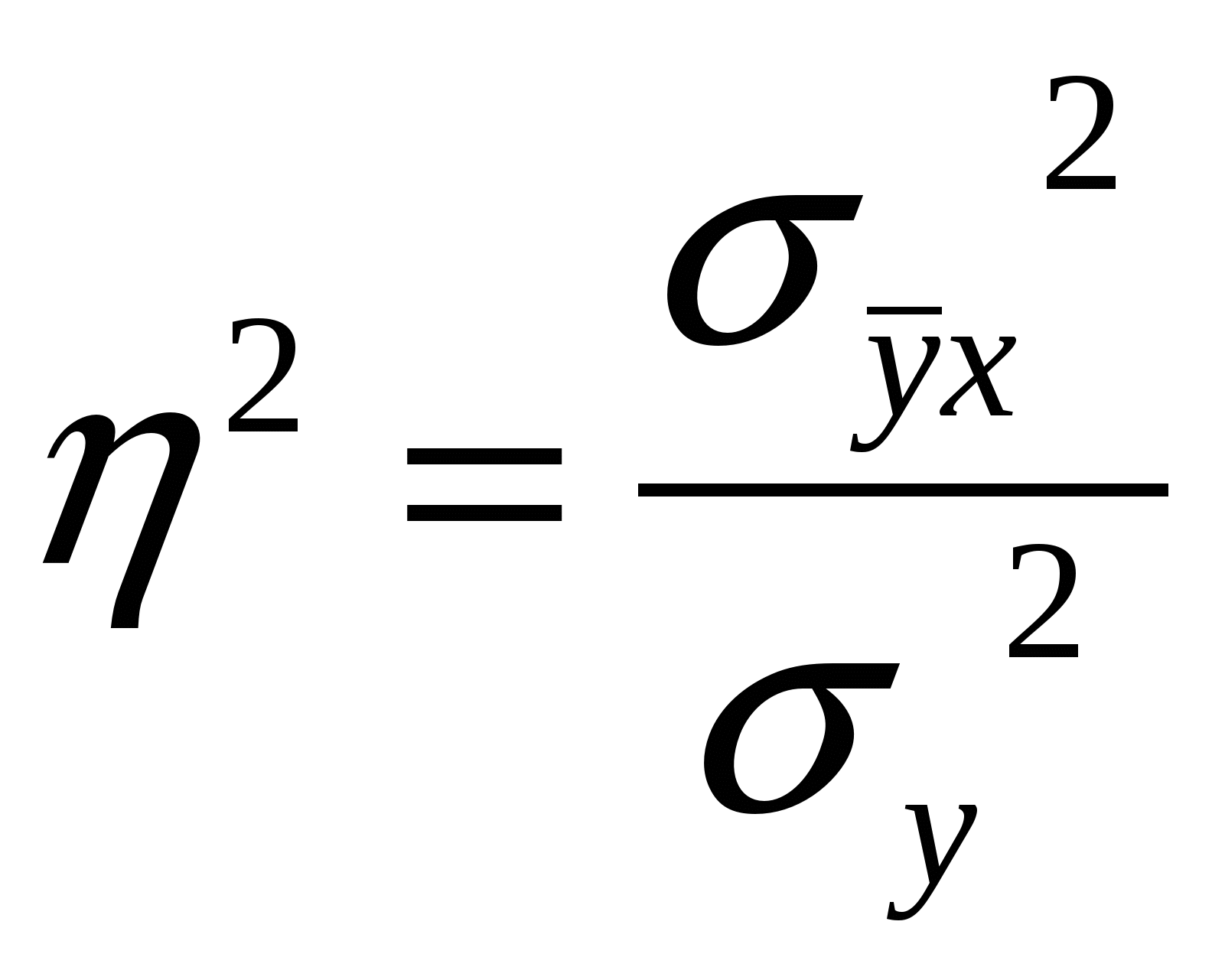 оэффициент детерминации характеризует долю факторной вариации в общей вариации результата: оэффициент детерминации характеризует долю факторной вариации в общей вариации результата:Эмпирическое корреляционное отношение: Если n=1, связь функциональная. Если до 0,3 – связь слабая. Если от 0,3 до 0,5 – умеренная. Если от 0,5 до 0,7 – заметная. Если от 0,7 до 0,9 – высокая. Если от 0,9 до 1 – весьма высокая. Близкая к функциональной. Недостатки аналитической группировки: 1.Предполагает только линейную зависимость между признаками. 2. На основе аналитической группировки невозможно прогнозировать явление. 20. Основы корреляционно-регрессионного анализа. Вычисление и интерпретация параметров парной линейной регрессии. Показатели корреляции. Регрессионный анализ заключается в определении аналитического выражения связи между явлениями, в котором изменение одной величины (зависимой) обусловлено влиянием одной или нескольких независимых величин. Условия применения: - Наличие данных по достаточно большой совокупности; -Однородность совокупности; -Необходимость подчинения распределения совокупности по факторному и результативному признакам нормальному закону распределения. Задачи: - Измерение параметров уравнения, выражающего связь между признаками. Эта задача решается оценкой параметров уравнения регрессии; - Измерение тесноты связи между признаками. Данная задача решается оценкой показателей корреляции. Парная корреляция – это изучение корреляционной связи между двумя переменными. Формулы расчета параметров уравнения параной регрессии: а Коэффициент детерминации показывает долю вариации (дисперсии) результативного признака, объясняемую регрессией в общей вариации результата. 2 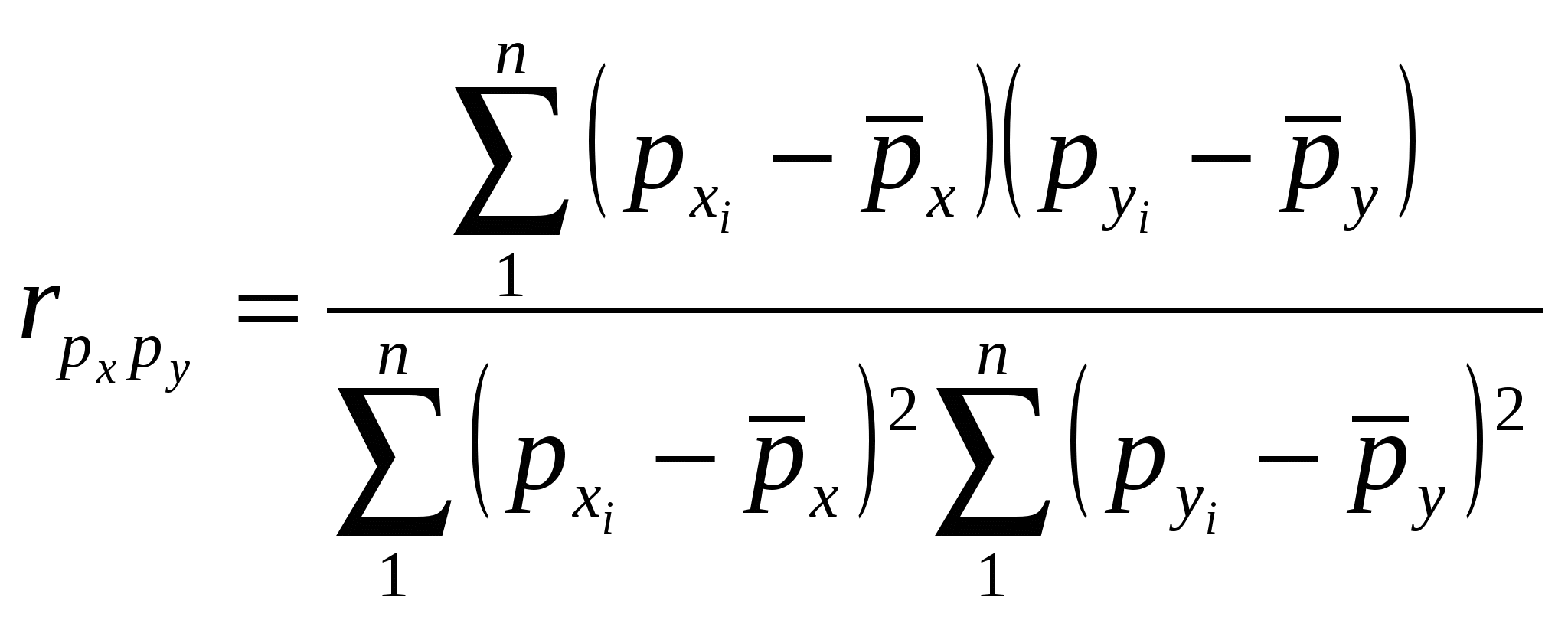 1. Статистический анализ неколичественных переменных. В практических задачах все чаще требуется измерение связей неколичественных переменных, измеренных на номинальных и порядковых шкалах. Это вызвано повышением внимания к изучению социальных процессов, где велика доля нечисловой информации. Развитие конкурентных рынков способствовало разработке методик построения рейтингов фирм, банков, учебных заведений. Рейтинг – по сути порядковая переменная, и для изучения зависимости рейтинга от каких-либо характеристик должны использоваться меры связи, предназначенные для порядковых переменных. При этом единицам совокупности присваиваются ранги по разным признакам, т.е. порядковые номера единиц совокупности в ранжированном ряду. Связь между ними определяется коэффициентом корреляции рангов.Коэффициент корреляции рангов Спирмена: 1. Статистический анализ неколичественных переменных. В практических задачах все чаще требуется измерение связей неколичественных переменных, измеренных на номинальных и порядковых шкалах. Это вызвано повышением внимания к изучению социальных процессов, где велика доля нечисловой информации. Развитие конкурентных рынков способствовало разработке методик построения рейтингов фирм, банков, учебных заведений. Рейтинг – по сути порядковая переменная, и для изучения зависимости рейтинга от каких-либо характеристик должны использоваться меры связи, предназначенные для порядковых переменных. При этом единицам совокупности присваиваются ранги по разным признакам, т.е. порядковые номера единиц совокупности в ранжированном ряду. Связь между ними определяется коэффициентом корреляции рангов.Коэффициент корреляции рангов Спирмена: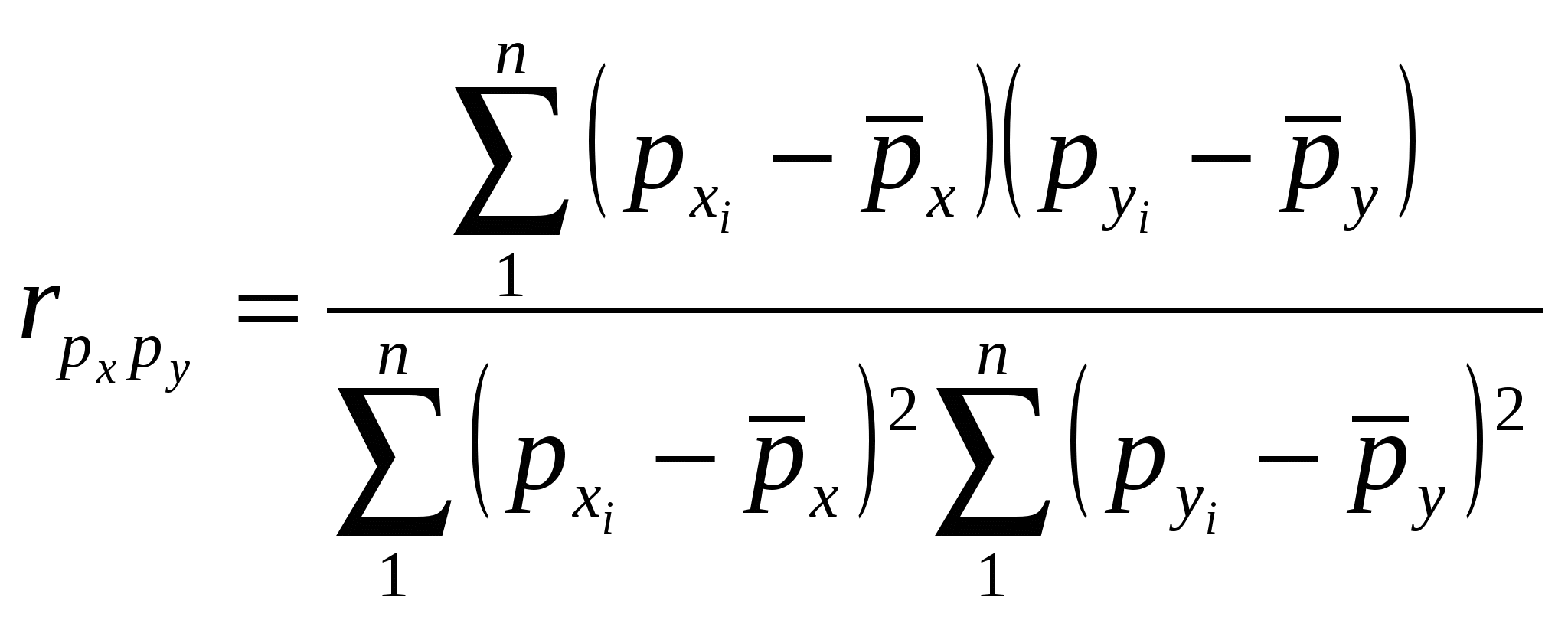 г П 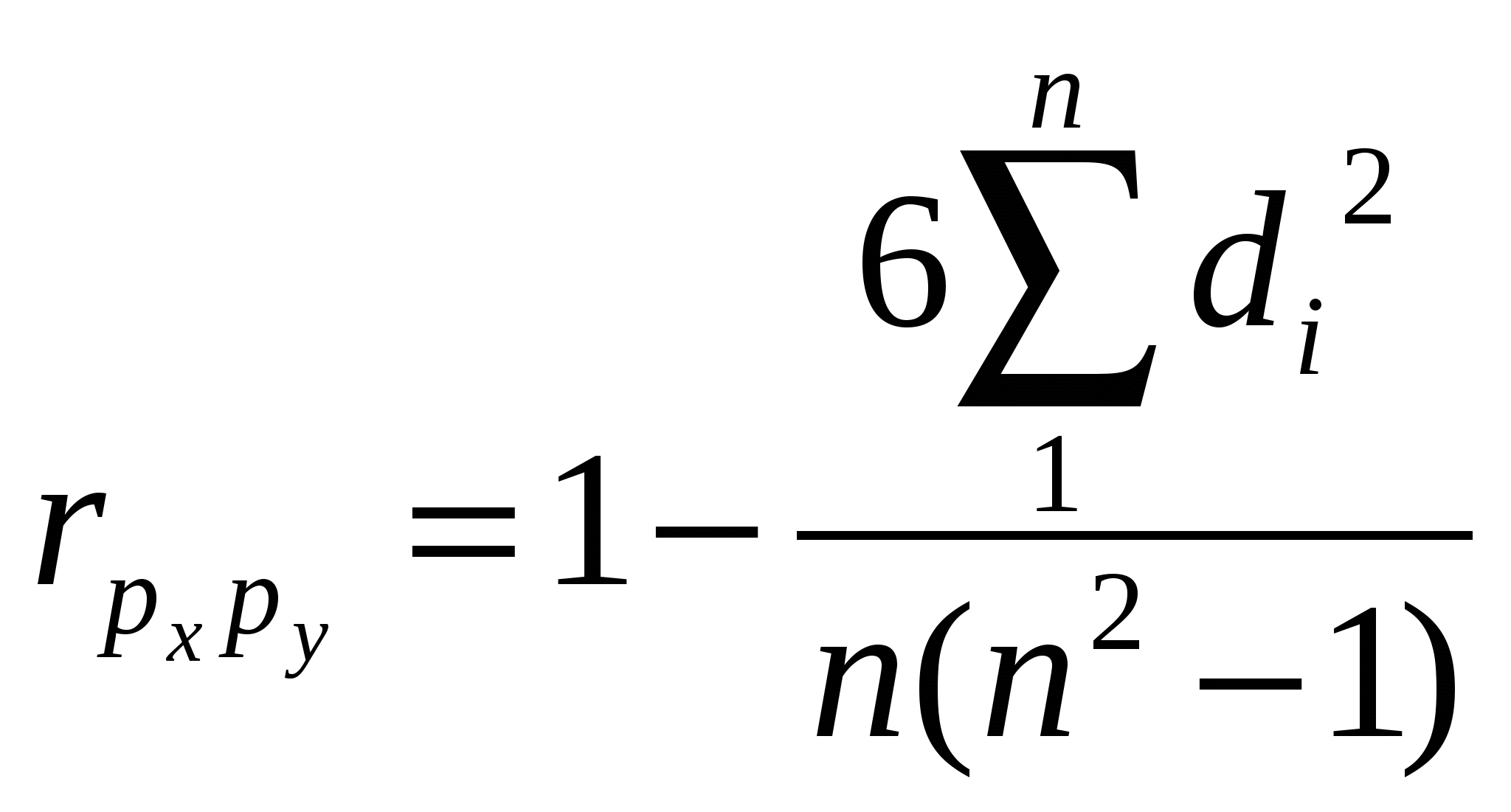 утем преобразования приведенной формулы Спирмен получил выражение коэффициента ранговой корреляции: утем преобразования приведенной формулы Спирмен получил выражение коэффициента ранговой корреляции: З П 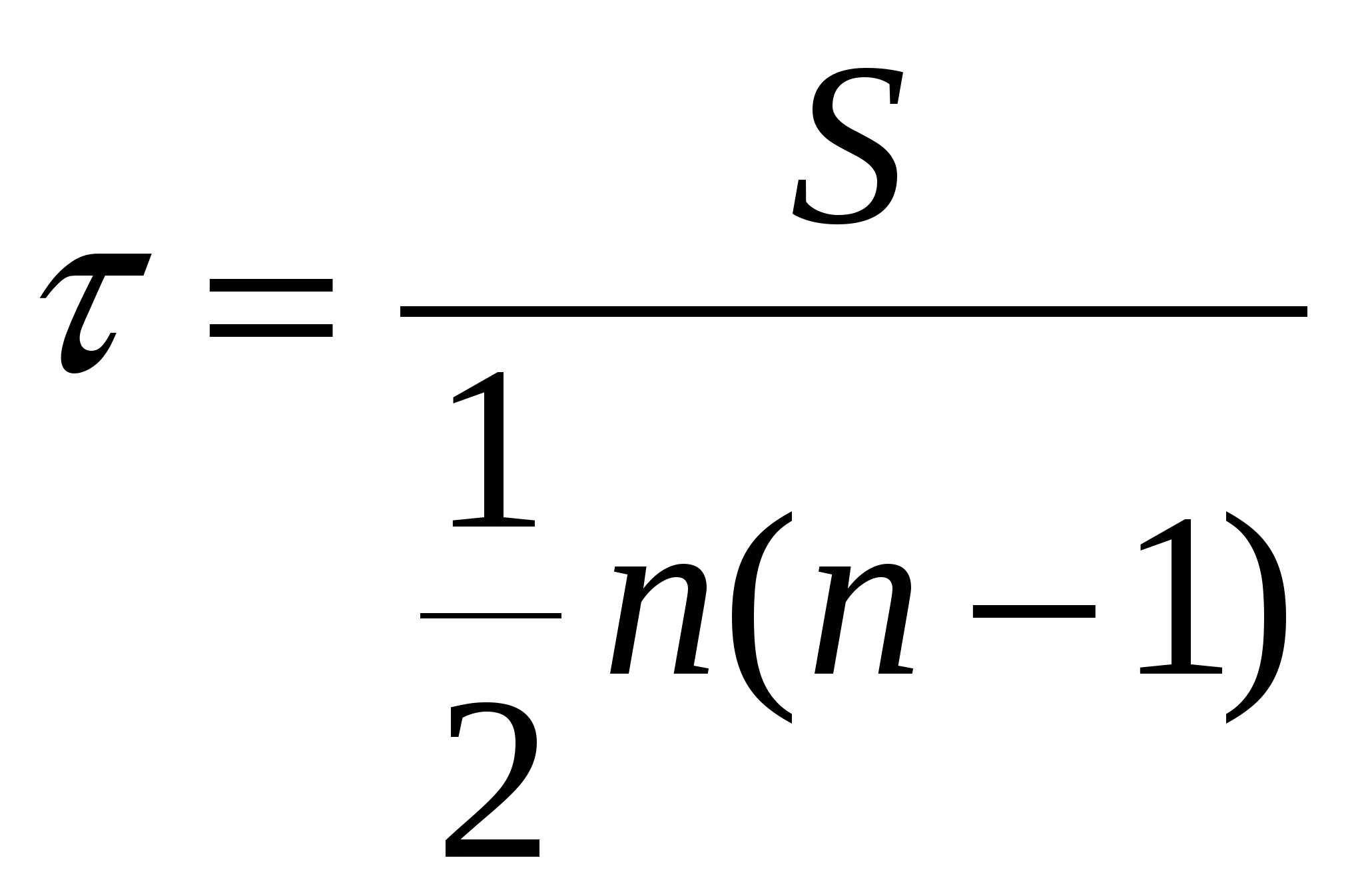 о таблице распределения Стьюдента находится критическое значение t – критерия. Если , то значим. При определении о таблице распределения Стьюдента находится критическое значение t – критерия. Если , то значим. При определении S – фактическая сумма рангов, Связь считается подтвержденной, если 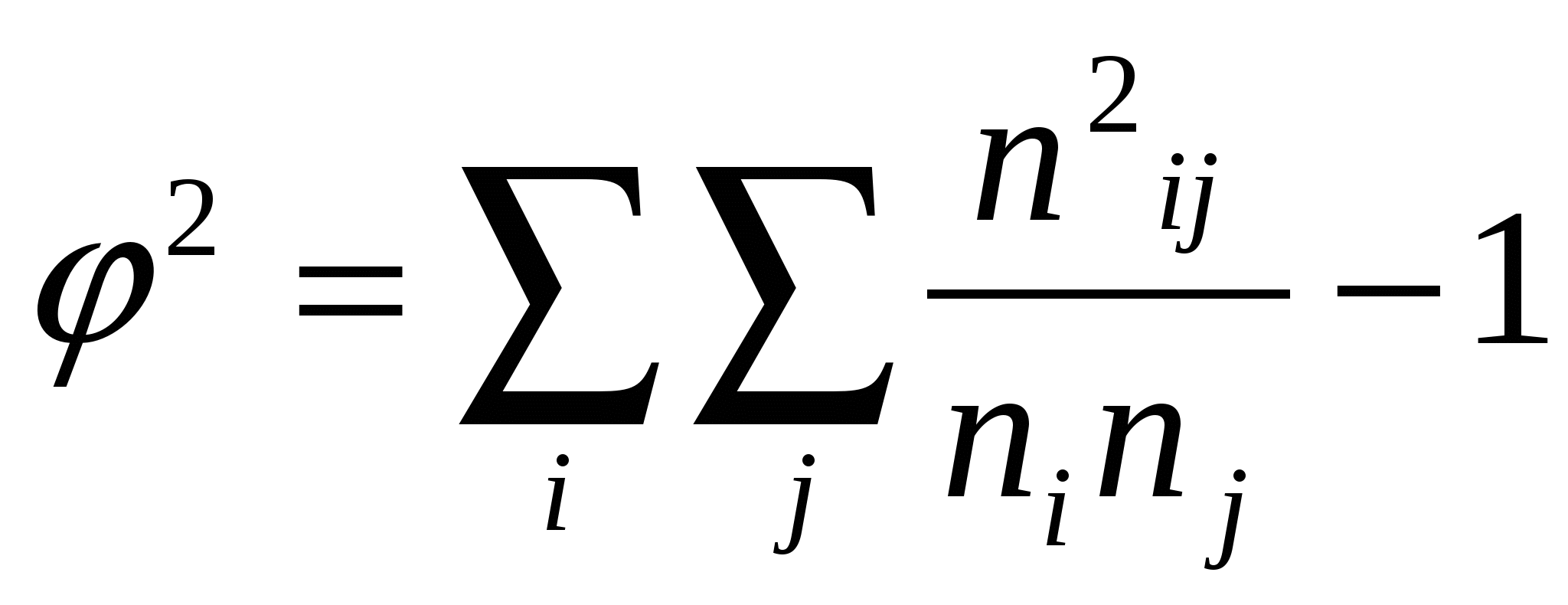 , где I – номер категории по признаку х, i=1…m, j – номер категории по признаку у, j=1…p. , где I – номер категории по признаку х, i=1…m, j – номер категории по признаку у, j=1…p. 22. Выборочное наблюдение, его использование в практике статистики. Порядок проведения выборочного наблюдения. Выборочное наблюдение – это научно обоснованный способ несплошного наблюдения, при котором обследуется не вся совокупность, а лишь часть ее, отобранная по определенным правилам выборки и обеспечивающая получение данных, характеризующих всю совокупность в целом. Трактовка данных как выборочных является основой деления статистики на описательную (дескриптивную) и выводную (аналитическую). Описательная статистика является инструментом описания совокупности, по которой у исследователя полностью имеются исходные данные. Аналитическаястатистика– позволяет по данным выборки делать заключения о большей совокупности, по которой исследователь не имеет исчерпывающих наблюдений. Преимущества выборочного наблюдения: -Выигрыш во времени, -Снижаются затраты на сбор и обработку данных, -Снижается риск ошибки регистрации, -Выборочный метод – единственный метод при испытаниях, связанных с уничтожением продукции. Порядок проведения выборочного наблюдения: -Определение единицы наблюдения и границ генеральной совокупности, -Составление программы наблюдения и инструкций, -Определение основы для проведения выборки – списка единиц генеральной совокупности, сведений об их размещении и.т.д., -Установление допустимого размера погрешности и определения объема выборки, -Обоснование выбора метода и способа отбора единиц в выборку, -Установление сроков проведения наблюдения, -Определение потребности в кадрах, их подготовка, -Отбор единиц в выборку, -Сбор информации по единицам выборочной совокупности, проверка полноты охвата отобранных единиц, - Построение обобщающих показателей на основе выборки, - Расчет ошибки выборки, - Распространение результатов выборочного наблюдения на генеральную совокупность с определенной вероятностью. 23. Способы и методы отбора единиц в выборочную совокупность. Различают два способа отбора: повторный (схема «возвращенного шара»: после отбора какой-либо единицы она возвращается в генеральную совокупность и снова может быть отобранной) и бесповторный (отобранная единица не возвращается в генеральную совокупность, и тем самым вероятность попасть в выборку для оставшихся единиц увеличивается с каждым шагом отбора). Виды выборки: -Собственно-случайная выбора (в случайном порябке выбираются ед совокуп), -Механическая (периодическая) выборка (данные отбираются через определенный шаг отбора), - Районированная(типическая) выборка – самая точна, - Гнездовая(серийная) – используется группа единиц совокупности, попавшие в выборку серии обследуются полностью. Самая неточная, -Многоступенчатая – на каждом этапе используется своя единица отбора. Используется в бюджетных обследованиях и при изучении проблем занятости, -Многофазовая -единица отбора одна и та же, но меняется прогр бследования, - Квотная – нарушается принцип случайности. Используется в маркетинге.
В О Д | |||||||||||