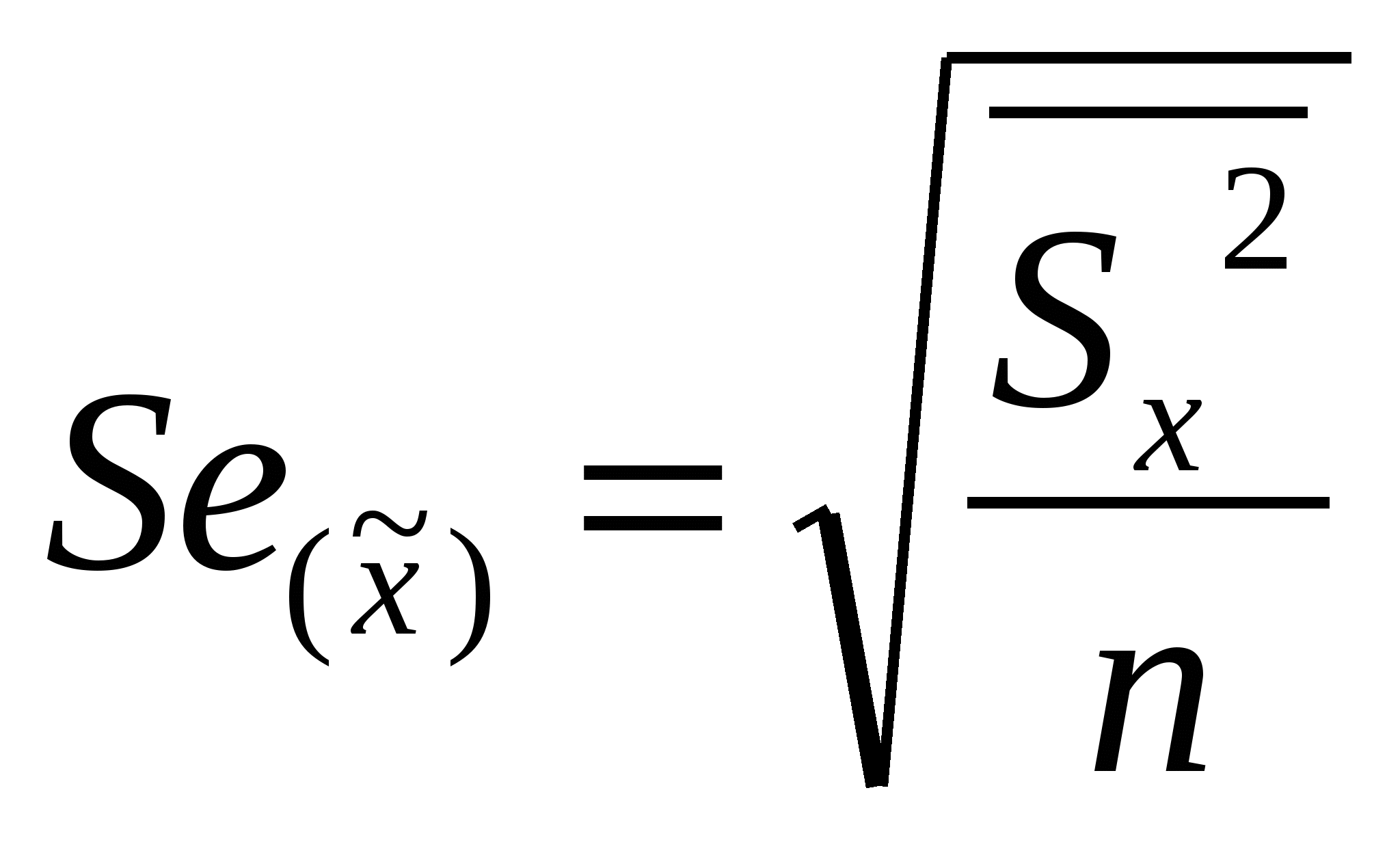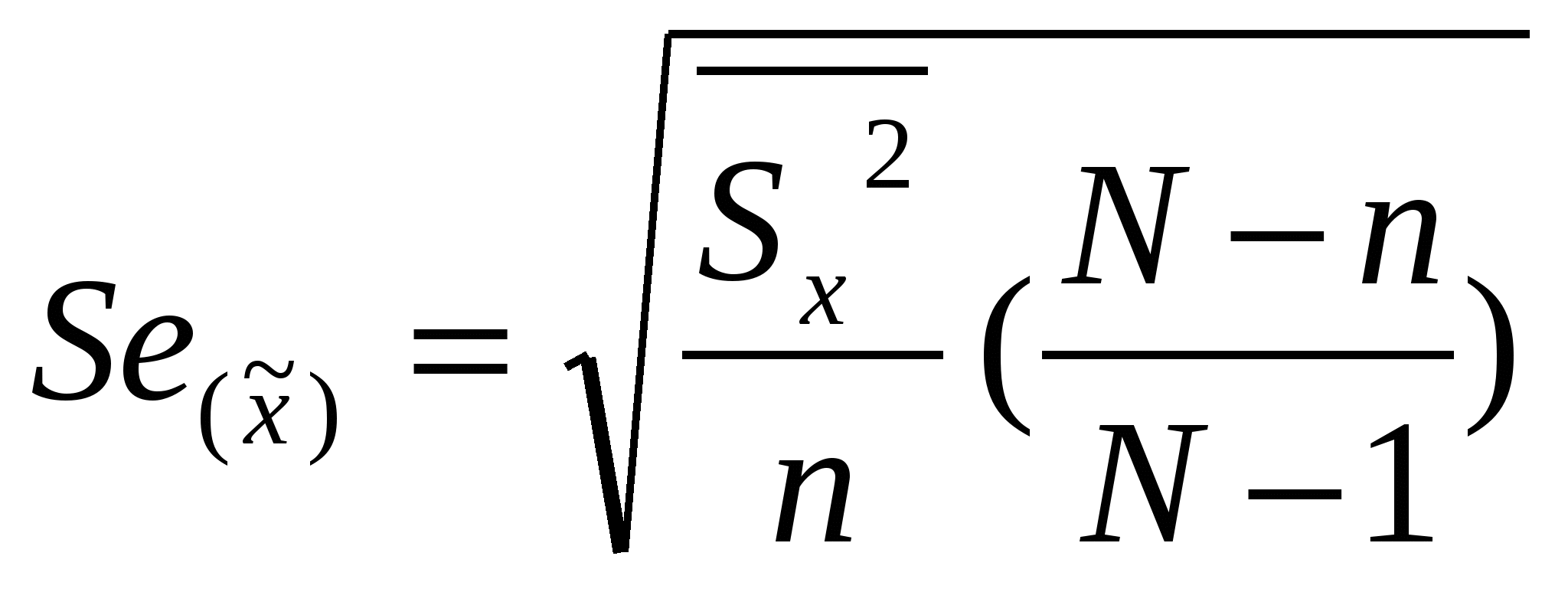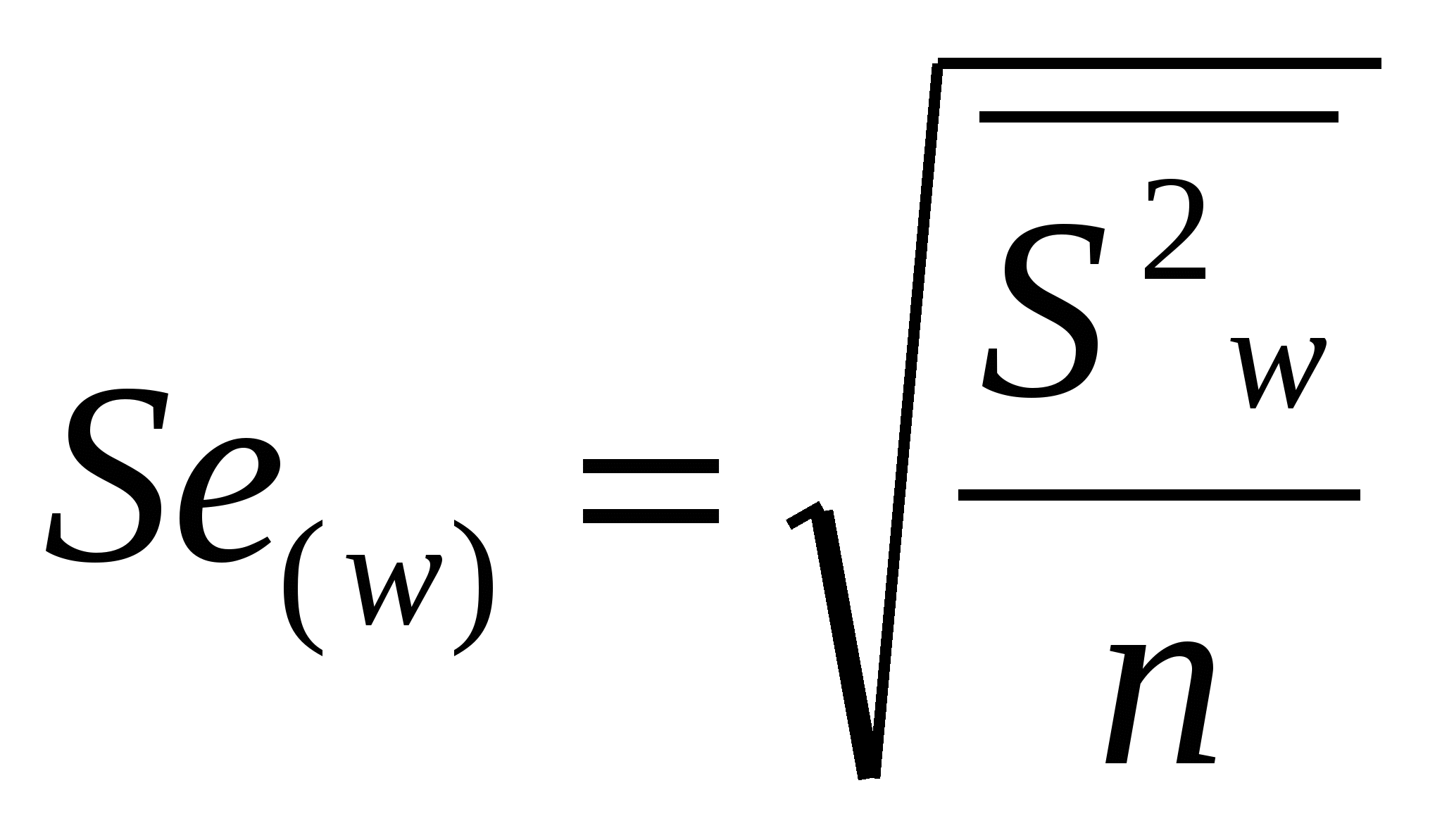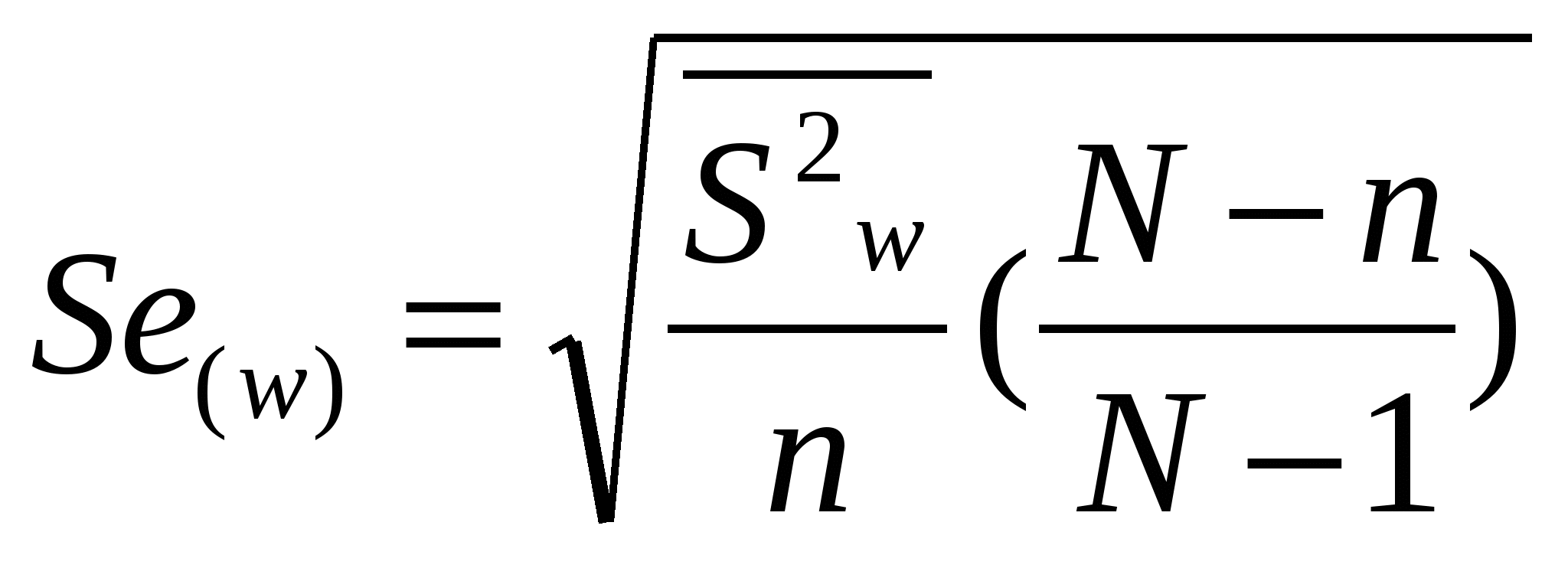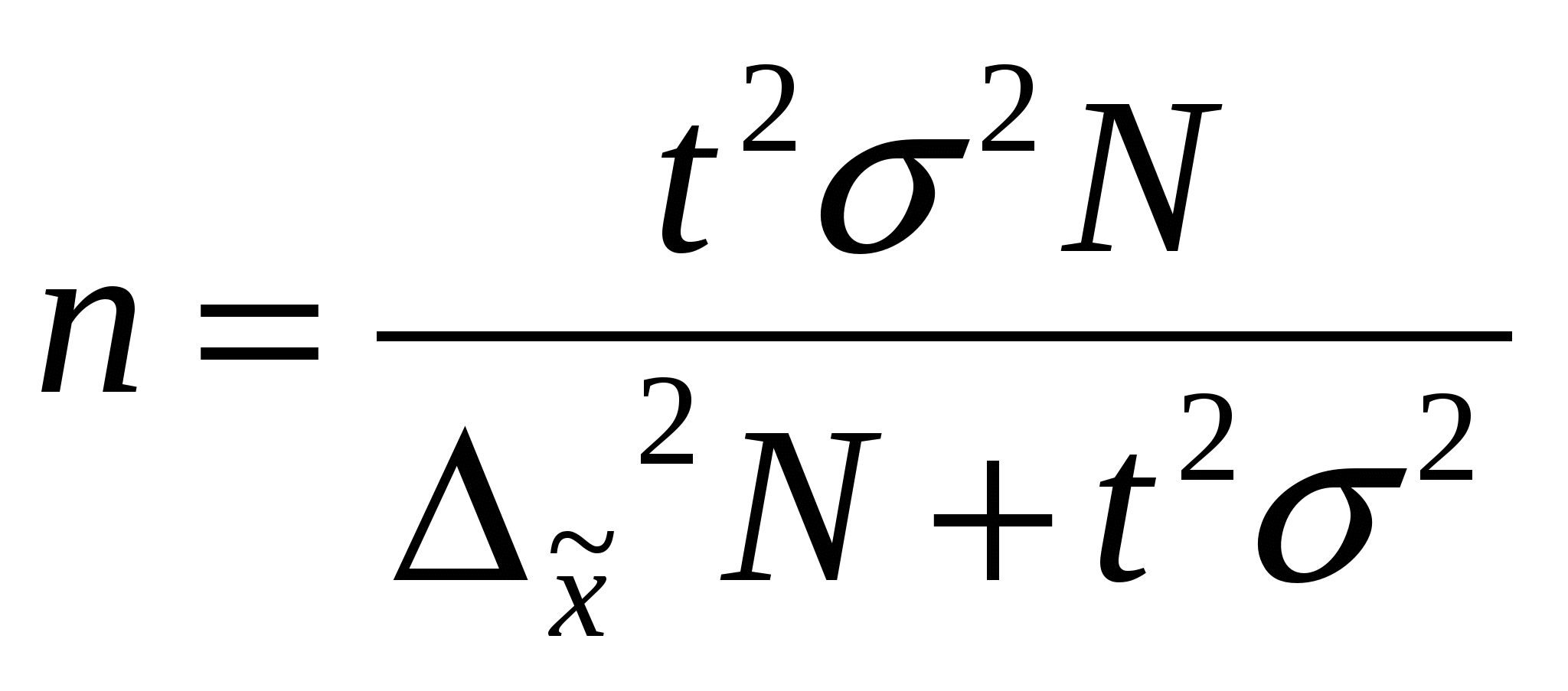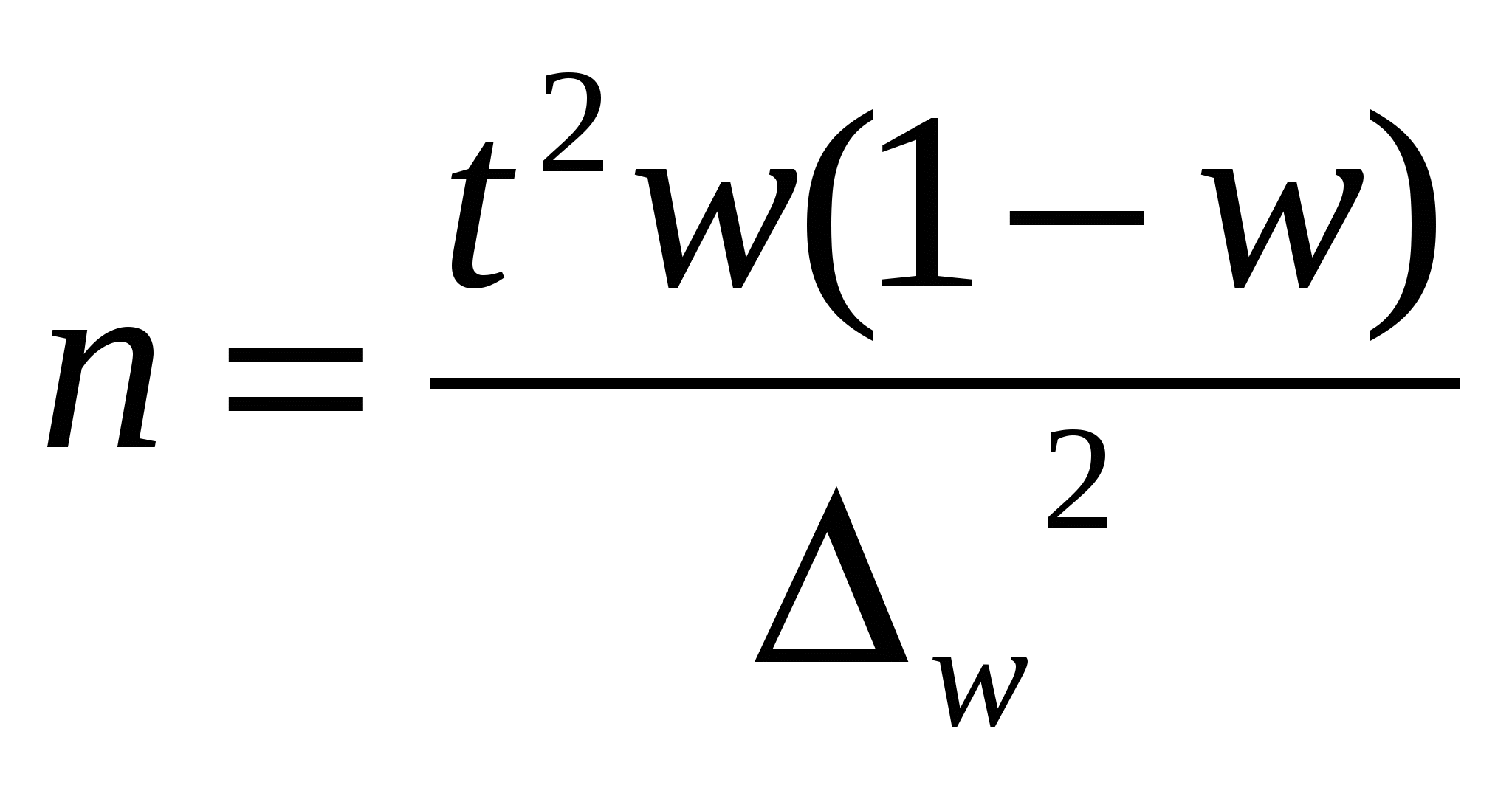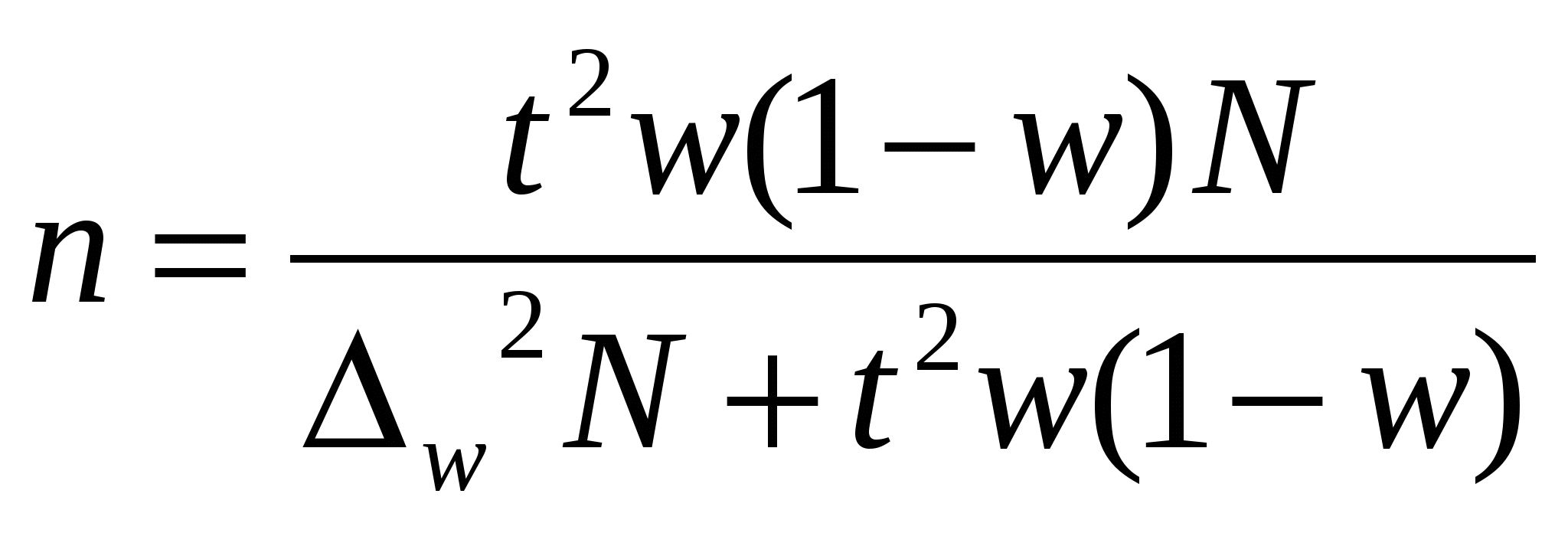Шпора по статистике. 1. Понятие об учете, виды учета. Статистический учет, его значение, задачи и особенности. Организация статистической деятельности в России
 Скачать 0.77 Mb. Скачать 0.77 Mb.
|
|
2 Г  де t – нормированное отклонение (коэффициент доверия). Определяется по таблице значений интеграла вероятностей. Расчет средней ошибки выборки: де t – нормированное отклонение (коэффициент доверия). Определяется по таблице значений интеграла вероятностей. Расчет средней ошибки выборки:R число равных серий в генеральной совокупности, r – число серий в выборке 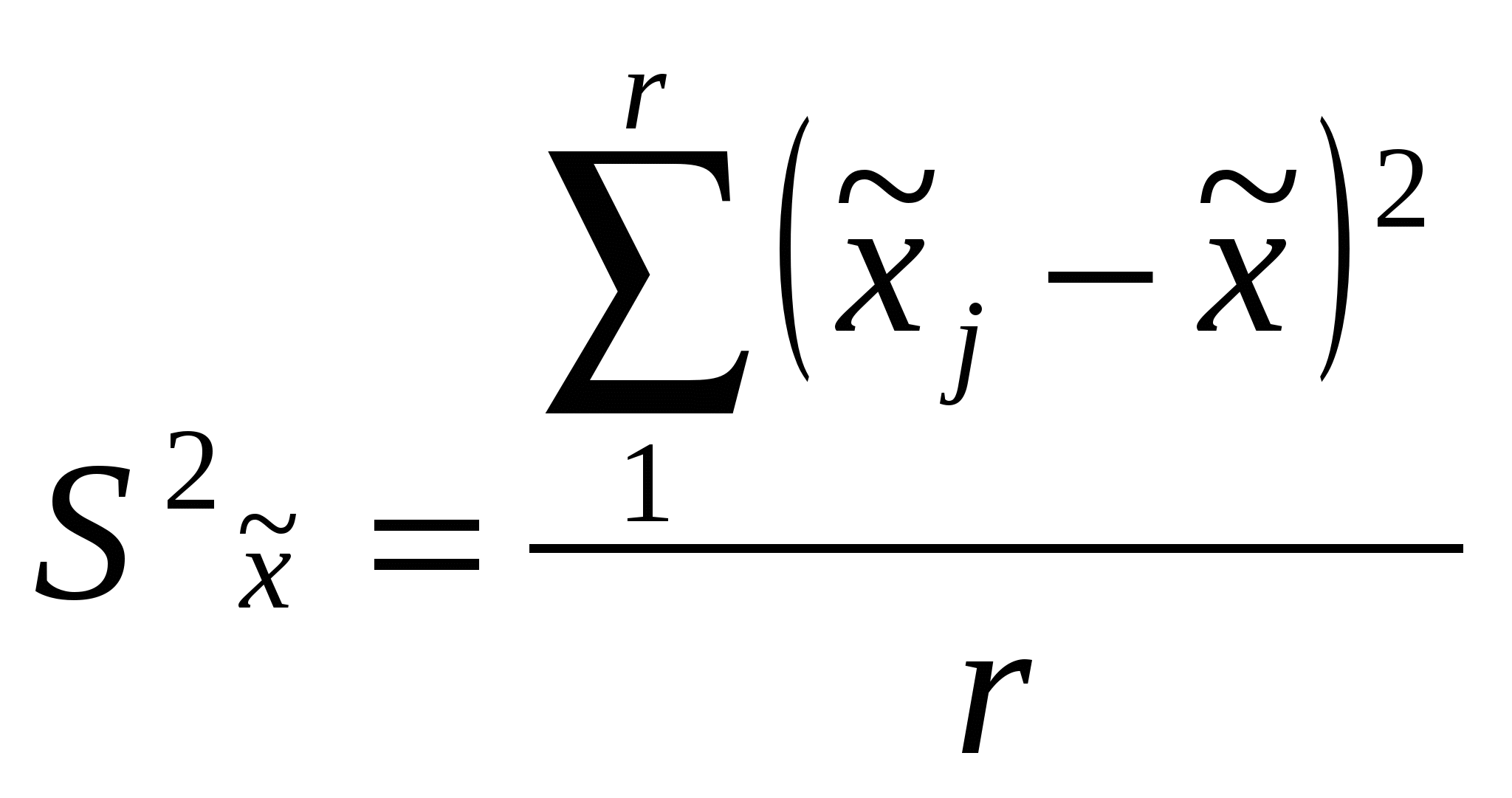 -межсерийная дисперсия для средней величины (число серий – одинаково). -межсерийная дисперсия для средней величины (число серий – одинаково). 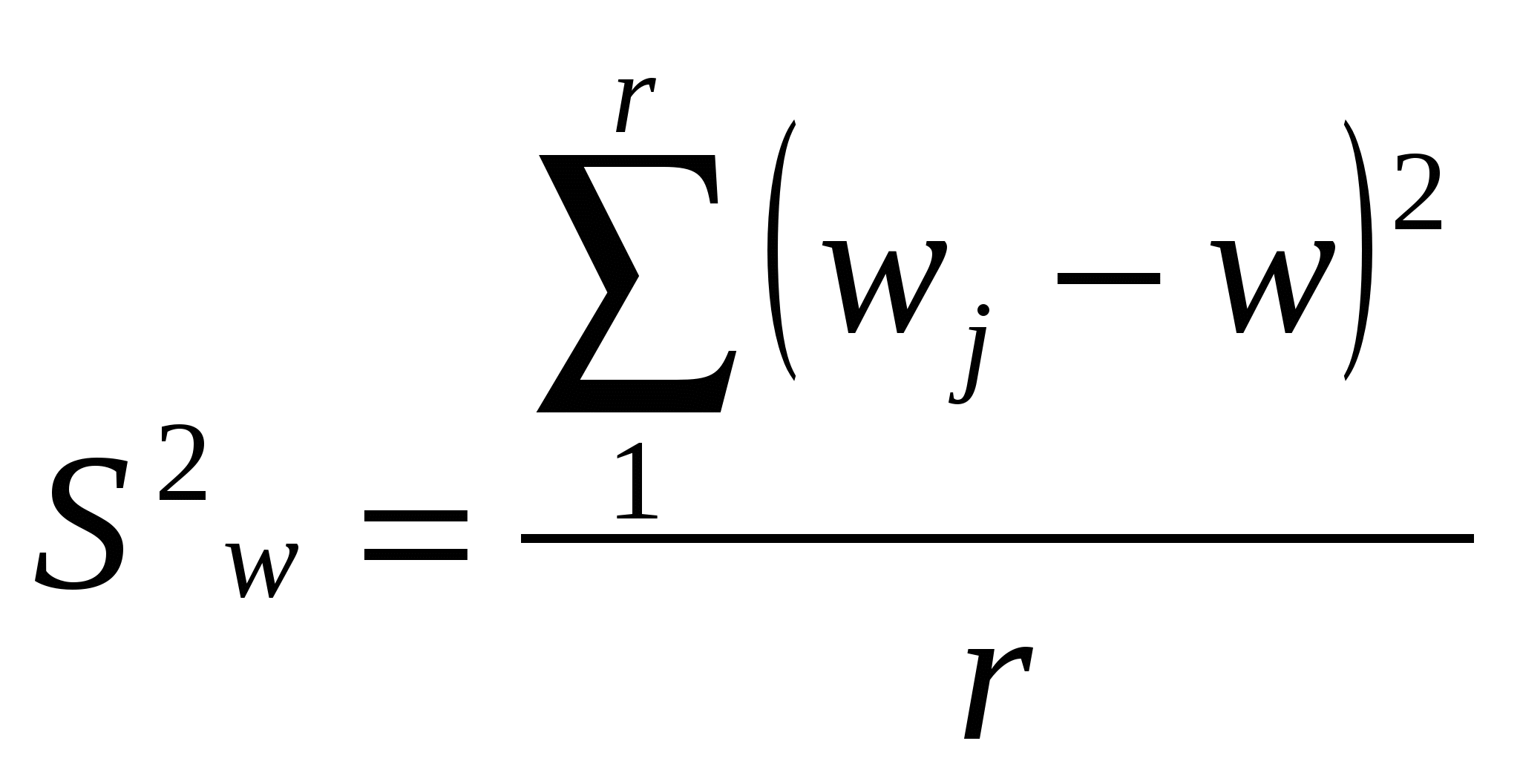 - межсерийная дисперсия для относительной величины (для доли), wj – доля единиц определенной категории в j-ой серии, - межсерийная дисперсия для относительной величины (для доли), wj – доля единиц определенной категории в j-ой серии, 2 - Г 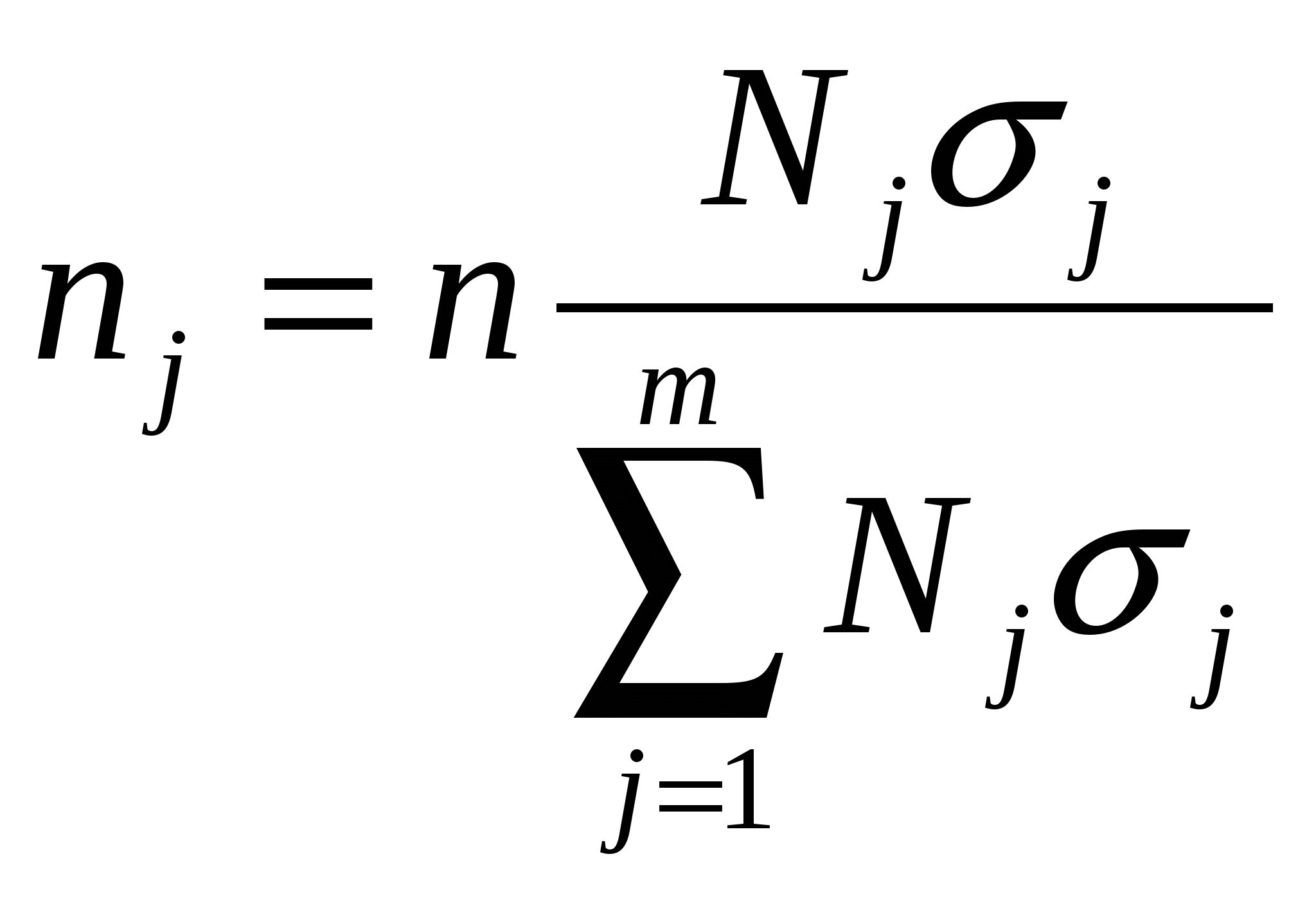 де м- число групп. -пропорционально численности группы и вариации признака в группе: де м- число групп. -пропорционально численности группы и вариации признака в группе: Расчет средней ошибки при типическом отборе, пропорциональном численности групп:
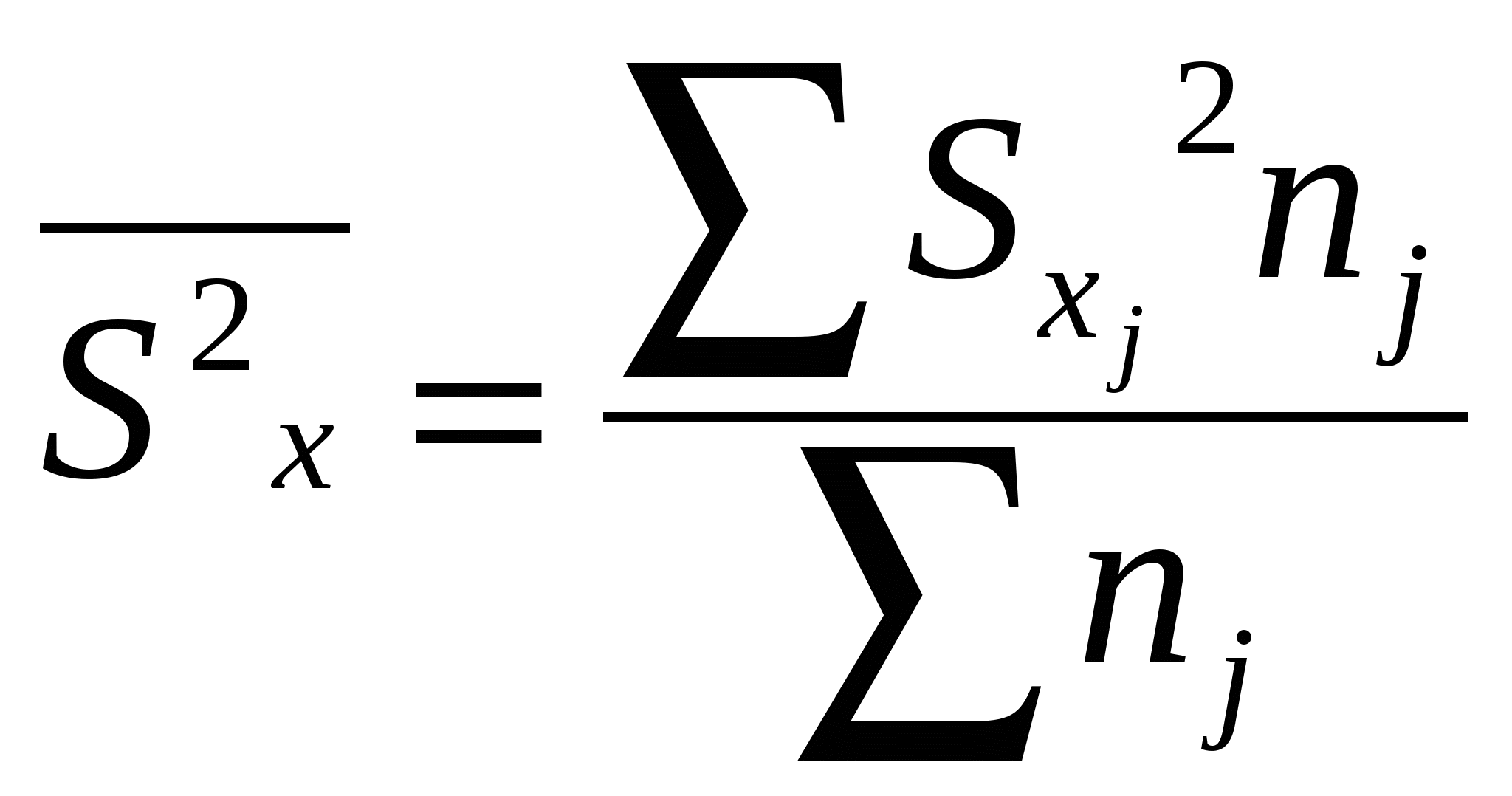 - - nj– численность выборки в j-ой группе, 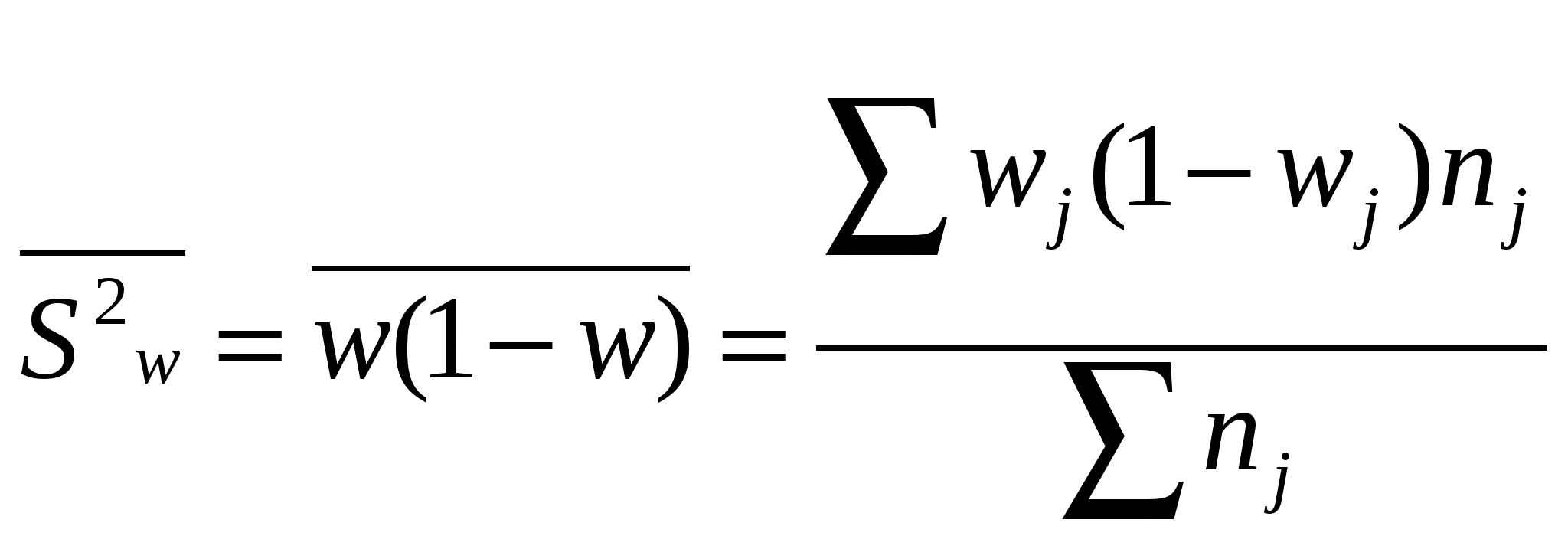 , ,
2 Р 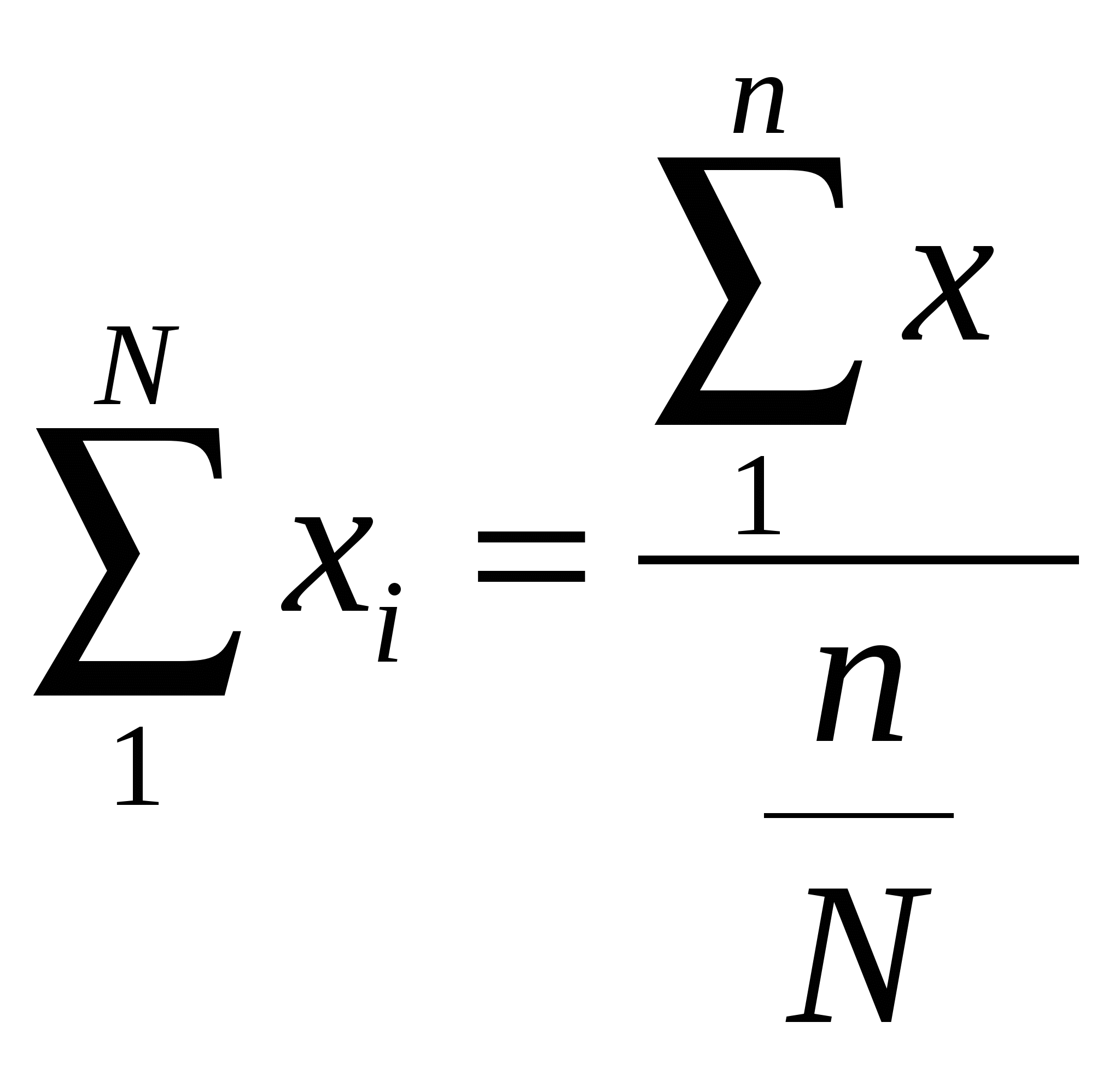 асчет объемных показателей на основе выборки: асчет объемных показателей на основе выборки: , 2   3 А И  3 33. Индексы цен в социально-экономическом анализе. Индексы широко используются в статистике при характеристике изменения цен во времени и пространстве, при характеристике изменения физического объема, для расчета изменения ВВП, индексы используются при анализе производительности труда, изменения зарплаты. При расчете индексов цен используются разные веса (Пааше, Ласпейреса). В настоящее время индекс потребительских цен рассчитывается по формуле Ласпейреса, он рассчитывается на основе определенного набора товаров и услуг, причем их стоимость не меняется. Индекс цен Пааше представляет собой сравнение агрегированных цен, взвешенных по физическим объемам текущего периода, а индекс цен Ласпейреса – сравнение агрегированных цен, взвешенных по физическим объемам базисного периода. Индексы цен Л и П в связи с различиями в структуре весов дают неодинаковые результаты. Фишером была предложена формула средней геометрической индексов Л и П. При использовании индекса Фишера удовлетворяется одно из требований теории индексов – независимость индекса от выбора базы равнения. 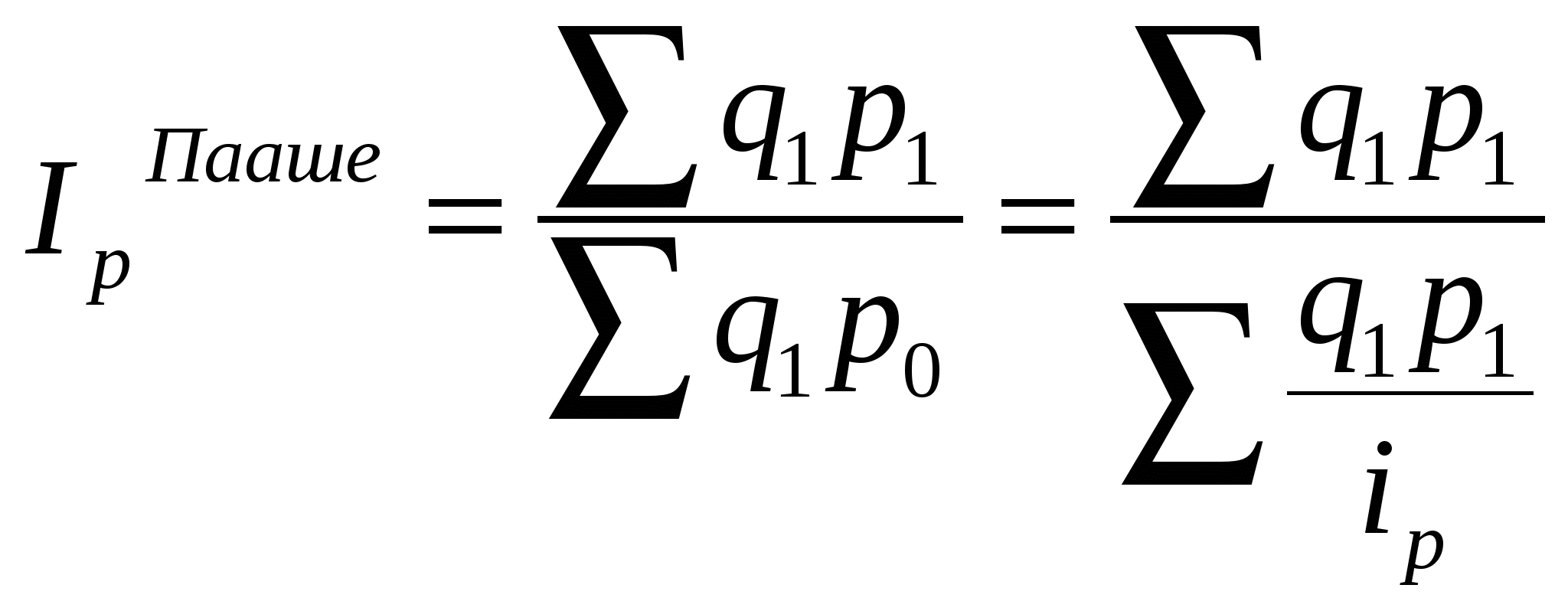 34. Индексы потребительских цен(назначение, источники информации, порядок расчета). Темпы повышения или снижения уровня жизни населения, обусловленные изменениями зарплаты, пенсий, можно правильно оценивать лишь с учетом изменения индекса потребительских цен (ИПЦ). На основе ИПЦ правительство корректирует внутреннюю политику в области финансов, денежного обращения, индексирует доходы различных социальных групп населения, оценивает уровень инфляции на потребительском рынке. Используется информация о ценах, доходах и расходах населения. Сбор информации производится на предприятиях сферы торговли и сферы услуг, в местах реализации товаров и услуг. Набор товаров и услуг, по которым регистрируются цены, состоит из трех групп: продовольственные товары (100), непродовольственные товары (201), платные услуги (81). Учет цен и товаров проводится по выборочному кругу городов и д.р. населенных пунктов, отобранных с учетом их представительности. Наблюдение осуществляется только в городских поселениях. В с/х. местности это нецелесообразна, т.к. требует значительного увеличения материальных и трудовых затрат. В крупных городах цены регистрируются еженедельно, в других – ежемесячно. Из всего набора товаров и услуг выделяют набор из 25 видов важнейших продуктов питания. Цены на них еженедельно регистрируются в СПб и Москве, столицах республик, областных, краевых городах и центрах АО. Госкомстат рассчитывает несколько ИПЦ – сводный ИПЦ по полному фиксированному набору потребительских товаров и услуг и этому же набору без товаров необязательного пользования (ювелирные изделия, легковые автомобили); ИПЦ для отдельных социально-экономических групп населения с различным уровнем доходов (10 групп семей); индекс стоимости прожиточного минимума. Порядок расчета: сначала определяют индивидуальные индексы цен товара/услуги по городу или району. Затем на основе индивидуальных индексов и территориальных весов определяются агрегатные индексы цен отдельных товаров/услуг в целом по региону. В качестве территориальных весов используется удельный вес численности населения обследуемой территории в общей численности населения РФ на начало года. Далее определяются сводные индексы цен в целом по группам товаров/услуг, а также ИПЦ по региону, району и РФ в целом. Расчет осуществляется ежемесячно к предыдущему месяцу, к соответствующему месяцу предыдущего года. Таким образом, ИПЦ рассчитывается путем последовательного агрегирования данных. Сначала определяют потоварные индексы, охватывающие все виды торговли, затем – индексы по товарным группам, потом строится сводный ИПЦ. 35. Задачи статистического изучения динамики. Динамический ряд: понятие, виды, графическое изображение. Обеспечение сопоставимости динамических рядов. Прогнозирование – это оценка будущего на основе глубоко анализа тенденций развития социально-экономических явлений и их взаимосвязей. Процесс прогнозирования предполагает выявление всевозможных альтернатив развития в перспективе для обоснованного их выбора и принятия оптимального решения. Прогнозирование ведется на основе использования широкого спектра информации. Но первоначальный этап всегда связан с анализом временных рядов, который позволяет охарактеризовать закономерность изменения явления во времени. Временной ряд также называется рядом динамики. Временной (динамический) ряд – ряд последовательно расположенных во времени числовых значений соответствующего показателя.Элементы временного ряда: уровни ряда (yt)- числовые значения того или иного показателя, время (t). Виды временных рядов: моментные, интервальные. Уровни динамического ряда должны быть сопоставимы: по территории, если изменились территориальные границы, то необходимо, например, пересчитать численность населения. Необходимо обеспечить сопоставимость по времени, с точки зрения методики расчета показателей. 3 К Т А Аналитический прирост показывает, на сколько единиц уровень одного периода больше или меньше уровня другого периода. Интенсивность изменения уровней временного ряда характеризуется темпами роста и прироста. Абсолютные приросты показывают скорость изменения уровней ряда в единицу времени. 3 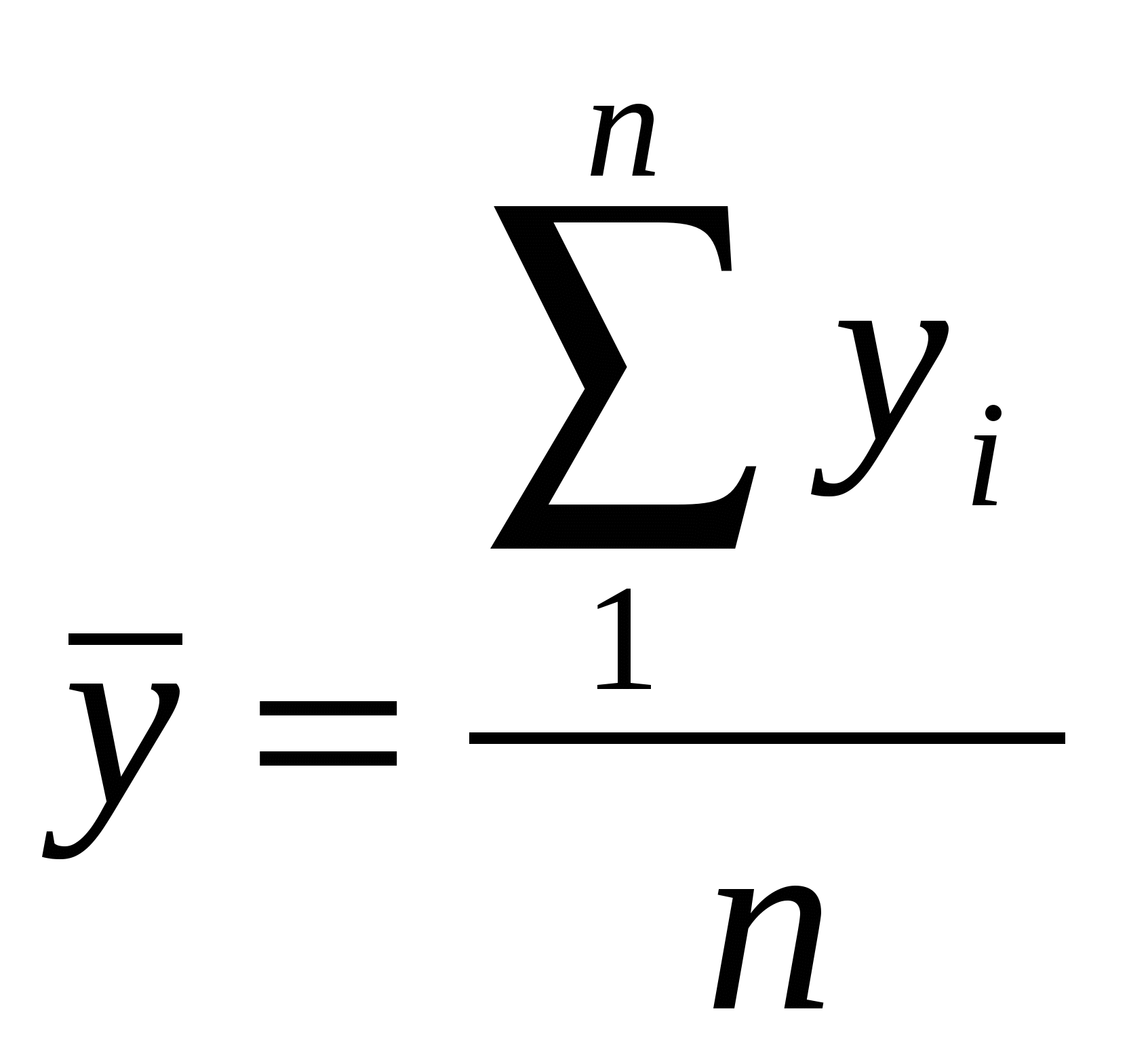 7. Динамические средние: порядок расчета и интерпретация. Средний уровень: -для интервального ряда из абсолютных величин: 7. Динамические средние: порядок расчета и интерпретация. Средний уровень: -для интервального ряда из абсолютных величин:yi - уровни ряда для i-го периода;n - число уровней в ряду. -для интервального ряда из относительных величин: x - yi - уровень моментного временного ряда; ti - период, в течение которого уровень остается неизменным, то есть период действия данного уровня. - - смежные парные средние, найдены как средняя арифметическая простая из двух рядом стоящих уровней. ti- период действия средних . - 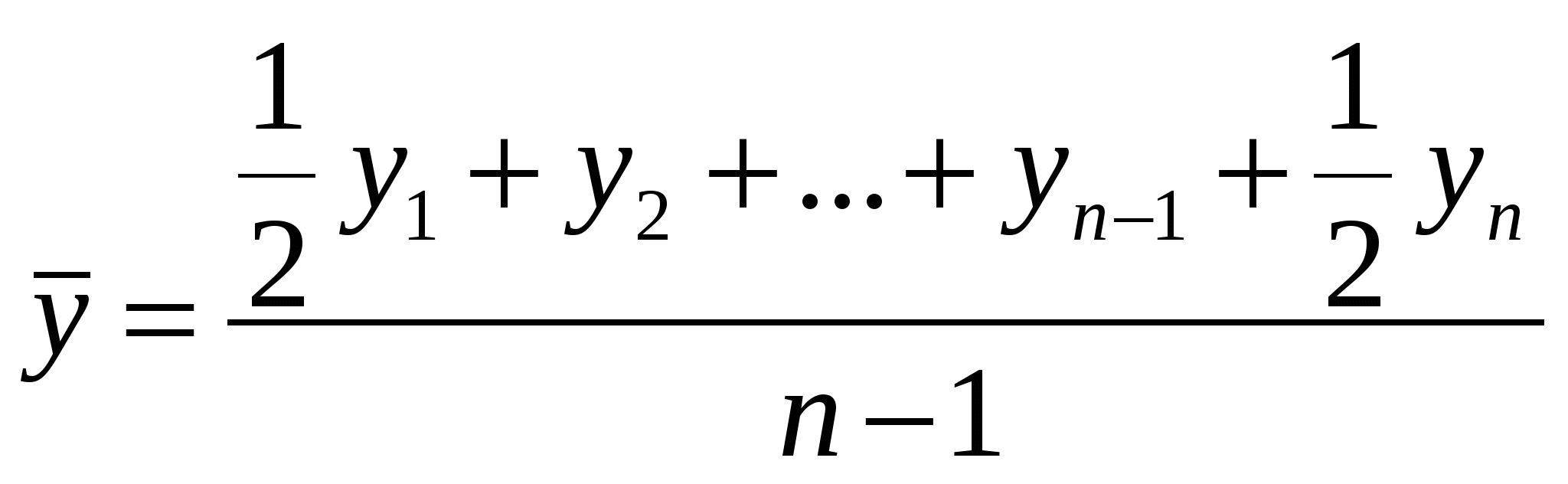 для моментного ряда, если интервалы между датами равны - средняя хронологическая: для моментного ряда, если интервалы между датами равны - средняя хронологическая: С где yn и y1- последний и первый уровни ряда. С | ||||||||||||||||||||||