Олигополия. 1 Понятие олигополии и ее характерные особенности
 Скачать 2.44 Mb. Скачать 2.44 Mb.
|
|
Лидерство в ценах Р  ис. 8. ис. 8.Гр. А      MC MCPl Dn D MRn  ql qd ql qd Гр. В   MC=Sf P  l l qf Лидерство в ценах - обычная практика на олигополистических рынках. Одна из фирм (не обязательно самая крупная) действует как ценовой лидер, который устанавливает цену, чтобы максимизировать свои собственные прибыли, в то время как другие фирмы следуют за лидером. Соперничающие фирмы назначают ту же цену, что и лидер, и работают при уровне выпуска, который максимизирует их прибыли при этой цене. Лидирующая фирма предполагает, что другие фирмы на рынке не будут реагировать таким образом, что изменят цену, которую она установила. Они решат максимизировать свои прибыли при цене, установленной лидером как данную. Модель лидерства в ценах называется частичной монополией, т.к. лидер устанавливает монопольную цену, основанную на его предельном доходе и предельных издержках. Прочие фирмы принимают эту цену как данную. Рис. 8 показывает, каким образом определяется цена при частичной монополии. Лидирующая фирма определяет свой спрос, вычитая то количество товара, которое продают другие фирмы при всех возможных ценах, из рыночного спроса. Кривая рыночного спроса D показана на рис. 8 на гр. А. Кривая предложения всех прочих фирм - Sf показана на гр. В (рис. 8). Количество товара, предлагаемое конкурентами фирмы-лидера, будет возрастать при более высоких ценах. Фирма-лидер реализует менее значительную долю рыночного спроса при более высоких ценах. На рис. 8 видно, что при цене Pl выпуск составляет qd ед. При этом кривая спроса на гр. В показывает, что количество товара, предлагаемое другими фирмами, будет равно qf=qd- ql. Количество товара, на который есть спрос на рынке, оставшееся для господствующей фирмы (“чистый спрос”), составляет ql ед. Эта точка находится на кривой спроса Dn. Кривая спроса тогда показывает, какой объем продаж может надеяться осуществить лидирующая фирма при любой цене после вычета продаж, произведенных другими фирмами. Фирма -лидер максимизирует прибыли путем выбора цены, которая делает предельный доход от удовлетворения чистого спроса, MRn, равным ее предельным издержкам. Следовательно, цена лидера равна Р1, и фирма-лидер продаст ql ед. продукции по этой цене. Прочие фирмы принимают цену Р1 как данную и выпускают qf ед. Лидерство в ценах можно также объяснить опасениями части меньших фирм насчет ответной реакции лидирующей фирмы. Это верно, когда лидирующая фирма может производить при более низких издержках, чем ее менее крупные конкуренты. Когда такое положение дел имеет место, то меньшие фирмы могут колебаться - снижать ли цену ниже лидера. Они понимают, что, хотя от снижения цены они выигрывают временно в продажах, но они проиграют войну цен, которую развяжет более крупная фирма, т.к. у них более высокие издержки и, следовательно, их минимальная цена выше, чем у более крупной фирмы. Меньшие фирмы на олигополистических рынках пассивно следуют за лидером иногда и потому, что они полагают ,что более крупные фирмы обладают большей информацией о рыночном спросе. Они не уверены насчет будущего спроса на свою продукцию и рассматривают изменение цены лидером как признак изменения спроса в будущем. 1.7. Ценообразование, ограничивающее вход в отрасль. Фирмы на олигополистических рынках могут устанавливать цены таким образом, что потенциальным новым производителям на рынке было невыгодно начать на нем торговлю. Для достижения этой цели фирмы на рынке могут устанавливать цены, которые не максимизируют их текущие прибыли. Вместо этого они устанавливают цены с таким расчетом, чтобы удержать новых производителей от входа на рынок и оказания понижающего воздействия на будущие прибыли. Фирмы либо сговариваются, либо следуют примеру других фирм при установлении таких цен, которые могли бы предотвратить вступление на рынок “чужаков”. Для достижения этой цели они оценивают минимально возможные средние издержки любого нового потенциального производителя и предполагают, что любой новый производитель примет цену, установленную существующими фирмами, и будет ее придерживаться. График А на рис. 9 показывает кривую LRAC потенциального нового производителя на олигополистическом рынке. Если фирма не может надеяться на цену на свой товар, равную по меньшей мере P`=LRACmin, то она сможет получать экономическую прибыль, войдя на рынок. График В (рис.9) показывает рыночный спрос на товар. Предположим, что существующие в отрасли фирмы организуют картель, чтобы максимизировать текущую прибыль. Тогда они установят цену Pm, соответствующую выпуску, при котором MR=MC. При этой цене продавалось бы Qm штук товара, и существующие фирмы делили бы общий выпуск между собой. Однако, поскольку Pm > LRACmin потенциальных новых производителей, то картель обречен на провал, если только не существует барьера для входа на рынок. Следовательно, фирмы знают, что устанавливать монопольную цену тщетно. При монопольной цене больше фирм войдет на рынок и предлагаемое для продажи количество товара возрастет, следовательно, цена и прибыли упадут. Рис. 9. гр. А    P`= LRACmin  Гр. В     Pm MC P` MR D  Qm Ql Ценой, ограничивающей вход на рынок, является цена, достаточно низкая, чтобы предотвратить появление на рынке в качестве продавцов новых потенциальных производителей. Предположим, что кривые средних издержек фирм выглядят так же, как и у новых производителей. В этом случае любая цена выше P` спровоцирует вход “чужаков”. Следовательно, фирмам отрасли придется удерживать цену на уровне P`=LRACmin. По этой цене они продадут Ql продукта, что больше, чем они продали бы, если бы цена была достаточно высокой, чтобы способствовать вступлению на рынок новых фирм, но тогда они получают нулевую экономическую прибыль. Если, однако, фирмы обладают преимуществом низких затрат, которых нет у новых потенциальных производителей, то они смогут извлекать в долгосрочном плане экономическую прибыль при цене P` и в тоже время удерживать потенциальных производителей от входа на рынок. Ценообразование, ограничивающее вход на рынок, показывает, каким образом опасения перед появлением на рынке новых конкурентов могут подтолкнуть максимизирующие прибыли фирмы временно не использовать свою монопольную власть на рынке. 2. Реклама при олигополии. На олигополистических рынках отдельные фирмы учитывают возможную реакцию своих конкурентов до того, как начинают рекламу и предпринимают другие расходы по продвижению товара на рынок. Олигополистическая фирма может существенно увеличить свою долю рынка при помощи рекламы только в том случае, если соперничающие фирмы не нанесут ответного удара, начав свои собственные рекламные кампании. Для того, чтобы лучше понять проблемы, с которыми сталкивается олигополистическая фирма при выборе стратегии маркетинга, полезно подойти к ней с позиции теории игр. Т.е. фирмы должны выработать для себя стратегию максимина, и решить, выгодно им начинать рекламные кампании или нет. Если фирмы не начинают рекламные кампании, то их прибыли не изменяются. Однако, если обе фирмы стремятся избежать наихудшего исхода, проведя стратегию максимина, то они обе предпочитают рекламировать свой товар. Обе гонятся за прибылью и обе в итоге имеют потери. Это происходит потому, что каждая выбирает стратегию с наименьшими потерями. Если бы они договорились не рекламировать, то они получили бы большие прибыли. Есть также доказательства того, что реклама на олигополистических рынках осуществляется в больших маштабах, чем это необходимо для максимизации прибыли. Часто реклама конкурирующих фирм ведет только к повышению издержек, не увеличивая при этом сбыт продукции, т.к. соперничающие фирмы сводят рекламные кампании друг друга на нет. Другие исследования показали, что реклама способствует повышению прибыли. Они указывают на то, что чем выше доля расходов на рекламу по отношению к объему продаж в отрасли, тем выше отраслевая норма прибыли. А т.к. более высокие нормы прибыли указывают на наличие монопольной власти, то это подразумевает, что реклама ведет к большему контролю за ценой. Неясно, однако, обусловливают ли более высокие рекламные расходы более высокие прибыли или более высокие прибыли вызывают большие расходы на рекламу. Другие модели олигополии. Чтобы попытаться объяснить определенные типы делового поведения, разработаны другие модели олигополии. Первая пытается объяснить неизменность цен; вторая -почему фирмы часто следуют за ценовой политикой фирмы, которая выступает как лидер в объявлении изменения цены; третья показывает, каким образом фирмы могут устанавливать цены так, чтобы не максимизировать текущие прибыли, но зато максимизировать прибыль в долгосрочном плане, путем предотвращения появления на рынке новых продавцов. 3. Модель дуополии Курно Дуополия - это рыночная структура, при которой два продавца, защищенные от появления дополнительных продавцов, являются единственными производителями стандартизированной продукции, не имеющей близких заменителей. Экономические модели дуополии полезны, чтобы проиллюстрировать, как предположения отдельного продавца насчет ответа соперника воздействуют на равновесный выпуск Классическая модель дуополии - это модель, сформулированная в 1838 г. французским экономистом Огюстеном Курно. Эта модель допускает, что каждый из двух продавцов предполагает что его конкурент всегда будет удерживать свой выпуск неизменным на текущем уровне. Она также предполагает, что продавцы не узнают о своих ошибках. В действительности предположения продавцов о реакции конкурента, вероятно, поменяются, когда они узнают о своих предыдущих ошибках. Допустим, что в регионе есть только два производителя товара Х. Любому желающему приобрести товар Х приходится приобретать его у одного из этих двух производителей. Товар Х каждой фирмы стандартизирован и не имеет качественных различий. Никакой другой производитель не может войти на рынок. Допустим, что оба производителя могут выпускать товар Х при одинаковых затратах и что средние издержки неизменны и равны, следовательно, предельным издержкам. График А рис. 10, показывает рыночный спрос на товар Х, помеченный Dm, вместе со средними и предельными издержками производства. Если бы товар Х производился на конкурентном рынке, то выпуск был бы Qc ед., а цена была бы Pc=AC=MC. Двумя фирмами, выпускающими товар Х являются фирма А и фирма В. Фирма А начала производить товар Х первая. До того, как фирма В начинает производство, фирма А обладает всем рынком и предполагает, что выпуск соперничающих фирм всегда будет равен нулю. Поскольку она считает, что обладает монополией, то производит монопольный выпуск, соответствующий точке, в которой MRm=MC. Получающаяся в итоге цена равна Pm. Предположим линейную кривую спроса. Это подразумевает, что предельный доход будет падать с ростом выпуска вдвое быстрее цены. Поскольку кривая спроса делит отрезок РсЕ пополам, то монопольный выпуск составляет половину конкурентного выпуска. Следовательно, первоначальный выпуск фирмы А, максимизирующий его прибыль составляет Qm ед. Сразу же после того, как фирма А начинает производство, на рынке появляется фирма В. Появление новых фирм невозможно. Фирма В предполагает, что фирма А не будет отвечать изменением выпуска. Она, следовательно, начинает производство, предполагая, что фирма А будет продолжать выпускать Qm ед. товара Х. Кривая спроса, который фирма В видит для своего товара, показана на гр. В рис. 10. Она может обслужить всех тех покупателей, которые купили бы товар Х, если бы цена упала ниже текущей цены фирмы А, Pm. Следовательно, кривая спроса на ее выпуск начинается при цене Pm, когда рыночный спрос составляет Qm ед. товара. Эта кривая спроса Db1, продажи вдоль этой кривой представляют собой прибавку, обеспечиваемую фирме В к текущему рыночному выпуску Qm ед., которые до этого момента выпускала фирма А. Кривая предельного дохода, соответствующая кривой спроса Db1 - MRb1. Фирма В производит объем продукции, соответствующий равенству MRb1=MC. Судя по отсчету на оси выпуска от точки, в которой выпуск товара Х равен Qm ед., видим, что этот объем составляет 0.5.Х ед. товара. Увеличение рыночного предложения товара Х с Х до 1.5 Х ед., однако, уменьшает цену единицы товара Х с Pm до Р1. В таблице 2 представлены данные выпуска продукции каждой фирмы за первый месяц деятельности. Максимизирующий прибыль выпуск каждой фирмы всегда составляет половину разницы между Qc и тем объемом производства, который, как она предполагает, будет иметь другая фирма. Конкурентный выпуск - это выпуск, соответствующий цене Р =МС - в этом случае 2Х ед. товара. Как показывает таблица фирма А начинает с производства 0.5 Qc, при условии, что выпуск ее соперника равен нулю. Тогда фирма В в этом месяце выпускает 0.5 Х товара Х, что составляет 0.5(0.5Qc)=0.25 Qc. Это половина разности между конкурентным выпуском и монопольным выпуском, который первоначально обеспечивала фирма А. Падение цены товара Х, вызванное дополнительным производством фирмы В, приводит к изменению кривой спроса фирмы А. Фирма А теперь предполагает, что фирма В будет продолжать выпускать 0.5.Х ед. товара. Она видит спрос на свой товар Х как начинающийся в точке кривой рыночного спроса, соответствующей месячному выпуску 0.5. Х ед. Ее спрос теперь равен Da1, как показано на гр. С, рисунок 5. Максимизирующий для нее прибыль выпуск равен теперь половине разности между конкурентным выпуском и тем объемом, который в настоящее время производит фирма В. Это происходит, когда MRa1=MC. Фирма А предполагает, что фирма В будет продолжать выпускать 0.5.Х ед. товара после того, как он отрегулирует свой выпуск, следовательно, максимизирующий прибыль выпуск равен у фирмы А 1/2(2X - 1/2X)=3/4 X . Это можно записать в виде: 1/2(Qc - 1/4Qc)=3/8 Qc, что и показано в таблице 2. Модель дуополии Курно (рис. 10). Первый месяц. Гр. А Цена    Pm Pc E MC=AC  Mrm Dm  Qm=1/2Qc Qc Q Гр. В Цена   Pm  P1  MC=AC MC=ACMRb1 Db1  1/2Qc 3/4 Qc Qc Q Второй месяц. Гр. С  Цена Цена  Р2  МС=АС МС=АСMRa1 Da1  1/4 Qc 5/8 Qc Qc Гр. D    P3 P3 MC=AC  MRb2 Db2  3/8Qc11/16QcQc Окончательное (гр. Е)   Pe  MC=AC MC=ACD  1/3Qc 2/3Qc Qc Дуопольное равновесие Курно - табл. 2  Месяц Вып. фирмы А Вып. фирмы В  1 1/2Qc 1/2(1/2Qc)=1/4Qc 2 1/2(Qc-1/4Qc)=3/8Qc 1/2(Qc-3/8Qc)=5/16Qc 3 1/2(Qc-5/10Qc)=11/32Qc 1/2(Qc-11/32Qc)=21/64Qc 4 1/2(Qc-21/64Qc)=43/128Qc 1/2(Qc-43/128Qc)=85/256Qc Конечное равновесие Qa=(1-(1/2Qc+1/8Qc+1/32Qc+...))Qc=(1-1/2(1-1/4))Qc=1/3Qc Qb=(1/4+1/16+1/64+...)Qc=(1/4(1-1/4))Qc=1/3Qc Общий выпуск =2/3Qc  Теперь очередь фирмы В отвечать снова. Фирма А снизит свое производство С 1/2 Qc до 3/8Qc - это приводит к снижению общего предложения товара Х с 3/4Qc до 5/8Qc. В результате этого цена товара вырастает до Р2. Фирма В предполагает, что фирма А будет продолжать выпускать это количество. Она рассматривает свою кривую спроса как линию, начинающуюся в точке, где рыночный выпуск равен 3/8Qc.Эта кривая спросаDb2, указанная на гр.D, рис.10. Максимальная прибыль существует в той точке, где MRb2=MC. Это равняется половине разности между конкурентным выпуском и величиной в 3/8 конкурентного выпуска, которую в настоящее время поставляет фирма А. Как показано в таблице 2, фирма В теперь производит 5/16 конкурентного выпуска. Общий рыночный выпуск равен теперь 11/16Qc, а цена снижается до Р3. За каждый месяц каждый дуополист производит половину разности между конкурентным выпуском и выпуском, осуществляемым конкурентной фирмой. Как показано на гр. Е, рис.10, каждая фирма выпускает 1/3 Qc, а цена равна Ре. Это равновесие Курно для дуополии. Оно существовало бы. если только каждая фирма упорно полагала бы, что другая не будет регулировать свой выпуск, что подразумевает, что управление фирмы не учитывает своих ошибок, что, конечно, является большим упрощением. Но при более сложных допущениях становится сложно определить условия равновесия. Пример Z. Отраслевой спрос на продукцию характеризуется функцией Р = 100 - 0.5Q; в отрасли работают две максимизирующие прибыль фирмы А и В со следующими функциями затрат: ТСа = 20 + 0.75qa^2 и ТСь = 30 + 0.5qb^2. Выведем уравнение реакции для фирмы А. Так как MRa = 100 - qa - 0.5qь и MCa = 1.5qa, то a = max при 100 - qa - 0.5qb = 1.5 qa qa = 40 - 0.2qb. Аналогичные расчеты для фирмы В дают ее уравнение реакции: qb = 50 - 0.25qa. Равновесные значения цены и объемов предложения определяются из следующей системы уравнений: P = 100 - 0.5 (qa + qb), q  a = 40 - 0.2 qb, qA* = 31.6, qb* = 42.1, P* = 63.2. a = 40 - 0.2 qb, qA* = 31.6, qb* = 42.1, P* = 63.2. qb = 50 - 0.25qa. В состоянии равновесия прибыли фирм соответственно равны: a = 63.2 • 31.6 - 20 - 0.75 * 31.6^2 == 1228.2, ь = 63.2*42.1 - 30 - 0.5*42.1^2 = 1744.5. Чтобы проследить за процессом установления равновесной цены в модели дуополии Курно, допустим, что сначала в отрасли работала только фирма А. Она установила монопольную цену Рм = 80 и выпускает qm= 40. Для фирмы В, решившей в такой ситуации войти в отрасль, функция спроса имеет вид Р = 100 - 0.5(40 + qb), а ее предельный доход определяется по формуле MRb = 80- qb. Прибыль фирмы В будет максимальной, если 80 - qь = qb, т. е. при выпуске 40 ед. продукции. Такой же результат получается из уравнения реакции фирмы В. Вследствие этого рыночная цена снизится до 60 ден. ед. При такой цене объем предложения фирмы А уже не обеспечивает ей максимальную прибыль, и она изменит объем выпуска в соответствии со своим уравнением реакции исходя из того, что фирма В выпускает 40 ед. продукции: q’a = 40 - 0.2*40 = 32. В результате цена возрастет до 64. Ответный ход фирмы В выразится в том, что она в соответствии со своим уравнением реакции предложит на рынок q’b = 50 - 0.25 • 32 = 42, сбивая тем самым цену до 63. После того как фирма А в очередной раз скорректирует свой выпуск, qa’' = 40 - 0.2 * 42 = 31.6, в отрасли установится равновесная цена 63.2. Обобщение модели Курно. Используя предпосылки модели дуополии Курно, можно построить модель ценообразования при любом числе конкурентов. Примем в целях упрощения, что у всех конкурентов одинаковые экономические затраты на единицу продукции: ACi = 1 = const; i = 1, .., n. Тогда прибыль i-той фирмы равна i, = Pqi, -lqi; так как Р =g - h qi , то прибыль i-той фирмы можно представить в виде i = [g - h(q1 + q2 + ... + qn)] qi - lqi = gqi - hqiq1 - hqiq2 - ... - hqi^2 - ... - hqiqn - lqi. Она достигает максимума при i / qi = g - hq1 - hq2 - ... - 2hqi - ... - hqn - l = g - hq1 - hq2 - ... - hqi - ... - hqn - hqi - l = 0 Поскольку g -hq1 -hq2 -...-hqn =P, то условие максимизации прибыли для отдельной фирмы имеет вид Р -hqi = 1. (4.25) Из равенства (4.25) следует qi* = (P-l)/h, т. е. в состоянии равновесия все фирмы будут иметь одинаковый объем реализации: qi = nqi = Q, или qi = Q / n = (g - P) / nh (4.26) Это вытекает из допущения, что у всех фирм одинаковые предельные затраты производства. Подставив значение (4.26) в уравнение (4.25), получим значение равновесной цены как функции от числа одинаковых по размеру фирм: P* = l + hqi = l + h ((g - P*) / nh) P* = (nl + g) / (n + 1) При n = 1 получаем монопольную цену, a по мере увеличения п цена приближается к предельным издержкам. 4. Модель Штакельберга. Равновесие в модели Курно достигается за счет того, что каждый из конкурентов меняет свой объем выпуска в ответ на изменение выпуска другого до тех пор, пока такие изменения увеличивают их прибыль. В модели Штакельберга предполагается, что один из дуополистов выступает в роли лидера, а другой — в роли аутсайдера. Лидер всегда первым принимает решение об объеме своего выпуска, а аутсайдер воспринимает выпуск лидера в качестве экзогенного параметра. В этом случае равновесные объемы выпуска определяются не в результате решения системы уравнений реакции дуополистов, а на основе максимизации прибыли лидера, в формуле которой вместо выпуска аутсайдера находится уравнение его реакции. Определим равновесие Штакельберга в условиях примера Z. Если лидером является фирма А, то ее выпуск определяется из равенства MRa = МСа. Общая выручка фирмы А с учетом уравнения реакции фирмы В равна: TRa = =Pqa = [100 - 0.5(qa + 50 - 0.25qa)]qa = 75qa - 0.375 qa^2; тогда MRa = 75 - 0.75qa. Следовательно, прибыль фирмы А будет максимальной при 75 - 0.75qa = 1.5qa. Отсюда qa = 33.33; qь = 50 - 0.25 * 33.33 = 41.66; P = 100 - 0.5(33.33 + 41.66) = 62.5; a = 62.5 * 33.3 - 20 - 0.75*33.3^2 = 1230; b = 62.5*41.7 - 30 - 0.5 * 41.7^2 = 1707. 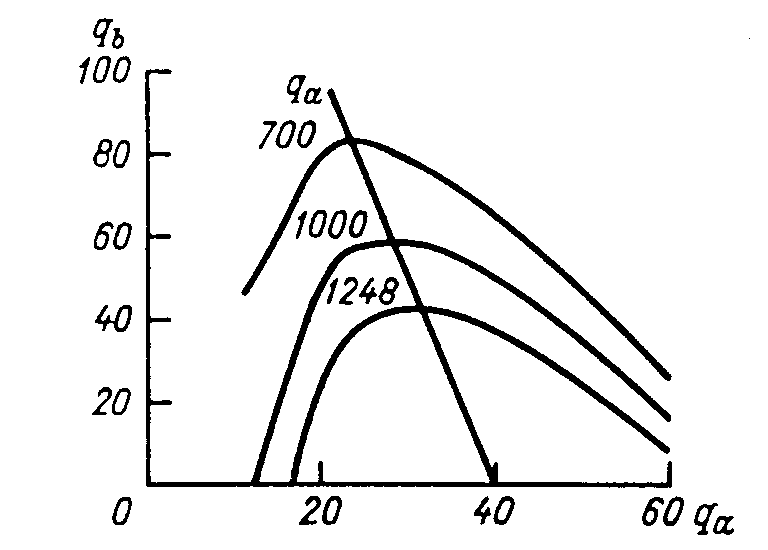 Рис. 11 Линия реакции и изопрофиты Таким образом, в результате пассивного поведения фирмы В ее прибыль снизилась, а фирмы А возросла. Если бы фирмы поменялись ролями, то прибыль фирмы А равнялась бы 1189, а фирмы В — 1747.8. Для наглядного сопоставления равновесия Курно с равновесием Штакельберга линии реакции дуополистов нужно дополнить линиями равной прибыли (изопрофитами). Уравнение изопрофиты образуется в результате решения уравнения прибыли дуополии относительно ее выпуска при заданной величине прибыли. По данным примера 4.7 на рис. 4.32 построены изопрофиты и линия реакции фирмы А. Чем ниже расположена изопрофита, тем большему размеру прибыли она соответствует, так как ее приближение к оси абсцисс соответствует росту qa и уменьшению qb. Наложив на рис. 11 аналогичный рисунок для фирмы В, получим рис. 12, на котором равновесие Курно отмечено точкой С, а равновесие Штакельберга точкой Sa при лидерстве фирмы А и точкой Sb при лидерстве фирмы В. Картель. Однако наибольшие прибыли олигополисты получат в случае организации картеля — явного или скрытого сговора о распределении объема выпуска с целью поддержания монопольной цены на данном рынке. В условиях рассматриваемого числового примера суммарная прибыль участников картеля определяется по формуле = [100 - 0.5(qA +qB)] (qA+qB) - 20 - 0.75qA^2 - 30 - 0.5qB^2 = 100qA + 100qB -qAqB- - 1.25qA^2 - qB^2 - 50. 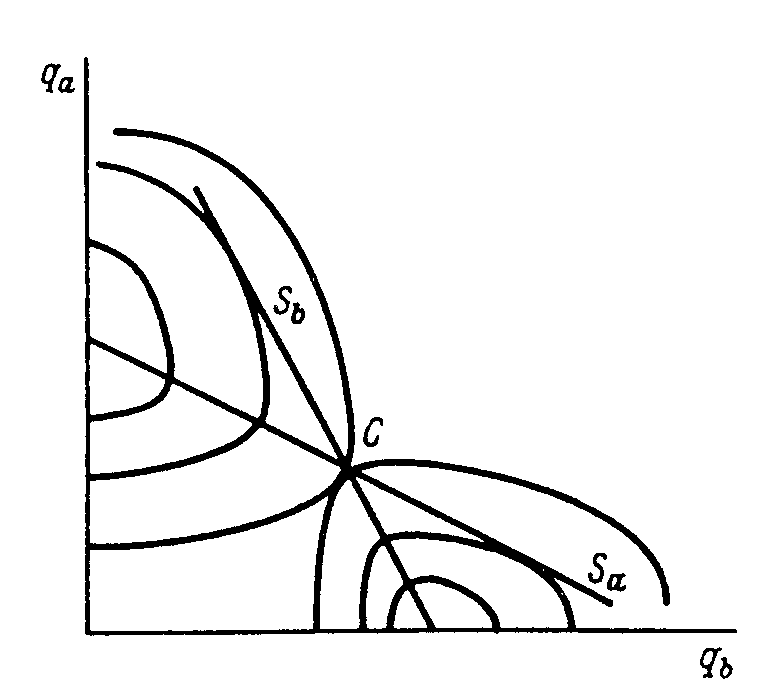 Рис. 12. Равновесие Курно и равновесие Штакельберга. Условием ее максимизации является система уравнений: 100 - qB- 2.5qA= 0, 100 - qA - 2qB = 0, из которой следует, что фирма А должна производить 25, а фирма В — 37.5 ед. продукции. В этом случае рыночная цена будет равна Р = 100 - 0.5(25 + 37.5) = 68.75, а прибыли фирм А и В соответственно равны A = 68.75 * 25 - 20 - 0.75*25^2 = 1230, B = 68.75 * 37.5 - 30 - 0.5 * 37.5^2 = 1845. В таблице 3. показано, как меняется величина прибыли дуополистов в зависимости от рассмотренных вариантов их поведения на рынке. Таблица 3.
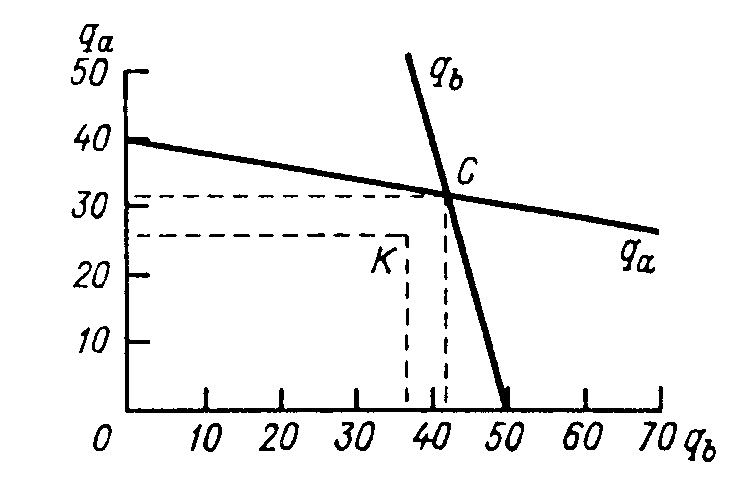 Рис. 13. Выпуск дуополий при равновесии по Курно и образовании картеля В графическом виде результат решения рассматриваемого примера представлен на рис. 13. Точка С на пересечении линий реакции фирм А и В определяет их выпуск в состоянии равновесия по Курно, а точка К — при образовании картеля. При пассивном поведении фирмы В точка, представляющая объемы выпуска каждой из фирм, находится на линии реакции фирмы В, левее точки С; при пассивном поведении фирмы А эта точка расположена на линии реакции фирмы А, правее точки С. В рассматриваемом примере создание картеля обеспечивает фирме В на 97 ед. прибыли больше, чем при самом благоприятном для нее варианте конкуренции, т. е. при пассивном приспособлении выпуска фирмы А к ее выпуску. Часть этого приращения прибыли фирма В может передать фирме А за согласие придерживаться картельной цены. 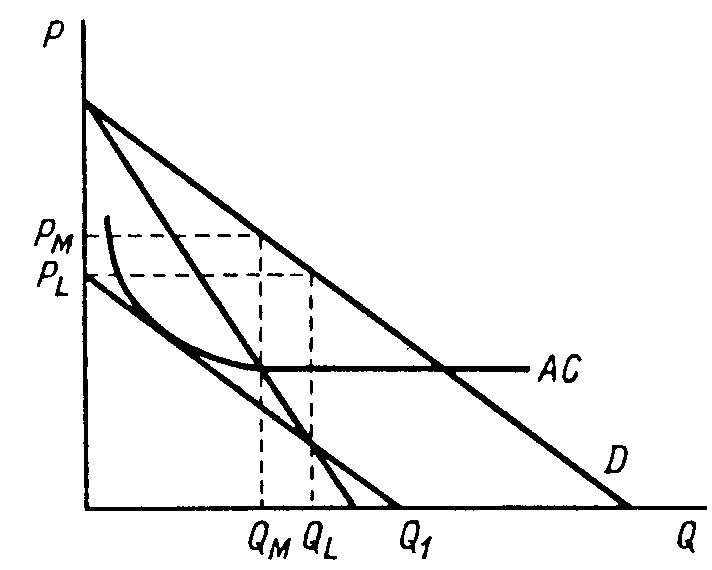 Рис. 14. Определение лимитной цены. Монопольная цена, обеспечивая картелю избыточную прибыль, стимулирует приток в отрасль новых конкурентов. Чтобы предотвратить появление новых производителей данной продукции, картель может установить лимитную цену (pl), не позволяющую новым фирмам получить прибыль. Графический способ определения лимитной цены показан на рис. 14. Кривая АС представляет средние затраты на выпуск всех участников картельного соглашения. Для предотвращения появления новых конкурентов вместо сочетания Рм,0м, соответствующего точке Курно, нужно выбрать комбинацию pl,ql. Тогда остаточный (неудовлетворенный) спрос на данном рынке будет представлен отрезком pl,Q1, который целиком расположен ниже кривой средних затрат. Поэтому если потенциальные конкуренты имеют одинаковую с членами картеля технологию, то производить данное благо им не выгодно. Выведем формулу лимитной цены. Пусть АС = l + k/Q. Прямая отраслевого спроса D построена по формуле цены спроса: Р =g— hQ. Соответственно прямая остаточного спроса при цене pl описывается формулой Рос = pl- hQ. В точке касания кривой средних затрат АС и прямой остаточного спроса PL,Q1 выполняется равенство PL - hQ = l + k / Q (4.24) и наклоны обеих линий одинаковы. Значит, dPoc / dQ = dAC / dQ, т.е. -h = -k/Q^ 2 Q = (k / h)^1/2. Следовательно, точка касания линий АС и Рос соответствует Q = (k / h)^1/2. Подставив это значение Q в равенство (4.24), получим формулу для определения лимитной цены: PL = l + k / Q + h (k / h)^1/2 = l + 2(k / h)^ 1/2 5. Кривые реагирования. То же самое равновесие можно изобразить и другим способом. Кривые реагирования показывают максимизирующие прибыль размеры выпуска, который будет осуществляться одной фирмой, если даны размеры другой фирмы-соперника. Кривая реагирования 1 представляет выпуск фирмы В как функцию от выпуска фирмы А, а кривая реагирования 2 - наоборот. Q  a a Qc QcЛиния реагирования 1 1/2Qc 3     /8Qc /8Qc 1/3Qc Линия реагирования 2 1/4Qc  Qb Qb 1/4Qc1/3Qc 1/2Qc Qc Любой выпуск выше Qc невыгоден, т.к. цена падает ниже уровня средних издержек. Следовательно, если выпуск одной из фирм равен Qc ед., то вторая отвечает нулевым выпуском. Равновесие достигается, когда две кривые реагирования пересекаются и каждая фирма выпускает 1/3Qc. При любом другом выпуске фирмы взаимно реагируют на выбор друг другом величины выпуска. ЗАКЛЮЧЕНИЕ Помимо факторов, определяющих рыночный спрос и рыночное предложение, уровень равновесной цены зависит от характеристик рынка, на котором осуществляются торговые сделки. Характеристики рынка формируются как условиями его функционирования ( открытый—закрытый, организованный—стихийный и пр.), так и объектами совершаемых на нем сделок (недвижимость, услуги, патенты, облигации и пр.). Совокупность нескольких характеристик рынка образует его структуру, или тип. Путем сочетания различных свойств рынка можно составить большое число рыночных структур, но наиболее распространенными из них на рынке благ являются олигополия, совершенная конкуренция, монополия и монополистическая конкуренция. В условиях олигополии специфическим фактором ценообразования является многовариантный стратегический план реакции производителя на ожидаемые действия немногочисленных конкурентов. Из-за неоднозначности ответных реакций олигополистов не существует единой теории олигопольного ценообразования. Но в любом случае цена на рынке олигополии предложения при прочих равных условиях превышает цену, складывающуюся на рынке совершенной или монополистической конкуренции, и ниже монопольной цены. | ||||||||||||||||||||
