Основы системного анализа. 1. Понятие Системного анализа
 Скачать 482.81 Kb.
|
|
Если оправданы лишь качественные оценки объектов по тем или иным качественным признакам, то используются методы ранжирования, парного и множественного сравнения. Если характер анализируемой информации таков, что целесообразно получить численные оценки объектов то используют методы численной оценки от непосредственных численных оценок до более тонких методов Черчмена-Акоффа и Неймана –Моргенштерна. В дальнейшем будем предполагать, что имеется конечное число измеряемых или оцениваемых альтернатив (объектов) и сформулированы один или несколько признаков сравнения, по которым осуществляет сравнение свойств объектов. Следовательно, методы измерения будут различаться лишь процедурой обработки результатов сравнения свойств объектов. Эта процедура включает построение отношений между объектами эмпирической системы, выбор преобразования и определение типа шкалы измерения. 21. Ранжирование Метод представляет собой процедуру упорядочения объектов, выполняемую экспертом. На основе знаний и опыта эксперт располагает объекты в порядке предпочтения, руководствуясь одним или несколькими выбранными показателями сравнения. В зависимости от вида отношений между объектами возможны различные варианты упорядочения объектов. 1) Пусть среди объектов нет одинаковых по сравниваемым показателям, то есть нет эквивалентных объектов. В этом случае между объектами существует только отношение строгого порядка. В результате сравнения всех объектов по отношению строгого порядка составляется упорядоченная последовательность , где объект с первым номером является наиболее предпочтительным из всех объектов, объект со вторым номером менее предпочтителен, чем первый объект, но предпочтительней всех остальных объектов и т.д. Полученная система объектов с отношением строгого порядка при условии сравнимости всех объектов по этому отношению образует полный строгий порядок. Для этого отношения доказано существование числовой системы, элементами которой являются действительные числа, связанные между собой отношением неравенства «>». Это означает, что упорядочению объектов соответствует упорядочение чисел, где возможна и обратная последовательность, в которой более предпочтительному объекту приписывается наименьшее число, и по мере убывания предпочтения объектам приписываются большие числа. Соответствие последовательностей, то есть их гомоморфизм, можно осуществить, выбирая любые числовые представления. Единственным ограничением является монотонность преобразования. Следовательно, допустимое преобразование при переходе от одного числового представления к другому должно обладать свойством монотонности. Таким свойством допустимого преобразования обладает шкала порядков, поэтому ранжирование объектов есть измерение на порядковой шкале. Рассмотрим понятие шкалы порядка. Шкала называется шкалой порядка или иначе ранговой шкалой, если множество допустимых преобразований состоит из всех монотонно возрастающих допустимых преобразований шкальной системы. Где X – эмпирическая система с отношением, Y – знаковая система с отношением, являющаяся отображением X. В практике ранжирования чаще всего применяется числовое представление последовательности в виде натуральных чисел: x1=ϕ(a1)=1,x2=ϕ(a2),...,xN=ϕ(aN)=N, т.е. используется числовая последовательность. Числа называются рангами и обычно обозначаются буквами r1,r2,...,rNr1,r2,...,rN. 2) Применение строгих численных отношений больше, меньше или равно не всегда позволяет установить порядок между объектами. Поэтому наряду с ними используются отношения для определения большей или меньшей степени какого-то качественного признака (отношения частичного порядка, например – полезности) используются отношения типа «более предпочтительно» (≻), «менее предпочтительно» (≺), «равноценно» (≈) или «безразлично» (∼). Упорядочение объектов при этом может иметь следующий вид: a1≻a2≻a3≈a4≈a5≻a6≻a7...≻an−1≈an Такое упорядочение образует нестрогий линейный порядок. Для отношения нестрогого линейного порядка доказано существование числовой системы с отношениями неравенства и равенства между числами, описывающими свойства объектов. Любые две числовые системы для нестрогого линейного порядка связаны между собой монотонным преобразованием. Следовательно, ранжирование при условии наличия эквивалентных объектов также представляет собой измерение на порядковой шкале. В практике ранжирования объектов, между которыми допускаются отношения как строгого порядка, так и эквивалентности, числовое представление выбирается следующим образом. Наиболее предпочтительному объекту присваивается ранг, равный единице, второму по предпочтительности – ранг, равный двум, и т.д. Для эквивалентных объектов удобно с точки зрения технологии последующей обработки экспертных оценок назначать одинаковые ранги, равные среднеарифметическому значению рангов, присваиваемых одинаковым объектам. Такие ранги называют связанными рангами. Для приведенного примера упорядочения на основе нестрогого линейного порядка при N=10 имеем: a1≻a2≻a3≈a4≈a5≻a6≻a7...≻a9≈an Ранги объектов a3, a4, a5 в данном случае равны 4 r3=r4=r5= 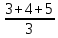 =4В этом же примере ранги объектов a9,a10 также одинаковы и равны среднеарифметическому r9=r10= 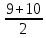 =9,5. Связанные ранги могут оказаться дробными числами. Удобство использования связанных рангов заключается в том, что сумма рангов N объектов равна сумме натуральных чисел от единицы до N. При этом любые комбинации связанных рангов не изменяют эту сумму. Данное обстоятельство существенно упрощает обработку результатов ранжирования при групповой экспертной оценке.При групповом ранжировании каждый S-й эксперт присваивает каждому i-му объекту ранг riS. В результате проведения экспертизы получается матрица рангов [riS] размерности N×k , где k – число экспертов; N – число объектов; . Результаты группового экспертного ранжирования удобно представить в виде таблицы 1: Таблица 1 – Табличное представление результатов группового ранжирования 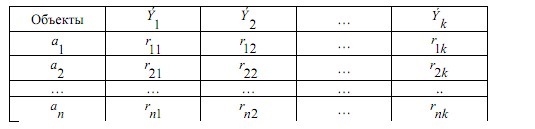 Аналогичный вид имеет таблица, в том случае если осуществляется ранжирование объектов одним экспертом по нескольким показателям сравнения. При этом в таблице вместо экспертов в соответствующих графах указываются показатели. Необходимо помнить, что ранги объектов определяют только порядок расположения объектов по показателям сравнения. Ранги, как числа не дают возможности сделать вывод о том, на сколько или во сколько раз предпочтительнее один объект по сравнению с другим. Если, например, ранг объекта равен трем, то отсюда не следует делать вывод о том, что этот объект в три раза более предпочтителен, чем объект, имеющий ранг, равный единице. Достоинство ранжирования как метода экспертного измерения – простота осуществления процедур, не требующая трудоемкого обучения экспертов. Недостатком ранжирования является практическая невозможность упорядочения большого числа объектов. Как показывает опыт, при числе объектов большем 10-15, эксперты затрудняются в построении ранжировки. Это объясняется тем, что в процессе ранжирования эксперт должен установить взаимосвязь между всеми объектами, рассматривая их как единую совокупность. При увеличении числа объектов количество связей между ними растет пропорционально квадрату числа объектов. Сохранение в памяти и анализ большой совокупности взаимосвязей между объектами ограничиваются психологическими возможностями человека. Психологи утверждают, что оперативная память человека позволяет оперировать в среднем не более чем 7+2 объектами одновременно. Поэтому при ранжировании большого числа объектов эксперты могут допускать существенные ошибки. 22. Парное сравнение. Этот метод представляет собой процедуру установления предпочтения объектов при сравнении всех возможных пар. В отличие от ранжирования, в котором осуществляется упорядочение всех объектов, парное сравнение объектов является более простой задачей. При сравнении пары объектов, возможно, либо отношение строгого порядка, либо отношение эквивалентности. Из этого следует, что парное сравнение, так же, как и ранжирование, есть измерение на порядковой шкале. В результате сравнения пары объектов эксперт упорядочивает ее, высказывая либо, либо, либо. Выбор числового представления можно произвести так: если, то; если предпочтение в паре обратное, то знак неравенства меняется. Наконец, если объекты эквивалентны, то. В практике парного сравнения используются следующие числовые представления: 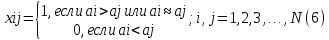 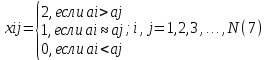 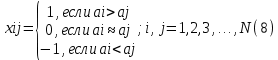 Результаты сравнения всех пар объектов удобно представить в виде матрицы. Пусть, например, имеются пять пар объектов и проведено парное сравнение этих объектов по предпочтительности. Результатысравненияпредставленыввиде: a1≻a2,a1≻a3,a1≻a4,a1≻a5,a2≻a3,a2≻a4,a4≻a5,a2≻a5a3≈a4,a3≺a5 (9) Используя числовое представление (6), составим матрицу измерения результатов парных мнений (таблица 2). Таблица 2 – табличное представление сравнения (9) по правилу (6) 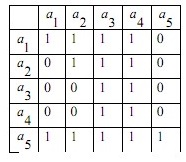 В таблице 2 на диагонали всегда будут расположены единицы, поскольку каждый объект эквивалентен сам себе. Представление (7) характерно для отображения результатов спортивных состязаний. За выигрыш даются два очка, за ничью – одно и за проигрыш – ноль очков. Предпочтительность одного объекта перед другим трактуется в данном случае как выигрыш одного участника турнира у другого. Таблица результатов измерения при использовании числового представления не отличается от таблиц результатов спортивных турниров за исключением диагональных элементов (обычно в турнирных таблицах диагональные элементы заштрихованы). В качестве примера в таблице 3 приведены результаты измерения пяти объектов с использованием представления (7), соответствующие таблице 1. Если сравнение пар объектов производится отдельно по различным показателям или сравнение осуществляет группа экспертов, то по каждому показателю или эксперту составляется своя таблица результатов парных сравнений. Сравнение во всех возможных парах не дает полного упорядочения объектов, поэтому возникает задача ранжирования объектов по результатам их парного сравнения. Таблица 3 – Табличное представление сравнения (9) по правилу (7) 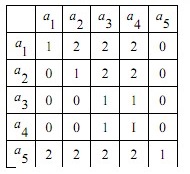 Однако, как показывает опыт, эксперт далеко не всегда последователен в своих предпочтениях. В результате использования метода парных сравнений эксперт может указать, что объект a1предпочтительнее объекта a2, a2 предпочтительнее объекта a3 и в то же время a3 предпочтительнее объекта a1. Такая непоследовательность эксперта может объясняться различными причинами: сложность задачи, неочевидность предпочтительности объектов или разбиения их на классы, недостаточной компетентностью эксперта недостаточно четкой постановкой задачи, многокритериальностью рассматриваемых объектов и т.д. Непоследовательность эксперта приводит к тому, что в результате парных сравнений при определении сравнительной предпочтительности объектов мы не получаем ранжирования и даже отношений частного порядка – не выполняется свойство транзитивности. 23. Множественные сравнения. Непосредственная оценка Множественные сравнения отличаются от парных сравнений тем, что экспертам последовательно предъявляются не пары, а тройки, четверки, …, n-ки (n<N) объектов. Эксперт их упорядочивает по важности или разбивает на классы в зависимости от целей экспертизы. Множественные сравнения занимают промежуточное положение между парными сравнениями и ранжированием. С одной стороны, они позволяют использовать больший, чем при парных сравнениях, объем информации для определения экспертного суждения в результате одновременного соотнесения объекта не с одним, а с большим числом объектов. С другой стороны, при ранжировании объектов их может оказаться слишком много, что затрудняет работу эксперта и сказывается на качестве результатов экспертизы. В этом случае множественные сравнения позволяют уменьшить до разумных пределов объем поступающей к эксперту информации. Непосредственная оценка. Метод непосредственной оценки заключается в присваивании объектам числовых значений на шкале интервалов. Эксперту необходимо поставить в соответствие каждому объекту точку на определенном отрезке числовой оси. При этом необходимо, чтобы эквивалентным объектам приписывались одинаковые числа. Тип шкал интервалов содержит шкалы, единственные с точностью до множества положительных линейных допустимых преобразований. Измерения на шкале интервалов могут быть достаточно точными при полной информированности экспертов о свойствах объектов. Эти условия на практике встречаются редко, поэтому для измерения применяют бальную оценку. При этом вместо непрерывного отрезка числовой оси рассматриваются участки, которым приписываются баллы. Эксперт приписывает объекту балл, тем самым измеряет его с точностью до отрезка числовой оси. Применяются 5-ти, 10-ти и 100 бальные шкалы. 24. Последовательное сравнение (метод Черчмена Акоффа). Этот метод относится к числу наиболее популярных при оценке альтернатив. В нем предполагается последовательная корректировка оценок, указанных экспертами. Основные предположения, на которых основан метод, состоят в следующем: каждой альтернативе ai,(i=1,...,n) ставится в соответствие действительное неотрицательное число ϕ(ai); если альтернатива ai≻aj, то ϕ(ai)>ϕ(aj), если же ai≈aj, то ϕ(ai)=ϕ(aj); если ϕ(ai) и ϕ(aj) – оценки альтернатив ai и aj, то сумма ϕ(ai)+ϕ(aj) соответствует совместному осуществлению альтернатив ai и aj Наиболее сильным является последнее предположение об аддитивности оценок альтернатив. Согласно методу Черчмена-Акоффа альтернативы ранжируются по предпочтительности. Пусть альтернатива a1 наиболее предпочтительна, за ней следует a2 и т.д. Эксперт указывает предварительные численные оценки ϕ(ai) для каждой из альтернатив. Иногда наиболее предпочтительной альтернативе приписывается оценка 1, остальные оценки располагаются между 0 и 1 в соответствии с их предпочтительностью. Затем эксперт производит сравнение альтернативы a1, и суммы альтернатив a2,...,aN. Если a1 предпочтительнее, то эксперт корректирует оценки так, чтобы 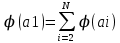 После того как альтернатива a1 оказывается предпочтительней суммы альтернатив a2,...,ak(k>2), она исключается из рассмотрения, а вместо оценки альтернативы a1 рассматривается и корректируется оценка альтернативы a2. Процесс продолжается до тех пор, пока откорректированными не окажутся оценки всех альтернатив. При достаточно большом N применение метода Черчмена-Акоффа становится трудоемким. В этом случае целесообразно разбить альтернативы на группы, а одну из альтернатив, например максимальную, включить во все группы. Это позволяет получить численные оценки всех альтернатив с помощью оценивания внутри каждой группы. Данный метод считается одним из самых эффективных. 25. Методы Неймана-Моргенштерна и согласования оценок. Метод Неймана-Моргенштерна заключается в получении численных оценок альтернатив с помощью, так называемых, вероятностных смесей. В основе метода лежит предположение, согласно которому эксперт для любой альтернативы aj менее предпочтительной, чем ai, но более предпочтительной чем a1(a1≺aj≺ai) может указать число ap(0≤p≤1) такое, что альтернатива aj эквивалентна смешанной альтернативе (вероятностной смеси) [pai(1−p)a1]. Смешанная альтернатива состоит в том, что альтернатива ai, выбирается с вероятностью p, а альтернатива a1 - с вероятностью 1−p. Очевидно, что если p достаточно близко к 1, то альтернатива aj менее предпочтительна, чем смешанная альтернатива [pai,(1−p)a1]. Если указанная система предпочтений выполнена, то для каждой из набора основных альтернатив a1,a2,...,aN определяются числа x1,x2,...,xN характеризующие численную оценку смешанных альтернатив. Численная оценка смешанной альтернативы [p1a1,p2a2,...,pNaN] равна: p1x1=p2x2+...+pNxN Таким образом, устанавливается существование функции полезности, значение которой характеризует степень предпочтительности любой смешанной альтернативы. Более предпочтительна та смешанная альтернатива, для которой значение функции полезности больше. Метод согласования оценок Этот метод обычно применяется при обработке индивидуальных экспертных оценок. Метод имеет много вариантов, различающихся способами, при помощи которых из индивидуальных оценок получается обобщенная. При этом используют различные методы согласования оценок: 1) Простейшие, основанные на получении средней вероятности, 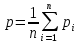 или средневзвешенного значения вероятности 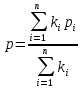 Где ki – веса, приписываемые оценке каждого эксперта; 2) Специальные методы оценки измерения и повышения коэффициентов согласованности (или коэффициентов непротиворечивости) мнений экспертов; 3) Методы, основанные на отборе экспертной группы с высоким коэффициентом согласованности мнений. Наиболее часто при обработке материалов коллективной экспертной оценки используются методы теории ранговой корреляции. Для количественной оценки степени согласованности мнений экспертов применяется коэффициент конкордации W, который позволяет оценить, насколько согласованы между собой ряды предпочтительности, построенные каждым экспертом. Его значение находится в пределах. – полную противоположность, полное совпадение ранжировок. Практически достоверность считается хорошей, если. Небольшое значение коэффициента конкордации, свидетельствующее о слабой согласованности мнений экспертов, является следствием следующих причин: в рассматриваемой совокупности экспертов действительно отсутствует общность мнений; внутри рассматриваемой совокупности экспертов существуют группы с высокой согласованностью мнений, однако обобщенные мнения таких групп противоположны. Для наглядности представления о степени согласованности мнений двух любых экспертов A и B служит коэффициент парной ранговой корреляции p, он принимает значения от -1 до +1. Значение соответствует полному совпадению оценок в рангах двух экспертов (полная согласованность мнений двух экспертов), а p=−1 – двум взаимно противоположным ранжировкам важности свойств (мнение одного эксперта противоположно мнение другого). Рассмотренные выше методы экспертных оценок обладают различными качествами, но приводят в общем случае к близким результатам. Практика применения этих методов показала, что наиболее эффективно комплексное применение различных методов для решения одной и той же задачи. Сравнительный анализ результатов повышает обоснованность выводов. При этом следует учитывать, что методом, требующим минимальных затрат, является ранжирование, а наиболее трудоемким – метод последовательного сравнения (Черчмена-Акоффа). Метод парного сравнения без дополнительной обработки не дает полного упорядочения объектов. |