ответы к экзамену. Ответы к экзамену. 1 Понятие вероятности. Статистическая вероятность. Свойства вероятности
 Скачать 4.43 Mb.
|
|
1 Понятие вероятности. Статистическая вероятность. Свойства вероятности. Появление события А обладает какой-то степенью возможности, которую можно измерить численно. Это число называется вероятностью события. Наиболее просто вероятности определяются в классической схеме, когда можно выделить полную группу несовместных и равновозможных событий и считать ее пространством элементарных событий. Равновозможность возникает обычно из-за симметрии в опыте (симметричная монета, хорошо перемешанная колода карт, правильная игральная кость, отсутствие оснований предпочесть один результат эксперимента другому). Эксперимент описывается классической вероятностной схемой (моделью), если пространство его элементарных событий состоит из конечного числа равновозможных исходов Q = {ώ1 ώ2,..., ώn}. Тогда вероятность любого элементарного исхода равна 1/n, и потому, если событие А происходит при осуществлении каких-то т исходов, то Р(А) = m/n Таким образом, ВЕРОЯТНОСТЬЮ события А называется отношение числа исходов, благоприятствующих осуществлению этого события к общему числу всех равновозможных и несовместных исходов. Согласно такому определению подсчет вероятности события сводится к подсчету общего числа равновозможных исходов и числа исходов, благоприятствующих наступлению события A. (чаще используются комбинаторные формулы. Свойства вероятности  О ≤ Р( А) ≤ 1, т.к. Р(А) = m/n, и т ≥ 0,п > 0, т ≤ п . Р(Ω) = 1, т.к. т=п. Р(Ѳ) =0,т.к. 0/n= 0. Р(А+ В) = Р(А) + Р(B), если AB = Ѳ (события несовместны). Основной недостаток статистического определения вероятности состоит в необходимости проведения большого числа опытов для вычисления вероятности в соответствии с этим определением. 2 Алгебра событий. 1. Суммой А+В двух событий А и В называют событие, состоящее в том, что произошло хотя бы одно из событий А и В. Суммой нескольких событий, соответственно, называется событие, заключающееся в том, что произошло хотя бы одно из этих событий. Назовем все возможные результаты данного опыта его исходами и предположим, что множество этих исходов, при которых происходит событие А (исходов, благоприятных событию А), можно представить в виде некоторой области на плоскости. Тогда множество исходов, при которых произойдет событие А+В, является объединением множеств исходов, благоприятных событиям А или В 2. Произведением АВ событий А и В называется событие, состоящее в том, что произошло и событие А, и событие В. Аналогично произведением нескольких событий называется событие, заключающееся в том, что произошли все эти события. Геометрической иллюстрацией множества исходов опыта, благоприятных появлению произведения событий А и В, является пересечение областей, соответствующих исходам, благоприятным А и В. 3. Разностью А\B событий А и В называется событие, состоящее в том, что А произошло, а В – нет. Введем еще несколько категорий событий. 4. События А и В называются совместными, если они могут произойти оба в результате одного опыта. В противном случае (то есть если они не могут произойти одновременно) события называются несовместными. Замечание 1. Если изобразить графически области исходов опыта, благоприятных несовместным событиям, то они не будут иметь общих точек. Замечание 2. Из определения несовместных событий следует, что их произведение является невозможным событием. 5. Говорят, что события А1, А2,…,Ап образуют полную группу, если в результате опыта обязательно произойдет хотя бы одно из событий этой группы. Замечание. В частности, если события, образующие полную группу, попарно несовместны, то в результате опыта произойдет одно и только одно из них. Такие события называют элементарными событиями. 6. События называются равновозможными, если нет оснований считать, что одно из них является более возможным, чем другое. 3 Дискретная и непрерывная вероятностные схемы. Случайная величина называется дискретной, если она принимает отдельные, изолированные возможные значения с определенными вероятностями. Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток. Дискретные случайные величины. Для задания дискретной случайной величины нужно знать ее возможные значения и вероятности, с которыми принимаются эти значения. Соответствие между ними называется законом распределения случайной величины. Он может иметь вид таблицы, формулы или графика. Таблица, в которой перечислены возможные значения дискретной случайной величины и соответствующие им вероятности, называется рядом распределения:
Примеры дискретных схем: Бернулли, биноминальная схема, схема Пуассона Случайная величина называется непрерывной, если множество ее возможных значений целиком заполняет некоторый конечный или бесконечный промежуток. Функция f(x), называемая плотностью распределения непрерывной случайной величины, определяется по формуле: f (x) = F′(x), то есть является производной функции распределения. Свойства плотности распределения. f(x) ≥ 0, так как функция распределения является неубывающей. 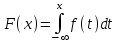 , что следует из определения плотности распределения.Вероятность попадания случайной величины в интервал (а, b) определяется формулой 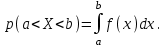 Примеры непрерывных схем: нормальное распределение, экспоненциальное, равномерное 4 Классический подход (перестановка, размещение, сочетание) при вычислении вероятностей При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. Определим основные такие комбинации. 1. Перестановки– это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок Рп = п! 2.Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений  3.Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний  5 Геометрический подход при вычислении вероятностей Геометрическая вероятность Одним из недостатков классического определения вероятности является то, что оно неприменимо к испытаниям с бесконечным количеством исходов. В таких случаях можно воспользоваться понятием геометрической вероятности. Пусть на отрезок L наудачу брошена точка. Это означает, что точка обязательно попадет на отрезок L и с равной возможностью может совпасть с любой точкой этого отрезка. При этом вероятность попадания точки на любую часть отрезка Lне зависит от расположения этой части на отрезке и пропорциональна его длине. Тогда вероятность того, что брошенная точка попадет на отрезок l, являющийся частью отрезка L, вычисляется по формуле: p = l/L где l– длина отрезкаl, а L– длина отрезка L.Можно дать аналогичную постановку задачи для точки, брошенной на плоскую область S и вероятности того, что она попадет на часть этой области s: p = s/S где s – площадь части области, аS– площадь всей области. В трехмерном случае вероятность того, что точка, случайным образом расположенная в теле V, попадет в его частьv, задается формулой:p = v/V где v– объем части тела, аV– объем всего тела. 6 Вычисления вероятностей суммы и произведения. Несовместность и независимость событий. Условная вероятность.  7 Формулы полной вероятности и Байеса.  8 Схема Бернулли. Повторение испытаний. Формула Бернулли   9 Схема Бернулли. Формулы Муавра-Лапласа   10 Схема Бернулли. Формула Пуассона. Поток событий.(см. Рассмотрим серию из п испытаний, в каждом из которых событие А появляется с одной и той же вероятностью р, причем результат каждого испытания не зависит от результатов остальных. Подобная постановка задачи называется схемой повторения испытаний. Найдем вероятность того, что в такой серии событие А произойдет ровно к раз (неважно, в какой последовательности). Интересующее нас событие представляет собой сумму равно-вероятных несовместных событий, заключающихся в том, что А произошло в некоторых к испытаниях и не произошло в остальных п – к испытаниях. Число таких событий равно числу сочетаний из п по к, то есть  , а вероятность каждого из них: pkqn-k, где q = 1 – p– вероятность того, что в данном опыте А не произошло. Применяя теорему сложения для несовместных событий, получим формулу Бернулли: . Таким образом, формула Пуассона  позволяет найти вероятность к появлений события А для массовых (п велико) и редких (р мало) событий. 11 Понятие случайной величины. Общие сведения и основные характеристики. Закон распределения случайной величины  11 Продолжение   12 Функция распределения и ее свойства  13 Дискретные случайные величины. Основные характеристики и способы ее задания  14 Непрерывные случайные величины. Основные характеристики и способы ее задания. Плотность распределения. и ее свойства   15 Числовые характеристики. Математическое ожидание, дисперсия, Среднее квадратическое отклонение    16 Основные дискретные распределения: биноминальное, пуассоновское, геометрическое, гипергеометрическое     17 Основные непрерывные распределения: нормальное, показательное, равномерное.    18 Нормальное распределение (Гаусса). Правило «трех сигм»      19 Неравенства Маркова и Чебышева. Закон больших чисел (теорема Чебышева) и его следствия.   20 Центральная предельная теорема. Ляпунова   21 Основные задачи математической статистики. Основные статические распределения: нормальное, х2, Стыодента        22 Выборка. Вариационный ряд и его характеристики      23 Точечные оценки параметров распределения. Методы моментов и максимального правдоподобия    24 Интервальные оценки параметров распределения.   25 Понятие корреляционной зависимости и регрессии. Выборочное уравнение линейной регрессии   26 Нахождении коэффициентов линейной зависимости методом наименьших квадратов    27Понятие статической гипотезы. Основная и конкурирующая гипотезы (критерий согласия Пирсона и Колмогорова)      |