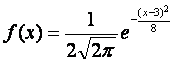вышка. Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю
 Скачать 0.61 Mb. Скачать 0.61 Mb.
|
N (0,5, 2), X и Y независимы. S = X+2Y имеет распределение N (1, 7)
N(0.5, 2), Х и Y независимы. S=X+2Y имеет распределениеВероятность достоверного события равна единице. Вероятность невозможного события равна нулю. Вероятность любого события удовлетворяет неравенству 0 Р(А) 1 Определение 1. События называют несовместными, если в одном и том же испытании появление одного из них исключает появление других. Например, выпадение «орла» при подбрасывании монеты исключает появление в этом же испытании «решки», и наоборот. Определение 2. Несколько событий образуют полную группу, если в результате испытания появление хотя бы одного из них является достоверным событием. Например, при произведении выстрела по мишени (испытание) обязательно будет либо попадание, либо промах; эти два события образуют полную группу. Назовем каждый из возможных результатов испытания элементарным событием, или исходом. Определение 3. Отношение числа благоприятствующих событию А элементарных исходов m к общему числу равновозможных несовместных элементарных исходов n , образующих полную группу, называется вероятностью события А. Вероятность события А обозначается Р(А). Р(А) m/n 1. В урне находятся 10 шаров, 7 из которых белых. Найти вероятность того, что из 6 взятых наугад шаров будет 4 белых. (Ответ: 0,5) 2. В ящике имеется 15 деталей, из которых 10 стандартных. Сборщик наугад берет 3 детали. Найти вероятность того, что все взятые детали будут стандартными.(Ответ: 91 24 ) 3. В лотерее разыгрывается 200 вещевых и 50 денежных выигрышей на каждые 10 тыс. билетов. Чему равна вероятность выигрыша вообще? (Ответ: 0,025) 4. В читальном зале имеется 6 учебников, из которых три нового выпуска. Читатель последовательно, один за другим, взял 2 учебника. Найти вероятность того, что обе взятых книги нового выпуска. (Ответ: 0,2) 5. Три автомашины направлены на перевозку груза. Вероятность исправного состояния первой из них составляет 0,7, второй — 0,8 и третьей — 0,5. Найти вероятность того, что все три автомашины находятся в эксплуатации. (Ответ: 0,28) 4. Сколькими способами можно рассадить 6 человек относительно друг друга за круглым столом? Отв. Р5 = 5! = 120, один сел где угодно. 5. Сколькими способами можно расставить на полке 5 различных книг, чтобы определенные 2 книги стояли: а) рядом? б) не рядом? Отв. а) Есть 4 позиции для пары книг в одном порядке относительно друг друга и 4 – в другом, а для остальных книг 3! способов размещения. Всего 4∙2∙3! = 48.б) Число всех возможных перестановок равно Р5 = 5! = 120, значит искомое число 120 – 48 = 72. 6. Сколько различных перестановок можно образовать из букв следующих слов: а) кобра, б) ворон, в) колобок? Отв. а) все буквы разные, значит 5! = 120; б) для трех разных букв А5 3 = 5∙4∙3 = 60, а две буквы О становятся на оставшиеся места; в) буквы Л и Б ставим А7 2 = 7∙6 = 42 способами, три буквы О С5 3 = 10 способами, значит всего 42∙10 =420. 7. Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4 при условии, что в каждом числе нет одинаковых цифр? Отв. А4 2 = 4∙3 =12. 8. В восьмом классе изучается 16 предметов. Сколькими способами можно составить расписание в субботу, если в этот день должно быть 6 уроков? Отв. А16 6 =16∙15∙14∙13∙12∙11. 9. Сколькими способами 3 награды могут быть распределены между 10 участниками соревнования? Отв. А10 3 = 720. 10. Сколькими способами можно составить расписание занятий на среду, если в этот день должно быть 5 уроков: по алгебре, геометрии, истории, географии и литературе, причем алгебра и геометрия не должны следовать непосредственно друг за другом? Отв. Если алгебра стоит 1-м или 5-м уроком, то для геометрии возможны 3 варианта, а для остальных предметов 3! вариантов. Если алгебра стоит 2-м, 3-м или 4-м уроком, то для геометрии возможны 2 варианта, а для остальных предметов 3! вариантов. Всего 2*3*3! + 3∙2∙3! = 72. 11. На конференции должны выступить докладчики А,В,С и Д, причем В не может выступать раньше А. Сколькими способами можно установить очередность выступлений? Отв. А4 2 = 4∙3 = 12 способов расположить 2 элемента на 4-х позициях в определенном порядке. 12. На семь сотрудников выделены три путевки. Сколькими способами их можно распределить, если: а) все путевки различны, б) все путевки одинаковы? Отв. а) поскольку путевки разные, то рассматриваются упорядоченные подмножества А7 3 = 7∙ 6∙ 5 = 210. б) все путевки одинаковые, значит порядок выдачи не важен: С7 3= 35. 13. Сколькими способами 12 одинаковых монет можно разложить по 5 различным кошелькам так, чтобы ни один кошелек не остался пустым? Отв. Задача о размещении 7 монет в 5 кошельков. С7+5-1 7 = С11 7 = 330. 14. Во взводе 3 сержанта и 30 солдат. Сколькими способами можно выделить одного сержанта и трех солдат для патрулирования? Отв. С3 1 ∙С30 3 = 4060∙3 = 12180. 15. В чемпионате страны по хоккею ( высшая лига ) участвуют 12 команд, причем каждые 2 команды встречаются между собой 4 раза. Сколько матчей играется в течение сезона? Отв. В каждом круге С12 2 = 66, значит всего 284 матча. 16. Сколько экзаменационных комиссий, состоящих из 6 членов, можно образовать из 12 преподавателей? Отв. С12 6 = 924. 17. Сколькими способами можно распределить 15 видов товаров по трем магазинам, если в один магазин надо доставить 8, в другой – 4, а в третий – 3 вида товаров? Отв. С15 8 ∙С7 4 ∙С3 3 . 18. Сколькими способами можно распределить 17 выпускников по трем районам, если в одном из них имеется 9, в другом- 6 и в третьем- 2 вакантных места? Отв. С17 9 ∙С8 6 ∙С2 2 . 19. Сколькими способами можно распределить 6 различных подарков между четырьмя детьми? Отв. 4 6 = 4096. 20. Сколькими способами можно составить набор из 6 пирожных, если имеется 4 сорта пирожных? Отв. С6+4-1 6 = С9 6 = 84. 21. Сколько различных двузначных чисел можно образовать из цифр 1,2,3,4? Отв. 4 2 = 16. 22.Сколько пятизначных чисел можно составить, используя цифры: а) 3, 4, 6, 9; б) 0, 2, 8? Отв. а) 4 5=1024, б) 3 5 -3 4=162 23. Для освещения зала может быть включена каждая из имеющихся 8 ламп. Сколько существует различных способов освещения зала? Отв. 2 8 . Дано выборочное распределение  0 Значение полигона, построенного по данному выборочному распределению, в точке 1280 и моды равны 0 Значение полигона, построенного по данному выборочному распределению, в точке 1280 и моды равны50; 1280 DX = 1.5. Используя свойства дисперсии, найдите D(2X+5). 6 MX = 1.5. Используя свойства математического ожидания, найдите M(2X+5). 8 MX = 5, MY = 2. Используя свойства математического ожидания, найдите M(2X - 3Y). 4 x– стандартная нормальная случайная величина. Случайная величинаx2 имеет распределение χ21 X и Y – независимы. DX = 5, DY = 2. Используя свойства дисперсии, найдите D(2X+3Y). 38 Бросается 5 монет. Какова вероятность того, что три раза выпадет герб? 5/16 Бросается 6 монет. Вероятность того, что герб выпадет более четырех раз равна: Бросаются 2 кубика. Вероятность, что сумма выпавших очков равна 3, составит 1/18 Бросаются 2 монеты. Вероятность того, что выпадут и герб, и решка, равна 0.5 Было проведено выборочное обследование доходов жителей. Оказалось, что половина жителей имеет доходы от 0 до 400 рублей, а половина – от 400 до 2000 рублей. По этим данным построили гистограмму. Она имеет вид 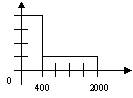 Быстро вращающийся диск разделен на четное число равных секторов, попеременно окрашенных в белый и черный цвет. По диску произведен выстрел. Найти вероятность того, что пуля попадет в один из белых секторов. Предполагается, что вероятность попадания пули в плоскую фигуру пропорциональна площади этой фигуры. 0.5 В группе 25 студентов, из которых отлично учится 5 человек, хорошо – 12, удовлетворительно – 6 и слабо – 2. Преподаватель вызывает студента. Какова вероятность того, что вызванный студент или отличник или хорошист? 17/25 В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8, 9, 11, 12. Выборочная средняя результатов измерений, выборочная и исправленная дисперсии ошибок прибора равны соответственно 10; 2,5; 3,(3) В круг радиусом 10 помещен меньший круг радиусом 5. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в малый круг. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения. 0.25 В круг радиусом 20 см помещен меньший круг радиусом 10 см так, что их центры совпадают. Найти вероятность того, что точка, наудачу брошенная в большой круг, попадет также и в кольцо, образованное построенными окружностями. Предполагается, что вероятность попадания точки в круг пропорциональна площади круга и не зависит от его расположения. 0.75 В пирамиде 5 винтовок, 3 из которых снабжены оптическим прицелом. Вероятность попадания для стрелка при выстреле извинтовкис оптическим прицелом равна 0.95, из обычной винтовки – 0.7. Стрелок наудачу берет винтовку и стреляет. Найти вероятность того, что мишень будет поражена. 0.85 В среднем каждое сотое изделие, производимое предприятием, дефектное. Если взять два изделия, какова вероятность, что оба окажутся исправными? 0.9801 В таблице статистического распределения, построенного по выборке, на одно число попала клякса х = 0,2 В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво х = 5 В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво х = 2 В ящике в 5 раз больше красных шаров, чем черных. Найти вероятность p того, что вынутый наугад шар окажется красным. 5/6 Вариационный ряд выборки: -7, 2, 4, 0, 3, 2, 1, -5 имеет вид –7, -5, 0, 1, 2, 2, 3, 4 Величинаxимеет распределение N(a,s). Вероятность p{|x-a|<2s} равна 0,95 Величинаxимеет распределение N(a,s). Вероятность p{x 0,95 Величинаxимеет распределение N(a,s). Вероятность p{x 0,975 Вероятность выиграть в кости равна 1/6. Игрок делает 120 ставок. Каким асимптотическим приближением можно воспользоваться, чтобы сосчитать вероятность того, что число выигрышей не будет меньше 15? интегральной формулой Муавра-Лапласа Вероятность выиграть в рулетку равна 1/38. Игрок делает 190 ставок. С помощью какой таблицы можно найти вероятность того, что он выиграет не менее 5 раз? распределения Пуассона Вероятность выиграть, играя в рулетку, 1/37. Сделав ставку 100 раз, мы ни разу не выиграли. Заподозрив, что игра ведется не честно, мы решили проверить свою гипотезу, построив 95%-ый доверительный интервал для вероятности выигрыша. По какой формуле строится интервал и что дала проверке в нашем случае? Вероятность любого события всегда удовлетворяет следующему условию она не меньше 0 и не больше 1 Вероятность появлений события А в испытании равна p. Чему равна дисперсия числа появлений события А в одном испытании? p(1-p) Вероятность появления события А в испытании равна 0.1. Чему равно среднеквадратическое отклонение числа появлений события А в одном испытании? 0.3 Вероятность суммы любых случайных событий A и B вычисляется по формуле: р(A+B)=р(A)+р(B)-р(AB) Вероятность того, что дом может сгореть в течение года, равна 0.01. Застраховано 500 домов. Каким асимптотическим приближением можно воспользоваться, чтобы сосчитать вероятность того, что сгорит не более 5 домов? распределением Пуассона Вероятность того, что размеры детали, выпускаемой станком-автоматом, окажутся в пределах заданных допусков, равна 0.96. Каков процент брака q? Какое количество негодных деталей в среднем (назовем это число M) будет содержаться в каждой партии объемом 500 штук? q = 4%; M = 20 Возможные значения случайной величины X таковы: x1 = 2, x2 = 5, x3 = 8. Известны вероятности: р(X = 2) = 0.4; р(X = 5) = 0.15. Найдите р(X = 8). 0.45 Вратарь парирует в среднем 30 % всех одиннадцатиметровых штрафных ударов. Какова вероятность того, что он возьмет ровно два из четырех мячей? 0.2646 Всегда ли верна формула M(X+Y)=M(X)+M(Y) да, всегда Выпущено 100 лотерейных билетов, причем установлены призы, из которых 8 по 1 руб., 2 – по 5 руб. и 1 – 10 руб. Найдите вероятности p0 (билет не выиграл), p1 (билет выиграл 1 руб.), p5 (билет выиграл 5 руб.) и p10 (билет выиграл 10 руб.) событий. p0=0.89; p1=0.08; p5=0.02; p10=0.01 Данвариационныйряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 11, 12, 15. Выборочная медиана для этого ряда – d равна 4,5 Дан вариационный ряд выборки объема n = 7: -5, -3, 0, 1, 1, 4, 16. Выборочная медиана d и выборочное среднеедля этого ряда равны d = 1; = 2 Дан вариационный ряд выборки объема n = 8: -2, 0, 3, 4, 6, 9, 12, 16. Выборочная медиана d и выборочное среднеедля этого ряда равны d = 5; = 6 Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12. Выборочная медиана для этого ряда – d равна 4 Дана выборка объема n = 10. Статистическое распределение этой выборки имеет вид  Тогда выборочное среднеедля этой выборки равно Тогда выборочное среднеедля этой выборки равно=3,4 Дана выборка объема n = 10: 2, 3, 5, 5, 6, 6, 7, 8, 9. Выборочное среднее равно Дана выборка объема n = 5: -2, -1, 1, 3, 4. Выборочное среднееи выборочная дисперсия S2 равны Дана выборка объема n = 5: 2, 3, 5, 7, 8. Выборочное среднееи выборочная дисперсия S2 равны Дана выборка объема n = 5: -3, -2, 0, 2, 3. Выборочное среднееи выборочная дисперсия S2 равны Дана выборка объема n = 5: -4, -2, 2, 6, 8. Выборочное среднееи выборочная дисперсия S2 равны = 2, S2 = 20,8 Дана выборка объема n = 5: -6, -4, 0, 4, 6. Выборочное среднееи выборочная дисперсия S2 равны = 0, S2 = 20,8 Дана выборка объема n = 7: 3, 5, -2, 1, 0, 4, 3. Вариационный ряд для этой выборки и размах вариационного ряда –2, 0, 1, 3, 3, 4, 5; размах равен 7 Дана выборка объема n: х1, х2, …, хn. Выборочная средняя равна. Тогда статистический центральный момент k-го порядка находится по формуле Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить на 5 единиц, то выборочное среднее увеличится на 5, а выборочная дисперсия S2 не изменится Дана выборка объема n: х1, х2, …, хn. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее возрастет в 5 раз, а выборочная дисперсия S2 увеличится в 25 раз Дана выборка объема n: х1, х2, …, хn. Статистический (или эмпирический) начальный момент k-го порядка находится по формуле ak = Дана выборка объема n: х1, х2, х3, …, хn. Выборочное среднее находится по формуле Дана выборка объема n: х1, х2, х3, …, хn. Ее выборочное среднее равно. Выборочная дисперсия находится по формуле Дана выборка: 0, 5, 2, 8, 2, 6, 1, 5. Вариационный ряд для этой выборки и его размах 0, 1, 2, 2, 5, 5, 6, 8; размах выборки 8 Дана конкретная выборка объема n = 10: 2, 2, 5, 5, 4, 3, 4, 2, 2, 5. Статистическое распределение этой выборки имеет вид 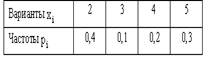 Данные о прибыли, полученной в течение месяца, за последние 5 месяцев оказались следующими  С помощью метода наименьших квадратов по этим точкам строится прямая регрессии. Эта прямая для прибыли в марте дает значение (Указание. Определить это значение без построения прямой регрессии) С помощью метода наименьших квадратов по этим точкам строится прямая регрессии. Эта прямая для прибыли в марте дает значение (Указание. Определить это значение без построения прямой регрессии)1056 Дано статистическое распределение выборки 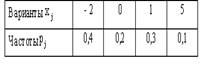 Выборочное среднееи выборочная дисперсия S2 равны Выборочное среднееи выборочная дисперсия S2 равны= 0, S2 = 4,4 Дано статистическое распределение выборки 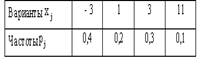 Выборочное среднееи выборочная дисперсия S2 равны Выборочное среднееи выборочная дисперсия S2 равны= 1, S2 = 17,6 Дано статистическое распределение выборки 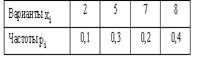 График эмпирической функции распределения для этой выборки имеет вид График эмпирической функции распределения для этой выборки имеет вид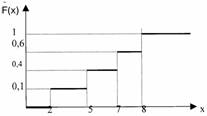 Дано статистическое распределение выборки объема n=50 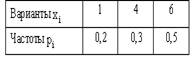 Эмпирическая функция распределения для этого ряда имеет вид Эмпирическая функция распределения для этого ряда имеет вид Дано статистическое распределение выборки с числом вариант m: 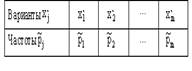 Выборочное среднее находится по формуле Выборочное среднее находится по формулеДано статистическое распределение выборки с числом вариант m: 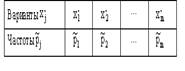 Выборочная средняя равна. Тогда статистический центральный момент k-го порядка находится по формуле: Выборочная средняя равна. Тогда статистический центральный момент k-го порядка находится по формуле:Дано статистическое распределение выборки с числом вариант m: 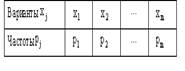 Выборочная средняя равна. Тогда выборочная дисперсия S2 находится по формуле Выборочная средняя равна. Тогда выборочная дисперсия S2 находится по формулеДано статистическое распределение выборки с числом вариант m:  Статистический (или эмпирический) начальный момент k-го порядка находится по формуле Статистический (или эмпирический) начальный момент k-го порядка находится по формулеДано статистическое распределение выборки: 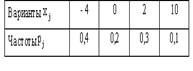 Выборочное среднееи выборочная дисперсия S2 равны Выборочное среднееи выборочная дисперсия S2 равны= 0, S2 = 17,6 Дано статистическое распределение выборки: 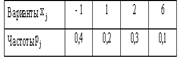 Выборочное среднееи выборочная дисперсия S2 равны Выборочное среднееи выборочная дисперсия S2 равны= 1, S2 = 4,4 Два стрелка стреляют по мишени. Вероятность попадания в цель у одного стрелка 0.7, у другого – 0.8. Найти вероятность того, что цель будет поражена. 0.94 Два стрелка стреляют по разу в общую цель. Вероятность попадания в цель у одного стрелка 0.6, у другого – 0.7. Найти вероятность того, что цель будет поражена двумя пулями. 0.42 Два стрелка стреляют по разу в общую цель. Вероятность попадания в цель у одного стрелка 0.8, у другого – 0.9. Найти вероятность того, что цель не будет поражена ни одной пулей. 0.02 Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема nх=42 и ny=20 с такими характеристиками: проходит Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема nх=42 и ny=20 с такими характеристиками: (-2, 2) Для вероятности р по выборке объема n с помощью величеныи таблиц нормального распределения строится доверительный интервал. Если увеличить объем выборки в 100 раз, длина доверительного интервала примерно уменьшится в 10 раз Для выборки объема n=9 рассчитали выборочную дисперсию S2=3,86. Исправленная дисперсия равна 4,34 Для контроля качества продукции завода из каждой партии готовых изделий выбирают для проверки 1000 деталей. Проверку не выдерживают в среднем 80 изделий. Равной чему можно принять вероятность того, что наугад взятое изделие этого завода окажется качественным? Сколько примерно бракованных изделий (назовем это число M) будет в партии из 10000 единиц? p = 0.92; M = 800 Для обработки наблюдений методом наименьших квадратов построена прямая. Ее график: 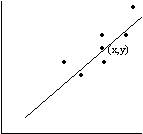 Для построения доверительного интервала для дисперсии надо пользоваться таблицами распределения Пирсона ( Для построения доверительного интервала для оценки вероятности надо пользоваться таблицами нормального распределения Для проверки гипотезы о равенстве 2-х генеральных средних надо пользоваться таблицами распределения Стьюдента Для проверки на всхожесть было посеяно 2000 семян, из которых 1700 проросло. Равной чему можно принять вероятность p прорастания отдельного семени в этой партии? Сколько семян в среднем (назовем это число M) взойдет из каждой тысячи посеянных? p=0.85; M=850 Для сравнения 2-х генеральных средних совокупностей X и Y из них извлекли выборки объема n и m соответственно. Для проверки гипотезы о том, чтоmх=my, надо вычислить статистику 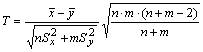 Для того чтобы построить доверительный интервал математического ожидания по выборке, когда дисперсия неизвестна, необходимо определить выборочное среднее , выборочное среднеквадратическое s Для того, чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, во сколько раз надо увеличить число наблюдений в 4 раза Для того, чтобы по выборке объема n= 10 построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы распределения Стьюдента. Для того, чтобы построить 95%-ый доверительный интервал для математического ожиданияmслучайной величины, распределенной нормально с известной дисперсиейs2 по выборке объема n, вычисляетсяи используется формула Для упрощения счета из всех значений выборки вычли 1280. При этом эмпирическое среднее уменьшится на 1280 Для упрощения счета из всех значений выборки вычли 1280. При этом эмпирическая дисперсия не изменится Если вероятность р некоторого события неизвестна, а для оценки этой вероятности производится n испытаний, то 95%-ый доверительный интервал для величины р находится по формуле I0,95 (p)= Если вероятность события A есть р(A), то чему равна вероятность события, ему противоположного? 1-р(A) Если имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событие A может наступить после реализации одного из Hi и известны вероятности P(A/Hi), то P(A) вычисляется по формуле Полной вероятности Завод в среднем дает 27% продукции высшего сорта и 70% – первого сорта. Найдите вероятность того, что наудачу взятое изделие не будет высшего или первого сорта. 0.03 Завод в среднем дает 28% продукции высшего сорта и 70% – первого сорта. Найдите вероятность того, что наудачу взятое изделие будет или высшего, или первого сорта. 0.98 Задана таблица распределения случайной величины. Найти C. 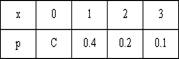 0.3 Задана таблица распределения случайной величины. Найти р(X < 3). 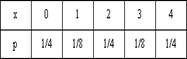 5/8 Значение кумуляты, построенной по таблице, в точке 170, и медианы равны 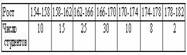 0,8; 166 Из генеральной совокупности извлечена выборка, данные по ней сведены в таблицу 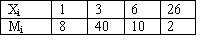 Оценка генеральной средней Оценка генеральной средней4 Из колоды, состоящей из 36 карт, вынимают наугад две карты. Вероятость того, что попадут две карты одинаковой масти равна Из колоды, состоящей из 36 карт, вынимают наугад две карты. Вероятность того, что это будут две пики равна Известно, что X |
N(1, 5)
Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что из двух взятых наугад изделий окажутся неисправными оба?
0.0001
Изделия изготавливаются независимо друг от друга. В среднем одно изделие из ста оказывается бракованным. Чему равна вероятность того, что из 200 взятых наугад изделий 2 окажутся неисправными?
0.271
Имеется группа из n несовместных событий Hi, в сумме составляющих все пространство, и известны вероятности P(Hi), а событие A может наступить после реализации одного из Hi, и заданы вероятности P(A/Hi). Известно, событие A произошло. Вероятность, что при этом была реализована Hi вычисляется по формуле
Байеса
Количество поражений шахматиста в течение года имеет распределение Пуассона с параметром λ=6. Вероятность того, что шахматист в течение года проиграет не более двух партий равна
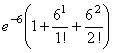
Количество Х принимаемых по телефону за час звонков имеет распределение Пуассона. Среднее количество принимаемых за час звонков λ=5. Вероятность того, что за час будет принято точно 3 звонка равна
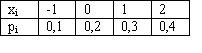
Куплено 1000 лотерейных билетов. На 80 из них упал выигрыш по 1 руб., на 20 – по 5 руб., на 10 – по 10 руб. Какая таблица описывает закон распределения выигрыша?
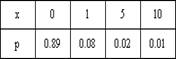
Куплено 500 лотерейных билетов. На 40 из них упал выигрыш по 1 руб., на 10 – по 5 руб., на 5 – по 10 руб. Найдите средний выигрыш, приходящийся на один билет.
0.28
Лампочки изготавливаются независимо друг от друга. В среднем одна лампочка из тысячи оказывается бракованной. Чему равна вероятность того, что из двух взятых наугад лампочек окажутся исправными обе?
0.998001
Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения
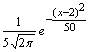 , равны
, равны2; 25
Математическое ожидание и дисперсия случайной величины, распределенной равномерно на отрезке [1,3], равны
2; 1/3
Медиана выборки
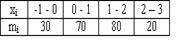 равна
равна1
Монету бросали 100 раз. 70 раз выпал орел, для проверки гипотезы о симметричности монеты строим доверительный интервал и проверяем, попали ли мы в него. По какой формуле строится доверительный интервал, и что даст проверка в нашем конкретном случае?
I 0,95 (p) =
На некоторой фабрике машина А производит 40% продукции, а машина B – 60%. В среднем 9 из 1000 единиц продукции, произведенных машиной А, и 1 из 250, произведенных машиной B, оказываются бракованными. Какова вероятность, что случайно выбранная единица продукции окажется бракованной?
0.006
На некотором заводе было замечено, что при определенных условиях в среднем 1.6% изготовленных изделий оказываются неудовлетворяющими стандарту и идут в брак. Равной чему можно принять вероятность того, что наугад взятое изделие этого завода окажется качественным? Сколько примерно непригодных изделий (назовем это число M) будет в партии из 1000 изделий?
p = 0.984; M = 16
На отрезке длиной 20 см помещен меньший отрезок L длиной 10 см. Найти вероятность того, что точка, наудачу поставленная на большой отрезок, попадет также и на меньший отрезок. Предполагается, что вероятность попадания точки на отрезок пропорциональна длине отрезка и не зависит от его расположения.
0.5
Наблюдения проводились над системой (х, у) 2-х величин. Результаты наблюдения записаны в таблицу
 Коэффициент корреляции равен
Коэффициент корреляции равенr = 1
Наблюдения проводились над системой (х, у) 2-х величин. Результаты наблюдения записаны в таблицу
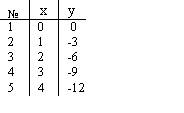 Коэффициент корреляции равен
Коэффициент корреляции равенr = -1
Наблюдения проводятся над системой (X : Y) двух случайных величин. Выборка состоит из пар чисел: (х1: y1), (х2: y2), …, (хn : yn). Найдены, Sдля хi и, Sдля yi (
Плотность распределения f(x) можно найти по функции распределения F(х) по формуле
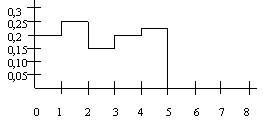
По выборке 1, 0, 4, 3, 1, 2, 3, 2, 0, 4 построен полигон

По выборке объема 100 надо построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого известна. Для этого необходимо воспользоваться
таблицами нормального распределения
По выборке объема n из нормального распределения с известной дисперсиейs2 строится доверительный интервал для математического ожидания. Если объем выборки увеличить в 25 раз, длина доверительного интервала
уменьшится в 5 раз
По выборке объема n из нормального распределения с неизвестной дисперсией строится доверительный интервал для математического ожидания. Объем выборки увеличиваем в 16 раз. В предположении, что величиныи S2 при этом изменятся мало, длина доверительного интервала примерно
уменьшится в 4 раза
По выборке объема n=100 вычислены выборочное среднее – 54 и выборочная дисперсия – 16. 95%-ый доверительный интервал для генерального среднего равен
(53,2; 54,8)
По выборке объема n=9 вычислили выборочное среднее 15 и исправленную несмещенную дисперсию 9. 95%-ый доверительный интервал для математического ожиданияm(t8,0.95=2,3) равен
(12,7; 17,3)
По выборке построен доверительный интервал для генерального среднего. Оказалась, что генеральное среднее по такому объему выборки определяется с точностью 0,2. Чтобы повысить точность вдвое, надо объем выборки
увеличить в 4 раза
По выборке построена гистограмма
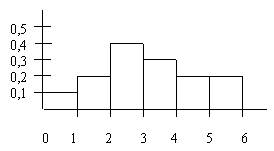 Медиана равна
Медиана равна3
По выборке построена гистограмма
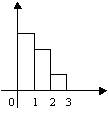 Медиана равна
Медиана равна1
По выборке построена гистограмма
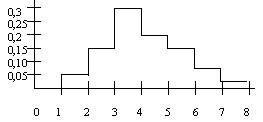 По виду гистограммы можно предполагать, что генеральная совокупность, из которой произведена выборка, имеет распределение
По виду гистограммы можно предполагать, что генеральная совокупность, из которой произведена выборка, имеет распределениенормальное
По выборке построена гистограмма
 По виду гистограммы можно предполагать, что генеральная совокупность, из которой произведена выборка, имеет распределение
По виду гистограммы можно предполагать, что генеральная совокупность, из которой произведена выборка, имеет распределениеравномерное
По выборке построена статистическая таблица распределения
d = 2,5
По выборке построена таблица статистического распределения выборки. Эта таблица
По выборке построена таблица статистического распределения выборки, имеющая вид.
Построить гистограмму и полигон распределения роста школьников по таблице
 Построить графически моду, найти медиану
Построить графически моду, найти медиану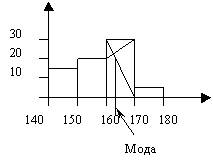 Медиана равна 160
Медиана равна 160При изготовлении детали заготовка должна пройти четыре операции. Полагая появление брака на отдельных операциях событиями независимыми, найти (с точностью до 4-х знаков после запятой) вероятность изготовления нестандартной детали, если вероятность брака на первой стадии операции равна 0.02, на второй – 0.01, на третьей – 0.02, на четвертой – 0.03.
0.0777
Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0.03, второго – 0.06. Найти вероятность того, что при включении прибора откажет только второй элемент.
0.0582
Прибор состоит из двух элементов, работающих независимо. Вероятность выхода из строя первого элемента при включении прибора – 0.05, второго – 0.08. Найти вероятность того, что при включении прибора оба элемента будут работать.
0.874
Проверяется гипотеза о том, что вероятность выиграть в рулетку 1/37. Доверительный интервал с уровнем доверия 95% строится по формуле
n =900
Производится n независимых испытаний, в которых вероятность наступления события A равна p. Вероятность того, что событие A наступит m раз
вычисляется по формуле Бернулли
Производится n независимых испытаний, в которых вероятность наступления события A равна p. n велико. Вероятность того, что событие A наступит m раз, вычисляется по формуле или используются асимптотические приближения?
используются асимптотические приближения
Производится выборка объема n=100 из генеральной совокупности, имеющей распределение N (20,4). По выборке строится выборочное среднее. Эта случайная величина имеет распределение
N (20;0,4)
Рабочий обслуживает три станка. Вероятность того, что в течение часа станок потребует внимания рабочего, равна для первого станка 0.1, для второго – 0.2 и для третьего – 0.15. Найти вероятность того, что в течение некоторого часа хотя бы один из станков потребует внимания рабочего.
0.388
Распределение выборки рабочих по времени, затраченному на обработку одной детали, приведено в таблице
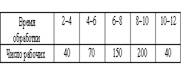 Эмпирическое среднее времени, затрачиваемого на обработку одной детали,
Эмпирическое среднее времени, затрачиваемого на обработку одной детали,7,52
Рулетка размечается с помощью меток – 00, 0, 1, ...36. Метки при игре не имеют преимуществ друг перед другом. Игрок делает 114 попыток. Какова вероятность ни разу не выиграть?
0.05
С первого станка на сборку поступает 40% деталей, остальные 60% со второго. Вероятность изготовления бракованной детали для первого и второго станка соответственно равна 0.01 и 0.04. Найдите вероятность того, что наудачу поступившая на сборку деталь окажется бракованной.
0.028
Самое маленькое значение в выборке 0, самое большое 8, медиана 2. По этой выборке построена гистограмма
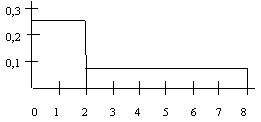
Случайная величина X принимает значения 7, -2, 1, -5, 3 с равными вероятностями. Найдите MX.
0.8
Случайная величина X распределена «нормально с параметрами 0,1» - (N[0,1]). Для нее вероятность попасть внутрь интервала [-3,3] равна
0,9973
Случайная величина X распределена «нормально с параметрами 3,2» - (N[3,2]). Случайная величина Y=(X-3)/2. Ее математическое ожидание, дисперсия и тип распределения
MY = 0; DY = 1, распределение нормальное
Случайная величина X распределена «нормально с параметрами 3,2» - (N[3,2]). Для нее вероятность попасть внутрь интервала [-1,7] равна
0,9544
Случайная величинаxраспределена равномерно на [0,1],hраспределена равномерно на [2,6]. Ее можно получить изxс помощью линейного преобразования
h=4x+2
Случайная величина X распределена равномерно на отрезке [0, 1]. Случайная величина Y=X+2 будет иметь
равномерное распределение на отрезке [2,3]
Случайная величина распределена «нормально с параметрами 3,2» (N[3,2]). Ее математическое ожидание и дисперсия равна
MX = 3; DX = 4
Случайная величина распределена равномерно на отрезке [0, 2]. Ее математическое ожидание равно
1
Случайная величина распределена равномерно на отрезке [0, 4]. Вероятность попасть в интервал [1,3] равна
0,5
Случайная величина распределена равномерно на отрезке [0, 5]. P1 - вероятность, что случайно брошенная точка попадет на отрезок [0,1]. P2 - вероятность, что случайно брошенная точка попадет на отрезок [3,4]. Тогда можно утверждать, что
P1 = P2
События A и B называются несовместными, если:
р(AB)=0
События называются независимыми, если:
р(AB)=р(A)р(B)
Состоятельной, но смещенной точечной оценкой параметра является
эмпирическая дисперсия S2
Станок-автомат производит изделия трех сортов. Первого сорта – 80%, второго – 15%. Чему равна вероятность того, что наудачу взятое изделие будет или второго, или третьего сорта?
0.2
Страхуется 1600 автомобилей; вероятность того, что автомобиль может попасть в аварию, равна 0.2. Каким асимптотическим приближением можно воспользоваться, чтобы сосчитать вероятность того, что число аварий не превысит 350?
интегральной формулой Муавра-Лапласа
Стрелок попадает в цель в среднем в 8 случаях из 10. Какова вероятность, что, сделав три выстрела, он два раза попадет?
0.384
Студенту предлагают 6 вопросов и на каждый вопрос 4 ответа, из которых один верный, и просят дать верные ответы. Студент не подготовился и выбирает ответы на - угад. Какова вероятность того, что он правильно ответит ровно на половину вопросов? (С точностью до 3-х знаков после запятой)
0.132
Теннисист идет на игру. Если ему дорогу перебежит черная кошка, то вероятность победы 0,2; если не перебежит, то – 0,7. Вероятность, что кошка перебежит дорогу – 0,1; что не перебежит – 0,9. Вероятность победы:
0,1·0,2+0,9·0,7
Условной вероятностью события B при условии, что событие A с ненулевой вероятностью произошло, называется:
р(B/A)=р(AB)/р(A)
ФормулаD(-X)=D(X)
верна
Функцию распределения F(х) можно найти по плотности вероятности f(х) по формуле
Человеку, достигшему 20-летнего возраста, вероятность умереть в течение 20 лет равна 0.02. Какова вероятность того, что из 200 застраховавшихся на 20 лет человек в возрасте 20 лет ни один не умрет?
0.0183
Человеку, достигшему 20-летнего возраста, вероятность умереть на 21-м году жизни равна 0.01. Какова вероятность того, что из 200 застраховавшихся человек в возрасте 20-ти лет один умрет через год?
0.271
Человеку, достигшему 60-летнего возраста, вероятность умереть на 61-м году жизни равна 0.09. Какова вероятность того, что из трех человек в возрасте 60 лет ни один не будет жив через год?
0.000729
Человеку, достигшему 60-летнего возраста, вероятность умереть на 61-м году жизни равна 0.09. Какова вероятность того, что из трех человек в возрасте 60 лет хотя бы один умрет через год? (с точностью до 4-х знаков после запятой).
0.2464
Чему равна вероятность достоверного события?
1
Чему равна вероятность невозможного события?
0
Число грузовых машин, проезжающих мимо бензоколонки, относится к числу легковых машин, как 3:2. Известно, что в среднем одна из 30 грузовых и одна из 25 легковых машин останавливается для заправки. Найти вероятность того, что проезжающая машина будет заправляться.
0.036
Эмпирический коэффициент корреляции между весом и ростом для выборки
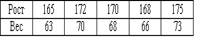 равен
равен1
Математическое ожидание и дисперсия случайной величины, распределенной равномерно на отрезке [1; 3], равны 2; 1/3
Случайная величина распределена «нормально с параметрами 3 и 2»(N[3,2]). Ее математическое ожидание и дисперсия равны MX = 3; DX = 4
Случайная величина распределена равномерно на отрезке [0, 4]. Вероятность попасть в интервал [1, 3] равна 0,5
Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения , равны 2; 5
Известно, что X

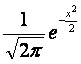 , равны 0; 1
, равны 0; 1