вышка. Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю

• Название: Вероятность достоверного события равна единице. Вероятность невозможного события равна нулю
• Анкор: вышка
• Дата: 25.06.2022
• Размер: 0.61 Mb.
• Имя файла: vyshka.docx
• Тип: Документы; #615127
• страница: 5 из 6

423. При проверке гипотезы о числовом значении математического ожидания нормального распределения при известной дисперсии критерий вычисляется по формуле

424. При проверке гипотезы о числовом значении дисперсии нормального распределения критерий вычисляется по формуле

425. При проверке гипотезы о равенстве дисперсий  двух нормальных распределений критерий вычисляется по формуле

426. Для того чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, число наблюдений надо увеличить в 4 раза

427. По выборке объема n  = 100 вычислены выборочное среднее 54 и выборочная дисперсия 16.  95 %-ый доверительный интервал для генерального среднего равен (53,2;54,8)

• 
  Для того чтобы построить 95%-ый доверительный интервал для математического ожидания μ случайной величины, распределенной нормально с известной дисперсией σ²  по выборке объема n , вычисляется   и используется формула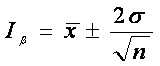
  
• 
  При выборке объема n = 9 вычислили выборочное среднее 15 и исправленную несмещенную дисперсию 9. 95 %-ый доверительный интервал для математического ожидания μ (t_{8; 0,95} = 2,3) равен (12,7; 17,3)
  
• 
  Для того чтобы вдвое увеличить доверительный интервал, построенный для математического ожидания, число наблюдений надо уменьшить в 4 раза
  
• 
  Для построения доверительного интервала для дисперсии надо пользоваться таблицами распределения Пирсона (χ_n²)
  
• 
  Для того чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы распределения Стьюдента
  
• 
  Для того чтобы по выборке объема n построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого известна, нужны таблицы нормального распределения
  
• 
  По выборке объема n из нормального распределения с неизвестной дисперсией строится доверительны интервал для математического ожидания. Объем выборки увеличиваем в 16 раз. В предположении, что величины   и S ²   при этом изменяются мало, длина доверительного интервала уменьшается в 4 раза
  
• 
  По выборке объема n из нормального распределения с известной дисперсией σ ²  строится доверительный интервал для математического ожидания. Если объем выборки увеличить в 25 раз, длина доверительного интервала уменьшается в 5 раз
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,17, объем выборки  =36 и среднее квадратичное отклонение  =6 будет равен ( ) (72,60; 77,74)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,16, объем выборки  =49 и среднее квадратичное отклонение  =7 будет равен ( ) (72,59; 77,73)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,15, объем выборки  =64 и среднее квадратичное отклонение  =8 будет равен ( ) (72,58; 77,72)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,14, объем выборки  =81 и выборочное среднее квадратичное отклонение s=9 будет равен ( ) (74,133; 76,147)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,13, объем выборки  =100 и выборочное среднее квадратичное отклонение s=10 будет равен ( ) (73,46; 76,79)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,12, объем выборки  =121 и среднее квадратичное отклонение  =11 будет равен ( ) (73,16; 77,08)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,11, объем выборки  =144 и среднее квадратичное отклонение  =12 будет равен ( ) (73,21; 77,01)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,1, объем выборки  =169 и среднее квадратичное отклонение  =13 будет равен ( ) (72,53; 77,67)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,08, объем выборки  =225 и среднее квадратичное отклонение  =15 будет равен ( ) (73,12; 77,04)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,07, объем выборки  =256 и среднее квадратичное отклонение  =16 будет равен ( ) (73,07; 77,07)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,06, объем выборки  =289 и среднее квадратичное отклонение  =17 будет равен ( ) (73,10; 77,02) Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,05, объем выборки  =324 и среднее квадратичное отклонение  =18 будет равен ( ) (73,09; 77,01)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,04, объем выборки  =361 и среднее квадратичное отклонение  =19 будет равен ( ) (73,08; 77,00)
  
• 
  Доверительный интервал, для оценки математического ожидания  нормального распределения с надежностью 0,95, зная выборочную среднюю  =75,03, объем выборки  =400 и среднее квадратичное отклонение  =20 будет равен ( ) (73,07; 76,99)
  
• 
  Для выборки объема n = 9 рассчитали выборочную дисперсию S² = 3,86. Исправленная дисперсия равна 4,20
  
• 
  Дана выборка объема n  = 5: -4, -2, 2 6, 8. Выборочное среднее  и выборочная дисперсия S ²  равны  = 2, S ²  = 20,8 
  
• 
  Выборочное среднее   и выборочная дисперсия S ²  равны= 1, S ²  = 17,6  
  
• 
  Дана выборка объема n: х₁, х₂ , …, х_n . Статистический (или эмпирический) начальный момент k-го порядка находится по формуле a_{k  =}    
  
• 
  Выборочная средняя равна  . Тогда выборочная дисперсия S ² находится по формуле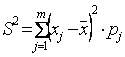
  
• 
  Дана выборка объема n  = 5: -3, -2, 0, 2, 3. Выборочное среднее  и выборочная дисперсия S ²  равны  = 0, S ²  = 5,2 
  
• 
  Выборочное среднее   и выборочная дисперсия S ²  равны  = 2, S ²  = 17,6  
  
• 
  Коэффициент корреляции равен r = -1    
  
• 
  Наблюдения проводились над системой (X : Y) двух случайных величин. Выборка состоит из пар чисел: (х₁ : у₁), (х₂ : у₂), …, (х_n: у_n). Найдены  , S _x² для х _i  и  , S _у² для у _i  (S _x =   S _у =  ). Причем тогда выборочный коэффициент корреляции r _xy находится по формуле   
  
• 
  В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8, 9, 11, 12. Выборочная средняя результатов измерений, выборочная и исправленная дисперсии ошибок прибора равны соответственно 10; 2,5; 3,(3) 
  
• 
  Дана выборка объема n: х₁, х₂ , …, х_n . Ее выборочное среднее равно  . Выборочная дисперсия находится по формуле   S²  ₌         
  
• 
  Дана выборка объема n= 5: 2, 3, 5, 7, 8. Выборочное среднее   и выборочная дисперсия S ²  равны    = 5, S ²  = 5,2     
  
• 
  Случайная величина распределена «нормально с параметрами 3,2»(N[3,2]). Ее математическое ожидание и дисперсия равна MX = 3; DX = 4
  
• 
  Выборочное среднее   и выборочная дисперсия S ²  равны  = 0, S ²  = 4,4  
  
• 
  Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения , равны 2; 5  
  
• 
  Известно, что X

N (0, 3), YN (0.5, 2), X и Y независимы. S = X+2Y имеет распределение N (1, 7)  

Выборочное среднее находится по формуле   

Дана выборка объема n= 5: -6, -4, 0, 4, 6. Выборочное среднее   и выборочная дисперсия S ²  равны  = 0, S ²  = 5,2    

Производится выборка объема n=100 из генеральной совокупности, имеющей распределение N (20, 4). По выборке строится выборочное среднее  . Эта случайная величина имеет распределение N (20; 0,4)   

Из генеральной совокупности извлечена выборка, данные по ней сведены в таблицу 4    

Случайная величина Х распределена «нормально с параметрами 3,2» - (N[3,2]). Случайная величина Y = (X-3)/2. Ее математическое ожидание, дисперсия и тип распределения MY = 0; DY= 1, распределение нормальное     

Коэффициент корреляции равен 1

Распределение выборки рабочих по времени, затраченному на обработку одной детали, приведено в таблице 7,52

Дано статистическое распределение выборки с числом вариант m:

Дифференциальные уравнения связывают производные функции различных порядков. независимую переменную, искомую функцию и ее производную. искомую функцию и ее производную

Дифференциальное уравнение 1-го порядка символически записывается в виде

С помощью подстановки  , решают дифференциальные уравнения второго порядка

Частным решением дифференциального уравнения 2-го порядка является функция

Стандартную форму записи   имеет уравнение линейное

Уравнением вида   является с разделяющимися переменными

Решением дифференциального уравнения является Функция

Порядком дифференциального уравнения называется наивысший порядок производной функции

С помощью подстановки   решается дифференциальное уравнение линейное

В дифференциальных уравнениях высших порядков вводится замена переменной для понижения порядка дифференциального уравнения

 Дифференциальное уравнение вида   является уравнением однородное

Уравнение первой степени относительно y и   является линейное

Дифференциальное уравнение вида   является уравнением с разделяющимися переменными

Дифференциальное уравнение вида   является уравнением линейное

Дифференциальное уравнение первого порядка решается с помощью однократного интегрирования

С помощью подстановки    решается уравнение однородное

Дифференциальное уравнение вида   является уравнением с разделяющимися переменными

Общим решением дифференциального уравнения 1-ого порядка является функция

Если при умножении каждого аргумента функции на произвольный множитель λ вся функция умножается на  , т.е.  , то это дифференциальное уравнение однородное

С помощью подстановки   решается уравнение линейное

Обыкновенным дифференциальным уравнением II-го порядка называется уравнение вида

Общее решение уравнения  , где  - заданные числа, когда корни характеристического уравнения комплексные представимо в виде

Неоднородное линейное дифференциальное уравнение II-го порядка с постоянными коэффициентами имеет вид

Частное решение   неоднородного линейного дифференциального уравнения II-го порядка с постоянными коэффициентами со специальной правой частью конструируется в виде  , где   -кратность корня соответствующего характеристического уравнения, равного параметру 

Общее решение уравнения  , где  - заданные числа, когда корни характеристического уравнения действительные равные, представимо в виде

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид   

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид  

Общее решение дифференциального уравнения   имеет вид  

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид   

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид  

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Общее решение дифференциального уравнения   имеет вид

Объектом и языком исследования в экономико-математическом моделировании является