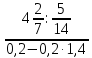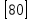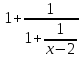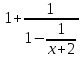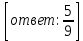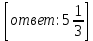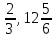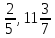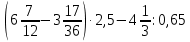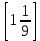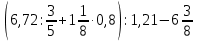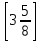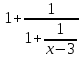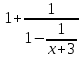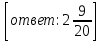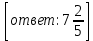1 папка Степени. Тема 1 Развитие понятия о числе 2
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
ОглавлениеТема №1 Развитие понятия о числе 2 Тема№2 Корни, степени и логарифмы 12 Тема №1 Развитие понятия о числе1.1 Действительные числаИррациональным числом называется бесконечная непериодическая десятичная дробь. Действительным числом называется бесконечная десятичная дробь, т. е. дробь вида +а0, а2, а3 … или – а0, а2, а3 …, где а0 — целое неотрицательное число, а каждая из букв а1, а2, а3, ... — это одна из десяти цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Пусть x1, х2, …, хn — последовательные приближения действительного числа х с точностью до 1, до 0,1, до 0,01 и т. д. Тогда погрешность приближения | х - хп| при  стремится к 0. стремится к 0.Все правила действий над рациональными числами сохраняются и для действительных чисел. Правило перевода обыкновенной дроби в десятичную Для обращения обыкновенной дроби в десятичную дробь выполняется деление числителя дроби на знаменатель Пример: 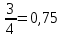 3 4 0 0,75 30 2 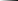 8 820 20 0 Правило перевода конечной десятичной дроби в обыкновенную дробь Чтобы обратить десятичную дробь в обыкновенную дробь, достаточно в числителе дроби записать число, стоящее после запятой, а в знаменателе единице с нулями, причем нулей должно быть столько, сколько цифр справа запятой. 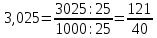 Правило перевода бесконечной периодической дроби в обыкновенную В основе такого перевода лежит тот факт, что периодическую часть периодической десятичной дроби можно рассматривать как сумму членов бесконечно убывающей геометрической прогрессии. Например, 0,(73)=0,73+0,0073+0,000073+…или 4,07(254)=4,07+(0,00254+0,00000254+0,00000000254+…). Бесконечная десятичная дробь, в которой, начиная с некоторого разряда, цифры повторяются, называется периодической. Например, 0,333..., 0,6777...; Любую обыкновенную дробь можно записать в виде конечной десятичной дроби, либо бесконечной периодической дроби. Правило перевода бесконечной периодической дроби в обыкновенную: Чтобы обратить периодическую дробь в обыкновенную, надо из числа стоящего до второго периода, вычесть число, стоящее до первого периода, и записать эту разность числителем, а в знаменателе написать цифру 9 столько раз, сколько цифр в периоде, и после десяток дописать столько нулей, сколько цифр между запятой и первым периодом. Например, а) Числитель искомой дроби равен периоду данной дроби, т.е. 45, а знаменатель содержит цифру 9 столько раз, сколько цифр в периоде, т.е. два раза. 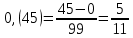 б) Числитель искомой дроби равен периоду данной дроби, т.е. 3, а знаменатель содержит цифру 9 столько раз, сколько цифр в периоде, т.е. один раз. 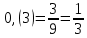 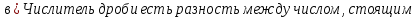 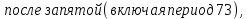 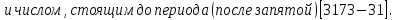 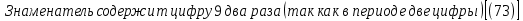 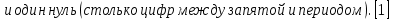 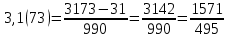 г) Числитель дроби есть разность между числом, стоящим после запятой (включая период 1), и числом, стоящим до периода (после запятой). Знаменатель содержит цифру 9 один раз (так как после одна цифра) и один нуль (столько цифр между запятой и периодом). 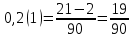 1.2 Приближенные вычисления, погрешностиПриближенное значение величины записывается следующим образом Определение. Разность Определение. Модуль разности между точным числом Определение. Число Определение. Относительной погрешностью Утверждение. Абсолютная погрешность Число Определение. Границей относительной погрешности 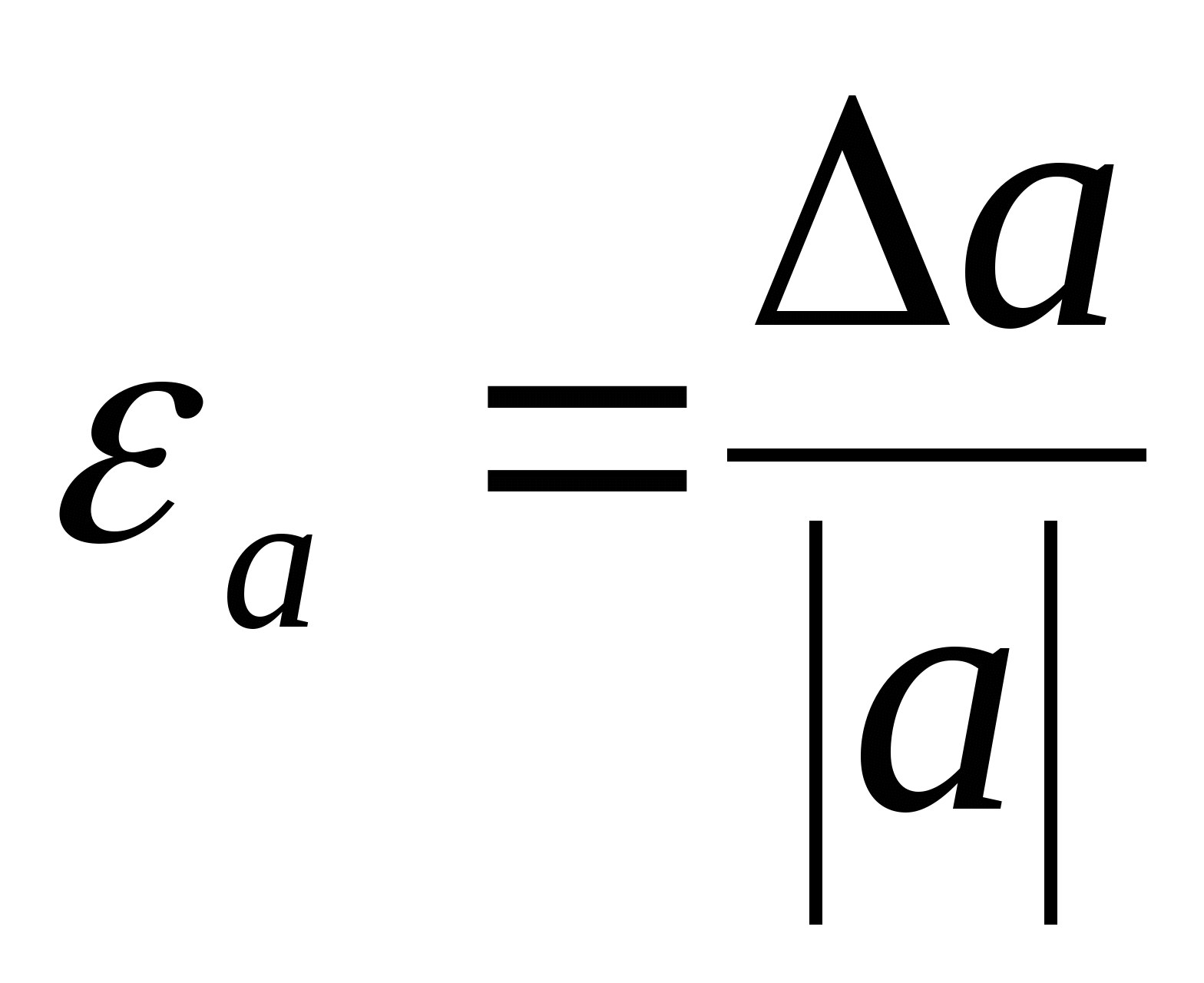 . .Определение. Абсолютная погрешность, допустимая при округлении, называется погрешностью округления. Утверждение. Округление с недостатком до единиц некоторого разряда состоит в отбрасывании единиц всех младших разрядов. Утверждение. Округление с избытком до единиц некоторого разряда состоит в том, что число единиц данного разряда увеличивают на единицу. . 4. Решение ключевых задач. Пример 1. Даны приближенные значения Какое из этих приближения является лучшим? Решение. 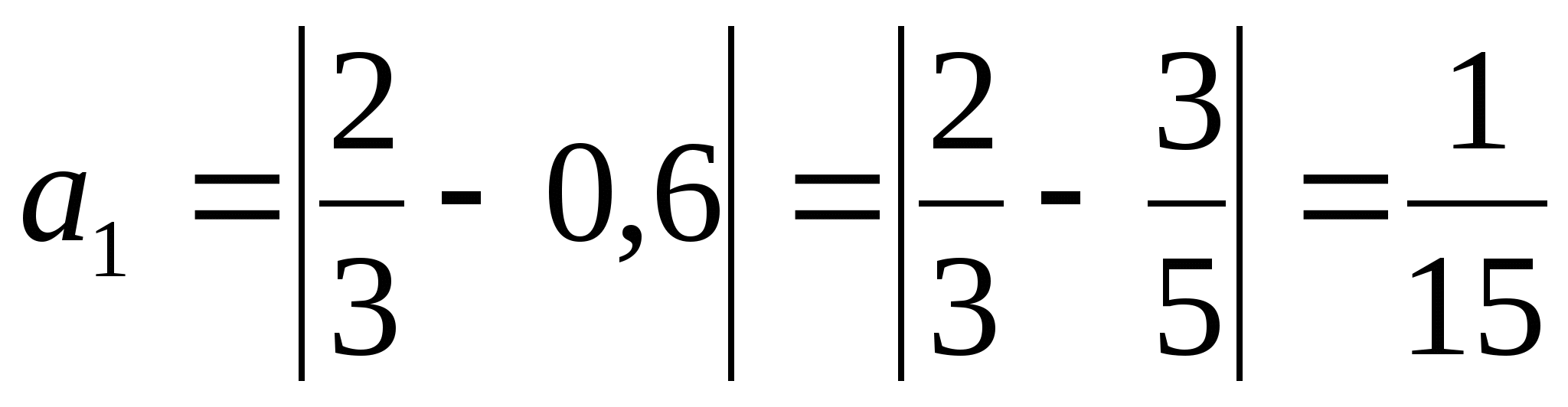 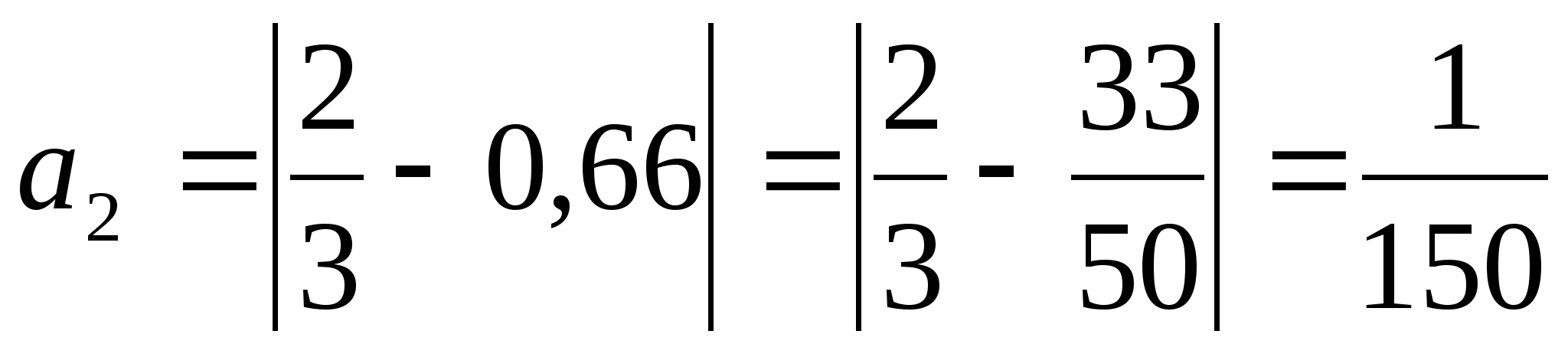 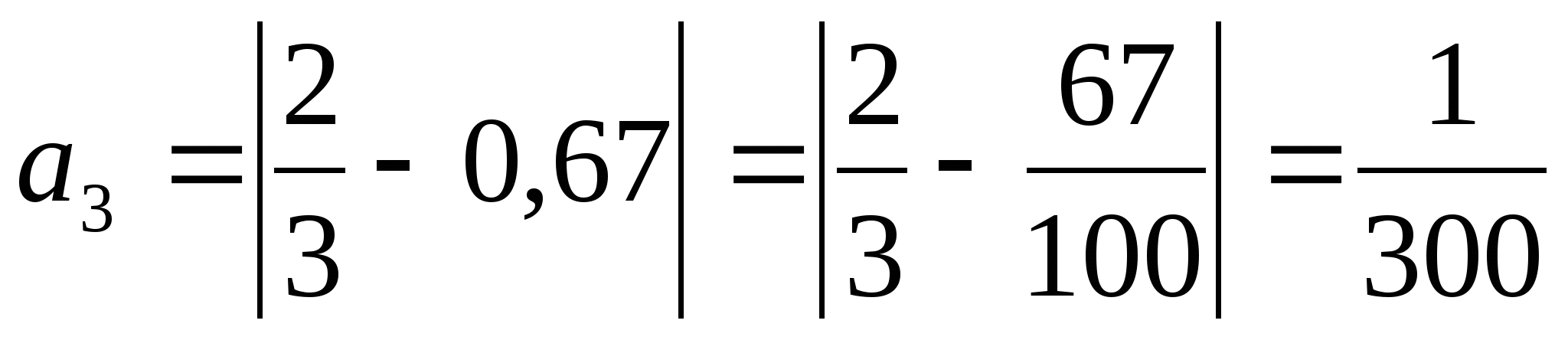 Ответ: лучшим приближение числа Пример 2. Округлить с избытком до сотых, десятых и единиц число Решение. До сотых Ответ: погрешности округления равны: 5. Решение упражнений. Пример 1. В результате измерений получили, что длина ручки равна 16 см, а длина комнаты равна 750 см. Какой можно сделать вывод о качестве измерений, если граница абсолютной погрешности равна Решение. Найдем относительную погрешность этих измерений. Ответ: качество измерения комнаты выше, чем качество измерения ручки. Пример 2. Округлить с недостатком до сотых, десятых и единиц число 44, 376. Решение. До сотых Ответ: погрешности округления равны: Пример 3. Если число 5,756 округлить до десятых с недостатком до 5,7, то Самостоятельная работа №1Задание 1. Вычислите, ответ округлите до 0,001 1) 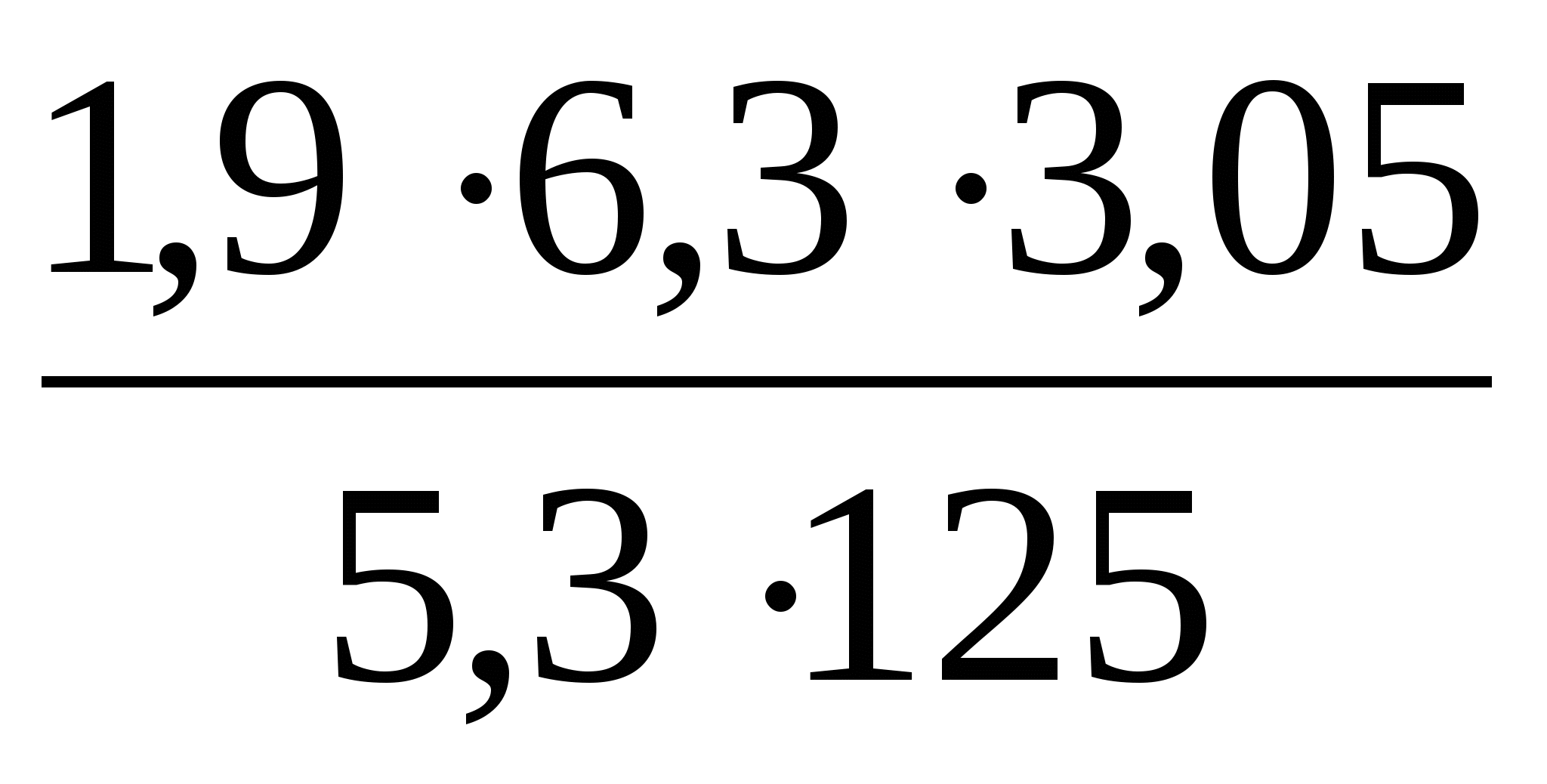 ; 2) ; 2) 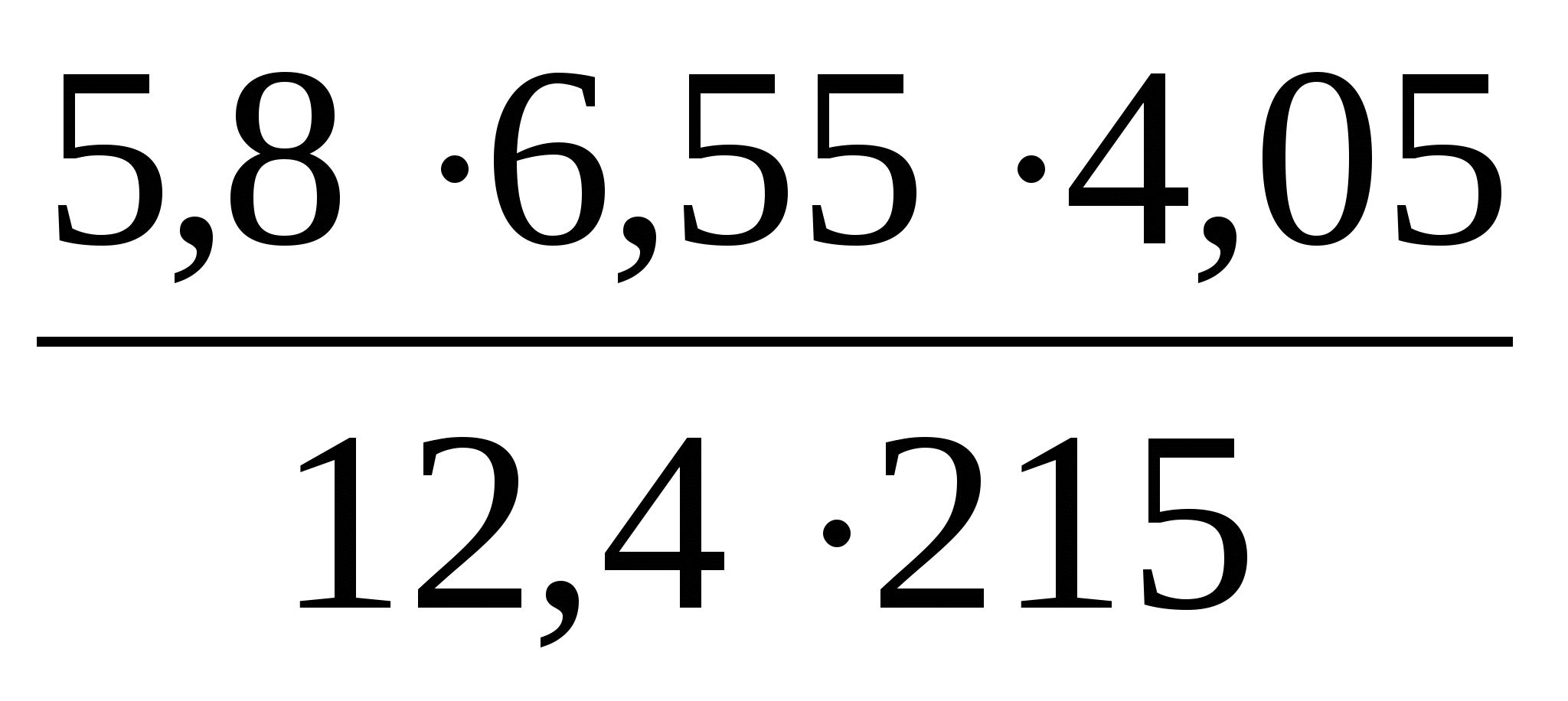 ; ;3) 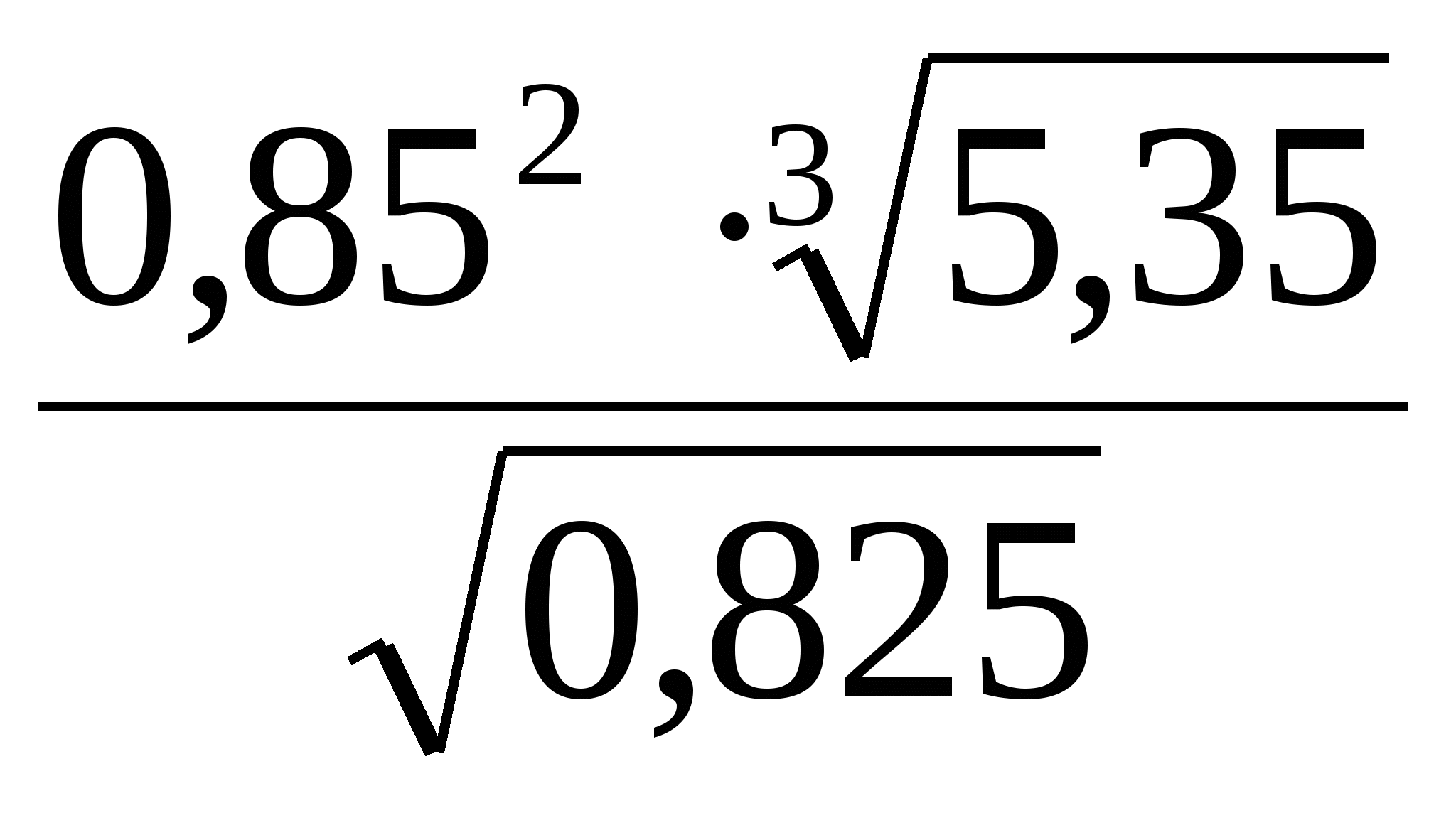 ; 4) ; 4) 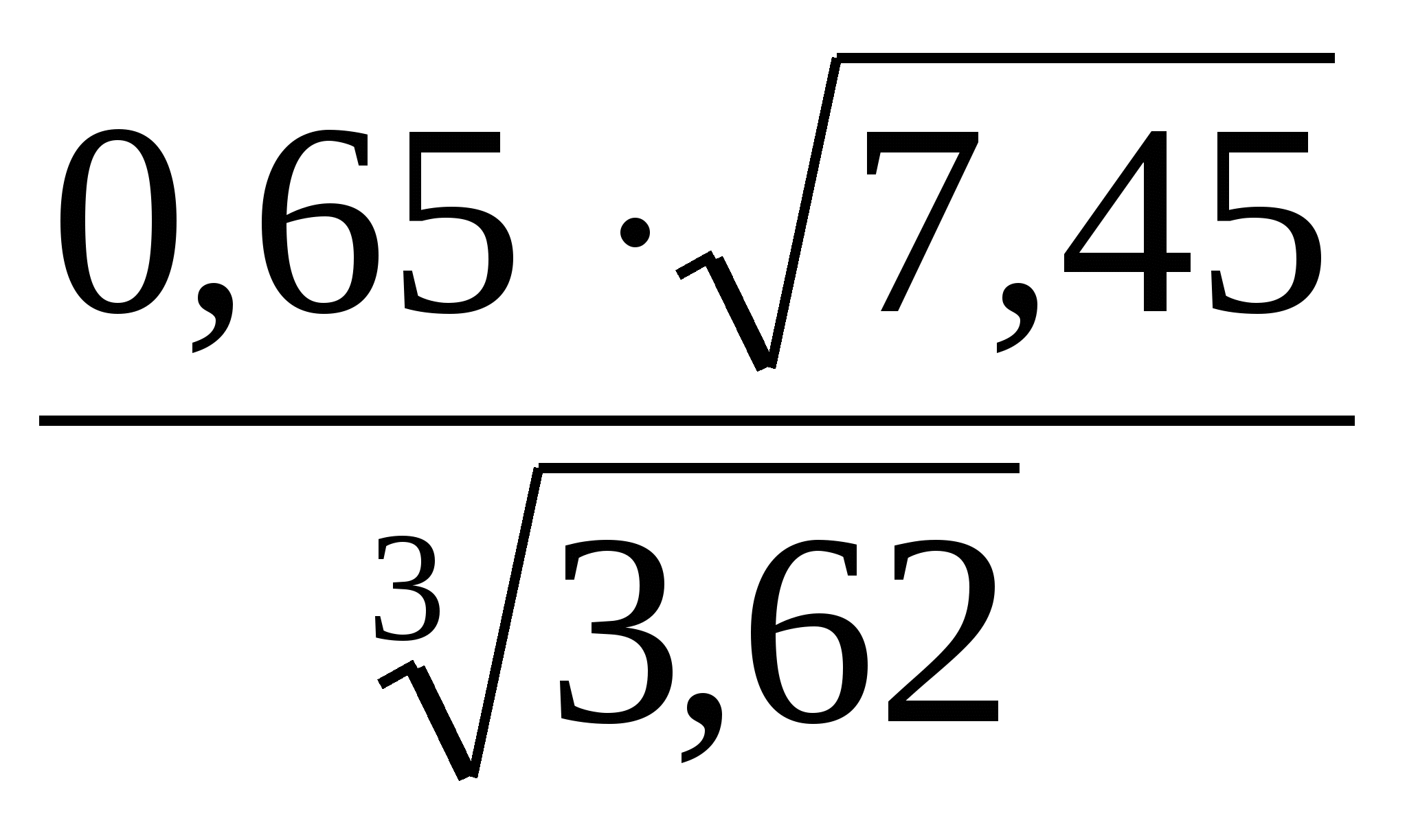 ; ;5) 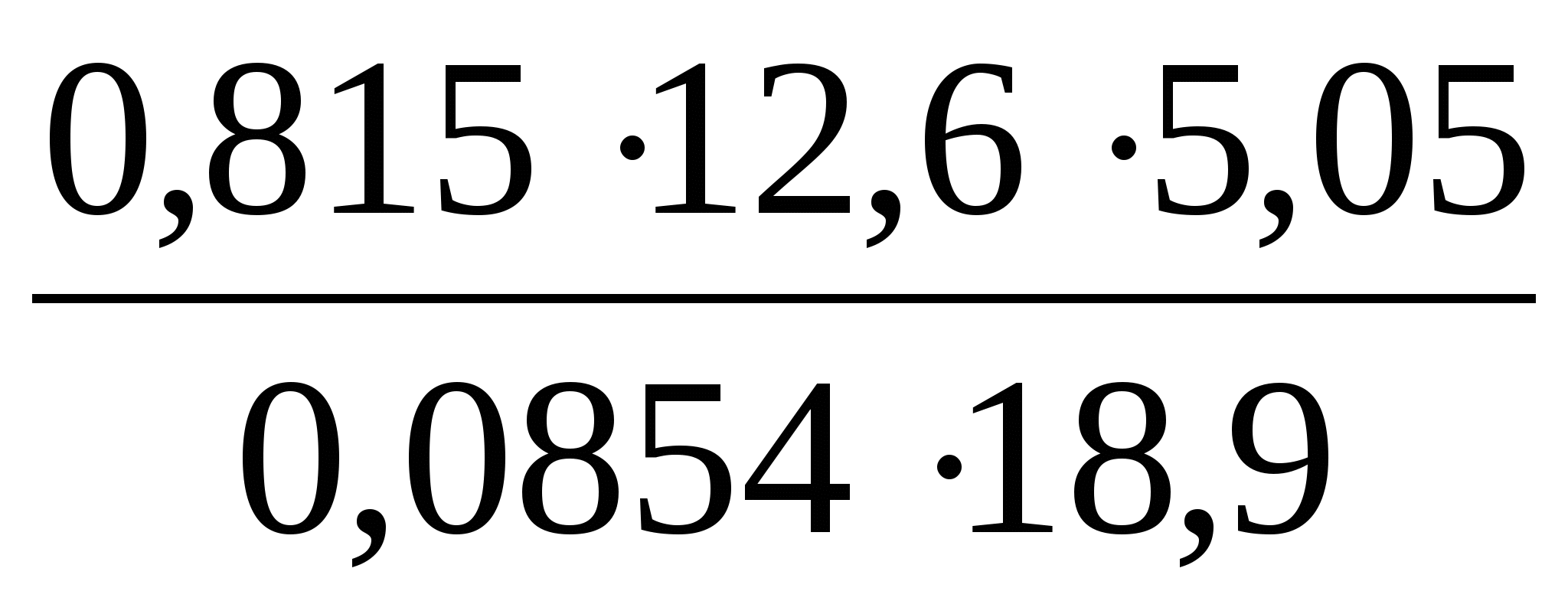 ; 6) ; 6) 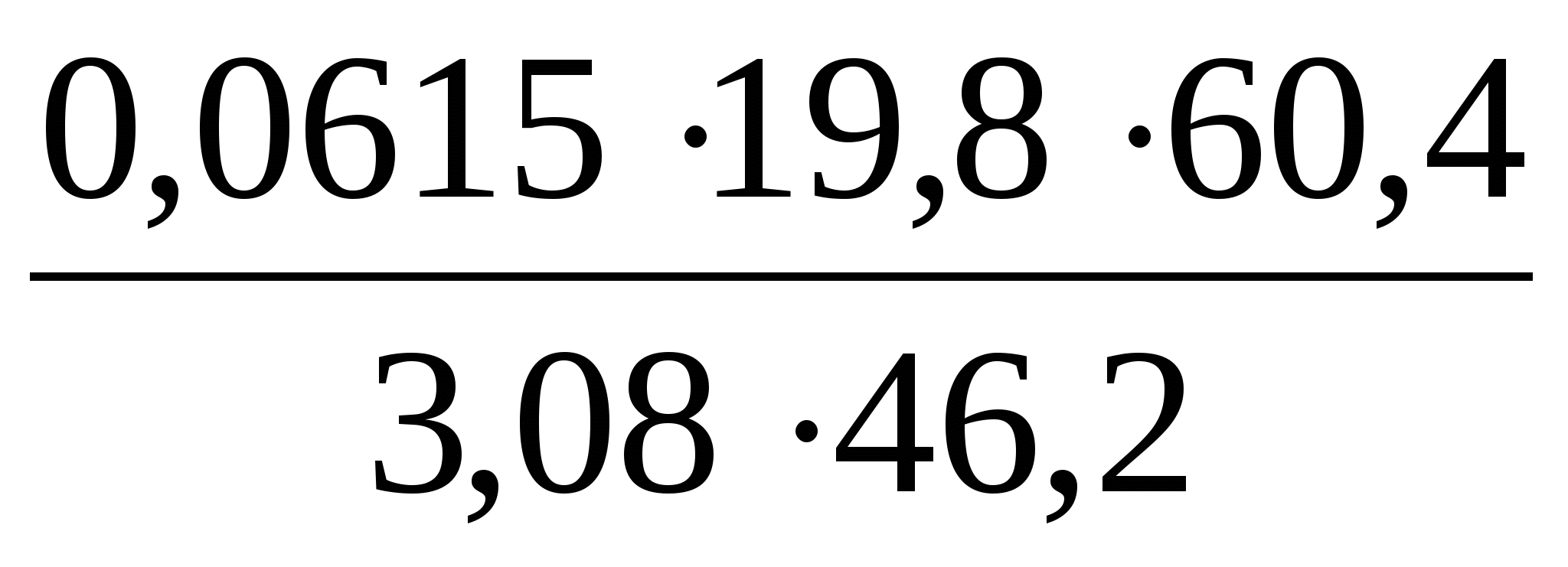 . .Задание 2. 1) Масса ящика с конфетами равна 2) Найти площадь прямоугольника ширины Задание 3. Найдите относительную погрешность числа 1) 2) 3)
1.3 Комплексные числа, их виды. Действия над комплексными числами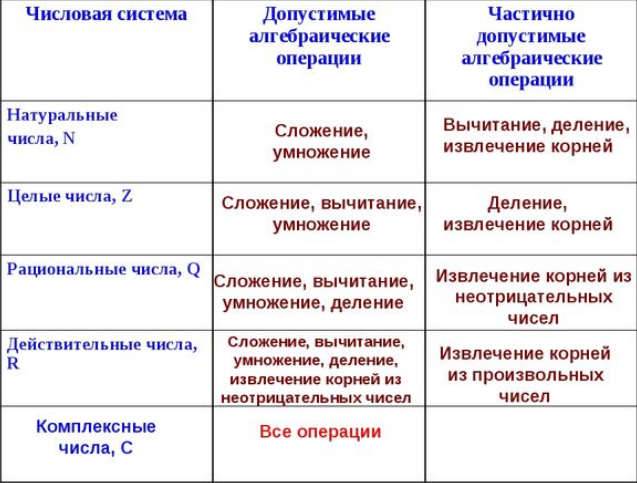    Самостоятельная работа №2Вариант 1. 1. Даны два комплексных числа Z1= (10 + 2i ) и Z2=(1 – 6i ). Найдите их сумму, разность, произведение и частное. 2. Проверьте правильность следующих утверждений: а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Для проверки возьмите числа: Z1=2i, Z2=-3i б) Произведение двух чисто мнимых чисел равно действительному числу. Для проверки возьмите числа: Z1=-5i, Z2=3i в) Квадрат чисто мнимого числа равен действительному отрицательному числу. Для проверки возьмите числа: Z1=10i г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Для проверки возьмите числа: Z1=7i, Z2=3 ***Дополнительное задание: Найдите два комплексных числа, сумма и произведение которых равны 2. Вариант 2. 1.Даны два комплексных числа z1= (12 + 2i ) и z2=(3 – 4i ). Найдите их сумму, разность, произведение и частное. 2. Проверьте правильность следующих утверждений: а) Сумма и разность чисто мнимых чисел есть чисто мнимое число. Для проверки возьмите числа: Z1=2i, Z2=-3i б) Произведение двух чисто мнимых чисел равно действительному числу. Для проверки возьмите числа: Z1=-5i, Z2=3i в) Квадрат чисто мнимого числа равен действительному отрицательному числу. Для проверки возьмите числа: Z1=10i г) Произведение чисто мнимого числа на действительное равно чисто мнимому числу. Для проверки возьмите числа: Z1=7i, Z2=3 ***Дополнительное задание: Найдите два комплексных числа, сумма и произведение которых равны 2. 1.4 Степени мнимой единицы. Решение квадратных уравнений с отрицательным дискриминантом  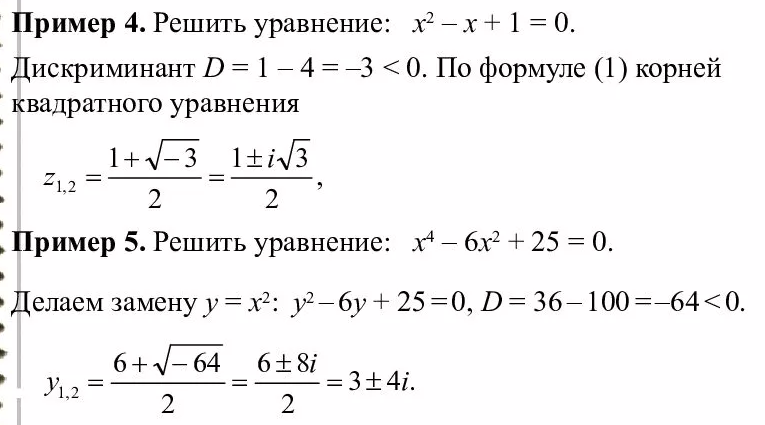 Самостоятельная работа №31. Вычислить: 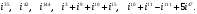 2. Среди приведенных примеров укажите : а) чисто мнимые комплексные числа; б) чисто действительные комплексные числа; в) сопряженные комплексные числа; г) равные комплексные числа: 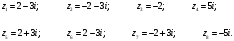 3. Выполнить действия: 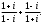 Ответ. Ответ. 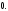 4. На основании равенства комплексных чисел найти действительные числа 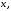 и и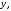 если если 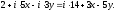 Ответ. Ответ. 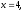 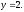 5. Решить квадратные уравнения и проверить выполнение теоремы Виета: а) 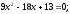 б) б)  Ответ. а) Ответ. а) 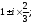 б) б) 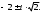 6. Решите уравнения: 1. x2 – 4x + 5 = 0. 2. x2 – x + 10 = 0. 3. x2 – 4x + 13 = 0. 4. x2 – 2x + 15 = 0. 7. Разложите число Z на комплексно сопряженные множители (a и b – действительные числа): Z = 81a²+16b² Z = a²+25b² Z = 9a²+4b² 8. Назовите комплексное число, сопряженное с данным числом: 1+i -2+3i -7-5i - ⅓ + ⅕ i ⅓ + ⅖ i Практическая работа №11,2,3 Выполните действия 4 Представьте в виде обыкновенной дроби 5 Представьте в виде десятичной дроби
|

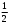 - 2
- 2 ( –3)
( –3)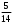 - 2
- 2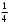 : (0,6 ∙ 3,28 – 5,468) ( 3)
: (0,6 ∙ 3,28 – 5,468) ( 3)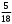 - 5
- 5 +1
+1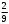 )∙(0,81 :0,4) ( –3,23)
)∙(0,81 :0,4) ( –3,23) - 4
- 4 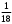 - 1
- 1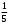 ) ( 5,27)
) ( 5,27)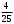 ) ( –3,61)
) ( –3,61) ) ∙ 0,5 – 0,5 ( – 0,649)
) ∙ 0,5 – 0,5 ( – 0,649)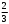 + 2 ∙ ( 0,82 : 0,4 – 2,4 ) = –
+ 2 ∙ ( 0,82 : 0,4 – 2,4 ) = – 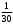
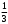 =
= 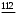
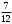 ∙ 0,5) :
∙ 0,5) : 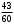
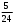 : (
: ( 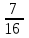 ) = – 10,25
) = – 10,25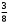 = –0,4142
= –0,4142 +8,5∙(0,021:0,01– 2,51) = –4,235
+8,5∙(0,021:0,01– 2,51) = –4,235