1 папка Степени. Тема 1 Развитие понятия о числе 2
 Скачать 2.5 Mb. Скачать 2.5 Mb.
|
2.3 Вычисление иррациональных выраженийИррациональными выражениями называют выражения, содержащие операцию извлечения корня. Другими словами, иррациональные выражения – это выражения с радикалами (выражения, содержащие в своей записи знаки корня). Преобразование иррациональных выражений производится в соответствии со свойствами арифметических действий с корнями (рациональными степенями). Алгебраические выражения, содержащие операции извлечения корня из переменной или возведения переменной в рациональную степень, не являющуюся целым числом, называются иррациональными относительно этой переменной. Тождественным преобразованием данного выражения называется замена одного выражения другим, тождественно равным ему на некотором множестве. В основе тождественных преобразований рациональных и иррациональных выражений лежат следующие теоретические факты. Свойства степеней с целым показателем: 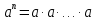 , n- множителей nÎN; а1=а; , n- множителей nÎN; а1=а;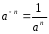 , nÎN, а¹0; а0=1, а¹0; , nÎN, а¹0; а0=1, а¹0;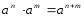 , а¹0; , а¹0;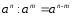 , а¹0; , а¹0;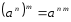 , а¹0; , а¹0;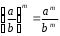 , а¹0, b¹0; , а¹0, b¹0;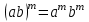 , а¹0, b¹0. , а¹0, b¹0.Формулы сокращенного умножения: 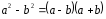 ; ; 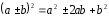 ; ;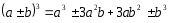 ; ; 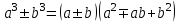 ; ;где а, b, с – любые действительные числа; 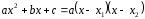 , ,где а¹0, х1 и х2 – корни уравнения 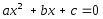 . .Основное свойство дроби и действия над дробями: 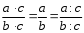 , где b¹0, с¹0; , где b¹0, с¹0;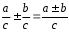 ; ; 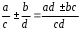 ; ;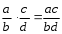 ; ; 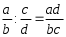 . .Определение арифметического корня и его свойства: 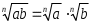 ; ; 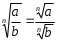 , b¹0; , b¹0; 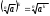 ; ;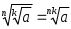 ; ; 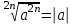 ; ; 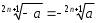 , ,где а, b – неотрицательные числа, nÎN, n³2, mÎN, m³2. Пример: Определить область допустимых значений 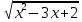 Подкоренное выражение у корня с четным показателем должно быть не отрицательным 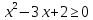 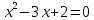 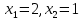 - - + 2 1  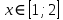 Пример: Приведение подобных слагаемых Пример: Приведение подобных слагаемых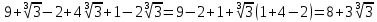 Пример: Использование формул сокращенного умножения 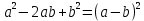 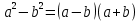 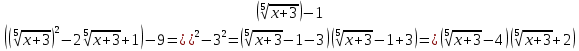 Пример: Преобразование подкоренного выражения с использованием свойств корней. 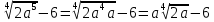 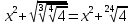 Пример: Вынесите множитель из-под знака корня, если а³0, b³0, с³0: 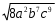 . .Решение: 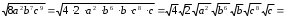 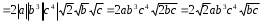 . .Использовали правила действий над корнями и определение модуля числа. Пример: Избавьтесь от иррациональности в знаменателе дроби 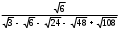 . .Решение: 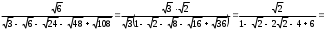 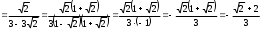 . .Самостоятельная работа № 5
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||