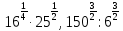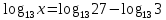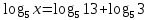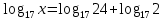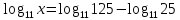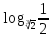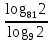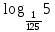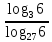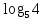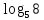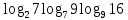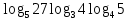1 папка Степени. Тема 1 Развитие понятия о числе 2

• Название: Тема 1 Развитие понятия о числе 2
• Дата: 26.04.2022
• Размер: 2.5 Mb.
• Имя файла: 1 папка Степени.docx
• Тип: Документы; #497216
• страница: 8 из 8

2.4 Свойства логарифмов

Свойства логарифмов

Пусть a>0, a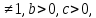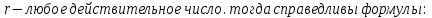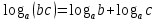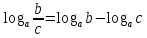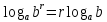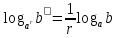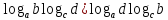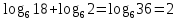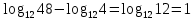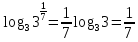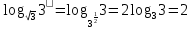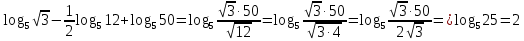

Самостоятельная работа № 7

В-1

1. 
   Вычислите:
   

log₃6 + log₃ 18 - log₃4

log₁₂ 4 + log₁₂ 36

2. Решите уравнение:

log₂3х = log₂ 4 + log₂6

в) 2 log₈х = log₈ 2,5 + log₈10

В-2

1.Вычислите:

1) log₆12 + log₆3

2) log₅250 – log₅2

2. Решите уравнение:

log₆12 + log₆ х = log₆24

log_ах = 2log_а 3 + log_а5

2.5 Основно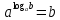е логарифмическое тождество

– основное логарифмическое тождество.
Пример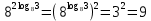

Самостоятельная работа № 8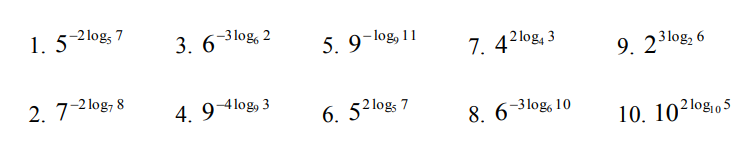

В1

1. 
   Вычислить: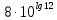
   
2. 
   Упростить, применив основное логарифмическое тождество: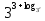
   
3. 
   Вычислить: .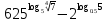
   

В-2

1. 
   Вычислить: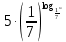
   
2. 
   Упростить, применив основное логарифмическое тождество: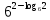
   
3. 
   Вычислить: .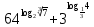
   

Практическая работа №5

1 Найдите ОДЗ

2 Вычислите по основному логарифмическому тождеству

3, 4, 5 Вычислить выражение используя свойства логарифмов

	В-1		В-2
1		1
2		2
3		3
4	, ,	4	, ,
5		5
	В-3		В-4
1		1
2		2
3		3
4	, ,	4	, ,
5		5

2.6 Переход от одного основания логарифма к другому основанию.

Переход от одного основания к другому осуществляется по формулам: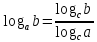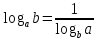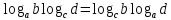







Пример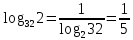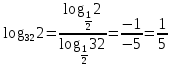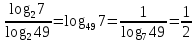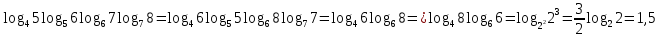

Самостоятельная работа № 9

2.7 Потенцирование и логарифмирование

Потенцирование и логарифмирование

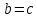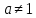Переход от равенства к равенству 1оg_а b = 1оg_а c (а, b, с > 0, ) называют логарифмирова­нием.

Пример

Прологарифмируйте выражение: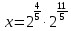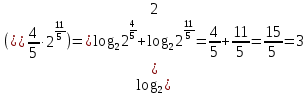

,

Переход от равенства 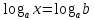к равенству x=b называется потенцированием.

Пример

Пропотенцируйте выражение: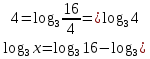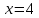

,

Самостоятельная работа № 10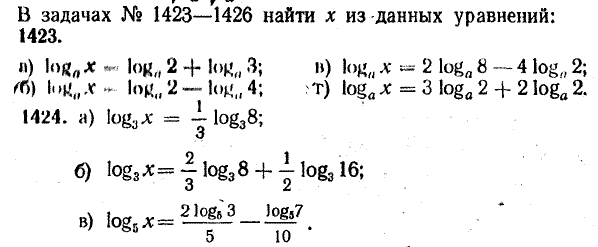

Практическая работа №6

1 Прологарифмируйте выражение

2 Пропотенцируйте выражения:

Вычислить выражение используя свойства логарифмов

4. Выразить данный логарифм с основанием 4

5. Вычислите

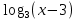
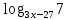
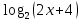
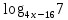
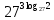
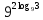
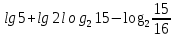
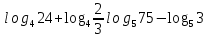
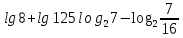
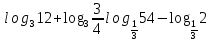
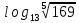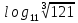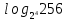
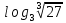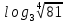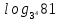
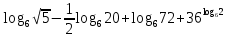
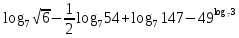
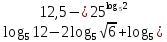
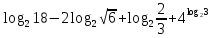
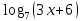
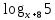
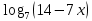
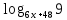
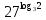
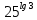
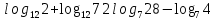
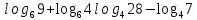
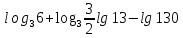
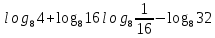
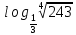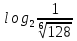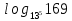
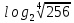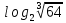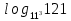
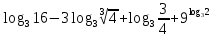
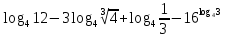
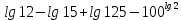
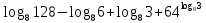
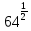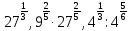
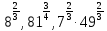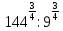
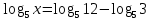
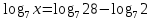
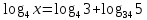
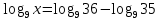
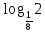
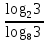
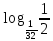
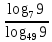
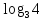
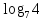
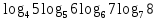
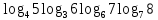
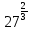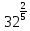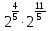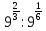
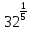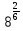	В-1		В-2
1	,	1	,
2		2
3		3
4		4
5		5
	В-3		В-4
1	, , ,	1	, ,
2		2
3		3
4		4
5		5