дискретная математика. Экзаменационные вопросы по ДМ. 1. Понятие высказывания. Основные логические операции

• Название: 1. Понятие высказывания. Основные логические операции
• Анкор: дискретная математика
• Дата: 17.12.2021
• Размер: 153.7 Kb.
• Имя файла: Экзаменационные вопросы по ДМ.docx
• Тип: Документы; #307175

1.Понятие высказывания. Основные логические операции.

Высказывание — форма мышления, в которой что-либо отрицается или утверждается об объектах, признаках или отношениях.

Операции:

• 
  НЕ — инверсия, отрицание
  
• 
  ИЛИ — дизъюнкция, лог. сложение
  
• 
  И — конъюнкция, лог. умножение
  
• 
  ЕСЛИ..,ТО — импликация, следование, лог. сравнение
  
• 
  Т и Т ТОГДА — эквиаленция, лог. Равенство
  

2.Формулы логики. Таблица истинности и методика её построения.

Формулы алгебры логики определяются след образом

1. 
   Любая лог переменная есть формула
   
2. 
   Если А формула, то (А) тоже формула
   
3. 
   Если А,В формулы то 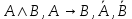и тд тоже формулы
   
4. 
   Других формул нет
   

Таблица истинности—табл, в которой отражены все логические значения, формулы при всех возможных значениях входящих лог переменных

Методика построения

1.Столбцы=кол-во переменных + кол-во действий

2. Строки= шапка табл + 2ⁿ, где n – кол-во переменных

3.Законы логики.
4.Равносильные преобразования.
5.Понятие булевой функции.

Функция f зависит от nпеременных (х₁, х₂, х₃ и тд) называется булевой, если функция f и любой из его аргументов х_i принимает значение из множества ∈ {0,1}

6.Способы задания ДНФ.
7.Способы задания КНФ.
8.Операция двоичного сложения и её свойства.
9.Многочлен Жегалкина.

Полином Жегалкина—представление булевой функции с помощью констант, операции конъюнкции и двоичного сложения.

10.Основные классы функций.
11.Полнота множества. Теорема Поста.
12.Общие понятия теории множеств. Способы задания.
13.Основные операции над множествами и их свойства.

• 
  Пересечение
  
• 
  Объединение
  
• 
  Вычитание
  

14.Мощность множеств. Графическое изображение множеств на

диаграммах Эйлера-Венна. Декартово произведение множеств.

Мощностью множества называется число элементов входящих в него.

Декартовым произведением множеств А и В называется множеством АхВ, состоящее из всех упорядоченных х пар, в которых 1-й элемент принадлежит множеству А, 2-й элемент принадлежит множеству В.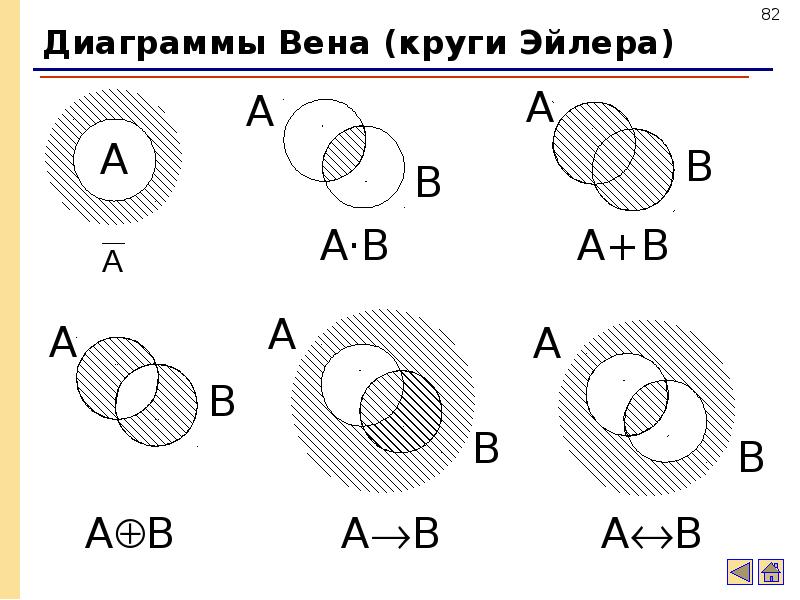



15.Отношения. Бинарные отношения и их свойства.
16.Теория отображений.
17.Алгебра подстановок.
18.Понятие предиката. Логические операции над предикатами.
19.Кванторы существования и общности. Построение отрицаний к предикатам, содержащим кванторные операции.
20.Основные понятия теории графов.
21.Виды графов: ориентированные и неориентированные графы.
22.Способы задания графов. Матрицы смежности и инцидентности для графа.
23.Эйлеровы и гамильтоновы графы.
24.Деревья.
25.Машина Тьюринга.