лингвистическая переменная. Лекция_Лингвистическая переменная_нечеткий_вывод_семантические с. Основы нечеткой логики Лингвистическая переменная
 Скачать 225.96 Kb. Скачать 225.96 Kb.
|
|
Нечеткий вывод Основы нечеткой логики Лингвистическая переменная Лингвистической называется переменная, принимающая значения из множества слов или словосочетаний некоторого естественного или искусственного языка. Множество допустимых значений лингвистической переменной называется терм-множеством. Термом (term) называется любой элемент терм–множества. В теории нечетких множеств терм формализуется нечетким множеством с помощью функции принадлежности. Значениями лингвистической переменной являются нечеткие множества, символами которых являются слова и предложения в естественном или формальном языке, Лингвистической переменной называется набор <β,T,U,G,M>, где β - наименование лингвистической переменной; Т - множество ее значений (терм-множество), представляющих собой наименования нечетких переменных, областью определения каждой из которых является множество X. Множество T называется базовым терм - множеством лингвистической переменной; G - синтаксическая процедура, позволяющая оперировать элементами терм-множества T, в частности, генерировать новые термы (значения). Множество T ∪ G(T), где G(T) - множество сгенерированных термов, называется расширенным терм - множеством лингвистической переменной; М - семантическая процедура, позволяющая превратить каждое новое значение лингвистической переменной, образуемое процедурой G, в нечеткую переменную, т.е. сформировать соответствующее нечеткое множество Пример: Рассмотрим лингвистическую переменную с именем "температура в комнате". Тогда оставшуюся четверку 1) универсальное множество ; 2) терм-множество T={"холодно", "комфортно", "жарко"} с такими функциями принадлежностями:    3) синтаксические правила , порождающее новые термы с использованием квантификаторов "и","или", "не", "очень","более-менее" и других; 4) М будет являться процедурой, ставящей каждому новому терму в соответствие нечёткое множество из Х по правилам: если термы А и В имели функции принадлежности μА(u) и μB(u) соответственно, то новые термы будут иметь следующие функции принадлежности, заданные в таблице:
Четкая переменнаяОпр: Чёткая переменная может быть определена как совокупность <α, X, A>, где: α - наименование переменной, X - универсальное множество (область определения α ), A - четкое множество на X, определяющее область значений переменной. Пример: x-наименование переменной, X=R, А=[0,100]. ]100,0[∈x Нечеткая переменнаяОпр: Нечеткая переменная характеризуется тройкой <α, X, A>, где α - наименование переменной, X - универсальное множество (область определения α), A – функция принадлежности μ(x) определённая на X, говорящая о степени уверенности в том, что х является значением нечёткой переменной. Пример: Нечеткая переменная «старый», где старый - наименование переменной, Х=[0,100], А - нечёткое множество, определяемое линейной функцией Нечеткое множество (fuzzy set)Понятие нечеткого множества - попытка математической формализации нечеткой информации для построения математических моделей. В основе этого понятия лежит представление о том, что составляющие данное множество элементы, обладающие общим свойством, могут обладать этим свойством в различной степени и, следовательно, принадлежать к данному множеству с различной степенью. При таком подходе высказывания типа “такой-то элемент принадлежит данному множеству” теряют смысл, поскольку необходимо указать “насколько сильно” или с какой степенью конкретный элемент удовлетворяет свойствам данного множества. Основным положением теории нечетких множеств является расширение классического понятия множества. В случае классического канторовского множества, о любом элементе из глобального множества можно сказать только то, что оно принадлежит или не принадлежит данному множеству. То есть характеристическая функция множества (функция, определяющая принадлежность некоторого элемента глобального множества данному множеству) принимает значения 0 либо 1. В случае расширенного понятия множества функция принадлежности может принимать любые значения из отрезка [0,1] – такое множество Л. Заде назвал нечетким множеством (fuzzy set). Таким образом, нечеткое множество А представляет собой множество упорядоченных пар вида (μ, х), где 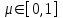 , а , а 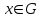 , где G – глобальное множество элементов или , где G – глобальное множество элементов илиА = {(μ, х): 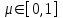 , , 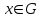 } }Характеристическая функция F определяет отображение элементов глобального множества на отрезок [0,1] действительной оси: F: G → [0,1]. Функцию принадлежности нечеткого множества (характеристическая функция) можно задать несколькими способами. Первый способ табличный – для каждого элемента глобального множества задается значение функции принадлежности элемента данному нечеткому множеству. Второй способ – графическое задание функции принадлежности. Вообще говоря, функция принадлежности может иметь любой вид, однако сейчас сформировалось понятие о так называемых стандартных функциях: Z- функция, S- функция, П - функция, Л – функция (Рис.). 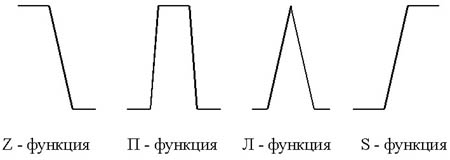 Для задания любой физической величины или понятия, существенного для описания системы, в нечеткой логике используется лингвистическая переменная. Лингвистическая переменная обычно обозначается словом или фразой на естественном языке, например, “скорость”, “красота”, “надежность”. Значение, которое может принимать лингвистическая переменная, называется термом. Терм также обозначается словом или группой слов, которые характеризуют различные состояния системы относительно понятия, определяемого лингвистической переменной. Например, “надежность” может быть “высокой”, “средней”, “низкой”. Каждому терму лингвистической переменной соответствует нечеткое множество, что позволяет говорить о степени принадлежности каждого элемента глобального множества данному терму. Например, значение скорости 10 км/ч для лингвистической переменной “скорость” относится к терму “высокая” со степенью принадлежности 0.1, а к терму “низкая” со степенью 0.9. Это отражает тот факт, что скорость 10 км/ч скорее можно назвать низкой скоростью, чем высокой. Для представления знаний, правил, по которым функционирует система, в теории нечеткой логики используются продукционные правила. Каждое продукционное правило состоит из одной или нескольких посылок и заключения. В случае нескольких посылок они соединяются связками “И” и “ИЛИ”. Левая часть правила, в которой находятся условия, носит название антецедент. Правая часть, в которой содержится результат, называется консеквент. Лингвистическую переменную, входящую в консеквент, будем называть выходной переменной. Лингвистическую переменную, которой соответствует параметр системы, для которого необходимо выработать управляющее воздействие, будем называть выводимой переменной, а сам параметр выходным параметром. Все лингвистические переменные, соответствующие параметрам, на основе которых вычисляется состояние системы в следующий момент времени, будем называть входными переменными, а такие параметры – входными параметрами. Посылка и заключение сходны по своей структуре и содержат лингвистическую переменную и принимаемое переменной значение – терм. Пример: ЕСЛИ (“Известность столицы” = “Популярна”) ТО (“Отпуск” = “Хороший”). Для того чтобы реализовать необходимое управление системой необходимо уметь преобразовывать имеющиеся текущие сведения о системе и внешних факторах в точное управляющее воздействие, поскольку механизм, вырабатывающий воздействие требует указания точного численного значения, которое должно быть приложено к системе. Например, системе рулевого управления самолетом нельзя давать указания в виде “повернуть руль немного левее” – система управления потребует указания точного числа градусов, на которое нужно повернуть руль. Для этого необходимо имеющиеся точные значения входных параметров (например, отклонение от заданной траектории полета, текущий крен самолета и т.п.) преобразовать к нечетким лингвистическим переменным, затем на основе имеющихся правил сделать соответствующие заключения для выходных переменных, далее необходимо объединить результаты выводов для выводимой переменной и получить четкое значение для выработки управляющего воздействия. Этот процесс получения четкого значения для управляющего воздействия называют процессом нечеткого вывода. Основные операции над нечеткими множествами Основные операции над четкими множествами: Пересечение множеств ; BACI=Объединение множеств C = A U B ; Отрицание (дополнение) множества АC=. Заде предложил набор аналогичных операций над НМ через операции с функциями принадлежности: Если А <=> μА(u), В <=> μВ(u), то результат операций - нечеткое множество С <=> μС(u), причем: если С = А ∩ В, то μС(u) = min(μА(u), μВ(u)); если С = А ∪ В, то μС(u) = max(μА(u), μВ(u)); если С = A, то μС(u) = 1 - μА(u). Нечеткий выводНечетким логическим выводом(fuzzy logic inference) называется аппроксимация зависимости Y = f(X1,X2…Xn) каждой выходной лингвистической переменной от входных лингвистических переменных и получение заключения в виде нечеткого множества, соответствующего текущим значениях входов, с использованием нечеткой базы знаний и нечетких операций. Основу нечеткого логического вывода составляет композиционное правило Заде. В общем случае нечеткий вывод решения происходит за три (или четыре) шага: 1) Этап фаззификации. С помощью функций принадлежности всех термов входных лингвистических переменных и на основании задаваемых четких значений из универсов входных лингвистических переменных определяются степени уверенности в том, что выходная лингвистическая переменная принимает значение – конкретный терм. Эта степень уверенности есть ордината точки пересечения графика функции принадлежности терма и прямой x = четкое значение ЛП. 2) Этап непосредственного нечеткого вывода. На основании набора правил – нечеткой базы знаний – вычисляется значение истинности для предпосылки каждого правила на основании конкретных нечетких операций, соответствующих конъюнкции или дизъюнкции термов в левой части правил. В большинстве случаев это либо максимум, либо минимум из степеней уверенности термов, вычисленных на этапе фаззификации. которое применяется к заключению каждого правила. Используя один из способов построения нечёткой импликации мы получим нечёткую нечеткую переменную, соответствующую вычисленному значению степени уверенности в левой части правила и нечеткому множеству в правой части правила. Обычно в качестве для вывода используется минимизация или правила продукции. При минимизирующем логическом выводе, выходная функция принадлежности ограничена сверху в соответствии с вычисленной степенью истинности посылки правила(нечеткое логическое И). В логическом выводе с использованием продукций, выходная функция принадлежности масштабируется с помощью вычисленной степенью истинности предпосылки правила. 3) Этап композиции (агрегации, аккумуляции). Все нечеткие множества, назначенные для каждого терма каждой выходной лингвистической переменной объединяются вместе и формируется единственное нечеткое множество - значение для каждой выводимой лингвистической переменной. Наконец снова, обычно используются функции MAX или SUM. 4) Этап дефаззификации. (необязательный). Используется тогда, когда полезно преобразовывать нечеткий набор значений выводимых лингвистических переменных к точным значениям. Имеется достаточно большое количество методов перехода к точным значениям (по крайней мере 30). Два из общих методов - это «методы полной интерпретации» и «по максимуму». В методе полной интерпретации, точное значение выводимой переменной вычисляется как значение "центра тяжести" функции принадлежности для нечеткого значения. В методе максимума в качестве точного значения выводимой переменной принимается максимальное значение функции принадлежности. В теории нечетких множеств процедура дефаззификации аналогична нахождения характеристик положения (математического ожидания, моды, медианы) случайных величин в теории вероятности. Простейшим способом выполнения процедуры дефаззификации является выбор четкого числа, соответствующего максимуму функции принадлежности. Однако пригодность этого способа ограничивается лишь одноэкстремальными функциями принадлежности. Для многоэкстремальных функций принадлежности часто используются следующие методы дефаззификации: 1) COG (center of gravity) – «центр тяжести». Физическим аналогом этой формулы является нахождение центра тяжести плоской фигуры, ограниченной осями координат и графиком функции принадлежности нечеткого множества. 2) MOM (mean of maximums) - центр максимумов. В методе центра максимумов находится среднее арифметическое элементов универсального множества, имеющих максимальные степени принадлежностей. 3) First Maximum («первый максимум»). Это максимум функции принадлежности с наименьшей абсциссой. Функциональная схема процесса нечеткого вывода в упрощенном виде представлена на рисунке. На этой схеме выполнение первого этапа нечеткого вывода – фаззификации – осуществляет фаззификатор. За процедуру непосредственно нечеткого вывода ответственна машина нечеткого логического вывода, которая производит второй этап процесса вывода на основании задаваемой нечеткой базы знаний (набора правил), и этап композиции. Дефаззификатор производит последний этап нечеткого вывода – дефаззификацию. 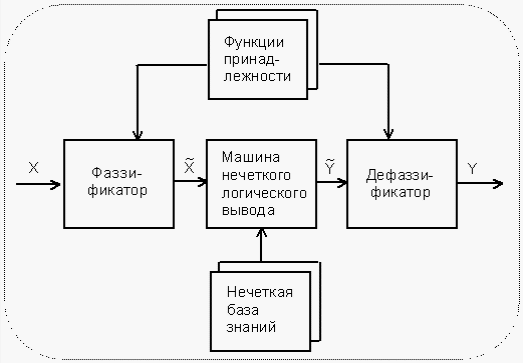 Нечеткий логический вывод Рассмотрим алгоритм нечеткого вывода на конкретном примере: работы автопилота при движении автомобиля по дороге. Рассмотрим процесс нечеткого вывода на примере движения автомобиля по дороге. Будем считать, что маршрут движения автомобиля задан, и необходимо выработать управляющее воздействие на скорость автомобиля, для того, чтобы не врезаться в движущийся впереди автотранспорт, одновременно с этим необходимо как можно скорее добраться до конечной точки назначения. Для описанной ситуации параметром, влияющим на состояние системы (скорость автомобиля), очевидно, является дистанция до находящегося впереди препятствия. Поскольку необходимо выработать управляющее воздействие на скорость автомобиля то выводимой переменной является лингвистическая переменная СКОРОСТЬ. Параметр, влияющий на состояние системы – это расстояние до препятствия, которому поставим в соответствие лингвистическую переменную ДИСТАНЦИЯ. Определим значения, которые могут принимать лингвистические переменные так, как показано на Рис  Зададимся тремя правилами, регулирующими понятие скорости: ЕСЛИ (ДИСТАНЦИЯ = ДАЛЕКО) ТО (СКОРОСТЬ = ВЫСОКАЯ) ЕСЛИ (ДИСТАНЦИЯ= СРЕДНЕ) ТО (СКОРОСТЬ = СРЕДНЯЯ) ЕСЛИ (ДИСТАНЦИЯ = БЛИЗКО) ТО (СКОРОСТЬ = НИЗКАЯ) Процесс фаззификации заключается в том, чтобы все имеющиеся точные значения входных параметров преобразовать к значениям соответствующих лингвистических переменных. Дословно фаззификация означает переход к нечеткости. В нашем случае входным параметром является дистанция до препятствия. Предположим, что значение дистанции равно 25 метров. Для каждого значения терма переменной ДИСТАНЦИЯ по имеющимся функциям принадлежности вычислим степень принадлежности значения 25 метров. Для термов БЛИЗКО, СРЕДНЕ, ДАЛЕКО значения функции принадлежности равны соответственно 0, 1, 1/6. Таким образом, четкое значение 25 метров преобразовано к нечетким значениям БЛИЗКО, СРЕДНЕ, ДАЛЕКО. Второй этап нечеткого вывода состоит в логическом выводе выводимой переменной посредством построения цепочки правил, у которой в левой части первого правила находятся входные переменные, а в правой части последнего правила цепочки находится выводимая переменная. Промежуточные правила цепочки строятся таким образом, что в антецеденте промежуточного правила находится переменная, стоящая в консеквенте предшествующего правила. В нашем случае имеется 3 цепочки, обеспечивающие вывод для выводимой переменной. Цепочки состоят из одного правила. В левой части каждого правила находится входная переменная – ДИСТАНЦИЯ, а в правой части – выводимая переменная СКОРОСТЬ Цель логического вывода (второго этапа нечеткого вывода) – получить степень принадлежности параметра системы, для которого формируется управляющее воздействие, к соответствующей лингвистической переменной. Если в антецеденте параметр системы принадлежит соответствующей лингвистической переменной со степенью принадлежности μ, то полагают, что параметр системы, соответствующий лингвистической переменной консеквента этого правила, также имеет степень принадлежности μ. Каждое из правил представляет из себя нечёткую импликацию. Степень уверенности посылки мы вычислили, а степень уверенности заключения задаётся функцией принадлежности соответствующего терма. Поэтому используя один из способов построения нечёткой импликации мы получим новую нечёткую переменную, соответствующую степени уверенности о значении выходного значения при применении к заданным входным соответствующего правила. Используя определение нечёткой импликации как минимума левой и правой частей, имеем: Предположим, что найдена цепочка правил вида (ЕСЛИ А0=а0 ТО A1 = a1 ) → (ЕСЛИ А1=а1 ТО A2 = a2) → … → (ЕСЛИ Аn-1=аn-1 ТО An =an), где А0 – лингвистическая переменная, соответствующая входному параметру, Аn – переменная, соответствующая выводимой переменной, аi – терм лингвистической переменной, а Pi – параметр системы, соответствующий лингвистической переменной Ai. Если P0 принадлежит А0 со степенью принадлежности μ , то тогда параметр P1 принадлежит А1 со степенью принадлежности μ, а из второго правила цепочки следует, что P2 принадлежит А2 со степенью принадлежности μ и т.д. Получается, что Pn принадлежит Аn со степенью принадлежности μ. Если антецедент правила состоит из нескольких посылок, то в случае связки ИЛИ выбирается максимальная степень принадлежности, в случае связки И – минимальная. В результате выполнения логического вывода имеем все возможные цепочки, из которых можно вывести выводимую переменную, каждой из которых соответствует некоторая степень принадлежности выходного параметра выводимой переменной . Третий этап нечеткого вывода – композиция. На этом этапе из полученных цепочек логических выводов необходимо выработать единое значение степени принадлежности выходного параметра к выводимой переменной.  Для этого можно сгруппировать найденные цепочки по значению терма выводимой переменной в последнем правиле цепочки. Для каждой группы можно найти среднее значение степени принадлежности управляющего воздействия к выводимой переменной. В нашем случае у выводимой переменной существует 3 терма, поэтому все цепочки разбиваются на 3 группы – по одной цепочке в одной группе. То есть управляющее воздействие – скорость – принадлежит терму НИЗКАЯ со степенью принадлежности 0, СРЕДНЯЯ – со степенью 1, ВЫСОКАЯ – со степенью 1/6. Для этого можно сгруппировать найденные цепочки по значению терма выводимой переменной в последнем правиле цепочки. Для каждой группы можно найти среднее значение степени принадлежности управляющего воздействия к выводимой переменной. В нашем случае у выводимой переменной существует 3 терма, поэтому все цепочки разбиваются на 3 группы – по одной цепочке в одной группе. То есть управляющее воздействие – скорость – принадлежит терму НИЗКАЯ со степенью принадлежности 0, СРЕДНЯЯ – со степенью 1, ВЫСОКАЯ – со степенью 1/6.П 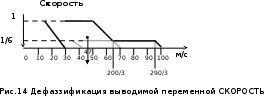 оследний этап нечеткого вывода – дефаззификация, то есть переход к четкости. Имея значения степени принадлежности выходного параметра к термам выводимой переменной, можно рассчитать четкое значение. оследний этап нечеткого вывода – дефаззификация, то есть переход к четкости. Имея значения степени принадлежности выходного параметра к термам выводимой переменной, можно рассчитать четкое значение.Одним из способов осуществить дефаззификацию является метод центроида. Необходимо найти центр массы фигуры, построенной как объединение фигур полученных от каждого терма выводимой переменной. Фигура терма ограничивается графиком функции принадлежности и линией уровня, определяющего степень принадлежности выходного параметра выводимой переменной. Семантическая сеть Семантическая сеть, этот метод представления знаний позволяет описывать объекты, явления и понятия предметной области с помощью теории графов Семантическая сеть представляет собой ориентированный граф, где узлы представляют понятия предметной области, а связи – отношения между понятиями. В качестве понятий обычно выступают абстрактные или конкретные объекты, концепты или события, а отношения – это связи следующих видов: 1. связи, определяющие тип объектов ("это есть" или "класс- подкласс", "иметь частью" или "часть-целое", "принадлежать" или "элемент-множество" и т.п.); 2. функциональные связи (определяемые обычно глаголами "производит", "влияет" …); 3. количественные ("больше", "меньше", "равно" …); 4. пространственные ("далеко от", "близко от", "за", "под", "над" ...); 5. временные ("раньше", "позже", "в течение" …); 6. атрибутивные связи (иметь свойство, иметь значение...); 7. логические связи ("и", "или", "не") и др. Характерной особенностью семантических сетей является обязательное наличие в одной сети трех типов отношений: _ класс - элемент класса; _ свойство - значение; _ экземпляр элемента класса. Поиск решения в базе знаний типа семантической сети сводится к задаче поиска фрагмента сети, соответствующего некоторой подсети, отвечающей поставленному вопросу используя методы теории графов. ЗАО1 поставило Клиенту1 Компьютер1 с требуемыми характеристиками. Клиент1 находится в Санкт-Петербурге, а ЗАО1 в Москве. Отобразим отношения между сущностями с помощью семантической сети. 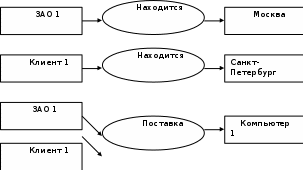 Построения семантической сети Для построения СС необходимо выполнить следующие шаги: 1. Определить абстрактные объекты и понятия предметной области, необходимые для решения поставленной задачи. Оформить их в виде вершин. Задать свойства для выделенных вершин, оформив их в виде вершин, связанных с исходными вершинами атрибутивными отношениями. Задать связи между вершинами, используя функциональные, пространственные, количественные, логические, временные, атрибутивные отношения, а также отношения типа «являться наследником» (АКО) и «являться частью» (ISA). 4. Добавить конкретные объекты и понятия, описывающие решаемую задачу. Оформить их в виде вершин, связанных с уже существующими отношениями типа «являться экземпляром», «есть». 5. Проверить правильность установленных отношений (вершины и отношения при правильном построении образуют предложение). Пример. Построить сетевую модель представления знаний в предметной области «Автозаправка» (посещение автозаправки). Решение. 1. Ключевые понятия данной предметной области - автозаправка, тот, кто посещает автозаправку (клиент), и те, кто его обслуживают (заправщики). У обслуживающего персонала и клиентов есть общие характеристики, поэтому целесообразно выделить общее абстрактное понятие - человек. Продукцией автозаправки является топливо. Исходя из этого, вершинами графа будут: «Автозаправка», «Человек», «Заправщик», «Клиент», «Заказ» и «Топливо». У этих объектов есть определенные свойства и атрибуты. Например, автозаправки располагаются по определенным адресам, топливо имеет цену. Поэтому добавим в граф вершины «Адрес» и «Цена». Определим для имеющихся вершин графа отношения и их типы. Добавим знание о конкретных фактах решаемой задачи. Пусть имеются две автозаправки: «Лукойл» и «Кобарт». На автозаправке «Лукойл» работает заправщик Иван, на автозаправке «Кобарт» - Федор Полученный в результате граф Для получения ответа на какой-либо вопрос по этой задаче, необходимо найти соответствующий участок сети и, используя отношения, получить результат. 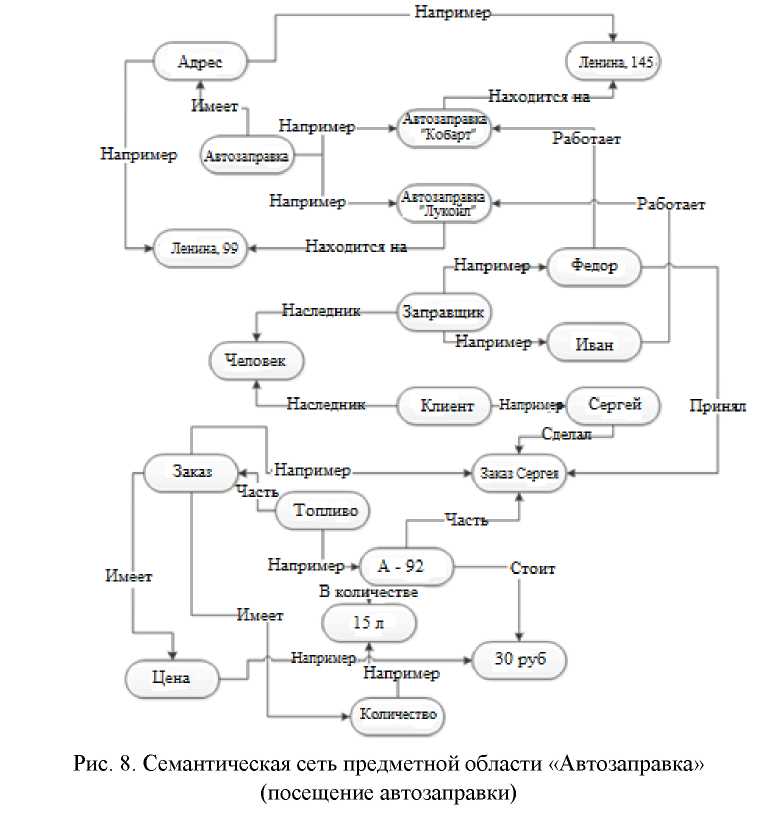 |
